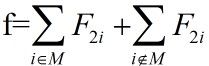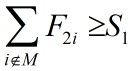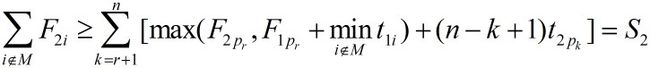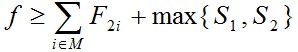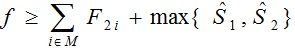0040算法笔记——【分支限界法】批处理作业调度问题

      问题描述

     给定n个作业的集合{J1,J2,…,Jn}。每个作业必须先由机器1处理，然后由机器2处理。作业Ji需要机器j的处理时间为tji。对于一个确定的作业调度，设Fji是作业i在机器j上完成处理的时间。所有作业在机器2上完成处理的时间和称为该作业调度的完成时间和。

     批处理作业调度问题要求对于给定的n个作业，制定最佳作业调度方案，使其完成时间和达到最小。

      例：设n=3，考虑以下实例：

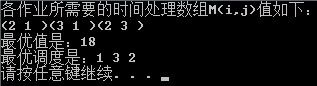
     这3个作业的6种可能的调度方案是1,2,3；1,3,2；2,1,3；2,3,1；3,1,2；3,2,1；它们所相应的完成时间和分别是19，18，20，21，19，19。易见，最佳调度方案是1,3,2，其完成时间和为18。

     限界函数

     批处理作业调度问题要从n个作业的所有排列中找出具有最小完成时间和的作业调度，所以如图，批处理作业调度问题的解空间是一颗排列树。     

     在作业调度问相应的排列空间树中，每一个节点E都对应于一个已安排的作业集。以该节点为根的子树中所含叶节点的完成时间和可表示为：

     设|M|=r，且L是以节点E为根的子树中的叶节点，相应的作业调度为{pk,k=1,2,……n}，其中pk是第k个安排的作业。如果从节点E到叶节点L的路上，每一个作业pk在机器1上完成处理后都能立即在机器2上开始处理，即从pr+1开始，机器1没有空闲时间，则对于该叶节点L有：

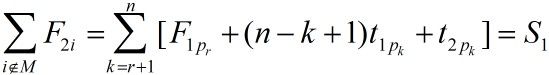注：(n-k+1)t1pk,因为是完成时间和，所以，后续的(n-k+1)个作业完成时间和都得算上t1pk。

     如果不能做到上面这一点，则s1只会增加，从而有：。

     类似地，如果从节点E开始到节点L的路上，从作业pr+1开始，机器2没有空闲时间，则：

     同理可知，s2是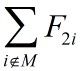的下界。由此得到在节点E处相应子树中叶节点完成时间和的下界是：

     注意到如果选择Pk，使t1pk在k>=r+1时依非减序排列，S1则取得极小值。同理如果选择Pk使t2pk依非减序排列，则S2取得极小值。 

     这可以作为优先队列式分支限界法中的限界函数。 

     算法描述

      算法中用最小堆表示活节点优先队列。最小堆中元素类型是MinHeapNode。每一个MinHeapNode类型的节点包含域x,用来表示节点所相应的作业调度。s表示该作业已安排的作业时x[1:s]。f1表示当前已安排的作业在机器1上的最后完成时间；f2表示当前已安排作业在机器2上的完成时间；sf2表示当前已安排的作业在机器2上的完成时间和；bb表示当前完成时间和下界。二维数组M表示所给的n个作业在机器1和机器2所需的处理时间。在类Flowshop中用二维数组b存储排好序的作业处理时间。数组a表示数组M和b的对应关系。算法Sort实现对各作业在机器1和2上所需时间排序。函数Bound用于计算完成时间和下界。

     函数BBFlow中while循环完成对排列树内部结点的有序扩展。在while循环体内算法依次从活结点优先队列中取出具有最小bb值（完成时间和下界）的结点作为当前扩展结点，并加以扩展。 算法将当前扩展节点E分两种情形处理：

　1)首先考虑E.s=n的情形，当前扩展结点E是排列树中的叶结点。E.sf2是相应于该叶结点的完成时间和。当E.sf2 < bestc时更新当前最优值bestc和相应的当前最优解bestx。 

    2)当E.s

    算法具体实现如下：

     1、MinHeap2.h

#include 

template
class Graph;

template 
class MinHeap 
{ 
	template
	friend class Graph;
	public: 
		MinHeap(int maxheapsize = 10); 
		~MinHeap(){delete []heap;} 

		int Size() const{return currentsize;} 
		T Max(){if(currentsize) return heap[1];} 

		MinHeap& Insert(const T& x); 
		MinHeap& DeleteMin(T &x); 

		void Initialize(T x[], int size, int ArraySize); 
		void Deactivate(); 
		void output(T a[],int n);
	private: 
		int currentsize, maxsize; 
		T *heap; 
}; 

template  
void MinHeap::output(T a[],int n) 
{ 
	for(int i = 1; i <= n; i++) 
	cout << a[i] << " "; 
	cout << endl; 
} 

template  
MinHeap::MinHeap(int maxheapsize) 
{ 
	maxsize = maxheapsize; 
	heap = new T[maxsize + 1]; 
	currentsize = 0; 
} 

template 
MinHeap& MinHeap::Insert(const T& x) 
{ 
	if(currentsize == maxsize) 
	{ 
		return *this; 
	} 
	int i = ++currentsize; 
	while(i != 1 && x < heap[i/2]) 
	{ 
		heap[i] = heap[i/2]; 
		i /= 2; 
	} 

	heap[i] = x; 
	return *this; 
} 

template 
MinHeap& MinHeap::DeleteMin(T& x) 
{ 
	if(currentsize == 0) 
	{ 
		cout<<"Empty heap!"< heap[ci + 1]) 
		{ 
			ci++; 
		} 

		if(y <= heap[ci]) 
		{ 
			break; 
		} 
		heap[i] = heap[ci]; 
		i = ci; 
		ci *= 2; 
	} 

	heap[i] = y; 
	return *this; 
} 

template 
void MinHeap::Initialize(T x[], int size, int ArraySize) 
{ 
	delete []heap; 
	heap = x; 
	currentsize = size; 
	maxsize = ArraySize; 

	for(int i = currentsize / 2; i >= 1; i--) 
	{ 
		T y = heap[i]; 
		int c = 2 * i; 
		while(c <= currentsize) 
		{ 
			if(c < currentsize && heap[c] > heap[c + 1]) 
				c++; 
			if(y <= heap[c]) 
				break; 
			heap[c / 2] = heap[c]; 
			c *= 2; 
		} 
		heap[c / 2] = y; 
	} 
} 

template 
void MinHeap::Deactivate() 
{ 
	heap = 0; 
} 

    2、6d9.cpp

//批作业调度问题 优先队列分支限界法求解 
#include "stdafx.h"
#include "MinHeap2.h"
#include 
using namespace std;

class Flowshop;
class MinHeapNode
{
	friend Flowshop;
	public:
		operator int() const
		{
			return bb;
		}
	private:	
		void Init(int);
		void NewNode(MinHeapNode,int,int,int,int);
		int s,			//已安排作业数
			f1,			//机器1上最后完成时间
			f2,			//机器2上最后完成时间
			sf2,		//当前机器2上完成时间和
			bb,			//当前完成时间和下界
			*x;			//当前作业调度
};

class Flowshop
{
	friend int main(void);
	public:
		int BBFlow(void);
	private:
		int Bound(MinHeapNode E,int &f1,int &f2,bool **y);
		void Sort(void);
		int n,			//作业数
			** M,		//各作业所需的处理时间数组
			**b,		//各作业所需的处理时间排序数组
			**a,		//数组M和b的对应关系数组
			*bestx,		//最优解
			bestc;		//最小完成时间和
		bool **y;		//工作数组
};

template 
inline void Swap(Type &a, Type &b);

int main()
{
	int n=3,bf;
	int M1[3][2]={{2,1},{3,1},{2,3}};

	int **M = new int*[n];
	int **b = new int*[n];
	int **a = new int*[n];
	bool **y = new bool*[n];
	int *bestx = new int[n];  

    for(int i=0;i<=n;i++)
	{
        M[i] = new int[2];
		b[i] = new int[2];
		a[i] = new int[2];
		y[i] = new bool[2];
	}
	cout<<"各作业所需要的时间处理数组M(i,j)值如下："<i; k--)
			{
				if(b[k][j]E.f2)?f1:E.f2)+M[E.x[E.s]][1];
	int sf2 = E.sf2 + f2;
	int s1 = 0,s2 = 0,k1 = n-E.s,k2 = n-E.s,f3 = f2;

	//计算s1的值
	for(int j=0; jf1+b[j][0])?f2:f1+b[j][0];
			}
			s1 += f1+k1*b[j][0];
		}
	}

	//计算s2的值
	for(int j=0; js2)?s1:s2);
}

//解批处理作业调度问题的优先队列式分支限界法
int Flowshop::BBFlow(void)
{
	Sort();//对各作业在机器1和2上所需时间排序
	MinHeap H(1000);

	MinHeapNode E;
	//初始化
	E.Init(n);
	//搜索排列空间树
	while(E.s<=n)
	{
		//叶节点
		if(E.s == n)
		{
			if(E.sf2
inline void Swap(Type &a, Type &b)
{ 
	Type temp=a; 
	a=b; 
	b=temp;
}

     程序运行结果如图：