阵列信号DOA估计系列(一).概述

1.从相位差说起

大家都知道，对于一个正弦信号$y=sin(2\pi f_{0}t)$，以采样间隔$T_s$进行连续、均匀采样，假设采样$N$点的数据，那么这些数据点写下来应该是$$y(n)=[sin(2\pi f_0\times 0),sin(2\pi f_0\times T_s),sin(2\pi f_0\times 2T_s),\cdots ,sin(2\pi f_0\times (N-1)T_s)]$$将其相位写下来，应该是$$Phase[y(n)]=[0,2\pi f_0\times T_s,2\pi f_0\times 2T_s,\cdots ,2\pi f_0\times (N-1)T_s]$$从信号与系统我们可以知道，对离散信号做傅里叶变换（ MATLAB中用 fft ），可以提取信号中的频率参数，即$f_0$。

以上都是我们熟知的东西，那么这个地方就可以引入一个思考：假设给我们一串离散信号$y(n)$，信号的采样点之间相位差是均匀排列的，FFT搞一遍，就可以得到频率信息了！此时，我们并不知道$y(n)$中数据点的来源，也许不是上面说的时序均匀采样而得，但是这并不妨碍我们FFT一顿操作猛如虎，一看频率250（哈哈

2.空间相位差的来源

相位差大家都懂，为何要强调空间相位差？其实这是一个习惯的问题，为的是表达相位差异的直接来源是“空间”，而不是时间。

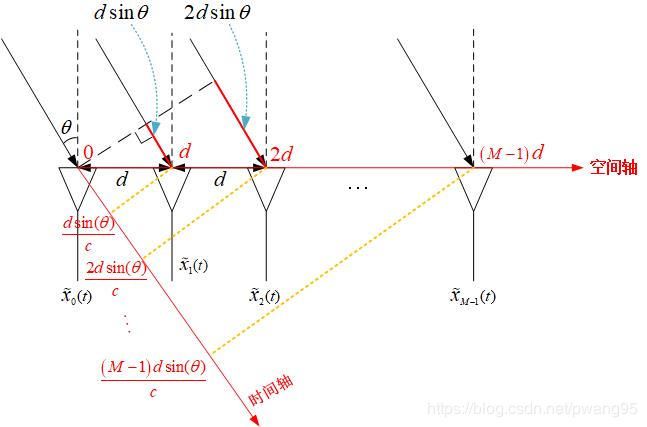
看下面这样一个例子：均匀线性阵列，共有 $M$ 个阵元，阵元之间相距 $d$，有一个信号（假设为平面波）从偏离法线 $\theta$ 方向射入到阵列上。

可以看出，信号要到达第二个阵元所走过的路程 比 到达第一个阵元走过的路程 要多 $dsin(\theta )$ ,后面以此类推，信号要到达后面一个阵元 都比 前面一个阵元 多走 $dsin(\theta )$ 的空间距离。

我们都知道电磁波的速度为光速$c$,那么上面的路程计算到时间维度，可以得出：相同的信号，要到达后一个阵元，就比前一个阵元 在时间上 迟了 $\delta t=\frac{dsin(\theta )}{c}$。假设信号的频率为$f_0$，并且以第一个阵元为参考点，那么每一个阵元相对于第一个阵元的时间差为$$\Delta t=[0,\frac{dsin(\theta )}{c},\frac{2dsin(\theta )}{c},\cdots ,\frac{(M-1)dsin(\theta )}{c}]$$
那么到达各个阵元的信号，相对于第一个阵元的相位差就应该是$$\Delta \varphi =[0,2\pi f_0\frac{dsin(\theta )}{c},2\pi f_0\frac{2dsin(\theta )}{c},\cdots ,2\pi f_0\frac{(M-1)dsin(\theta )}{c}]$$由于这个相位差是阵元间空间位置不同所造成的，顺便取了个名字为“空间相位差”。

另外，可以从这个图的角度去理解。

3.从“空间相位差”到“DOA估计”

首先还是再仔细观察一下在时域和频域，我们常用的FFT的一些细节。

3.1 时域

在时域里面，将离散时间信号$$y(n)=[sin(2\pi f_0\times 0),sin(2\pi f_0\times T_s),sin(2\pi f_0\times 2T_s),\cdots ,sin(2\pi f_0\times (N-1)T_s)]$$做FFT，可以提取出数字频率$$\omega =2\pi f_0{T}_s=2\pi \frac{f_0}{f_s}$$仔细观察可以看出，这个数字频率，就是相邻采样点之间相位差 $\delta \varphi =2\pi f_0{T}_s=2\pi \frac{f_0}{f_s}$。 如果画出频谱图，那么将会在 $2\pi \frac{f_0}{f_s}$ 处出现一个峰值。
这基本就是我们在时域使用FFT对估计信号频率的简单理解了。

3.2 空域

对应到空域里面，在某一时刻对所有每个阵元同时采样（称之为一个快拍），将会得到 $M$ 个数据点，将这 $M$ 个数据点排列起来，可以得到$$\mathbf{x}(n)=[s(t),s(t)e^{j2\pi f_0\frac{dsin(\theta )}{c}},s(t)e^{j2\pi f_0\frac{2dsin(\theta )}{c}},s(t)e^{j2\pi f_0\frac{3dsin(\theta )}{c}},\cdots ,s(t)e^{j2\pi f_0\frac{(M-1)dsin(\theta )}{c}}]$$如果对这一串数据做FFT，那么将会得到相邻数据点的相位差 $$\delta \varphi =2\pi f_0\frac{dsin(\theta )}{c}=2\pi \frac{dsin(\theta )}{\lambda }$$与时域类比，可以知道，这应该是一个数字频率。同样，若画出频谱图，那么应该在 $2\pi \frac{dsin(\theta )}{\lambda }$处有一个峰值，再通过一定的运算（反正弦等），就可以提取出角度 $\theta$ 的的信息了。这就是空域FFT的直观理解。

3.3 DOA估计

对于均匀线阵，某一时刻接收到一个快拍信号$$\mathbf{x}(n)=[x_0(n),x_1(n),x_2(n),\cdots ,x_{M-1}(n)]$$，就可以直接用FFT操作，就可以得到角度信息了。当然，这里面有很多的问题，下面马上就会讲到。

4. 一些问题和思考

本篇博文所讲，是DOA估计最最基本的概念问题，相当于DOA 估计领域的"hello world！"。有一些不严谨、或者说不专业的地方，下面略微提一下。以后有时间，我再慢慢填坑。

1. 通过这种和时域比较的方法来理解，对于新手来说是比较友好的。但是，我觉得这是不严谨的。作为一个工科生，我只相信数据和推导，这才是专业选手的做法。上面所说，对均匀线阵的一个快拍数据做FFT可以得到一个峰值，是通过类比的方式得出的。其实，也可以通过严格的数学计算证明的。
2. 上面只说了一个快拍，万一信噪比不够呢？如何利用多个快拍？
3. 本文一直在拿时间和空间做类比，那么这两者的关系到底是什么？

ps：若有错误，希望大家提出。如有建议，欢迎大家讨论。