每天一篇论文 369/1000 D3VO: Deep Depth, Deep Pose and Deep Uncertainty for Monocular Visual Odometry

D3VO: Deep Depth, Deep Pose and Deep Uncertainty for Monocular Visual Odometry

论文阅读汇总list

摘要

我们提出D3VO作为一种新的单目视觉测程框架，它利用了深度、姿态和不确定度三个层次上的深度网络。首先，我们提出了一种基于双目视频的自监督单目深度估计网络。特别地，它利用预测亮度变换参数将训练图像对对齐到相似的光照条件。此外，我们对输入图像上像素的光度不确定性进行了建模，提高了深度估计的精度，并为直(无特征)视觉测程法中的光度残值提供了一个学习加权函数。评价结果表明，该网络的性能优于现有的自监督深度估计网络。D3VO将预测的深度、姿态和不确定性紧密地结合到一个直接的视觉测程方法中，以促进前端跟踪和后端非线性优化。我们在KITTI测程基准和EuRoC MAV数据集上用单目视觉测程来评估D3VO。结果表明，D3VO法明显优于传统单目VO法。它还实现了与最先进的立体声/激光雷达测程的KITTI和最先进的视觉惯性测程的EuRoC MAV，而只使用一个摄像头。

方法

我们首先介绍了一种新的自监督神经网络，它可以预测深度、姿态和不确定性。该网络还估计仿射亮度变换参数，以自监督的方式对齐训练图像的照明。光度不确定度是根据每个像素可能的亮度值的分布来预测的。然后，我们介绍了D3VO作为一个直接的视觉测程框架，将预测的性能纳入到跟踪前端和光度束调整后端。

1.自监督深度估计
自我监督训练是通过最小化时间和静态立体图像之间的光度重投影误差来实现的:
$$L_{slef}=\frac{1}{|V|}\sum _{p\in v}\underset{t^{\prime }}{\min }r(I_t,I_{t^{\prime }\to t})$$
其中$V$ 是图像$I_t$上所有像素集合，$t^{\prime }$是所有原图的索引。

传统的深度估计几何偏差为：
$$r(I_a,I_b)=\frac{\alpha }{2}(1-SSIM(I_a,I_b))+(1-\alpha )||I_a-I_b||$$
以上公式是基于光度恒定假设。然而，**由于相机的光照变化和自动曝光影响，L1和SSIM都不是固定不变的，因此可能会违反以上假设。**因此，我们建议使用预测亮度转换参数来明确地建模相机曝光变化。这也是本文的出发的核心

2.亮度转移参数

图1 在EuRoC MAV上相似亮度变换的实例。原始的源图像$I_{t^{\prime }}$和目标图像$I_t$显示不同的亮度。在预测参数a、b的情况下，变换后的目标图像$I_t^{a_{r^{\prime }}{b}_{r^{\prime }}}$与源图像具有相似的亮度，有利于基于亮度恒常性假设的自监督训练。

相机曝光调整引起的图像强度变化可以用a、b两个参数的映射变换来表示：
$$I^{a,b}=aI+b$$
尽管它很简单，这个公式已经被证明在直接VO/SLAM中是有效。受一些恒定光度工作的启发，通过预测变换参数a, b,使预测图像$I_{t^{\prime }}$与$I_t$ 的亮度条件一致。公式(1)重新表述为：
$$L_{slef}=\frac{1}{|V|}\sum _{p\in V}\underset{t^{\prime }}{\min }r(I_t^{a_{t^{\prime }},b_{t^{\prime }}},I_{t^{\prime }\to t})$$
其中:
$$I_t^{a_{t^{\prime }},b_{t^{\prime }}}=a_{t\to t^{\prime }}{I}_t+b_{t\to t^{\prime }}$$
其中$a_{t\to t^{\prime }}$和$b_{t\to t^{\prime }}$是根据$I_t$到$I_{t^{\prime }}$的光度变化调整。这两个参数都能以自监督方式训练。

3.几何偏差不确定

只依赖亮度变化不足以所有亮度恒定假设的失效情况。其他情况，如非朗伯曲面和运动物体，是由相应物体的固有性质引起的，这些性质对于分析建模来说并不是微不足道的。由于这些方面可以看作是观测噪声，利用Kendall等人提出的深度神经网络的异方差任意不确定性概念。预测每个像素在真实标签y的后验概率分布参数化的均值和方差的$p(y|y^{\prime },\sigma )$。例如,通过假设噪声拉普拉斯算子,负对数似是最小化:
$$-logp(y|y^{\prime },\sigma )=\frac{|y-y^{\prime }|}{\sigma }+log\sigma +const$$
不需要真实标签对$\sigma$进行训练。预测不确定性允许网络根据数据输入调整残差的权重，从而提高了模型对噪声数据或错误标签的鲁棒性。

加入不确定项的估计${\sum }_t$对提出的亮度变化不恒定的区域进行亮度变化参数预测同时加入不确定项预测值，使得几何偏差估计更加鲁棒性。
$$L_{slef}=\frac{1}{|V|}\sum _{p\in V}\frac{{\min }_{t^{\prime }}r(I_t^{a_{t^{\prime }},b_{t^{\prime }}},I_{t^{\prime }\to t})}{{\sum }_t}+log{\sum }_t$$

图2 来自KITTI和EuRoC MAV结果分析。原始图像、预测深度图和不确定度图分别从左到右显示。特别地，该网络能够预测物体边界、运动物体、高反射和高频率区域的高不确定性

总的损失函数多尺度图像上的自监督损失和正则化损失之和
$$L_{total}=\frac{1}{s}\sum _s(L_{self}^s+\lambda L_{reg}^s)$$
其中$s=4$是尺度数：
$$L_{reg}=L_{smooth}+\beta L_{ab}$$
其中：
$$L_{ab}=\sum _{t^{\prime }}(a_{t^{\prime }}-1{)}^2+b_{t^{\prime }}^2$$
亮度参数的正则化和$L_{smooth}$是$D_t$上的边缘感知平滑度.

D3VO

D3VO通过Photometric energy 和 Pose energy两个方向对深度估计中投影偏差进行改进。

1.Photometric energy

D3VO的目标是小减小深度估计和位姿估计后投影的偏差photometric error $E_{photo}$:
$$E_{photo}=\sum _{i\in \mathcal{F}}\sum _{\mathbf{p}\in {\mathcal{P}}_i}\sum _{j\in obs(\mathbf{p})}$$
​ $\mathcal{F}$是所有关键帧集合，${\mathcal{P}}_i$是关键帧$i$里的可见点，$obs(\mathbf{p})$是$\mathbf{p}$点在关键帧里可见并且当$\mathbf{p}$点在投影到关键帧$\mathbf{j}$photometric energy项：
$$E_{\mathbf{p}j}:=\sum _{\mathbf{p}\in {\mathcal{N}}_p}{w}_{\mathbf{p}}||(I_j[{\mathbf{p}}^{\prime }]-b_j)-\frac{e^{a_j}}{e^{a_i}}(I_i[\mathbf{p}]-b_i)|{|}_{\gamma }$$
​ 其中$\mathcal{N}$是$\mathbf{p}$点周围8个像素集，$a,b$是Direct sparse odometry中的非线性优化估计得相似亮度参数，$||.|{|}_{\gamma }$是Huber范数。在DSO中当具有较高的图像梯度时，对小的独立几何噪声进行补偿残差加权。我们提出用学习的方法预测不确定性参数$\sum ^{\sim }$:
$$w_p=\frac{{\alpha }^2}{{\alpha }^2+||\sum ^{\sim }(\mathbf{p})|{|}_2^2}$$
​ 这不仅依赖于局部图像的梯度，而且依赖于更高级别的的噪声模式。

​ 投影点$\mathbf{p}’$由$\mathbf{p}’=\prod (T_i^j{\prod }^{-1}(\mathbf{p},d_p))$计算得出其中$d_{\mathbf{p}}$是关键帧$i$坐标$\mathbf{p}$的深度值,$\prod (.) $是相机内参已知的重投影方程。相比传统的直接匹配方法随机初始化深度$\mathcal d_\mathbf p$我们提出初始化$\mathcal d_\mathbf p = \tilde D_i[\mathbf p] $提供矩阵尺度。本文在$E_{\mathbf pi}$的基础上加入双目视觉项$E_{\mathbf p}^+$:
$$E_{photo}=\sum _{i\in \mathcal{F}}\sum _{\mathbf{p}\in {\mathcal{P}}_i}(\lambda E_{\mathbf{p}}^{+}+\sum _{j\in obs(\mathbf{p})}{E}_{\mathbf{p}j})$$

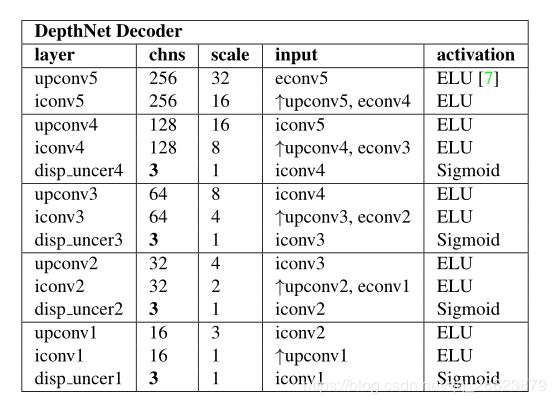
图3 深度网解码器的网络结构。所有层均为核尺寸为3、步长为1的卷积层，↑为2×2最近邻上采样。这里chns是输出通道的数量，scale是相对于输入图像的降阶因子。注意,disp_unc层有三路输出包含Dt, $D_t^s$和${\sum }_t$.

2.Pose energy

​ 与传统的直接VO方法[19,23]不同的是，该方法使用恒定速度运动模型对每个新帧初始化前端跟踪，我们利用连续帧之间的预测位姿构建非线性因子图[41,47]。具体来说，当最新的关键帧(也就是前端跟踪的参考帧)更新时，我们创建一个新的因子图。此外，从深度网络预测的相对位姿被用作当前帧和最后一帧之间的一个因子。优化完成后，我们将最后一帧边缘化，并使用因子图对后续帧进行前端跟踪。从跟踪前端估计的姿态然后用于初始化光度Bundle adjustment后端。我们在pose预测得到的位姿${\tilde{T}}_{i-1}^i$基础上得到先验位姿$T_{i-1}^i$。
$$E_{pose}=\sum _{i\in \mathcal{F}-\{0\}}Log({\tilde{T}}_{i-1}^i{T}_i^{i-1}{)}^T\sum _{{\tilde{\xi }}_{i-1}^i}^{-1}Log({\tilde{T}}_{i-1}^i{T}_i^{i-1})$$
$Log:SE(3)\to {\mathbb{R}}^6$为李代数转换矩阵，${\sum }_{{\tilde{\xi }}_{i-1}^i}^{-1}$通过在每个连续的帧对之间传播协方差矩阵得到，该协方差矩阵被建模为一个常数对角矩阵。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-5pKajDdA-1588265995260)(C:\Users\www\AppData\Roaming\Typora\typora-user-images\image-20200429234500122.png)]
图3 深度网解码器的网络结构。所有层均为核尺寸为3、步长为1的卷积层，↑为2×2最近邻上采样。这里chns是输出通道的数量，scale是相对于输入图像的降阶因子。注意,disp_unc层有三路输出包含Dt, $D_t^s$和${\sum }_t$.

3.Total energy function:
$$E_{total}=E_{photo}+w{E}_{pose}$$
如上通过在跟踪前端和优化后端引入预测姿态作为初始化，并将其作为正则化添加到光度BA的能量函数中，从而改进了直接VO方法。

PoseNet网络结构如下表

图5 PoseNet的网络结构。除了全局平均池层(avg池)，所有层都是卷积层，k为内核大小，s为步长，chns为通道，并根据输入图像缩放比例因子。

实验

1.深度估计进度对比

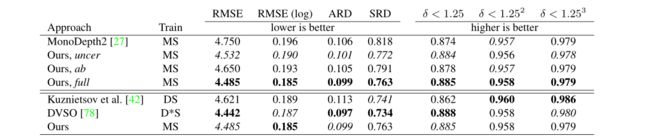
结果表明，所提出的深度估计网络在所有指标上都优于Monodepth2。研究表明，相对于Monodepth2的显著改进主要来自uncer，这可能是因为在KITTI中有许多non-Lambertian的物体，如窗户，也有独立运动的物体，如汽车和树叶，它们违反了亮度恒定假设。下表显示了与目前最先进的半监督方法的比较，结果表明我们的方法可以在不使用任何深度监督的情况下获得有竞争力的性能。

图6 在KITTI的深度评价结果。M:单目自监督;S:自监督立体监督;D:地面真深度监督;D:稀疏辅助深度监督。上半部分是与SOTA自监督网络单深度2[26]在相同设置下的对比，以及亮度变换参数(ab)和光度不确定度(uncer)的研究。下半部分是与基于深度监督和立体监督的SOTA半监督方法的比较。我们的方法在所有指标上都优于Monodepth2，也可以提供与SOTA半监督方法DVSO[78]相当的性能，该方法还额外使用了立体声DSO[74]的深度作为稀疏监督信号。*

2.亮度参数实验

首先利用原始图像对计算光度误差，然后利用PoseNet的预测参数对左侧图像进行转换计算绝对光度误差。我们还实现了一个简单的基线方法来估计仿射亮度参数通过求解线性最小二乘(LS)。我们用OpenCV[4]中实现的稠密光流方法[20]建立了正态方程。如表9所示，在进行仿射亮度变换时，平均光度误差大大降低，PoseNet的预测参数优于LS的估计参数。我们在图9中展示了更多的近似亮度变换的例子。

图7 近似亮度变换的例子在EuRoC MAV V2_O3中

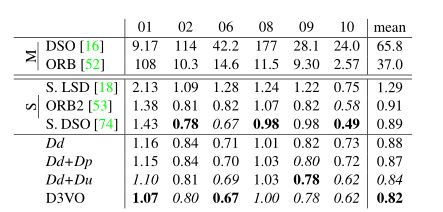
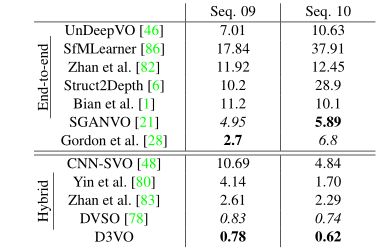
3.里程计VO结果

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-SvGgJvoc-1588236464119)(https://i.loli.net/2020/04/30/XJ85LuyaCrV9pFo.png)]

图8 关于我们的测试spilt的KITTI里程计的结果。SOTA单目(M)方法的结果如基线所示。与SOTA立体视觉方法的比较表明，D3VO在单眼视觉视觉效果上优于其他方法。此外，还对深度(Dd)、位姿(Dp)和不确定度(Du)的积分进行了研究。

图9 并与其它混合方法及端对端方法进行了比较

​

图10 从EuRoC MA V .定性比较MH 05 difficult和 V1 03 difficult的轨迹

4.训练之后的model在Cityscapes

图11 KITTI训练的模型在Cityscapes上测试结果