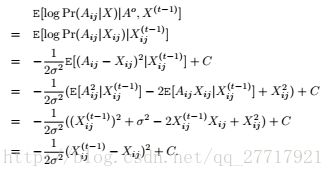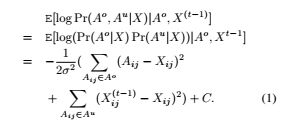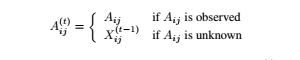基于协同过滤的SVD的推荐系统

参考论文：Using Singular Value Decomposition Approximation For Collaborative Filtering

背景：

m-n矩阵是一个打分矩阵，m是用户的数量，n为项目的数量，Ai,j表示用户i对项目j的评分情况。矩阵A一般存在两个问题。
1> 矩阵A通常非常的庞大，m、n可能有上百万或者是上亿的数量级
2> 矩阵A是一个非常稀疏的矩阵
所以我们希望可以定义一个低维矩阵X，实际上是一个线性模型，可以近似的接近矩阵A。我们通常会假设Aij = Xij+error,而error服从均值为0，标准差为
所以有
所以在给定Xi,j条件下，Ai,j的似然函数为：

我们假定 是相互独立的，则有：

我们要极大化logPr(A|X),其实就是最小化
我们可以通过极小化上面的式子找到这样的一个低维矩阵X，使得可以近似A，这就转换为最小二乘法，可以用SVD来解决此类问题，如果A被分解为了 我们获得的k个左奇异值向量矩阵U，k个奇异值的对角矩阵S以及k个右奇异向量V的转置矩阵满足

当A是一个完全已知的矩阵（就是表示A中的所有元素都不是稀疏的），我们就可以通过SVD对矩阵A分解

就可以看作是最可能或者说是最能表达矩阵A的秩为k的矩阵了，显然我们把一个求极大似然估计的问题转换为了对矩阵A的SVD的矩阵分解问题。
但是SVD的矩阵分解存在着两个问题：

1. 矩阵A的稀疏程度会影响推荐系统的推荐准确率，在稀疏情况下，SVD的矩阵分解通常会出现过拟合的问题。

2. SVD分解的复杂度比较高，假设对一个m*n的矩阵进行分解，时间复杂度为O(n^2*m+n*m^2)，其实就是O(n^3)。对于m、n比较小的情况，可能是可以受的，但是在海量数据下，m和n的值通常会比较大，可能是百万级别上的数据，这个时候如果再进行SVD分解需要的计算代价就是很大的。
   所以针对上面两个提出的问题，分别提出了解决方案。

矩阵A数据稀疏问题

A矩阵存在多个缺失值的问题就可以看作是数据稀疏问题。比如用户-项目的评分矩阵，通常会用用户对所有项目的评分均值或者是对项目评分的均值来取代对应的位置，然后再建立线性模型（其实就是SVD分解）拟合矩阵A，但是通常用这种比较原始的方法来拟合矩阵可能会出现用错误的模型拟合出来与正解偏差更大的值，然后根据错误的值拟合模型，从而使得整个模型也出现问题。所以我们一般会利用EM过程建立模型极大化可观测值(observed data)（其实就是矩阵A中没有缺失的值），EM过程中的隐数据(unknow data）就是矩阵A中缺失的值。
这里记
隐数据为
可观测数据为
参数为X
Expection
E步是求在当前t下的参数以及可观测的田间下隐数据的条件分布的期望。

确定EM函数的E步，首先要确定起着核心作用的Q函数

这里的Q函数：

X表示参数，其实就是我们极大似然最大情况下近似的表示矩阵A的矩阵，我们要求的就是X。在存在可观测数据和隐数据的情况下估计参数就需要利用EM算法。
如果Ai,j是可观测数据，则有

如果Ai,j是隐数据，则有

综合上面两种情况：

Maxization
M步极大化E步中的Q函数下的参数X，从t-1步的X更新为t步的X。

我们要获得 极大化Q函数，需要极小化下式：

我们可以把上面这个式子通过规范

我们的目标转换为极小化

根据我们在前面的分析，达到上式中的极小情况，可以用SVD来解决，对SVD分解就能得到X，而这个X则是能满足的这个最小平方差的矩阵了。
如果我们能在EM算法中对每一步的A进行SVD分解，然后不断更新X，直到收敛，那么我们就能够通过Xi,j来预测用户i对项目j的预测了，并且这是最为理想的预测结果。

但是问题又来了，在每一步我们都要对 进行SVD分解，那么如果迭代l步才能达到收敛，得到稳定的X，我们的时间复杂度则为l*O(n^2*m+m^2*n)，这在m、n都很大的情况下显然是不能被接受的。所以可以基于采样来减少计算的复杂度。

降低计算复杂度

我们希望评分矩阵A很大，我们能不能转换成在一个维数小的矩阵上进行SVD分解出来的矩阵能近似等于矩阵A，所以有了在矩阵A上进行行向量采样的想法。

我们在一定规模上采样矩阵A的c行组成一个c*n的矩阵C，矩阵C的右奇异矩阵能近似等同矩阵A的右奇异值矩阵，从矩阵A中取到i行的概率记为pi，
Beta为常量，||*||表示向量的长度。
对矩阵A采样行向量得出的矩阵C进行SVD分解，假定取k个奇异值就能包含矩阵C的90%的能量，记C的右奇异值矩阵为H，H为一个n*k的矩阵，记 为一个最能近似表示矩阵A的秩为k的矩阵，整个EM过程就变为，
t步下的E过程：
计算C的k个右奇异向量，组成矩阵H
当计算出H后，用 近似
t步下的M过程：
用（） i,j近似的表示Ai,j。
下面是算法的详细过程：

时间复杂度

最终EM过程的SVD分解的时间复杂度为l*O(c^2*n+c*n^2),c要远小于m，因而时间复杂度能够得到很好的优化，另外还有一个注意点是：m是所有用户的数量，我们在采样c行代表c个用户打分信息，并不要求这c行必须是不同的用户，并且一个用户可以被采样多次，所有矩阵C可能会出现多行数据相同的情况。

另外，除了在C上直接计算左奇异矩阵，可以通过计算CCT的特征向量，计算C的右奇异矩阵可以通过CTC的特征向量，具体可以参见博客