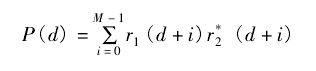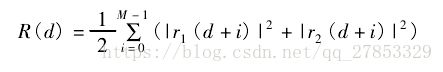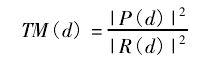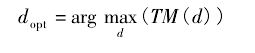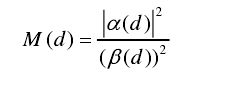4G同步的自我总结

LTE的下行同步

同步的目的

LTE系统的同步是UE在接收端进行数据处理前首先需要完成的过程，通过同步过程获得的定时同步和频率同步信息，可以确定发射端无线数据帧的帧头位置、OFDM符号的起始位置、以及载波频偏并完成对频偏的补偿。此外，通过同步过程还可以完成小区搜索，其获得的小区ID是UE接入小区的保证。同步算法的性能会直接影响LTE后续的通信过程。

在LTE系统中，接收端不知道发射端信号的起始时刻，且由于多径及噪声的影响信号时延也未知，因此在进行数据处理之前，需要确定传输的数据帧的帧头，即进行帧定时同步。为了对接收信号正确进行OFDM解调，需要知道OFDM符号的起始位置，即进行符号定时同步。由于LTE系统采用了MIMO-OFDM结合的技术，而多普勒频移和收发两端振荡器的频率偏移会破坏OFDM子载波的正交性，从而造成子载波间干扰，因此需要估计出频率偏移并对其补偿，即进行载波频率同步。

小区搜索

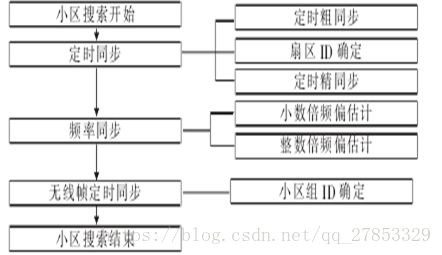
   LTE系统中，同步过程的第一步是进行下行同步，即小区搜索。当用户进行切换和初始接入时，使用小区搜索过程识别并获得小区下行同步，读取小区的广播信道信息。在LTE系统中，标准确定的小区搜索整体流程如图所示。

定时同步

对LTE系统小区搜索的定时同步分为定时粗同步和定时精同步两个步骤。

粗同步

定时粗同步算法的基本原理如下:令M为时域序列自相关窗口的长度，r1, r2分别为一个无线帧的两个半帧时域接收序列，则定义相关函数为：

前后两个相关窗口的平均能量可计算为：

于是定时测度函数为：

则目标定时粗同步位置：

 

sc算法介绍

SC算法是由Schmidl & Cox在1997年提出的用于OFDM系统的经典算法。该算法也可用于LTE系统中，因为10ms无线帧中的前后两个PSS是相同的，通过对这两个PSS进行自相关，定时度量函数的最大值位置，即为定时同步点。

sc算法的定时度量函数表示如下:

其中d表示定时滑动窗的起始采样点位置，a(d)表示前后两个PSS的自相关值，β(d)表示第二个PSS的能量值。

定时度量函数M(d)取得最大值时，即可得到PSS的起始位

d=argmax{M(d)}

 sc算法的定时度量函数峰值并不一定会出现在正确的定时同步位置点，因为CP的存在，定时度量函数M(d)会在整个CP范围内出现一个峰值平台，而不会出现尖锐的峰值。

比如:

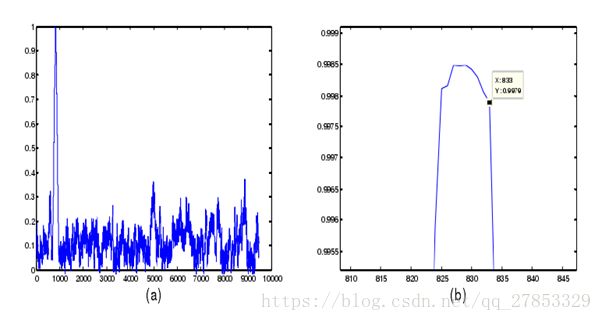
在半帧的搜索范围内，定时度量函数如图(a)所示，对左图中的峰值附近进行放大，如图(b)所示，正确的定时同步点为第833个采样点并不是度量函数的最大值点，而若按图中取最大值，则定时同步点会不准确。

定时同步点:833=(2048/16)*6+160/16+(144/16)*6+1

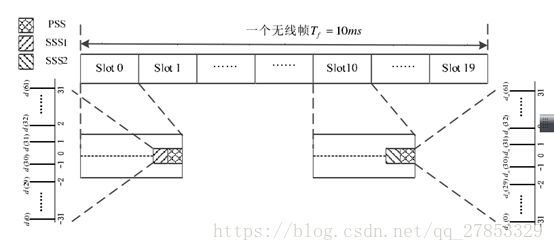
（16倍下采样，PSS在FDD中位于时隙0的最后一个OFDM符号)

FDD下的位置

精同步

在粗同步时已将主同步信号的位置锁定在一个较小的范围内，由此只需要在该范围内对主同步信号进行进一步的搜索。

基本原理是利用本地预先生成的三组主同步信号经过128点FFT运算(2 048点的1/16降采样)，再由定时粗同步得到的定时范围用基于互相关的同步算法分别与接收数据进行滑动相关;然后从三组相关结果中找出最大值所在对应位置即可获得主同步信号的位置，确定系统所用的主同步信号类型，因此也得到了生成该类型主同步信号的物理层小区组内标志NID2

互相关算法的相关函数定义：

定时精同步的位置为

频率同步

载波频偏估计分为小数倍频偏估计和整数倍频偏估计。当移动终端UE与网络基站之间的绝对频率偏差未超过子载波间隔的一半时，就会产生可估计的小数倍频偏。小数倍频偏会破坏OFDM子载波之间的正交性，直接导致接收端的基带时域信号产生相位变换，不能正确恢复出发送端数据。

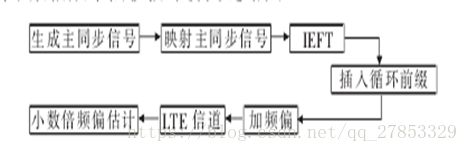
小数倍频偏估计

小数倍频率偏移估计仿真链路图如下：

提出一种基于PSS的算法，以LTE物理层最低带宽1.4MHz为例，发送端发送的主同步信号m_k= {a_k} 1≤k≤128，其中{ a_k }为主同步信号时域复数序列。假设符号定时同步精确，接收端接收到的主同步信号可以表示为:

将接收的主同步信号与发送的主同步信号进行共扼乘得:

得到的似然函数为:

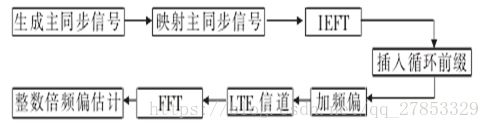
整数倍频偏估计

 当移动终端UE与网络基站之间的绝对频率偏差超过子载波间隔的一半时，就会产生可估计的整数倍频偏。整数倍频偏不会破坏OFDM子载波之间的正交性，但它会使得经FFT过后频域上的数据产生偏移现象，直接导致接收端的基带频域信号产生循环移位。其中整数倍频偏的大小决定了循环移位的偏移个数，即当频偏是子载波间隔的n ( n为整数)倍时，经FFT过后的频域数据也会偏移n个子载波位置，跑到其他子载波上去，因而不能正确恢复出发送端数据。但是偏移后的数据并没有在数值上受到影响，因此只要估计出频域数据偏移的位置个数，即可估计出整数倍频偏的大小。

 

整数倍频偏估计仿真链路

主同步信号具有良好的频域自相关性，利用接收信号解调后的数据与原来发送的本地信号进行相关运算，得到一个峰值。当不存在频偏时，即频域内解调的数据没有发生循环移位时，其与发送信号作相关后峰值出现在相关后序列正中间的位置上;当存在n个整数倍的频偏时，相关序列的峰值位置则出现在与正中间相距n个点的位置上。因此利用峰值位置与中心位置相距的点数就能推出实际存在的整数倍频偏。

无线帧定时同步

传统SSS盲检测算法

 传统的sss检测算法是将本地产生的sss序列与接收sss序列互相关，通过相关峰值确定小区ID组号及子帧号，从而实现小区ID组号的检测及帧定时同步。由于小区ID组号有168种可能取值，且SSS序列的子帧0和子帧_5的产生规则不同，因此采用该算法需要将提取出的接收SSS序列与168X2个本地的SSS序列进行相关。

一般的SSS检测算法

 

 

 该算法主要利用SSS的生成规则，根据PSS定时同步已经检测出的小NID2号，逆向解扰，最后求出小区组号NID1。该算法的检测流程如下:

 （1）由式可知SSS频域序列的产生是分为奇偶的，因此首先将频的SSS序列d(k)按奇偶分开，分别得到d(2k)和d(2k + 1)。

(2)由扰码序列ci (n)生成规则，根据PSS定时同步中检测出的小区ID号NID2，解出扰码序列ci (n)

(3)由解出的与偶序列d(2k)，计算出。i根据子帧为0或5的不同，可能有i=0或i=1。

 (4)考虑到取值范围[0, 29]，的取值范围[1, 30]，对m在[0, 30]范围，产生31组本地序列，分别与第(3)步中计算出的的进行相关，相关峰值对应的m，即可估计出或其中一个的值。

(5)计算扰码序列，再利用d(2k+1)与，计算出

(6) 将产生的31组本地序列，分别与第(5)步中计算出的 作相关，取相关峰值对应的m，即可估计出或中另外一个的值。

(7)最后由m0和m1通过查找表，确定小区ID组号NID1。

0	0	1	34	4	6	68	9	12	102	15	19	136	22	27

1	1	2	35	5	7	69	10	13	103	16	20	137	23	28
2	2	3	36	6	8	70	11	14	104	17	21	138	24	29
3	3	4	37	7	9	71	12	15	105	18	22	139	25	30
4	4	5	38	8	10	72	13	16	106	19	23	140	0	6
5	5	6	39	9	11	73	14	17	107	20	24	141	1	7
6	6	7	40	10	12	74	15	18	108	21	25	142	2	8
7	7	8	41	11	13	75	16	19	109	22	26	143	3	9
8	8	9	42	12	14	76	17	20	110	23	27	144	4	10
9	9	10	43	13	15	77	18	21	111	24	28	145	5	11
10	10	11	44	14	16	78	19	22	112	25	29	146	6	12
11	11	12	45	15	17	79	20	23	113	26	30	147	7	13
12	12	13	46	16	18	80	21	24	114	0	5	148	8	14
13	13	14	47	17	19	81	22	25	115	1	6	149	9	15
14	14	15	48	18	20	82	23	26	116	2	7	150	10	16
15	15	16	49	19	21	83	24	27	117	3	8	151	11	17
16	16	17	50	20	22	84	25	28	118	4	9	152	12	18
17	17	18	51	21	23	85	26	29	119	5	10	153	13	19
18	18	19	52	22	24	86	27	30	120	6	11	154	14	20
19	19	20	53	23	25	87	0	4	121	7	12	155	15	21
20	20	21	54	24	26	88	1	5	122	8	13	156	16	22
21	21	22	55	25	27	89	2	6	123	9	14	157	17	23
22	22	23	56	26	28	90	3	7	124	10	15	158	18	24
23	23	24	57	27	29	91	4	8	125	11	16	159	19	25
24	24	25	58	28	30	92	5	9	126	12	17	160	20	26
25	25	26	59	0	3	93	6	10	127	13	18	161	21	27
26	26	27	60	1	4	94	7	11	128	14	19	162	22	28
27	27	28	61	2	5	95	8	12	129	15	20	163	23	29
28	28	29	62	3	6	96	9	13	130	16	21	164	24	30
29	29	30	63	4	7	97	10	14	131	17	22	165	0	7
30	0	2	64	5	8	98	11	15	132	18	23	166	1	8
31	1	3	65	6	9	99	12	16	133	19	24	167	2	9
32	2	4	66	7	10	100	13	17	134	20	25	-	-	-
33	3	5	67	8	11	101	14	18	135	21	26	-	-	-