本篇文章讨论的是对火箭问题的建模。
-
- 火箭问题的提出
- 卫星的速度
- 火箭的推力
- 火箭系统的质量
- 多级火箭的速度公式
火箭问题的提出
假如要向地球轨道内发生一颗火箭,火箭在上升过程中,因为动力不足,通过会分成多级火箭,在发生到一定程度时,在半空中点燃第二级火箭,给火箭继续提供动力到达绕地球的轨道内,使得在轨道内,卫星能在地球的引力作用下,环绕地球旋转。
那火箭在到达地球之后应该以什么速度运动,才能刚好在不脱离地球的同时,也不坠落,能在轨道上持续运动呢?这是火箭发射的主要研究问题。为了解答这一问题,我们必须对该问题建模,既然要夹馍,肯定需要找出这个过程的主要因素是什么?我们发现主要的因素是火箭到达特定轨道时的运动速度是多少?而速度是通过加速度起作用的,由力与加速度的关系公式:
F=m a
我们发现如果要让火箭获得较大的速度,必须让火箭具有较大的力和较小的质量,从中,我们可以确定整个建模的过程中需要讨论的四个主要因素:
- 卫星的速度
- 火箭的推力
- 火箭与卫星的质量
- 最佳的级数
一般火箭要经过多级加速的。
这就是我们接下来要讨论的主要问题。
卫星的速度
牛顿法开普勒三大定律之上,建立起了两个物体之间的万有引力定律:宇宙万物之间都存在着相互吸引的引力,它的作用方向在两个物体的连线上,它的大小与两者质量的乘积成正比,而与两者距离的平方成反比,且比例系数是一个对万物都相同的宇宙常数。用公式表示为:
G=γMmr2
γ 表示万有引力常数,M表示地球的质量,m表示卫星的质量,r表示卫星到地球中心的距离。
假设 k=γM,k 表示地球引力常数,万有引力公式可以表示为
G=kmr2
又已知地球表面的重力加速度为g,根据牛顿第二定律有:
kmR2=mg
可以得到地球引力常数为:
k=R2g
当卫星绕地球做匀速圆周运动是,卫星没有切向的加速度,卫星的法向加速度为
v2r ,由万有引力定律可得:
mv2r=mg(Rr)2
左边为转动惯性力,使得卫星在地球轨道上运动而不掉下来,对该式子求解可以得到:
v=Rgr‾‾√
这就是卫星绕地球旋转应该由的速度。那么火箭的速度也应该达到这个速度,计算可得:
v=Rg=7.9 km/s
这是我们解决的第一个问题,火箭的速度。
火箭的推力
我们把火箭抽象成仅由一个动力系统和动力舱组成的物体,采用微元法,根据质量守恒和动量守恒,考察火箭在 [t,t+∇t] 时刻的动量变化,t时刻火箭系统的动量就是 m(t)v(t) ,在 t+∇t 时刻,动量分为两个部分,一部分表示火箭的动量
m(t+∇t)v(t+∇t)
另一部分表示火箭产生的气体的动量
(m(t)−m(t+∇t))(v(t)−u)
式中u表示气体相对于火箭的速度,而
v(t) 表示火箭相对于地球的速度,因为气体相对于火箭的速度和火箭相对于地球的速度大小相等,方向相反,故气体相对于地球的速度就为
v(t)−u .因此,根据动量守恒定律有:
m(t)v(t)=m(t+∇t)v(t+∇t)−(m(t+∇t)−m(t))(v(t)−u)
将方程化简为:
lim∇t→0m(t+∇t)v(t+∇t)−m(t)v(t)∇t=lim∇t→0(m(t+∇t)−m(t))(v(t)−u)∇t
即表示如下微分方程:
d(m(t)v(t))dt=dm(t)dt(v(t)−u)
将左边乘积的导数化简,可以得到这样一个常微分方程:
m(t)dv(t)dt=−um(t)dt
使用分离变量法,可以求得
v(t)=v0+u Inm0m(t)
m0 表示火箭的初速度,一开始为静止状态,故为零。
火箭系统的质量
考虑火箭的质量,主要包含三个部分,火箭的有效载荷,用 mp 表示,火箭的结构质量,用 ms 表示;以及火箭所装载的燃料的质量,用 mf 表示,火箭的初始质量可以表示为:
m0=mp+ms+mf
但我们真正关心的是火箭到达轨道附近,换句话说,就是火箭燃烧完之后的质量是多少,以及对应的速度是多少,由前文质量火箭的速度可以由公式得到:
v=u Inm0mp+ms
为了求解方便,我们再定义一个量-结构比:
λ=msms+mf ,因此有:
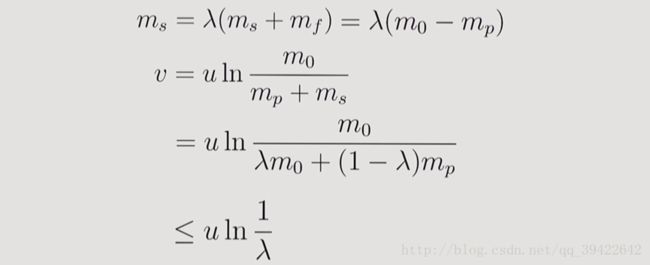
如果结构比足够小,或者气体的速度足够大,都能达到卫星在地球轨道上运行的速度,但这些条件都不是想要多少就有多少的,很多都受限于当时的技术水平,目前的水平来看,气体的速度可以为:
u=3 km/s,λ=0.1 ,y因此一般
v<=3 In10=7 km/s
因此,如果使用一级火箭,在现有的技术 水平下,发射火箭的速度无法达到7.9。
多级火箭的速度公式
由牛顿第二定律:
F=m a
我们知道,如果要让火箭获得gendarme的速度,可以增加加速度,但推力室一定的,所以减少火箭的质量,就变成了一个唯一可行的方案了。我们可以设想出多级火箭,在某一级火箭的燃料耗尽后,发射第二级火箭,同时去掉一部分外壳,使得质量有所下降。
因此,仍然假设结构比为 λ, 共有n级火箭,各级火箭的结构质量和对应的燃料质量总和分别为 m1,m2,⋯,mn ,所以第i级火箭的结构质量为 λmi, 地i级火箭的燃料质量为 (1−λ)mi . m0=mp+m1+m2+⋯+mn.
当第一级火箭燃尽时,由于初始速度为0,因此当第一级火箭燃尽时的速度为
v1=u Inm0mp+λm1+m2+⋯+mn
,将第一级火箭的接哦股丢弃,仍然用前面的公式,但这时候的初始速度不为零,而是第一级火箭燃尽时的速度作为初速度。而且,当第二级火箭燃料燃尽时,它的质量为
m+p+m2+m3+⋯+mn ,由此类推,可以得到当第i级火箭燃尽时的速度为:
vi=vi−1+u∗In mp+mi+⋯+mnmp+λmi+mi+1+⋯+mn
由此可以得到火箭的最终速度为:
v=u In(m0mp+λm1+m2+⋯+mn∗⋯∗mp+mnmp+λmn)
总结
数学建模的关键在于精确得确定问题,并找出影响结果的主要因素是什么。今儿一步一步的分析这些因素。
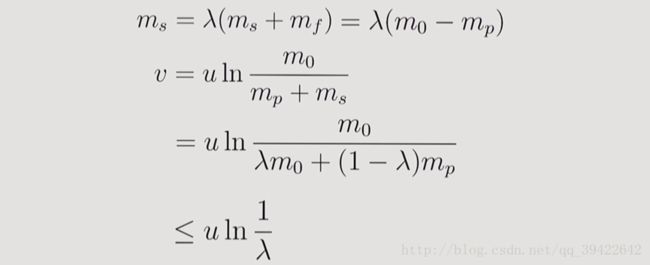 如果结构比足够小,或者气体的速度足够大,都能达到卫星在地球轨道上运行的速度,但这些条件都不是想要多少就有多少的,很多都受限于当时的技术水平,目前的水平来看,气体的速度可以为:
u=3 km/s,λ=0.1 ,y因此一般
如果结构比足够小,或者气体的速度足够大,都能达到卫星在地球轨道上运行的速度,但这些条件都不是想要多少就有多少的,很多都受限于当时的技术水平,目前的水平来看,气体的速度可以为:
u=3 km/s,λ=0.1 ,y因此一般