堆与堆排序,最大索引堆(python实现)
-
- 优先队列与堆
- 最大堆的基本结构与实现
- 基本操作1插入一个元素
- 基本操作2取出一个元素
- 初始化堆
- 原地堆排序
- 索引堆
- 堆的拓展问题
优先队列与堆
普通的队列是先进先出,后进后出的。但对于优先队列来说,出队的顺序不取决于入队的顺序,而取决于他们的优先次序。最简单的优先队列案例就是医院的急诊病人,明明已经有病人在等候了,但急诊病人往往会优先,这其实就是优先队列。
为什么要使用优先队列呢?
如果要在N个元素的数组中选出前M个元素,一般的想法就是排个序,然后选出前M个元素,这样的算法复杂度为 O(NlogN) O ( N l o g N ) ,但如果使用优先队列,算法的复杂度就会降为 O(NlogM) O ( N l o g M ) .
优先队列的基本操作和一般队列类似,都是入队和出队,唯一不同的是,优先队列的出队顺序根据优先级来确定。如果有N个请求,使用普通数组最糟糕的情况可能需要 O(N2) O ( N 2 ) 的时间复杂度,但如果使用堆,时间复杂度就会降为 O(NlogN) O ( N l o g N )
最大堆的基本结构与实现
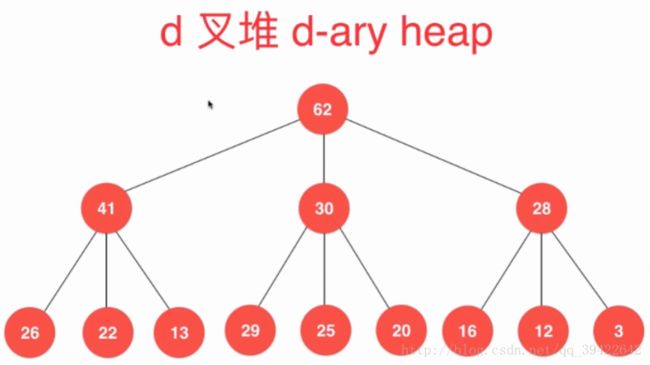
堆的结构是一个树型的结构,相应的二叉堆,则是一颗二叉树,主要满足两个条件:
- 父节点大于两个子节点
- 二叉堆又是一颗完全的二叉树:完全的二叉树是指对于所有节点的个数必须是最大值,且元素必须是从左到排的
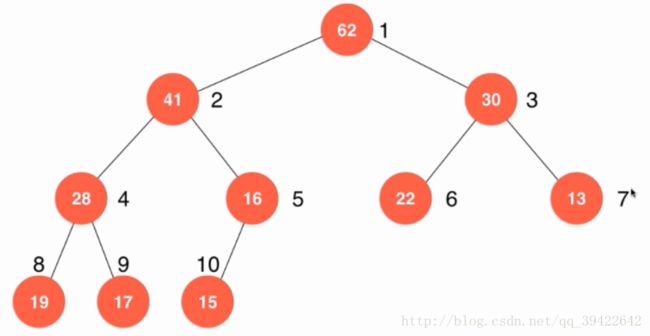
一般的,我们使用数组来存放最大堆,如图所示, 我们的数组是根节点从1开始的,0号索引是不使用的。它们满足的性质为:
- 父亲节点:i
- 左孩子节点: 2∗i 2 ∗ i
- 右孩子节点: 2∗i+1 2 ∗ i + 1
基本操作1:插入一个元素
插入一个元素相当于在元组的末尾放一个元素,如图所示,在索引为11的位置加入53,但为了维护最大堆的性质,我们需要调整一下52的位置,这个操作就是shift up,它的主要操作就是比较一下它和它的父节点的大小,如果52比它的父节点元素还要大,就交换一下位置,知道满足堆的性质。
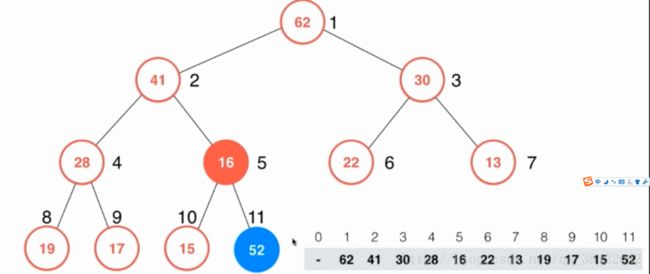
注:为了方便调用,我把这些操作都封装到类中了
class MaxHeap(object):
def __init__(self,max = 100000):
self.heapList = [0]
self.currentSize = 0
self.maximum = max
def insert(self,k):
#从堆中插入一个元素
self.heapList.append(k)
self.currentSize += 1
self.shiftUp(self.currentSize)
if self.currentSize > self.maximum:
self.delFirst()
#从堆中插入一个元素的辅助函数
def shiftUp(self,i):
currentvalue = self.heapList[i]
while i//2 > 0:
if self.heapList[i//2] < currentvalue:
self.heapList[i] = self.heapList[i//2]
i = i//2
else:
break
self.heapList[i] = currentvalue
基本操作2:取出一个元素
取出一个元素要注意,最大堆只能取出根节点的元素,也就是最大的元素62,然后把最后一个元素16放到根节点的位置,然后索引直接-1,就完成一半了。你可能想到了,要是这么做,根节点的元素已经不满足最大堆的性质了,这是就要设计一个算法 shift down,使得堆依旧满足最大堆的性质。

其实也很简单,只要比较一下它的两个孩子节点谁大,然后拿大的孩子节点52和根节点16(当前节点)比较一下,如果比孩子节点小,就交换一下位置,即16和52交换一下位置即可。

python实现
def shiftDown(self,i):
currentValue = self.heapList[i]
while i*2 <= self.currentSize:
mc = self.maxChild(i)
if self.heapList[i] < self.heapList[mc]:
self.heapList[i] = self.heapList[mc]
i = mc
else:
break
self.heapList[i] = currentValue
def maxChild(self,i):
if 2*i + 1 > self.currentSize:
return 2*i
else:
if self.heapList[i*2] < self.heapList[i*2 + 1]:
return 2*i + 1
else:
return 2*i
def delFirst(self):
retVal = self.heapList[1]
if self.currentSize == 1:
self.currentSize -= 1
self.heapList.pop()
return retVal
self.heapList[1] = self.heapList[self.currentSize]
self.heapList.pop()
self.currentSize -= 1
self.shiftDown(1)
return retVal初始化堆
怎么把一个数组转换成一个堆呢?
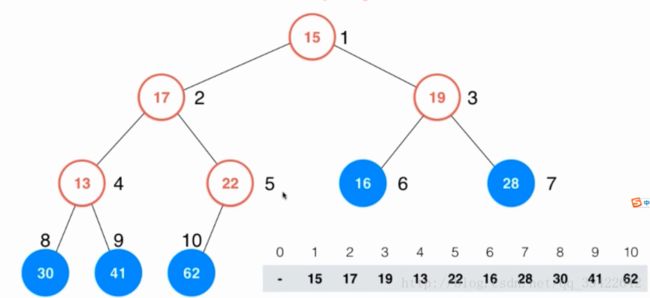
我们把一个数组转换为堆的过程称为heapify。对于一颗完全的二叉树,它的所有叶子节点,也就是图中绿色的部分,其实已经是一个单独的堆了,那第一个不是叶子结点的元素是 n2 n 2 ,比如图中有10个元素,那 102=5, 10 2 = 5 , 因此第一个不是叶子节点的元素为索引为5的位置,刚好正确。我们只要考察一下每一个不是叶子结点的节点,看它是否满足最大堆的性质(用shift down)就好了。
def heapify(self,arr):
self.currentSize = len(arr)
i = len(arr)//2
self.heapList = [0] + arr[:]
while(i > 0):
self.shiftDown(i)
i -= 1
return self.heapList将n个元素插入到一个空堆中,算法复杂度为 O(NlogN) O ( N l o g N ) ,heapify的过程。算法复杂度为 O(n) O ( n )
原地堆排序
我们发现,对于最大堆来说,根节点的元素总是最大的,因此,如果每次都把根节点的元素和最后的元素互换位置,然后再把堆的跟节点进行一次shift down,那么最后一个元素就是整个数组的最大值,基于这个思想,如果不断进行这样的操作,利用堆的性质,就可以让一个数组最终从大到小排序。

def heapSortInPlace(self,arr):
self.heapify(arr)
while self.currentSize > 1:
self.heapList[1],self.heapList[self.currentSize]=self.heapList[self.currentSize],self.heapList[1]
self.currentSize -= 1
self.shiftDown(1)
return self.heapList[1:] #注意索引为0的位置我们没有使用索引堆
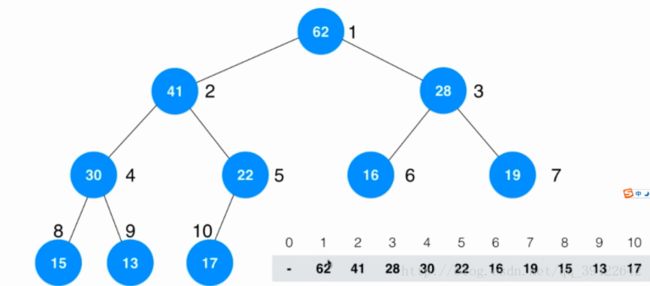
我们先来看一下堆这个数据结构的问题,假如数组中一个元素代表了一个很长的字符串,当把这个数组通过heapify转化为堆时,需要交换元素的位置,这时候计算资源的消耗是巨大的,这个尚且可以通过技术手段来缓解,但另一个非常致命的问题,由于我们的元素在整个数组中的位置发生了改变,使得我们很难索引到它,如果要对其更改,就变得非常困难了。
如图所示为构建堆之后的数组,数组中的元素在数组中的位置发生改变之后,相应的索引已经发生了改变,我们很难对这些元素进行重新定位
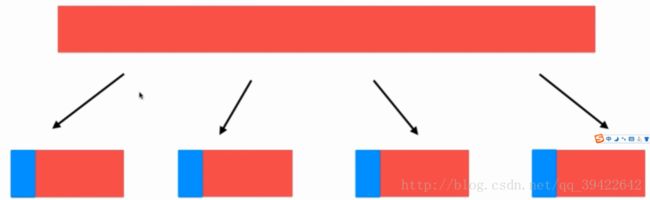
针对这个问题,我们可以构建一个索引,分别定位每隔元素,如图:

而这个的堆不再是堆元素直接操作,而是对他们的索引操作,将他们的索引构建成堆的数据结构,而不去动原数组的元素,当需要改变数组的元素时,通过索引来定位相应的元素以完成更改的操作。


因此我们在做元素比较的时候比较的是原数组data中的元素,而做交换的是索引index数组中的元素。
使用python中的dict可以很容易的实现最大索引堆:
class IndexMaxHeap(object):
def __init__(self):
self.indexList = [0]
self.items = {}
self.currentSize = 0
def insert(self,k,value):
self.indexList.append(k)
self.items[k] = value
self.currentSize += 1
self.shiftUp(self.currentSize)
def shiftUp(self,i):
currentValue = self.items[self.indexList[i]]
currentIndex = self.indexList[i]
while i//2 >0:
if self.items[self.indexList[i//2]] < currentValue:
self.indexList[i] = self.indexList[i//2]
i = i//2
else:
break
self.indexList[i]= currentIndex
def delFirst(self):
retVal = self.items[self.indexList[1]]
del self.items[self.indexList[1]]
if self.currentSize == 1:
self.currentSize -= 1
self.indexList.pop()
return retVal
self.indexList[1] = self.indexList[self.currentSize]
self.indexList.pop()
self.currentSize -= 1
self.shiftDown(1)
return retVal
def shiftDown(self,i):
currentvalue=self.items[self.indexList[i]]
currentindex=self.indexList[i]
while i*2<=self.currentSize:
mc=self.maxChild(i)
if currentvalue < self.items[self.indexList[mc]]:
self.indexList[i]=self.indexList[mc]
i=mc
else:
break
self.indexList[i]=currentindex
def maxChild(self,i):
if 2*i + 1 > self.currentSize:
return 2*i
else:
if self.items[self.indexList[2*i]] > self.items[self.indexList[2*i + 1]]:
return 2*i
else:
return 2*i + 1
def heapify(self,items):
self.items = items
self.indexList = [0] + list(self.items.keys())
self.currentSize = items.__len__()
i = self.currentSize//2
while i > 0:
self.shiftDown(i)
i -= 1
def buildHeap(self,items):
self.items=items
self.indexList=[0]+list(self.items.keys())
self.currentSize=items.__len__()
i=self.currentSize//2
while i>0:
self.shiftDown(i)
i-=1
def getItem(self,i):
return self.items[i]
def maxItemIndex(self):
return self.indexList[1]
def change(self,k,value):
if k not in self.indexList:
raise Exception('%s is out of index!'%k)
self.items[k] = value
i = self.indexList.index(k)
self.shiftDown(i)
self.shiftUp(i)
return True
heap=IndexMaxHeap()
items={'John':21,'Lucy':14,'Jesscia':17,'张三':32,'李四':11} #按照分数构成最大堆
heap.buildHeap(items)
heap.insert('Dark',15)
print('最高分: %s %s' % (heap.maxItemIndex(),heap.items[heap.maxItemIndex()]))
print('Lucy多少分? %s' % heap.getItem('Lucy'))
#将Lucy的分数提高到50
heap.change('Lucy',50)
print('最高分: %s %s' % (heap.maxItemIndex(),heap.items[heap.maxItemIndex()]))
heap.delFirst()
print('最高分: %s %s' % (heap.maxItemIndex(),heap.items[heap.maxItemIndex()]))输出:
最高分: 张三 32
Lucy多少分? 14
最高分: Lucy 50
最高分: 张三 32堆的拓展问题
1.可以用堆来实现优先队列
4.最大最小队列
思路:既放一个最大堆,也放一个最小堆,两个堆同时维护一组数据
5.更多的堆还有二项堆,斐波那契堆