第五届省赛（软件类）真题----Java大学A组答案及解析

第五届省赛（软件类）真题—-Java大学A组答案及解析

1. 子序列最大长度
2. 莱布尼茨公式
3. n的n次幂
4. 七对数字
5. 勾股定理
6. 九阶数独
7. 矩阵射线

一、子序列最大长度

一个串的子串是指该串的一个连续的局部。如果不要求连续，则可称为它的子序列。
比如对串： “abcdefg” 而言，”ab”,”abd”,”bdef” 等都是它的子序列。
特别地，一个串本身，以及空串也是它的子序列。
对两个串而言，可以有许多的共同的子序列，我们关心的是：它们所共同拥有的长度最大的子序列是多长。以下代码实现了这个问题的求解。请填写划线部分缺失的代码。
注意：只填写缺少的代码，不要写任何多余的内容，比如注释或说明文字。

public class Zixulie
{
    public static int f(String x, String y)
    {
        if(x.length()==0) return 0;
        if(y.length()==0) return 0;

        String x1 = x.substring(1);
        String y1 = y.substring(1); 

        if(x.charAt(0)==y.charAt(0)) return f(x1,y1)+1;

        return____________________;
    }

    public static void main(String[] args)
    {
        System.out.println(f("ac","abcd")); //2
        System.out.println(f("acebbcde1133","xya33bc11de")); //5
    }
}

答案：Math.max(f(x1, y), f(x, y1))

---

二、莱布尼茨公式

历史上有许多计算圆周率pai的公式，其中，格雷戈里和莱布尼茨发现了下面的公式：

这个公式简单而优美，但美中不足，它收敛的太慢了。
如果我们四舍五入保留它的两位小数,那么：

累积1项是：4.00
累积2项是：2.67
累积3项是：3.47
。。。
请你写出它累积100项是多少（四舍五入到小数后两位）。
注意：只填写该小数本身，不要填写任何多余的说明或解释文字。

答案：3.13

public class Main {
    public static void main(String[] args) {
        float sum = 0;
        float flag = 1;
        for (int i = 1; i <= 2*100-1; i += 2) {
            sum += flag * 1.0 / i;
            flag = -flag;
        }
        System.out.printf("%.2f", sum*4);
    }
}

---

三、n的n次幂

如果x的x次幂结果为10（参见【图1.png】），你能计算出x的近似值吗？

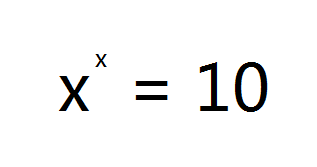
显然，这个值是介于2和3之间的一个数字。
请把x的值计算到小数后6位（四舍五入），并填写这个小数值。
注意：只填写一个小数，不要写任何多余的符号或说明。

答案：3.162278

public class Main {
    public static void main(String[] args) {
        System.out.println(sqrt(10));
    }
    /**
     * 牛顿迭代法开平方
     * */
    public static double sqrt(double c)
    {
        if(c < 0)
        {
            return Double.NaN;
        }
        double err = 1e-15;
        double t = c;
        while(Math.abs(t - c/t) > err*t)
        {
            t = (c/t + t)/2.0;
        }
        return t;
    }
}

---

四、七对数字

今有7对数字：两个1，两个2，两个3，…两个7，把它们排成一行。
要求，两个1间有1个其它数字，两个2间有2个其它数字，以此类推，两个7之间有7个其它数字。如下就是一个符合要求的排列：

17126425374635

当然，如果把它倒过来，也是符合要求的。
请你找出另一种符合要求的排列法，并且这个排列法是以74开头的。
注意：只填写这个14位的整数，不能填写任何多余的内容，比如说明注释等。

答案：74151643752362

public class Main {
    static int[] s;
    public static void main(String[] args) {
        s = new int[]{0, 7, 4, 0, 0, 0, 0, 4, 0, 7, 0, 0, 0, 0, 0};
        dfs(1);
        for (int i = 1; i < s.length; i++) {
            System.out.print(s[i]);
        }
    }
    public static int dfs(int n) {
        if (n == 4) {
            n++;
        }
        if (n > 6) {
            return 1;
        }
        for (int i = 3; i <= 14; i++) {
            if ( i == 7 || i == 9) {
                continue;
            }
            if (i+n+1 <= 14 && s[i] == 0 && s[i+n+1] == 0) {
                s[i] = s[i+n+1] = n;
                if (dfs(n+1) != 0) {
                    return 1;
                }
                s[i] = s[i+n+1] = 0;
            }
        }
        return 0;
    }
}

---

五、勾股定理

勾股定理，西方称为毕达哥拉斯定理，它所对应的三角形现在称为：直角三角形。

已知直角三角形的斜边是某个整数，并且要求另外两条边也必须是整数。

求满足这个条件的不同直角三角形的个数。

【数据格式】
输入一个整数 n (0 < n< 10000000) 表示直角三角形斜边的长度。
要求输出一个整数，表示满足条件的直角三角形个数。

例如，输入：
5
程序应该输出：
1

再例如，输入：
100
程序应该输出：
2

再例如，输入：
3
程序应该输出：
0

资源约定：
峰值内存消耗（含虚拟机） < 256M
CPU消耗 < 1000ms

请严格按要求输出，不要画蛇添足地打印类似：“请您输入…” 的多余内容。
所有代码放在同一个源文件中，调试通过后，拷贝提交该源码。
注意：不要使用package语句。不要使用jdk1.7及以上版本的特性。
注意：主类的名字必须是：Main，否则按无效代码处理。

import java.util.Scanner;

public class Main {
    static int[] s;
    public static void main(String[] args) {
        Scanner input = new Scanner(System.in);
        int n = input.nextInt();
        int cnt = 0;
        for (int i = 1; i < Math.sqrt(Math.pow(n, 2)/2); i++) {
            int j = (int) Math.sqrt(Math.pow(n, 2) - Math.pow(i, 2));
            if (Math.pow(i, 2) + Math.pow(j, 2) == Math.pow(n, 2)) {
                cnt++;
            }
        }
        System.out.println(cnt);
    }
}

---

六、九阶数独

你一定听说过“数独”游戏。
如【图1.png】，玩家需要根据9×9盘面上的已知数字，推理出所有剩余空格的数字，并满足每一行、每一列、每一个同色九宫内的数字均含1-9，不重复。

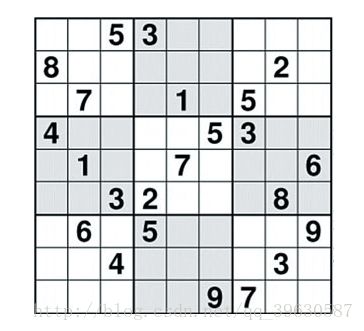
数独的答案都是唯一的，所以，多个解也称为无解。
本图的数字据说是芬兰数学家花了3个月的时间设计出来的较难的题目。但对会使用计算机编程的你来说，恐怕易如反掌了。
本题的要求就是输入数独题目，程序输出数独的唯一解。我们保证所有已知数据的格式都是合法的，并且题目有唯一的解。
格式要求，输入9行，每行9个字符，0代表未知，其它数字为已知。
输出9行，每行9个数字表示数独的解。

例如：
输入（即图中题目）：
005300000
800000020
070010500
400005300
010070006
003200080
060500009
004000030
000009700

程序应该输出：
145327698
839654127
672918543
496185372
218473956
753296481
367542819
984761235
521839764

再例如，输入：
800000000
003600000
070090200
050007000
000045700
000100030
001000068
008500010
090000400

程序应该输出：
812753649
943682175
675491283
154237896
369845721
287169534
521974368
438526917
796318452

资源约定：
峰值内存消耗（含虚拟机） < 256M
CPU消耗 < 2000ms

请严格按要求输出，不要画蛇添足地打印类似：“请您输入…” 的多余内容。
所有代码放在同一个源文件中，调试通过后，拷贝提交该源码。
注意：不要使用package语句。不要使用jdk1.7及以上版本的特性。
注意：主类的名字必须是：Main，否则按无效代码处理。

import java.util.Scanner;

public class Main {
    static String[][] a = new String[9][9];
    public static void main(String[] args) {
        Scanner input = new Scanner(System.in);
        for (int i = 0; i < 9; i++) {
            String[] str = new String[9];
            str[i] = input.nextLine();
            a[i] = str[i].split("");
        }
        backtrace(0, 0);

    }

    private static void backtrace(int x, int y) {
        if (x == 9) {
            for (int i = 0; i < 9; i++) {
                for (int j = 0; j < 9; j++) {
                    System.out.print(a[i][j]);
                }
                System.out.println();
            }
        } else {
            if (a[x][y].equals("0")) {
                for (int i = 1; i <= 9; i++) {
                    a[x][y] = i+"";
                    if(check(x, y)) {
                        if (y + 1 < 9) {
                            backtrace(x, y+1);
                        } else {
                            backtrace(x+1, 0);
                        }
                    }
                    a[x][y] = "0";
                }
            } else {
                if (y + 1 < 9) {
                    backtrace(x, y+1);
                } else {
                    backtrace(x+1, 0);
                }
            }
        }
    }

    private static boolean check(int x, int y) {
        for (int i = 0; i < 9; i++) {
            if (a[x][i].equals(a[x][y]) && i != y) {
                return false;
            }
        }
        for (int i = 0; i < 9; i++) {
            if (a[i][y].equals(a[x][y]) && i != x) {
                return false;
            }
        }
        int row = (x/3)*3;
        int col = (y/3)*3;
        for (int i = row; i < row+3; i++) {
            for (int j = col; j < col+3; j++) {
                if (a[i][j].equals(a[x][y]) && (i!=x || j !=y)) {
                    return false;
                }
            }
        }
        return true;
    }
}

---

七、矩阵射线★★

给定平面内平行于坐标轴的一个矩形，从矩形内选择一些点，从这些点向右和向上各射出一条射线，请问：这些射线将矩形分成了多少份。

数据格式：

输入的第一行包含两个整数x, y，表示矩形是由(0, 0), (x, 0), (x, y), (0, y)四个点围成的。
第二行包含一个整数n，表示矩形内的点的数量。
接下来n行，每个两个整数xi, yi，表示矩形内的一个点。输入保证所有的点都在矩形内部而且没有两个点有相同的横坐标或纵坐标。

输出一个整数，表示从给定的点射出的射线将矩形分成的份数。

例如，输入：
10 10
3
1 3
3 1
2 4
程序应该输出：
6

【数据规模和约定】
对于10%的数据，1<=n<=10，1<=x, y<=100；
对于30%的数据，1<=n<=1000，1<=x,y<=1000；
对于60%的数据，1<=n<=10000，1<=x,y<=1000000；
对于100%的数据，1<=n<=100000，1<=x,y<=1000000000，1 < xi < x，1 < yi < y。

资源约定：
峰值内存消耗（含虚拟机） < 256M
CPU消耗 < 1000ms

请严格按要求输出，不要画蛇添足地打印类似：“请您输入…” 的多余内容。

所有代码放在同一个源文件中，调试通过后，拷贝提交该源码。
注意：不要使用package语句。不要使用jdk1.7及以上版本的特性。
注意：主类的名字必须是：Main，否则按无效代码处理。

解析：这个题目有点涉及计算机图形学的内容，但是只要仔细观察分析，也是能找出规律来的

按照测试用例，我们可以画出如下的图（颜色是丑了点，凑活着看

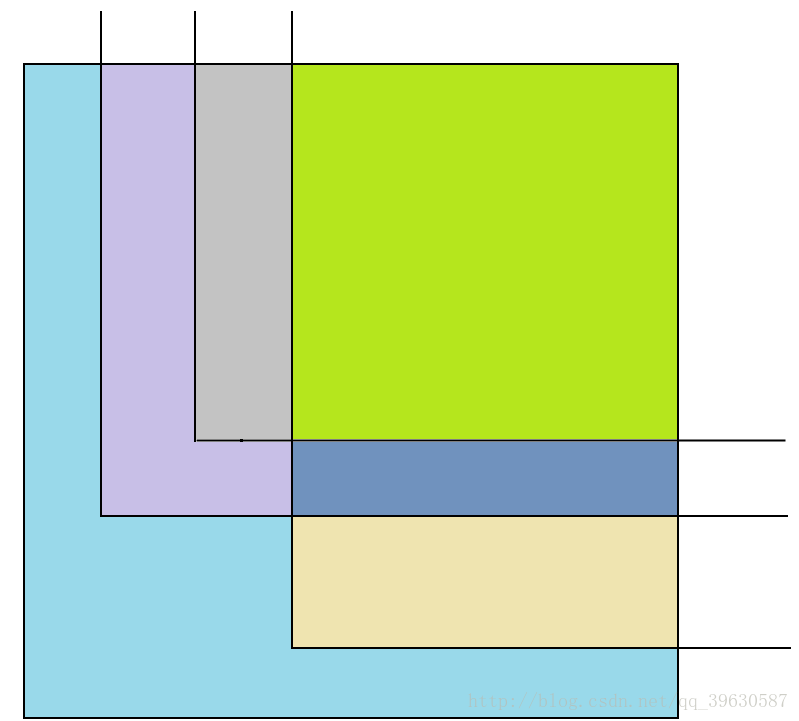
那么如果我们在多加一个点，图中红线延伸出去，我们可以看到这根线与其他的线有两个交点，而两个交点自然就多分出来3个独立的面积，所以答案是6+3=9吧ヽ(￣▽￣)ﾉ），不包含红色那个点，答案就是6

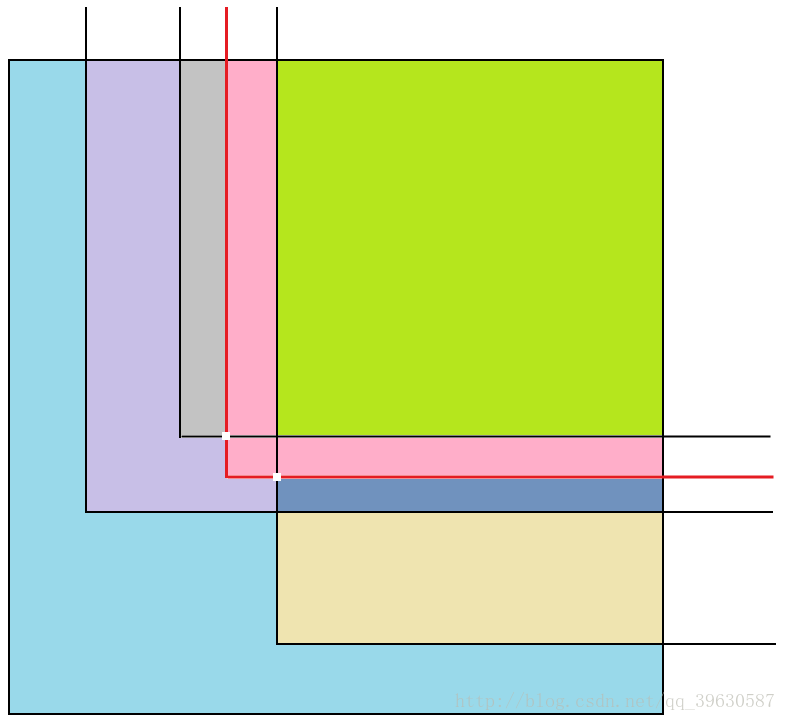
如果还是没有明白的话，下面再加一个点，红线与其他的线有三个交点，所以多出来4个独立的面积

import java.util.*;

public class Main {
    public static long x, y;
    public static int n;
    public static Point[] P;
    public static long count = 1;
    public static ArrayList list = new ArrayList();
    static class Point {
        public int x;
        public int y;

        public Point(int x, int y) {
            this.x = x;
            this.y = y;
        }
    }

    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        x = in.nextLong();
        y = in.nextLong();
        n = in.nextInt();
        /**
         * Point数组，存放n个坐标
         * */
        P = new Point[n];
        for(int i = 0;i < n;i++) {
            int x = in.nextInt();
            int y = in.nextInt();
            P[i] = new Point(x, y);
        }
        getResult();
    }

    public static void getResult() {
        /**
         * 内部类重写Comparator接口，自定义排序
         * */
        Arrays.sort(P, new Comparator() {
            @Override
            public int compare(Point o1, Point o2) {
                if (o1.x >o2.x) {
                    return 1;
                } else if (o1.x < o2.x) {
                    return -1;
                } else if (o1.x == o2.x) {
                    if (o1.y > o1.y) {
                        return 1;
                    } else if (o1.y < o1.y) {
                        return -1;
                    } else {
                        return 0;
                    }
                }
                return 0;
            }
        });
        list.add(P[n - 1].y);
        count++;
        for(int i = n - 2;i >= 0;i--) {
            if(P[i].x == P[i + 1].x) {
                if(P[i].y < P[i + 1].y) {
                    int j = list.indexOf(P[i + 1].y);
                    list.remove(j);
                    list.add(P[i].y);
                }
                /**
                 * 当两个坐标x相等，y由题意可知必定不等，那么必定会分割出一块面积，p[i+1].y > p[i].y 时，更新list数的值
                 * */
                count++;
            }
            else {
                Collections.sort(list);
                int j = 0;
                for(;j < list.size();j++) {
                    if(P[i].y <= list.get(j)) {
                            break;
                    }
                }
                /**
                 * 两条延长线与其他延长线相交x个，那么就会分割出x+1块面积
                 * */
                count += j + 1;
                if (!list.contains(P[i].y)) {
                    list.add(P[i].y);
                }
            }
        }
        System.out.println(count);
    }
}