蓝桥杯Python青少组中/高级国赛真题解析（2023年5月）

第1题
以下选项中，哪一个可以将字典dict1与字典dict2合并？（ ）
A.dict1.add(dict2)
B.dict1.extend(dict2)
C.dict1.update(dict2)
D.dict1.merge(dict2)
【答案】：C
【解析】
字典没有add和extend函数，列表有add和extend函数。
merge是pandas中的内置函数。
字典使用update将两个字典进行合并，故选C。

第2题
执行print(“{1}{0}”.format(“Hello”,“Python”,“!”))语句后，输出的结果是（ ）
A.HelloPython!
B.PythonHello!
C.HelloPython
D.PythonHello
【答案】：D
【解析】
format后的3个变量，分别为变量0、变量1、变量2，所以先打印变量1再打印变量2，为PythonHello，选D。

详情请见：Python format 格式化函数

第3题
关于Python中的全局变量和局部变量，以下选项描述错误的是（ ）
A.全局变量不可以被函数内部的代码块修改
B.全局变量在函数之外一般没有缩进，在程序执行全过程有效
C.全局变量是指在函数之外定义的变量，而局部变量是指在函数内部定义的变量
D.局部变量和全局变量可以共存，但如果局部变量和全局变量的名称相同，局部变量会覆盖全局变量
【答案】：C
【解析】
可以通过global将函数内部定义的变量声明为全局变量，故选C。

详情请见：Python3 命名空间和作用域，全局变量和局部变量

第4题
下列函数中哪一个可以删除集合中指定的元素？（ ）
A.clear()
B.discard()
C.union()
D.issubset()
【答案】：B
【解析】
clear()用于清除集合中所有元素，discard用于删除集合中指定的元素，union用于合并两个集合，issubset用于判断集合y是否为集合x的子集

详情请见：Python 集合

第5题
以下选项中，哪一个可以更好地描述Python中类方法和静态方法之间的区别？（ ）
A.类方法只能由类调用，而静态方法只能由实例调用
B.类方法可以访问类和实例的属性和方法，而静态方法不能访问
C.类方法必须要有一个参数，而静态方法可以没有参数
D.类方法只能访问类的属性和方法，而静态方法只能访问实例的属性和方法
【答案】：
【解析】
类方法也可以由实例调用，A不正确。
类方法只能访问类的属性和方法，不能访问实例的属性和方法，B错误。
静态方法不能调用实例中的属性和方法，D不正确。

class Person:
    sex = "男性"
    def __init__(self,name, age): # 构造函数，实例化的时候自动调用
        self.name = name
        self.age = age
        print(self.name, self.age)

    @classmethod
    def clsMethod(cls):
        print("这是类方法，因为它被classmethod修饰")
        print(cls.sex)
    @staticmethod
    def stMethod():
        print("这是静态方法，因为它被staticmethod修饰")
        # print(cls.sex)  # 静态方式不能调用类中的方法和属性，也不能访问实例的属性和方法

Person.clsMethod() # 使用类名调用类方法
Person.stMethod()  # 使用类名调用静态方法
stu1 = Person("tom", 24)
stu2 = Person("bob", 26)
stu1.clsMethod()  # 使用实例名称调用类方法
stu1.stMethod()  # 使用实例名称调用静态方法

stu1.sex = "女性"
print(stu1.sex)  # 女性 实例化后，可以修改类属性
stu1.clsMethod()  # 男性 类方法只能打印类属性，不能访问实例属性

第6题 统计字母数量

【题目描述】

例如：S=“1Abb”， 其中字母有A， b， b一共有3个。给定一个字符串S（S长度<100） ， 统计字符串中字母一共有多少个。

【输入】

输入一个字符串S（S长度<100）

【输出】

输出一个整数，表示字符串S中字母的个数

【输入样例】

1Abb
1
【输出样例】

3
1
【代码详解】

s = input()
ans = 0
for c in s:
    if c.isalpha():
        ans+=1
print(ans)

【运行结果】

1Abb
3

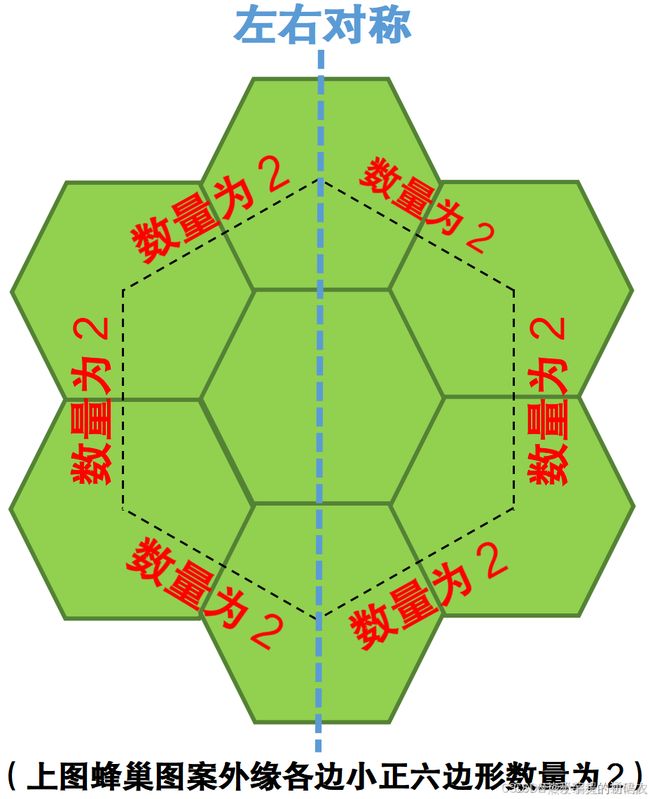
第7题 蜂巢里的蜗牛

【题目描述】
有一个由多个小正六边形组成的蜂巢图案，蜂巢外缘各边的小正六边形数量一致，且左右对称。

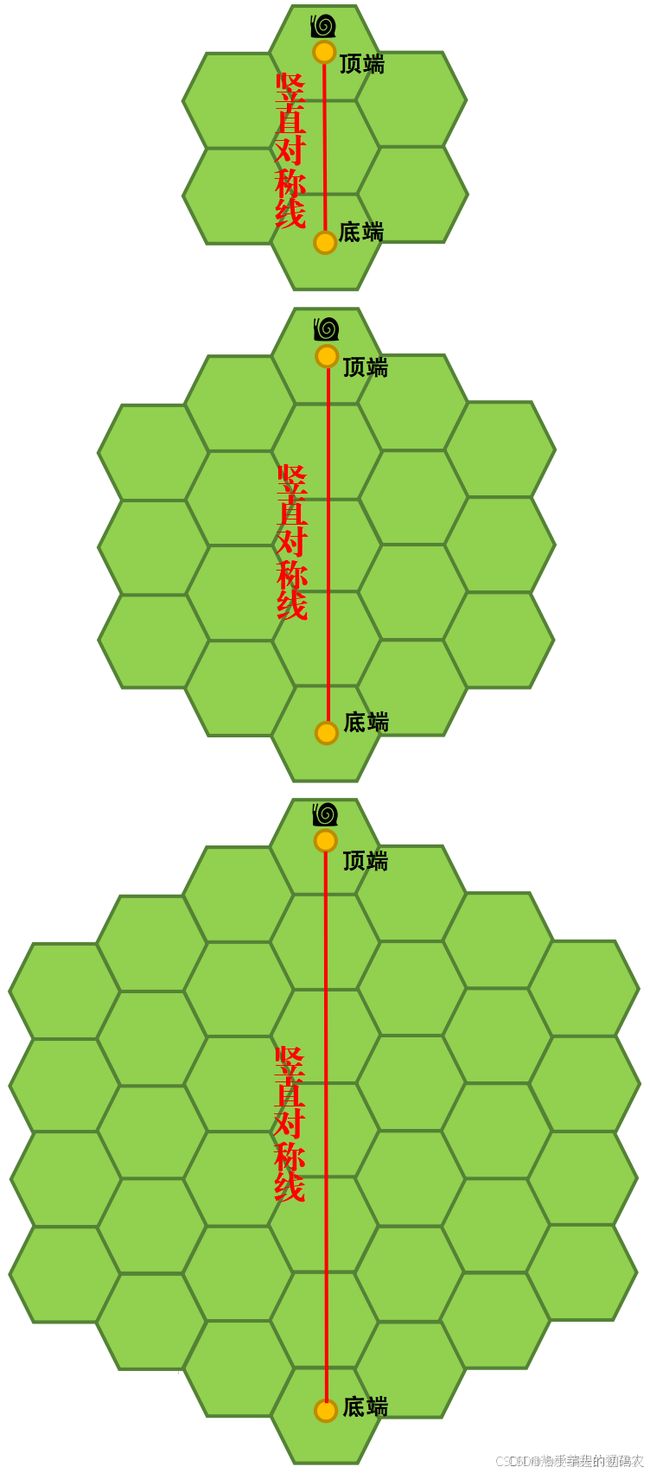
以下为竖直对称线上小正六边形个数为3、5、7的3个蜂巢图案。

编程实现
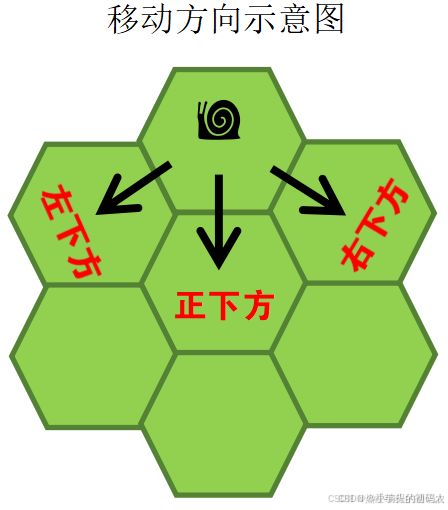
有一只蜗牛要从竖直对称线顶端的小正六边形处移动到底端的小正六边形中，它每次只能向它所在位置的小正六边形的左下方、正下方、右下方相邻的小正六边形处移动。

已知竖直对称线上有N个小正六边形，请计算出蜗牛从竖直对称线顶端移动到底端共有多少条不同的移动路线。
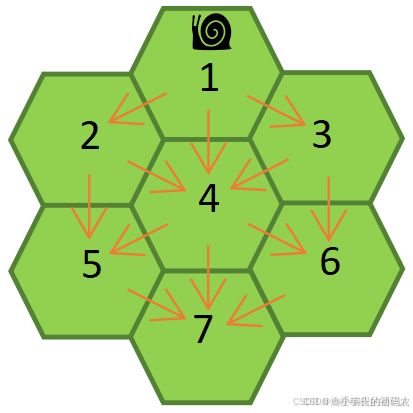
例如：N = 3，竖直对称线上有3个小正六边形，如下图：

蜗牛从竖直对称线顶端的小正六边形处（1号处）移动到另一端的小正六边形中（7号处）共有11条不同的路线。
11条不同的路线分别为：
（1->2->5->7）、（1->2->4->7）、（1->2->4->5->7）、（1->2->4->6->7）、（1->4->5->7）、（1->4->7）、（1->4->6->7）、（1->3->4->5->7）、（1->3->4->7）、（1->3->4->6->7）、（1->3->6->7）。

【输入】

输入一个正整数N（2＜N＜30，N为奇数），表示图案上竖直对称线上小正六边形的个数

【输出】

输出一个整数，表示蜗牛从竖直对称线顶端移动到底端共有多少条不同的移动路线

【输入样例】

3
【输出样例】

11
【代码详解】

row = int(input())
col = row + 2
mid = col // 2
dp = [[0] * col for i in range(row)]
dp[0][mid] = 1

for i in range(1, row):
    for j in range(1, mid):  #左侧
        dp[i][j] = dp[i][j-1] + dp[i-1][j] + dp[i-1][j+1]
    for j in range(col-2, mid, -1):  #右侧
        dp[i][j] = dp[i-1][j-1] + dp[i-1][j] + dp[i][j+1]
    dp[i][mid] = dp[i][mid-1] + dp[i-1][mid] + dp[i][mid+1]  #中间
# print(dp)
print(dp[row-1][mid])

【运行结果】

3
11

第8题 多时段开会

【题目描述】

某公司有多间会议室，可使用时间为8点到22点，同一会议室同一时间段只能由一个部门使用。
一天有N（1≤N≤50）个部门计划使用同一间会议室，且已知每个部门计划使用的开始时间S（8≤S≤21）和结束时间E（S＜E≤22）。请计算出这间会议室最多可以安排多少个部门使用。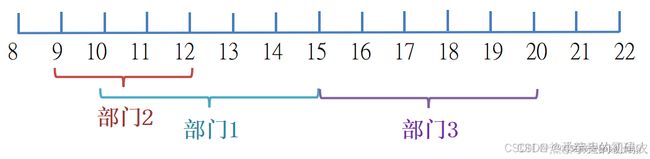

例如：N = 3，3个部门计划使用的开始及结束时间依次为（9，12），（10，15），（15，20）。

10-12点的时间段，部门1和部门2都计划使用，所以只能由一个部门使用；15-20点的时间段，只有部门3计划使用，所以这间会议室最多可以安排2个部门使用（部门1和部门3或者部门2和部门3）。

【输入】

第一行输入一个正整数N（1≤N≤50），表示计划使用同一间会议室的部门数量
接下来输入N行，每行两个正整数S和E（8≤S≤21，S＜E≤22），分别表示某部门计划使用会议室的开始时间和结束时间，正整数之间以一个空格隔开

【输出】

输出一个整数，表示这间会议室最多可以安排多少个部门使用

【输入样例】

3
9 12
10 15
15 20
【输出样例】

2
【代码详解】

n = int(input())
lst = [[int(i) for i in input().split()] for i in range(n)]
count = 1
newLst = sorted(lst, key=lambda x:x[1])
endTime = newLst[0][1]
for i in range(1, len(newLst)):
    if endTime <= newLst[i][0]:
        endTime = newLst[i][1]
        count += 1
print(count)

【运行结果】

3
9 12
10 15
15 20
2

第9题 黑暗料理

【题目描述】

小贝要做一份黑暗料理，现有N（2≤N≤20）种不同的食材供她选择，食材编号从1到N。其中有些食材同时食用会产生副作用，所以产生副作用的食材只能选择其中一种食材或者都不选择。
已知同时食用会产生副作用的食材有M对（0≤M≤N*（N-1）/2），请计算出这份黑暗料理中最多能有多少种食材。
注意：会产生副作用的食材以两个编号表示，两个编号不等且编号小的在前，例如（1，2）和（2，3）。
例如：N=5，M=3时，5种食材编号为1到5，其中有3对食材会产生副作用：（1，2）、（2，3）、（4，5）。
可选择1、3、4号食材或1、3、5号食材做黑暗料理，最多可以有3种食材。

【输入】

第一行输入两个正整数N（2≤N≤20）和M（0≤M≤N*（N-1）/2），分别表示食材数量及会产生副作用的食材对数，两个正整数之间以一个空格隔开
接下来输入M行，每行两个正整数（1≤正整数≤N），表示会产生副作用的两种食材编号，两个正整数之间以一个空格隔开，两个编号不等且编号小的在前

【输出】

输出一个整数，表示这份黑暗料理中最多能有多少种食材

【输入样例】

5 3
1 2
2 3
4 5
【输出样例】

3
【代码详解】

n, m = [int(i) for i in input().split()]
ls = []
for i in range(m):
    ls.append([int(i) for i in input().split()])
# 用来标记对应索引的食材是否取用：0，不取；1，取
use = [0] * n
maxn = 0
def dfs(step):
    global maxn
    if step>=n:
        for i in ls:
            #如果两种食材冲突，那么不符合要求，直接返回
            if use[i[0]-1]==1 and use[i[1]-1]==1:
                return
        maxn = max(sum(use), maxn)
        return 
    # 不取用的情况
    use[step] = 0
    dfs(step+1)
    # 取用的情况
    use[step] = 1
    dfs(step+1)
dfs(0)
print(maxn)

【运行结果】

5 3
1 2
2 3
4 5
3

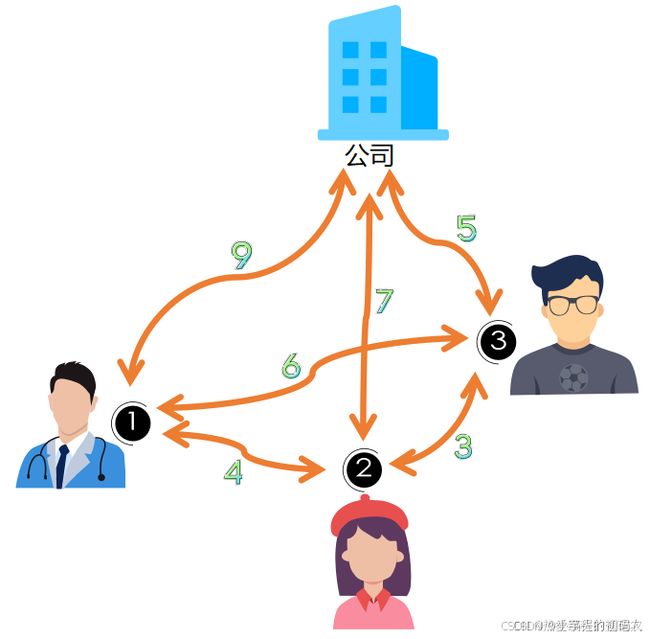
第10题 拜访客户

【题目描述】

小蓝从公司出发，要去拜访N（3≤N≤15）个客户，已知公司到每个客户的路程时间，及N个客户之间的路程时间。请计算出小蓝拜访完所有客户并返回到公司，最少需要多少时间。（道路双向通行，可重复走）
例如：N = 3，有3个客户需要拜访，公司到1号、2号、3号客户的路程时间依次为9，7，5，客户1到客户2和客户3的路程时间依次是4，6，客户2到客户3的路程时间是3。

从公司出发拜访完3名客户并返回公司最少需要的路程时间为21，行走路线为：公司 --> 3号 --> 2号 --> 1号 --> 公司（21=5+3+4+9）。

【输入】

输入描述
第一行输入一个正整数N（3≤N≤15），表示要拜访的客户数量
第二行输入N个正整数（1≤正整数≤1000），依次表示公司到1号~N号客户的路程时间，正整数之间以一个空格隔开
第三行输入N-1个正整数（1≤正整数≤1000），依次表示1号客户到2号~N号客户的路程时间，正整数之间以一个空格隔开
第四行输入N-2个正整数（1≤正整数≤1000），依次表示2号客户到3号~N号客户的路程时间，正整数之间以一个空格隔开
…
第N+1行输入一个正整数（1≤正整数≤1000），表示N-1号客户到N号客户的路程时间

【输出】

输出一个整数，表示小蓝拜访完N名客户并返回公司最少需要的路程时间

【输入样例】

3
9 7 5
4 6
3
【输出样例】

21
【代码详解】

# 该方法只能过3个测试点，2个会TLE
from itertools import permutations
n = int(input())
lstTime = [[0 for i in range(n+1)] for i in range(n+1)]
for i in range(n):
    ls = [int(i) for i in input().split()]
    for j in range(len(ls)):
        lstTime[i][j+i+1] = ls[j]
        lstTime[j+i+1][i] = ls[j]
client = [i for i in range(1, n+1)]
resLst = []
tmpLst = []

arr = [i for i in range(1, n+1)]
minTime = 1000000000
for i in permutations(arr):
    i = list(i)
    i = [0] + i +[0]
    costTime = 0
    for j in range(len(i)-1):
        # print(i[j], i[j+1])
        if i[j]==0:
            costTime += lstTime[i[j]][i[j+1]]
        else:
            costTime += min(lstTime[i[j]][0] + lstTime[0][i[j+1]], lstTime[i[j]][i[j+1]])
    minTime = min(minTime, costTime)
print(minTime)

# AC代码
n = int(input())
ls = []
for i in range(n):
    ls.append([int(i) for i in input().split()])
ls.append([])
n += 1
for i in range(n):
    ls[i] = [0] * (i+1) + ls[i]
for i in range(n):  # 构建去每个客户地点时间的二维列表
    for j in range(n):
        ls[j][i] = ls[i][j]
for k in range(n):  # Floyd算法分析去每个客户地点的最小时间
    for i in range(n):
        for j in range(n):
            ls[i][j] = min(ls[i][j], ls[i][k]+ls[k][j])

# 2^(n-1)为除起点之外的所有自己的数量（二进制表示法）
N = 1 << (n-1)
# dp数组，初始值为正无穷
dp = [[float("inf")] * n for _ in range(N)]
# 边界条件，只有一个起点时，最短路径为0（不包括起点）
for i in range(1, n):
    dp[1<<(i-1)][i] = ls[0][i]

# 状态转移
for S in range(1, N):
    for i in range(1, n):
        if not(S & (1<<(i-1))):
            continue
        for j in range(1, n):
            if i==j or not(S & (1<<(j-1))):
                continue
            dp[S][i] = min(dp[S][i], dp[S^(1<<(i-1))][j] + ls[j][i])

# 计算最短路径（最后回到起点）
ans = float("inf")
for i in range(1, n):
    ans = min(ans, dp[N-1][i] + ls[i][0])
print(ans)

【运行结果】

3
9 7 5
4 6
3
21

第11题 数字合并

【题目描述】

有一组正整数数据，现对这组数据按照如下操作：
1）从这组数中找出两个相邻且相同的数，删掉其中一个数，剩下的一个数加1（例如：两个相邻的6，变成一个7）；
2）重复操作第1步，直到这组数据中没有相邻且相同的数时，操作结束。
现给定N（1≤N≤2000）个正整数，表示这一组数，请问按照要求操作结束后，这组数据中最大的数是多少。
注意：不同的操作方式得到的最后结果不同，要求最后的结果是所有操作方式中最大的。
例如：
当N=6，这组数为 1、2、2、2、3、4时，
可获得最大结果的操作如下：
第一次操作：将这组数据中后两个相邻的2，变成3，此时这组数变为1，2，3，3，4；
第二次操作：将这组数据中两个相邻的3，变成4，此时这组数变为1，2，4，4；
第三次操作：将这组数据中两个相邻的4，变成5，此时这组数变为1，2，5；
此时这组数据中没有相邻且相同的数，操作结束，最大的数是5。
非最大结果的操作如下：
第一次操作：将这组数据中前两个相邻的2，变成3，此时这组数变为1，3，2，3，4；
此时这组数据中没有相邻且相同的数，操作结束，最大的数是4。
所以按照要求操作结束后，这组数据中可获得的最大数是5。

【输入】

第一行输入一个正整数N（1≤N≤2000）
第二行输入N个正整数（1≤正整数≤40），相邻两个数之间以一个空格隔开

【输出】

输出一个正整数，表示所有操作方式中最大的结果

【输入样例】

6
1 2 2 2 3 4
【输出样例】

5
【代码详解】

# 该代码只能过3个测试点，2个会TLE
import sys
sys.setrecursionlimit(100000)
n = int(input())
lst = [int(i) for i in input().split()]

def dfs(lst, maxNum):
    for i in range(len(lst)-1):
        if lst[i] == lst[i+1]:
            tmpLst = lst[:i] + [lst[i]+1] + lst[i+1:]
            tmpLst.pop(i+1)
            maxNum = dfs(tmpLst, maxNum)
            maxNum = max(maxNum, max(tmpLst))
    return maxNum

res = dfs(lst, 0)
print(res)

n = int(input())
ls = [int(i) for i in input().split()]
f = [[0] * (2002) for i in range(51)]
for i in range(1, n+1):
    f[ls[i-1]][i] = i+1
ans = 0
for i in range(2, 51):
    for j in range(1, n+1):
        if f[i][j] == 0:
            f[i][j] = f[i-1][f[i-1][j]]
        if f[i][j]:
            ans = i
print(ans)

【运行结果】

6
1 2 2 2 3 4
5

转载自：历年蓝桥杯Python青少组中/高级国赛省赛真题解析 | 2023年5月（国赛）选择题（1-5）历年蓝桥杯Python青少组中/高级国赛省赛真题解析 | 2023年5月（国赛）编程题（6-11）