《编译原理》画 DAG 图与求优化后的 4 元式代码- 例题解析
《编译原理》画 DAG 图与求优化后的 4 元式代码- 例题解析
DAG 图(Directed Acylic Graph)无环路有向图
(一)基本块
基本块是指程序中一顺序执行的语句序列,其中只有一个入口语句(第一个语句)和一个出口语句(最后一个语句)
对于一个基本块来说,执行时只能从其入口语句进入,从其出口语句退出
| 语句 | |
|---|---|
| 出口语句 | 任何控制转移四元式 |
| 入口语句 | 所转向的目标语句 |
(二)划分基本块的步骤
1、求四元式序列中各个基本块的入口语句。
- ① 程序的第一个语句
- ② 能由条件或无条件转移语句转移到的语句
- ③ 紧跟在条件转移语句后面的语句
2、对每一入口语句,构造所属的基本块,该基本块由:
- 1)该入口语句到下一入口语句(不包括下一入口语句)之间的语句序列组成
- 2)该入口语句到一转移语句(包括该转移语句)之间的语句序列组成
- 3)该入口语句到一停语句(包括该停语句)之间的语句序列组成
3、凡是未包含在某一基本块中的语句,都是程序中控制流程不可达的语句,可删除它们。
例题:
对于下面给出的求最大公因子的程序,可以根据基本块的构造规则与其划分基本块
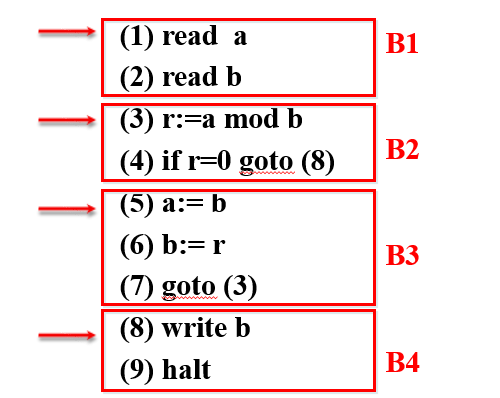
基本块构造步骤:
(1):由规则 (1) 中的 ① 可知语句 (1) 是一个入口语句
(2):由规则 (1) 中的 ② 可知,语句 (3) 和 (8) 均是人口语句
(3):由规则 (1) 中的 ③ 可知,语句 (5) 是二个人口语句,可以用 “+” 在人口语句的左侧作标记。
(4):由规则 (2) 可以划分该程序为四个基本块,它们分别是:
- 语句 (1)、(2) 组成的基本块 B1
- 语句 (3)、(4) 组成的基本块 B2
- 语句 (5)、(6) 和 (7) 组成的基本块 B3
- 语句 (8) .(9) 组成的基本块 B4
程序中在代码段左侧对各个基本块进行了标记。
(三)程序控制流程流图
定义: 以基本块为结点,控制程序流向作为有向边,画出的有向图称为流图。
特点:
- 具有唯一首结点的有向图
- 从首结点开始到流图中任何结点都有通路
如果一个结点的基本块的入口语句是程序的第一条语句,则称此结点为首结点
程序控制流程流图的表示
一个控制流程图可表示成一个三元组:
G=(N,E,n0 )
N:所有结点(基本块)集;
E:所有有向边集;
n0 :首结点。
有向边:
当下述条件有一个成立时,从结点i有一有向边引向结点 j:
- ① 基本块 j 在程序的位置紧跟在i后,且 i 的出口语句不是无条件转移或停语句
- ② i 的出口是 goto(S) 或 if goto(S),而 (S) 是 j 的入口语句
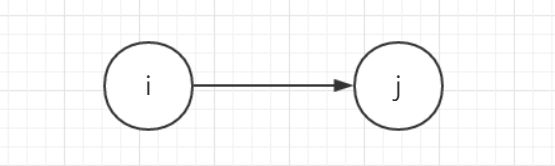
构造程序控制流图
对程序基本块:

构造以下程序控制流图:
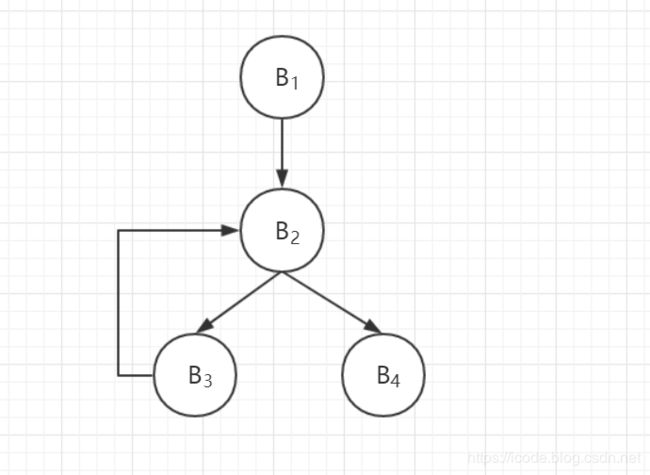
(四)基本块的 DAG 表示
DAG Directed Acyclic Graph 无环路有向图
定义:
(1) 在一个有向图中,若结点 ni 有弧指向结点 nj,则 ni 是 nj 的父结点,nj 是 ni 的子结点;
(2) 若 n1,n2,…,nk 间存在有向弧 n1→n2→…→nk,则称 n1 到 nk 之间存在一条通路,若有 nk=n1,则称该通路为环路;
(3) 若有向图中任意通路都不是环路,则称该图为无环路有向图(DAG)
用来描述基本块的 DAG:
(1) 图的叶结点以一标识符或常数做标记,表示该结点代表该变量或常数的值。
(2) 图的内部结点以一运算符作为标记;
(3) 图中各个结点上可能附加一个或多个标识符,表示这些标识符具有该结点所代表的值,简称附标。
四元式对应的 DAG 结点形式
按其四元式对应结点的后继个数分成四种类型:0型、1型、2型、3型
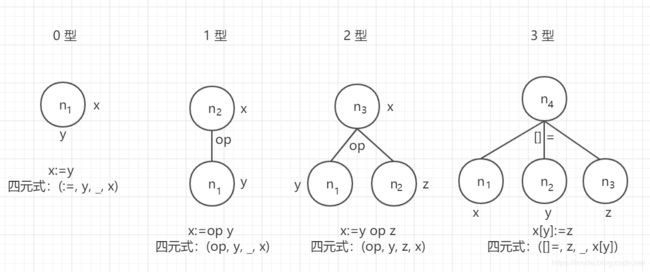
(五)DAG 图构造例题
对于基本块 P
(1)S0 := 2
(2)S4 := 2
(3)S1 := 1.5
(4)S2 := T-C
(5)S3 := T+C
(6)S5 := S3
(7)R := 2/S3
(8)S6 := R
(9)H := R*S2
(1)试用 DAG 进行优化并重写基本块
(2)假定只有 R,H 在基本块出口是活跃的,试写出优化后的 4 元式序列
(只需要还原活跃变量)
解析:
(1)画出 DAG 图如下:
画图的步骤就是:根据基本块,一部一部组装
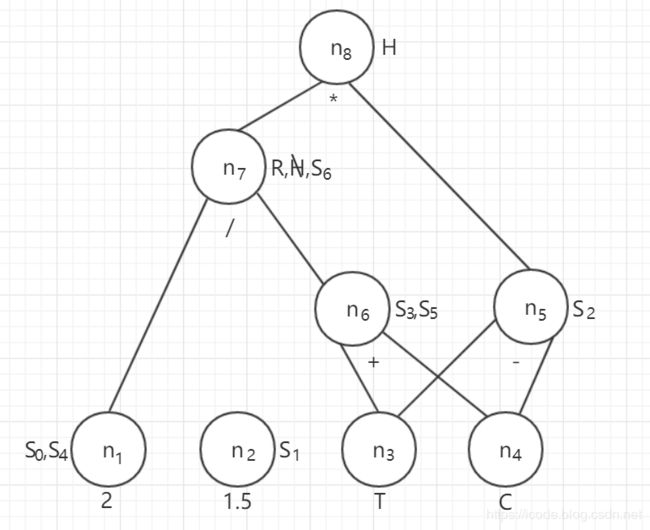
(2)假定只有 R,H 在基本块出口是活跃的,试写出优化后的 4 元式序列
(只需要还原活跃变量)
优化后的 4 元式代码可以写为:
(1)S2 := T-C
(2)S3 := T+C
(3)R := 2/S3
(4)H := R*S2
解释:
与原来的基本块相比较可以看出:
- 原基本块中的 (2) 和 (7) 中的已知量都已经合并。因为 (2) 中 S4 := 2,(7) 中用 2,所以合并。
- (5) 和 (8) 中的公共子表达式 T+C 只在 (5) 中计算一次,在 (8) 中 直接引用其结果,所以删除了多余运算。
- (6) 中的无用赋值已被删除。S5 := S3,S5 后面没有再用,所以就和 S3 一起表示。
除了可以应用 DAG 进行上述的优化外,还可以从基本块的 DAG 中得到一些其他信息:
- DAG 叶结点上标记的标识符是在该基本块之前的基本块内被定值,并在该基本块内被引用的标识符。
- DAG 各结点上的附加标识符是在基本块内被定值,并可以在基本块后被引用的标识符。
如果确认某结点的一个附加标记在基本块后不会被引用,则该标识符的定值语句可以作为死代码被删除。
假设上面例子中 S0~S6。在基本块后面都不会被引用只有 R, H 在基本块出口是活跃的则优化后的四元式序列可以写为:
(1)S2 := T-C
(2)S3 := T+C
(3)R := 2/S3
(4)H := R*S2