图算法与复杂网络

笔者最近一直在研究图算法，在研究图算法前，对复杂网络分析进行了研究，笔者的上篇博文就是对研究的复杂网络分析的内容进行的总结。图算法，字面意思上看，就是对图进行处理的算法。在学习前，笔者一直有个疑问，图究竟属不属于复杂网络？再学习了如下两本书中的内容后，笔者还是没有得到准确的答案。

注：本书部分内容及观点总结自以下书籍：
1.《Graph Algorithms》Mark Needham, Amy E.Hodler著，2019年5月版；
2.《Spark GraphX》Micheal S.Malak, Robin East著，2017年4月版；
3.《复杂网络算法与应用》孙玺菁,司守奎 著，2015年6月版。

在图算范与复杂网络分析的书中，笔者学习到了很多内容相似甚至相同的处理算法，如中心性计算，路经查询等，包括复杂点的社团结构。那么，二者之间到底是什么关系？笔者个人认为，重要的事情说n遍，仅限作者个人意见，…，仅限作者个人意见，笔者认为图算法应该属于复杂网络分析中的一种特殊情况，而复杂网络分析并不是仅有图算法内容。

下面笔者简单对基本图算法进行总结：
1路径寻找
路径寻找算法建立在图寻找算法之上，为了寻找两个节点间的最优路径。路径寻找算法包括最短路径、到所有点最短路径和单资源最短路径、最小生成树、随机游走。
1.1最短路径
加权最短路径
输入：起始节点、终止节点
输出：最短路径长度
遍历方法：
1）广度优先寻找：先遍历节点直接相连的节点，遍历完成后再遍历相邻节点直接相连的节点，以此类推。
2）深度优先寻找：首先遍历节点相连的点，当遍历到该节点时，若该节点有其他相连节点，则继续遍历相邻节点，不需要折返。

1.2全节点对最短路径
1.2.1到所有点最短路径
输入：起始节点
输出：从起始节点到图其他节点的最短路径
算法步骤：
1）设定节点到本节点的距离为无穷大；计算并记录从起始节点经一跳可到达的节点及其路径权值；
2）计算从起始节点经两跳可到达的节点及其路径权值和，与步骤1）中结果对比，若相同起始节点，路径权值和小于步骤1）中的，则更新权值路径；
3）重复步骤2），可得出最终起始节点到全图各节点的最短路径。

1.2.2单资源最短路径
输入：起始节点
输出：从起始节点到其他各节点的最短路径
算法步骤：
1）从起始节点开始，首先选择路径权值最小的边连接的节点；
2）再从起始节点开始计算，选择到达路径权值最小的节点；
3）不断重复步骤2），直到遍历完所有节点。

1.3最小生成树
输入：起始节点
输出：由起始节点构建的最小生成树
算法步骤：
1）从起始节点开始，选择边权值最小的点，将被选中的节点添加到树中；
2）重复选择边权值最小的点，当没有新的节点被添加入生成树的时候，算法介数。
注：单资源算法和最小生成树算法的区别：单资源算法每次计算的是从根节点开始路径权值的总和，而最小生成树仅仅看下一步的权值。

2中心性计算
2.1度中心性
节点的出边个数称为出度，入边个数称为入度。
2.2紧密中心性
紧密中心性标准化方程：

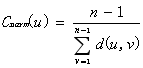
其中，u为节点，n为图中节点的个数，d(u,v)为节点v与节点u之间的最短距离。为了解决无连接图的干扰，引入调和中心性，其标准方程如下：

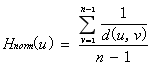
2.3介数中心性
介数中心性计算公式如下：

其中，u为节点，p为节点s与节点t之间最短路径的个数，p(u)为节点s与节点t之间经过节点u的最短路径的个数。

2.4 PageRank
PageRank计算公式如下所示：

其中，我们假设u页有从T1页到Tn页的引文;d是取值为0至1之间的抑制参数，常设置为0.85；1-d表示不遵循任何关系直接到达节点的可能性；C(Tn)表示节点T的出度。

3社团检测算法
3.1三角计数和聚类系数用于分析总体关系密度
测量节点产生三角计数和度的多少，为了决定哪些节点倾向于聚集在一起。
节点u的聚类系数计算公式如下：

其中，u表示节点；R(u)表示通过u的三角计数；k(u)表示节点u的度。
聚类系数能够使我们快速的找到明显的小团体。

3.2强连通组件和连通组件用于找到连接的群集
强连通组件：查找可以从同一组中的每个其他节点按照关系的方向访问每个节点的组；
连通组件：查找可以从同一组中的每个其他节点访问每个节点的组，而不考虑关系的方向。

3.3标签传递为了根据节点标签快速推断团体
根据多数相邻节点，以标签传递的方式推断团体，是一个快速寻找社团的方法。
标签传递算法：
输入：带标签的节点
输出：不同标签种类的社团
算法步骤：
1）首先确定带有标签的节点；
2）将与标签节点直接相连的节点打上其对应的标签；
3）最近标记的节点被激活，变为新的标签节点，重复步骤2）；
4）当遇到两不同标签节点都准备激活同一节点时，可根据设定关系（如根据边权值的大小）进行决定选择；
5）标签传递结束。
注：标签传递算法每次运行的结果都可能不一样，因为初始节点的选择可能不同。

3.4 Louvain模块化为了查看团体质量和层次结构
通过将关系权重和密度与定义的估计值或平均值进行比较，使团体的设定精确度最大化。
一个团体的模块系数计算公式如下：

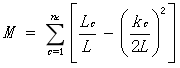
其中，L表示全团体的关系数量；Lc表示分隔中的关系的数量；kc表示分隔中所有节点的度值和。模块度的计算公式如下：

其中，u和v表示节点；m表示总的关系权重；Auv是节点u和v之间关系的权值；ku、kv分别是节点u和v关系权重的总和；最后类似激活函数一样的式子表示节点u、v是否在同一社团，若在同一社团，则其值为1，若不在，则为0。

Louvain模块化算法：
输入：节点个数及节点间的权值，及节点是否在同一社团
输出：最优化的子图模块
算法步骤：
1）将图中的每个节点看成一个独立的社区，社区的数目与节点个数相同；
2）对每个节点u，依次尝试把节点u分配到其每个邻居节点所在的社区，计算分配前与分配后的模块度变化Delta Q，并记录Delta Q最大的那个邻居节点，如果maxDelta Q>0，则把节点u分配Delta Q最大的那个邻居节点所在的社区，否则保持不变；
3）重复2），直到所有节点的所属社区不再变化；
4）对图进行压缩，将所有在同一个社区的节点压缩成一个新节点，社区内节点之间的边的权重转化为新节点的环的权重，社区间的边权重转化为新节点间的边权重；
5）重复1）直到整个图的模块度不再发生变化。

注：常见图算法工具NetworkX包，Spark GraphX,Neo4j等。