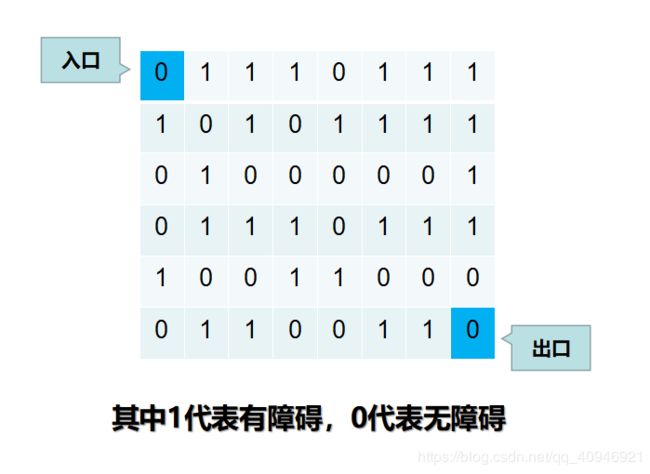
迷宫问题（dfs and bfs）

迷宫问题的求解是实验心理学的一个经典问题.，心理学家把一只老鼠从一个无顶盖的大盒子的入口赶进迷宫，迷宫中设置很多壁障，对前进方向形成了多处障碍，心理学家在迷宫的唯一出口放置了奶酪，吸引老鼠在迷宫中寻找通路以到达出口。设计回溯算法实现迷宫求解。 

 

#include
#include
#include
using namespace std;
vector> mp;
vector> result,minRoad;
int row,col,mycount=0;
int mov[8][2]={{1,1},{1,0},{0,1},{1,-1},{-1,1},{0,-1},{-1,0},{-1,-1}};
void print(vector>& vc){
	for(int i=0;i=0&&a=0&&b> q;
	q.push(make_pair(0,0));
	mp[0][0]=1;
	while(true){
		pair& k=q.front();
		for(int i=0;i<8;i++){
			int a=k.first+mov[i][0],b=k.second+mov[i][1];
			if(a>=0&&a=0&&b>  root = { 
		{0,1,1,1,0,1,1,1},
		{1,0,1,0,1,1,1,1},
		{0,1,0,0,0,0,0,1},
		{0,1,1,1,0,1,1,1},
		{1,0,0,1,1,0,0,0},
		{0,1,1,0,0,1,1,0}								
	};
	row = root.size(); col = root[0].size();
	mp=root;
	mp[0][0]=1;
	result.push_back(make_pair(0,0));
	dfs(0,0);
	mp=root;
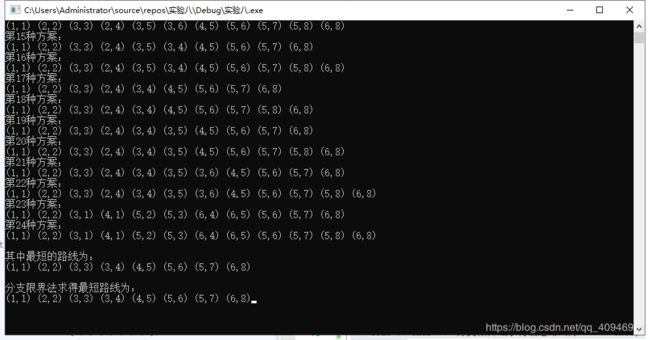
	cout << endl << "其中最短的路线为：" << endl;
	print(minRoad);
	cout << endl << "分支限界法求得最短路线为：" << endl;
	bfs();
	return 0;
}