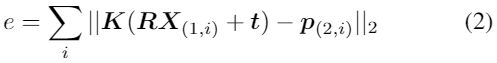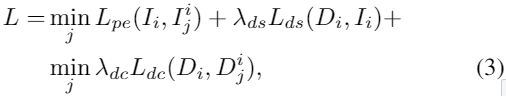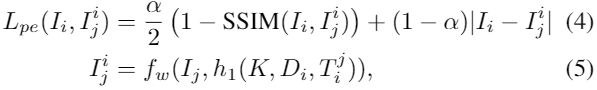Visual Odometry Revisited: What Should Be Learnt?（2020.2）
代码：https://github.com/Huangying-Zhan/DF-VO
文章：https://arxiv.org/abs/1909.09803
摘要
本文利用几何关系和深度学习提出单目视觉里程计（VO）算法。大多数现存的VO/SLAM系统依赖于几何并使用不同传感器，并且大多数单目系统都存在尺度偏移问题。我们使用对极几何以及PNP（Perspective-n-Point）方法处理。使用两个CNN估计单张图像深度和两个光流图作为中间输入，设计了帧到帧的VO算法DF-VO。我们的方法由于使用尺度统一的深度网络，因此不存在尺度漂移。
介绍
基于视觉的定位和建图由于低损耗、低需求是不错选择，并为IMU,GPS,laser等提供信息。VO对于计算机器人相对于前一状态的6D pose很有用。SLAM则对于准确建立机器人轨迹以及对场景建图很重要，并且slam包含回环检测，当轨迹丢失时对机器人重新定位并重新返回同一场景。VO是SLAM进行帧间跟踪的必要部分，精确的里程计会减少定位的总体漂移，并最大程度地减少闭环和全局优化相机轨迹的需求
纯多目几何的VO在合适条件下更准确，如充分的光照、纹理会产生充分的连续帧间的遮挡，当大部分场景是固定的（少量移动物体）。准确估计每帧图像的偏移(translation)尺度对于单目VO/SLAM十分必要，要解决尺度偏移问题就要对map-frame跟踪计算出一个尺度一致图，应用全局bundle adjustment进行尺度优化，或利用例如已知固定相机高度的额外先验。大多数单目图像的depth-translation存在尺度模糊问题，因此估计（结果和运动）结果需要尺度统一。
最近提出了基于深度学习从视频中端到端的学习相机运动[4]–[8]，以及从单张图像估计相应位姿[9]-[11]。并且有的使用网络来预测真世界的尺度，尽管这些方法能够在复杂环境进行相机追踪、定位，但是不能提供有效的几何信息。如图1，比较了本方法的深度学习和几何方法
图1：输入和CNN输出，（a,b）是t与t-1时刻的单目图像输入，并使用自动2D-2D匹配（c）单目深度估计（d,e）前向后向光流估计（f）关于（d,e）前后向光流一致性
2. 相关工作
基于VO的几何： 对于解决VO/SLAM两个主要方法是特征匹配和直接法，前者估计明显的相关性，后者利用最小化重建损失。 对VO的深度学习： Agrawal. [24]从自运动估计学习到视觉特征。Wang[25]提出循环网络从视频中学习。Ummenhofer [26] Zhou [27] 将深度和VO一起学习。Dharmasiri [28] 训练一个深度网络，并用此估计光流和相机运动。 近期工作都以自监督方法学习光度差来代替ground-truth。SfM-Learner [4] 第一个使用自监督估计相机运动和深度。SCSfM-Learner [8]利用深度一致性解决了sfm-learner中的尺度不一致性。之前的UnDeepVO [29] 和Depth-VOFeat [5]使用双目序列解决尺度模糊和不一致问题。
上述问题没有考虑由于计算过程中相机运动而引入的多视图几何约束。CNN-SLAM [30]使用融合单目深度到SLAM系统，CNN-SVO [31]使用CNN提供的深度来初始化特征位置的深度，以减少初始图的不确定性。Yang [32]将深度估计喂入DSO[19]作为虚拟双目计算。Li[33]通过pose-graph优化改进了位姿估计。
3.DF-VO: Depth and Flow for Visual Odometry
本节，使用传统位姿估计方法（对极几何、PNP），如Alg.1
算法： 1. 初始化T为单位矩阵；2. 遍历所有图像；3. 估计 深度及前后光流；4.计算前后光流不一致性；5.从光流中选出高匹配的N对P；6. 如果光流F大于一定阈值；7.从P中恢复|R,t|；8.利用三角关系求解D；9.通过比较估计的D和三角关系计算的D，估计出尺度因子；10.重置T；11.如果不在阈值范围内；12.从（D,F）中建立3D-2D；13.利用PNP估计R，t；14.不计算尺度，直接令T=[R,t]；15. end if；16.迭代计算T
A 传统视觉里程计（VO）
（a）对极几何：
给定图像
,估计相机相对位姿的基本方法是解决基础或本质矩阵E。当建立2D-2D像素
关系后，利用对及约束求解本质矩阵，然后求出相对位姿
【34-37】
2D-2D像素关系由图像中静态像素之间进行提取和匹配，或由光流图计算得到而对于本质矩阵求解存在以下问题：
- 尺度模糊：从本质矩阵恢复出的偏移（translation）up-to-scale
- 纯旋转问题：如果相机只进行旋转无法解出R
- 不稳定结果：如果相机位移过小，结果不稳定
（b）PnP：
Perspective-n-Point (PnP)用来解决3D-2D关系。假设已知场景1中观察到的3D点以及场景2中的投影点
，PnP通过最小化投影损失求解相机位姿 。
为了建立3D-2D关系，使用（1）估计3D场景结构，（2）通过匹配特征，将3D点与2D点进行匹配
B Deep Predictions for Correspondence
假设有两个模型，
和
，分别估计单帧图像深度和两图之间光流。给定一对图像
，用于估计稠密光流，并找到2D-2D关系。然而，估计的光流不是对所有像素都准确，2D-2D对应关系的准确性对于估算准确相对位姿非常重要。为了过滤出光流边缘，估计了前后光流
并使用前后一致性
作为选择高匹配的衡量标准。利用一致度
最高的结果构成N组 2D-2D匹配，
来估计相对位姿。
- 传统特征方法：从局部区域获得视觉信息
- CNN方法：获得更多视觉信息（更大相关区域），高级内容信息，更准确鲁棒高
我们还可以使用估计的深度来进一步估计3D结构，已知2D-2D匹配以及 view-i的3D位置，可以建立起3D-2D关系
C Deep Predictions for Visual Odometry
给定估计深度
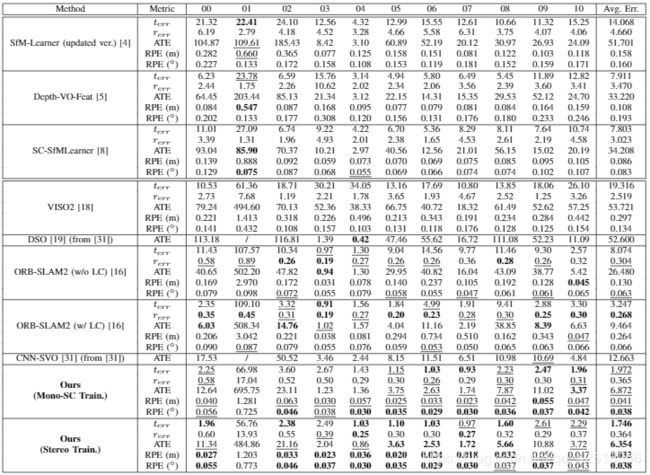
，匹配点
，相对位姿可以通过本质矩阵（2D-2D）或PnP（3D-2D）估计。但如Table2，目前的单目深度估计不能准确估计3D结构。
此外，光流估计比较普遍，且目前的深度学习方法准确。因此，使用2D-2D匹配的方法计算本质矩阵，并用来恢复相机运动。但从两帧图像计算本质矩阵存在一些问题，我们则利用估计的深度结果来解决。
（a）尺度模糊：
从本质矩阵恢复的translation尺度是不确定的。然而，我们使用
作为尺度恢复的参考。首先
从本质矩阵中计算出来。然后，对
使用三角化算出带尺度的深度
，通过比较
估计尺度因子
（b）无解/不稳定问题：
纯旋转造成的病态条件而无法求解本质矩阵。为了解决这两个问题，使用了两个条件检验。
- 平均光流大小（magnitude）：只在平均光流值大于阈值
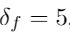时计算本质矩阵，防止小光流造成的小相机运动。 - 测试cheirality条件：对于从
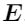中分解的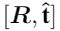
有四种结果，为了找到正确唯一解，三角化的3D点必须同时在相机前面。我们利用其他满足cheirality条件的点，作为结果是否稳定的参考。 如果不满足以上条件，则利用3D-2D的PnP关系来估计相机运动。为了增加鲁棒性，将本质矩阵估计、尺度因子估计、PnP在RANSAC循环中进行（专门用于误匹配）
4 CNN训练网络
A.单目深度估计网络
依赖于数据（monocular/stereo videos, ground truth depths）的不同，训练的网络模型也不同。本文，使用带有skip-connection的encoder-decoder。最简单的方法是用ground-truth的监督方法。近期的自监督方法使用photometric一致度作为监督信号。 按照monodepth2使用单目或双目序列训练，并添加pose网络来最小化下列损失函数（光度差，平滑度差，重投影误差）
为权重，
是对应图像
与从
合成的图像
之间的光度差。其中
是Ii的周围图像，s代表双目对（如果双目训练）。如monodepth2中，不是对连续三帧图像的两两之间的光度差进行均值处理，而是进行取最小值来解决像素移出或遮挡问题
其中
，
是变换函数，
是估计的深度和位姿，
是从view-i到view-j的重投影
是正则化的边缘深度平滑度
尺度模糊和尺度不一致性问题仍然存在单目3D重建中。由于单目局部图像片段训练，不能保证对所有片段使用的是一致尺度从而造成尺度一致性问题。
我们解决的办法是使用双目序列进行训练，根据已知的双目相机基线，估计出具有真实世界尺度且尺度一致的深度。即使双目序列仅使用在训练时候，测试只需单目图像。
另一种解决办法，使用【49】【8】中的当前几何一致性正则化（temporal geometry consistency regularization），限制了多图像间深度一致性。由于使用相机在固定场景的假设，我们希望view-i的深度与view-j的一致，这通过对将frame-j向frame-i进行场景几何正确变换（correctly transforming），类似于图像变换。并采用了mono中的逆深度一致性
深度一致性在三帧图像的两两间取最小值，而不是平均值
B. 光流网络
本文选用LiteFlowNet [52]作为。LiteFlowNet是一个双流网络，分别用来特征提取以及一个进行流计算和正则化的级联网络。即使LiteFlowNet由合成数据训练，对真实数据仍然有效。我们展示了自监督网络利用光流能够更好的应用于没看到的环境，光流网络用来最小化以下函数平均值
与Eqn.5 不同，
使用光流对view-i和view-j建立相关性，我们还是用
加强光流平滑度，与Meister【54】相似，我们估计了前后方向的光流并使用
加强双向（bidirectional）估计的一致性
