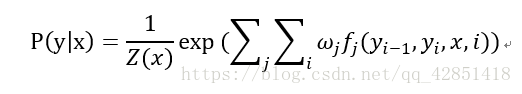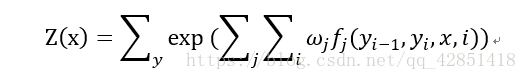命名实体识别

命名实体识别

1. 概念

NER 是 NLP 中一项基本任务，就是从文本中识别出命名性指称项，为关系抽取等任务做铺垫，在信息抽取、信息检索、机器翻译、问答系统等多种自然语言处理技术中必不可少的组成部分。

命名实体识别研究的命名实体一般分为 3 大类（实体类、时间类、数字类）和 7 小类（人名、地名、组织机构名、时间、日期、货币和百分比）。由于时间、日期、货币等实体构成的规律比较明显，其实体类型识别通常可以采用模式匹配的方式获得比较好的识别效果，所以，相较而言，人名、地名、机构名较复杂，目前的研究主要以这几种实体为主。

2. 中文命名实体识别

NER 的效果评判主要是看实体的边界是否划分正确以及实体的类型是否标注正确。相对于英文 NER ，中文 NER 有以下难点：
（1）不像英文有明显的实体边界；
（2）各类命名实体的数量众多。如人名大多属于未登录词；
（3）命名实体的构成规律复杂。如中文人名识别可以细分为中国人名识别、音译人名识别等；另外，机构名的组成方式最复杂，种类繁多，规律不统一。
（4）嵌套情况复杂。如人名中嵌套着地名，地名中嵌套着人名、机构名。
（5）长度不确定。相对于人名、地方，机构名的长度和边界更难以识别，中国人名一般为2-4字，常用地方也大多为2-4字，但机构名长度变化范围极大。

3. 命名实体识别的主要三种方法：

1. 基于规则的命名实体识别：
   利用手工构造规则模板，选用特征包括统计信息、标点符号、关键字、指示词和方向词、位置词（如尾字）、中心词等方法，结合命名实体库，对每条规则进行权重赋值，然后通过实体与规则的相符情况来进行类型判断，即：将文本与规则进行匹配来识别出命名实体。例如，对于中文来说，“说”、“老师”等词语可作为人名的下文，“大学”、“医院”等词语可以作为组织机构名的结尾，还可以利用到词性、句法信息。
   当提取的规则能够较好地反映语言现象时，该方法能明显优于其他方法。但在大多数场景下，在构建规则的过程中往往需要大量的语言学知识，不同语言的识别规则不尽相同。规则的构建往往依赖于具体语言、领域和文本风格，其构建规则过程耗时且难以覆盖所有的语言现象，可移植性差、更新维护困难等。

2. 基于统计的命名实体识别：
   目前常用的基于统计机器学习的命名实体识别方法有：隐马尔可夫模型（HMM）、最大熵模型（ME）、支持向量机（SVM）、条件随机场（CRF）等。其主要思想是：基于人工标注的大量语料，将命名实体识别作为序列标注问题，利用语料来学习标注模型，从而对句子的各个位置进行标注。

3. 混合方法：
   自然语言处理并不完全是一个随机的过程，单独使用基于规则的方法，状态搜索空间大，必须要借助规则提前进行过滤修剪处理。目前没有单独使用统计模型而不使用规则知识的命名实体识别系统，很多情况下是使用规则和统计结合的混合方法。

   目前主流的方法是序列标注方式，即特征模板 +CRF 。

4. 基于条件随机场的命名实体识别

条件随机场其主要思想来源于 HMM，也是一种用来标记和切分序列化数据的统计模型。不同的是，CRF 是在给定观察的标记序列下，计算整个标记序列的联合概率，而 HMM 是在给定当前状态下，定义下一个状态的分布。

【 HMM 将分词作为字标注问题来解决，其中有两条非常经典的独立性假设：
（1）观测独立性假设：任意时刻的观测只依赖于该时刻的马尔可夫链的状态。即：输出观察值之间严格独立。
（2）齐次马尔可夫假设：每个输出仅仅与上一个输出有关。即：状态的转移过程中当前状态只与前一时刻的状态有关，与其他时刻无关（一阶马尔可夫模型）（相当于1-gram）。

针对假设（2），提出了条件随机场算法，使得每个状态不止与他前面的状态有关，还与他后面的状态有关。】

4.1 CRF的定义

1.先看一张概率图模型架构图

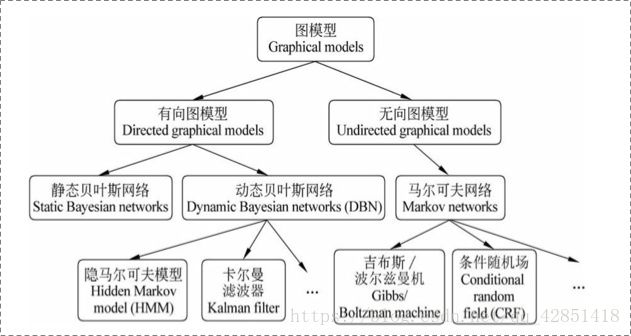
CRF上面是马尔可夫随机场（马尔可夫网络），而CRF是在给定的随机变量$X$（具体，对应观测序列$o_1,\cdot \cdot \cdot ,o_i$）条件下，随机变量$Y$（具体，对应隐状态序列$i_1,\cdot \cdot \cdot ,i_i$）的马尔可夫随机场。

广义的CRF定义如下：

设 $X=(X_1,X_2,X_3,\cdot \cdot \cdot ,X_n)$ 和 $Y=(Y_1,Y_2,Y_3,\dots ,Y_m)$是联合随机变量，若随机变量$Y$构成一个无向图$G=(V,E)$表示的马尔可夫模型，则其条件概率分布$P(Y|X)$称为条件随机场（Conditional Random Field,CRF）,即：
$P(Y_v|X,Y_w,w̸=v)=P(Y_v|X,Y_w,wv)$
对于任何节点v都成立，其中w~v表示图$G=(V,E)$中与结点$v$有边连接的所有节点$w$，$w̸=v$表示除结点$v$以外的所有节点$w$。也就是说，对于点$v$来说，只有与它相连的点会对它产生影响。

简单举例说明随机场概念：现有若干个位置组成的整体，当给定某一个位置按照某种分布随机赋予一个值后，该整体就被称为随机场。

以地名识别为例，假设定义如下规则：

标注	含义
B	当前词为地名命名实体的开始词
M	当前词为地名命名实体的中间词
E	当前词为地名命名实体的结尾词
S	当前词单独构成地名命名实体
O	当前词不是地名命名实体或其组成部分

现有一个由n个字符构成的句子，每个字符的标签都在已知的标签集合中 {“B”，“M”，“E”，“S”，“O”} 选择，当我们为所有字符选定标签后，就形成了一个随机场。
若在其中加一些约束，如所有字符的标签只与相邻的字符标签有关，那么就转化为马尔可夫随机场问题。
假设马尔可夫随机场中有 $X$ 和 $Y$ 两种变量，$X$ 一般是给定的，$Y$ 是在给定 $X$ 条件下的输出。在该例子中，$X$ 是字符，$Y$ 是标签，$P(Y|X)$ 就是条件随机场。

在 CRF 定义中，并没有要求 $X$ 与 $Y$ 具有相同的结构，但实际在自然语言处理中，大多假设其结构相同（ $X$、 $Y$ 中 $m=n$），即：
$X=(X_1,X_2,X_3,\cdot \cdot \cdot ,X_n)$ ， $Y=(Y_1,Y_2,Y_3,\dots ,Y_n)$

一般将这种结构称为线性链条件随机场。定义如下：

设$X=(X_1,X_2,X_3,\cdot \cdot \cdot ,X_n)$和$Y=(Y_1,Y_2,Y_3,\dots ,Y_n)$均为线性链表示的随机变量序列，若在给定的随机变量序列X的条件下，随机变量Y的条件概率分布P(Y|X)构成条件随机场，且满足马尔可夫性: $P(Y_i|X,Y_1,Y_2,\cdot \cdot \cdot ,Y_n)=P(Y_i|X，Y_i{-}_1,Y_i{+}_1))$
则称P(Y|X)为线性链的条件随机场。
也就是说，线性的模型只考虑两边的节点对它的影响，因为只有两边的节点与它相邻。

4.2 CRF 在命名实体识别中的应用

1. 原理

简单地说，CRF 在 NER 中的应用就是，给定一系列的特征去预测每个词的标签。

以地名识别为例，对句子“我去中山公园”进行标注，正确标注后结果应为：“我/O 去/O 中/B 山/M 公/M 园/E”。
即标注序列为（O,O,B,M,M,E）
采用线性链 CRF 来解决，那么上述标注集是其中一种标注序列，（O,O,B,B,M,E）也是一种标注序列，如此有很多的标注序列，NER任务就是在这些可选的标注序列中，找出最靠谱的作为句子的标注。

判断标注序列是否可靠就是目前需要解决的问题。就上述两种标注而言，显然第二种没有第一种准确，因为将“中”和“山”都作为地名开始字标注为了“B”，显然，一个地名不可能有两个开始字。假如给每一条标注序列打分，分值代表标注序列的可靠程度，那么可以定一个规则，若标注中连续出现两个“B”结构的标注序列，则给它打低分（负分，零分等）。

上面说的连续“B”结构打低分就对应一条特征函数。

在CRF中，定义一个特征函数集合，根据该特征集合为标注序列进行打分，根此选出最可靠的标注序列。序列的分值是通过综合考虑特征集合中的函数得出的。

2. 参数化形式

在CRF中，有两种特征函数，分别为转移函数 $t_k(y_i{-}_1,y_i,i)$ 和状态函数 $s_l(y_i,X,i)$。（例如：两个相连的动词可以给负分——转移特征函数；把某个词标注为形容词adj可以给正分——状态特征函数）
$t_k(y_i{-}_1,y_i,i)$ 依赖于当前和前一个位置，表示从标注序列中位置 $i-1$ 的标记 $y_i{-}_1$ 转移到位置 $i$ 上的标记$y_i$ 的概率；
$s_l(y_i,X,i)$ 依赖当前位置，表示标记序列在位置 $i$ 上为标记 $y_i$ 的概率。

通常，特征函数取值为 0 或 1，表示符不符合该条规则约束。

完整的线性链 CRF 的参数形式如下：

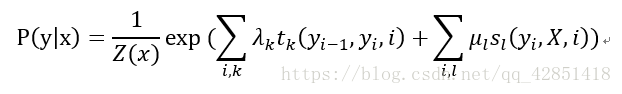
其中

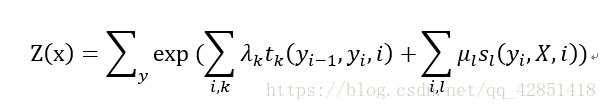
$Z(x)$ 是规范因子，其求和操作是在所有可能的输出序列上做的，其中，归一化是为了让结果算作概率。${\lambda }_k$，${\mu }_l$ 为转移函数和状态函数对应的权值。

为方便计算，上式简化为：

对应的 $Z(x)$ 表示为：

其中，$f_j(y_i{-}_1,y_i,x,i)$ 为

式中 $t_k(y_i{-}_1,y_i,i)$ 和 $s_l(y_i,X,i)$ 的统一符号表示。

使用 CRF 来进行命名实体识别时，目标是求$argma{x}_{y}P(y|x)$。该问题的求解与 HMM 求解最大可能序列路径一样，也是采用 Veterbi 算法。

3.总结

为了建一个条件随机场，首先要定义一个特征函数集，每个特征函数都以整个句子 s，当前位置 i，位置 i 和 i-1 的标签为输入。然后为每一个特征函数赋予一个权重，然后针对每一个标注序列 l，对所有的特征函数加权求和，必要的话，可以把求和的值转化为一个概率值（即归一化）。

在中文信息处理中，分词、词性标注和命名实体识别的方法基本上是互通的，并不限于在某一个具体问题上。当将分词、词性标注和命名实体识别都作为标注任务来进行处理时，采用 HMM 和 CRF 都是可行的，不同的是标签的区别。

参考：
1.解释CRF模型
2.CRF概念与定义

【补充】CRF中的重点概念：判别式模型

1 该类模型工作过程：直接将数据的$Y$（或者label），根据所提供的特征，学习，最后画出了一个明显或者比较明显的边界（具体的，一般通过复杂的函数映射等方法）。如：线性 SVM

2 判别式模型是直接对$P(Y|X)$建模，即，直接根据$X$特征来对$Y$建模训练。

3 关于判别式模型的特征总结如下：
（1）对$P(Y|X)$建模
（2）对所有的样本只构建一个模型，确认总体判别边界
（3）观测到输入什么特征，就预测最可能的 label
（4）另外，判别式优点是：对数据量要求没生成式严格，速度也会快，小数据量下准确率也会好些。

4 关于无向图的联合概率
（1） 概率无向图模型 ——如果联合概率P(Y)满足成对、局部或者全局马尔科夫性，就称该联合概率分布为无向图模型，或者马尔科夫随机场。最大特点：易于因子分解。
（2）团与最大团 ——无向图G中任何两个节点都有边连接的节点子集称为团（clique）。若不能再加进一个节点使团更大，称该团为最大团。

若图太大，可以用因子分解将 $P(Y)$ 写出若干个联合概率的乘积，将一个图分解为若干个“小团”，每个团必须是最大团，则有：

其中，$Z$是归一化因子：

所以对于上面的图有：

其中，${\Psi }_c(Y_c)$是一个最大团C上随机变量们的联合概率，称为势函数，通常定义为指数函数的：

最终得到概率无向图的联合概率分布可以在因子分解下表示为：

而在线性链CRF中，每一个（$I_i,O_i$）对为一个最大团，即上式中$c=i$，并且线性链CRF满足$P(I_i|O,I_1,\cdot \cdot \cdot ,I_n)=P(I_i|O,\cdot \cdot \cdot ,I_i{-}_1;I_i{+}_1)$
所以，CRF 的建模公式为：

_下标$i$表示当前所在的节点（token）的位置。
_下标$k$表示这是第几个特征函数，并且每个特征函数都赋予一个权重值${\lambda }_k$。
_$Z(O)$是用来归一化的，形成概率值。
_$P(I|O)$表示在给定一条观测序列$O=(o_1,\cdot \cdot \cdot ,o_i)$条件下，用CRF所求出来的隐状态序列$I=(i_1,\cdot \cdot \cdot ,i_i)$的概率，