Python-关联分析-从原理到实战
【导读】：本篇文章旨在帮助大家熟悉关联规则算法，并用Python建立模型进行分析。
关联规则中不得不提的故事
在美国，一些年轻的父亲下班后经常要到超市去买婴儿尿布，超市也因此发现了一个规律，在购买婴儿尿布的年轻父亲们中，有30%～40%的人同时要买一些啤酒。超市随后调整了货架的摆放，把尿布和啤酒放在一起，明显增加了销售额。
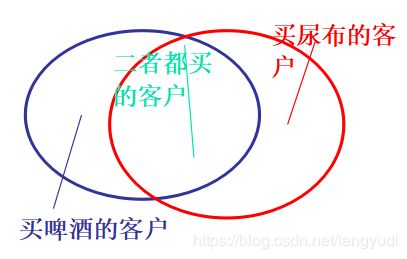
其中若两个或多个变量的取值之间存在某种规律性，就称为关联。关联规则是寻找在同一个事件中出现的不同项的相关性，比如在一次购买活动中所买不同商品的相关性。例如：“在购买计算机的顾客中，有30％的人也同时购买了打印机”
故事讲完了，来看一看你得知道的基本概念
- 一个样本称为一个“事务”
- 每个事务由多个属性来确定，这里的属性称为“项”
- 多个项组成的集合称为“项集”
由k个项构成的集合
- {牛奶}、{啤酒}都是1-项集；
- {牛奶，果冻}是2-项集；
- {啤酒，面包，牛奶}是3-项集
X==>Y含义：
- X和Y是项集
- X称为规则前项（antecedent）
- Y称为规则后项（consequent）
事务仅包含其涉及到的项目，而不包含项目的具体信息。
- 在超级市场的关联规则挖掘问题中事务是顾客一次购物所购买的商品，但事务中并不包含这些商品的具体信息，如商品的数量、价格等。
支持度（support）：一个项集或者规则在所有事务中出现的频率，σ(X):表示项集X的支持度计数
- 项集X的支持度：s(X)=σ(X)/N
- 规则X==>Y表示物品集X对物品集Y的支持度，也就是物品集X和物品集Y同时出现的概率
- 某天共有100个顾客到商场购买物品，其中有30个顾客同时购买了啤酒和尿布，那么上述的关联规则的支持度就是30％
置信度（confidence）：确定Y在包含X的事务中出现的频繁程度。c(X → Y) = σ(X∪Y)/σ(X)
- p（Y│X）＝p（XY）/p(X)。
- 置信度反应了关联规则的可信度—购买了项目集X中的商品的顾客同时也购买了Y中商品的可能性有多大
- 购买薯片的顾客中有50％的人购买了可乐,则置信度为50％
(X , Y)==>Z :
-
支持度:交易中包含{X 、 Y 、 Z}的可能性
-
置信度:包含{X 、 Y}的交易中也包含Z的条件概率
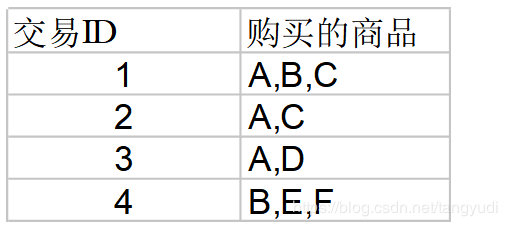
设最小支持度为50%, 最小可信度为 50%, 则可得到 :
- A==>C (50%, 66.6%)
- C==>A (50%, 100%)
若关联规则X->Y的支持度和置信度分别大于或等于用户指定的最小支持率minsupport和最小置信度minconfidence，则称关联规则X->Y为强关联规则，否则称关联规则X->Y为弱关联规则。
提升度（lift）：物品集A的出现对物品集B的出现概率发生了多大的变化
- lift（A==>B）=confidence（A==>B）/support(B)=p(B|A)/p(B)
- 现在有** 1000 ** 个消费者，有** 500** 人购买了茶叶，其中有** 450人同时** 购买了咖啡，另** 50人** 没有。由于** confidence(茶叶=>咖啡)=450/500=90%** ，由此可能会认为喜欢喝茶的人往往喜欢喝咖啡。但如果另外没有购买茶叶的** 500人** ，其中同样有** 450人** 购买了咖啡，同样是很高的** 置信度90%** ,由此，得到不爱喝茶的也爱喝咖啡。这样看来，其实是否购买咖啡，与有没有购买茶叶并没有关联，两者是相互独立的，其** 提升度90%/[(450+450)/1000]=1** 。
由此可见，lift正是弥补了confidence的这一缺陷，if lift=1,X与Y独立，X对Y出现的可能性没有提升作用，其值越大(lift>1),则表明X对Y的提升程度越大，也表明关联性越强。
Leverage 与 Conviction的作用和lift类似，都是值越大代表越关联
- Leverage : P(A,B)-P(A)P(B)
- Conviction:P(A)P(!B)/P(A,!B)
概念搞定之后，来看一看怎么用Python玩玩关联规则
使用mlxtend工具包得出频繁项集与规则
- pip install mlxtend
import pandas as pd
from mlxtend.frequent_patterns import apriori
from mlxtend.frequent_patterns import association_rules
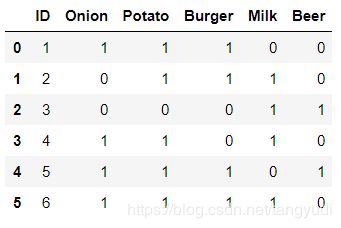
自定义一份购物数据集
data = {'ID':[1,2,3,4,5,6],
'Onion':[1,0,0,1,1,1],
'Potato':[1,1,0,1,1,1],
'Burger':[1,1,0,0,1,1],
'Milk':[0,1,1,1,0,1],
'Beer':[0,0,1,0,1,0]}
df = pd.DataFrame(data)
df = df[['ID', 'Onion', 'Potato', 'Burger', 'Milk', 'Beer' ]]
设置支持度 (support) 来选择频繁项集.
-
选择最小支持度为50%
-
apriori(df, min_support=0.5, use_colnames=True)
frequent_itemsets = apriori(df[['Onion', 'Potato', 'Burger', 'Milk', 'Beer' ]], min_support=0.50, use_colnames=True)
返回的3种项集均是支持度>=50%
计算规则
association_rules(df, metric='lift', min_threshold=1)- 可以指定不同的衡量标准与最小阈值
rules = association_rules(frequent_itemsets, metric='lift', min_threshold=1)
返回的是各个的指标的数值，可以按照感兴趣的指标排序观察,但具体解释还得参考实际数据的含义。
rules [ (rules['lift'] >1.125) & (rules['confidence']> 0.8) ]
这几条结果就比较有价值了：
- （洋葱和马铃薯）（汉堡和马铃薯）可以搭配着来卖
- 如果洋葱和汉堡都在购物篮中, 顾客买马铃薯的可能性也比较高，如果他篮子里面没有，可以推荐一下.
所有指标的计算公式：
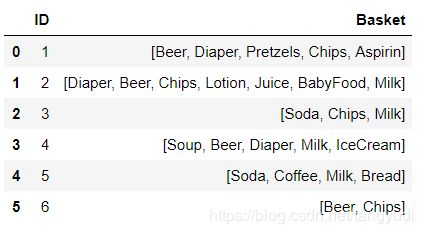
再来加载一份商品数据集
此处需要大家注意如何进行数据预处理，使用工具包一定得按照人家要求来才可以！
retail_shopping_basket = {'ID':[1,2,3,4,5,6],
'Basket':[['Beer', 'Diaper', 'Pretzels', 'Chips', 'Aspirin'],
['Diaper', 'Beer', 'Chips', 'Lotion', 'Juice', 'BabyFood', 'Milk'],
['Soda', 'Chips', 'Milk'],
['Soup', 'Beer', 'Diaper', 'Milk', 'IceCream'],
['Soda', 'Coffee', 'Milk', 'Bread'],
['Beer', 'Chips']
]
}
retail = pd.DataFrame(retail_shopping_basket)
retail = retail[['ID', 'Basket']]
pd.options.display.max_colwidth=100
数据集中都是字符串组成的，需要转换成数值编码
retail_id = retail.drop('Basket' ,1)
retail_Basket = retail.Basket.str.join(',')
retail_Basket = retail_Basket.str.get_dummies(',')
retail = retail_id.join(retail_Basket)
frequent_itemsets_2 = apriori(retail.drop('ID',1), use_colnames=True)
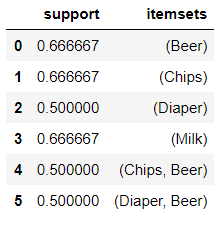
如果光考虑支持度support(X>Y), [Beer, Chips] 和 [Beer, Diaper] 都是很频繁的，哪一种组合更相关呢？
association_rules(frequent_itemsets_2, metric='lift')
显然{Diaper, Beer}更相关一些
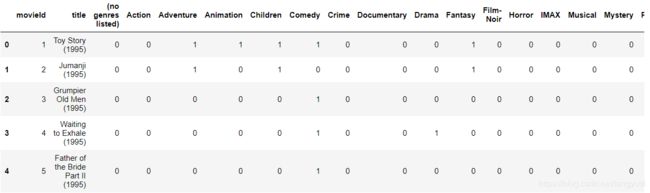
电影数据集关联分析
movies = pd.read_csv('ml-latest-small/movies.csv')
movies.head(10)
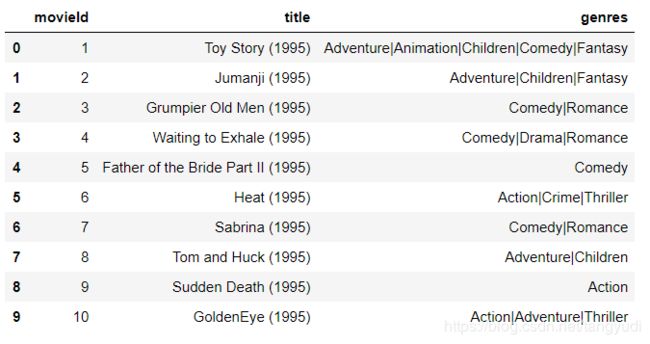
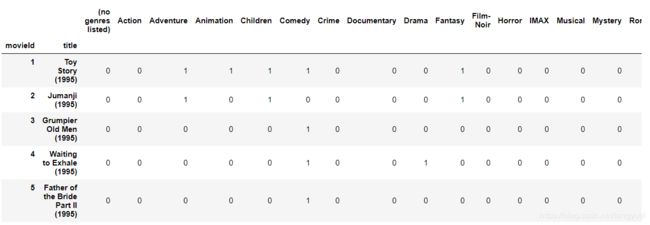
数据中包括电影名字与电影类型的标签，第一步还是先转换成one-hot格式
movies_ohe = movies.drop('genres',1).join(movies.genres.str.get_dummies())
pd.options.display.max_columns=100
movies_ohe.head()
movies_ohe.shape
(9125, 22)
数据集包括9125部电影，一共有22种不同类型
movies_ohe.set_index(['movieId','title'],inplace=True)
movies_ohe.head()
frequent_itemsets_movies = apriori(movies_ohe,use_colnames=True, min_support=0.025)
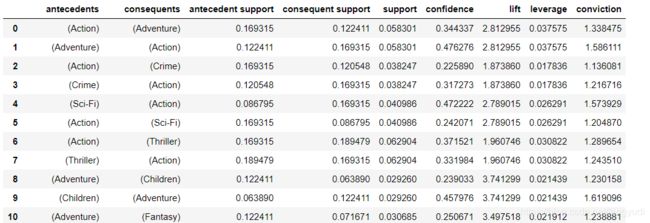
rules_movies = association_rules(frequent_itemsets_movies, metric='lift', min_threshold=1.25)
rules_movies[(rules_movies.lift>4)].sort_values(by=['lift'], ascending=False)
Children和Animation 这俩题材是最相关的了，常识也可以分辨出来。