Python3:《机器学习实战》之AdaBoost算法(2)算法实现
Python3:《机器学习实战》之AdaBoost算法(2)算法实现
- 转载请注明作者和出处:http://blog.csdn.net/u011475210
- 代码地址:https://github.com/WordZzzz/ML/tree/master/Ch07
- 操作系统:WINDOWS 10
- 软件版本:python-3.6.2-amd64
- 编 者:WordZzzz
- Python3机器学习实战之AdaBoost算法2算法实现
- 基于单层决策树构建弱分类器
- 完整AdaBoost算法的实现
- 基于AdaBoost的分类
- 在一个难数据集上应用AdaBoost
基于单层决策树构建弱分类器
单层决策树(decision stump,也称决策树桩)是一种简单的决策树。前面我们已经介绍了决策树的工作原理,接下来将构建一个单层决策树,而它仅基于单个特征来做决策。
首先,需要通过一个简单数据集来确保在算法实现上一切就绪。建立adaboost.py文件并加入如下代码:
#!/usr/bin/env python
# -*- coding: utf-8 -*-
# @Date : 2017-10-10 16:04:14
# @Author : WordZzzz ([email protected])
# @Link : http://blog.csdn.net/u011475210
# @Version : $Id$
from numpy import *
def loadSimpData():
"""
Function: 创建数据集
Input: NULL
Output: datMat:数据集
classLabels:类别标签
"""
#创建数据集
datMat = matrix([[1. , 2.1],
[2. , 1.1],
[1.3, 1. ],
[1. , 1. ],
[2. , 1. ]])
#创建类别标签
classLabels = [1.0, 1.0, -1.0, -1.0, 1.0]
#返回数据集和标签
return datMat, classLabels查看建立的数据集:
>>> import adaboost
>>> datMat, classLabels = adaboost.loadSimpData()
>>> datMat
matrix([[ 1. , 2.1],
[ 2. , 1.1],
[ 1.3, 1. ],
[ 1. , 1. ],
[ 2. , 1. ]])
>>> classLabels
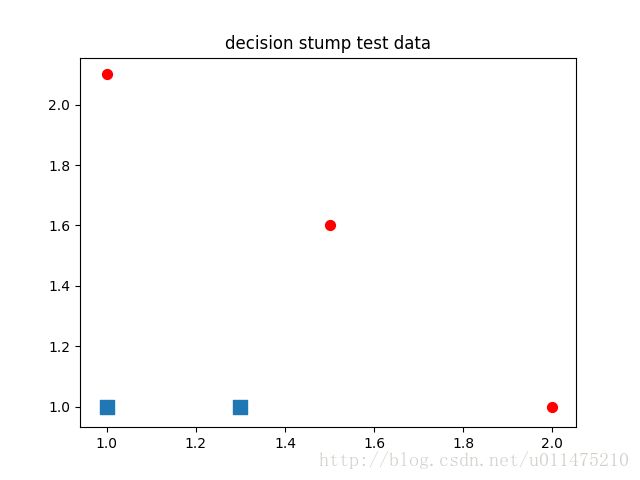
[1.0, 1.0, -1.0, -1.0, 1.0]可视化结果:
接下来,构建单层决策树,伪代码如下:
将最小错误率minEroor设为无穷大
对数据集中的每一个特征(第一层循环):
对每个步长(第二层循环):
对每个不等号(第三层循环):
建立一颗单层决策树并利用加权数据集对它进行测试
如果错误率低于minError,则将当前单层决策树设为最佳单层决策树
返回最佳单层决策树单层决策树生成函数代码如下:
def stumpClassify(dataMatrix, dimen, threshVal, threshIneq):
"""
Function: 通过阈值比较对数据进行分类
Input: dataMatrix:数据集
dimen:数据集列数
threshVal:阈值
threshIneq:比较方式:lt,gt
Output: retArray:分类结果
"""
#新建一个数组用于存放分类结果,初始化都为1
retArray = ones((shape(dataMatrix)[0],1))
#lt:小于,gt;大于;根据阈值进行分类,并将分类结果存储到retArray
if threshIneq == 'lt':
retArray[dataMatrix[:, dimen] <= threshVal] = -1.0
else:
retArray[dataMatrix[:, dimen] > threshVal] = -1.0
#返回分类结果
return retArray
def buildStump(dataArr, classLabels, D):
"""
Function: 找到最低错误率的单层决策树
Input: dataArr:数据集
classLabels:数据标签
D:权重向量
Output: bestStump:分类结果
minError:最小错误率
bestClasEst:最佳单层决策树
"""
#初始化数据集和数据标签
dataMatrix = mat(dataArr); labelMat = mat(classLabels).T
#获取行列值
m,n = shape(dataMatrix)
#初始化步数,用于在特征的所有可能值上进行遍历
numSteps = 10.0
#初始化字典,用于存储给定权重向量D时所得到的最佳单层决策树的相关信息
bestStump = {}
#初始化类别估计值
bestClasEst = mat(zeros((m,1)))
#将最小错误率设无穷大,之后用于寻找可能的最小错误率
minError = inf
#遍历数据集中每一个特征
for i in range(n):
#获取数据集的最大最小值
rangeMin = dataMatrix[:,i].min(); rangeMax = dataMatrix[:,i].max()
#根据步数求得步长
stepSize = (rangeMax - rangeMin) / numSteps
#遍历每个步长
for j in range(-1, int(numSteps) + 1):
#遍历每个不等号
for inequal in ['lt', 'gt']:
#设定阈值
threshVal = (rangeMin + float(j) * stepSize)
#通过阈值比较对数据进行分类
predictedVals = stumpClassify(dataMatrix, i, threshVal, inequal)
#初始化错误计数向量
errArr = mat(ones((m,1)))
#如果预测结果和标签相同,则相应位置0
errArr[predictedVals == labelMat] = 0
#计算权值误差,这就是AdaBoost和分类器交互的地方
weightedError = D.T * errArr
#打印输出所有的值
#print("split: dim %d, thresh %.2f, thresh ineqal: %s, the weighted error is %.3f" % (i, threshVal, inequal, weightedError))
#如果错误率低于minError,则将当前单层决策树设为最佳单层决策树,更新各项值
if weightedError < minError:
minError = weightedError
bestClasEst = predictedVals.copy()
bestStump['dim'] = i
bestStump['thresh'] = threshVal
bestStump['ineq'] = inequal
#返回最佳单层决策树,最小错误率,类别估计值
return bestStump, minError, bestClasEst测试:
>>> from numpy import *
>>> D = mat(ones((5,1))/5)
>>> adaboost.buildStump(datMat, classLabels, D)
({'dim': 0, 'thresh': 1.3, 'ineq': 'lt'}, matrix([[ 0.2]]), array([[-1.],
[ 1.],
[-1.],
[-1.],
[ 1.]]))上述单层决策树的生成函数是决策树的一个简化版本。它就是所谓的弱学习器,即弱分类算法。其中,weightError是AdaBoost和分类器交互的地方,大家可以留意一下。
完整AdaBoost算法的实现
完成AdaBoost算法的伪代码如下:
对每次迭代:
利用buildStump()函数找到最佳的单层决策树
将最佳单层决策树加入到单层决策树数组
计算alpha
计算新的权重向量D
更新累计类别估计值
如果错误率等于0.0,则退出循环代码实现如下:
def adaBoostTrainDS(dataArr, classLabels, numIt = 40):
"""
Function: 找到最低错误率的单层决策树
Input: dataArr:数据集
classLabels:数据标签
numIt:迭代次数
Output: weakClassArr:单层决策树列表
aggClassEst:类别估计值
"""
#初始化列表,用来存放单层决策树的信息
weakClassArr = []
#获取数据集行数
m = shape(dataArr)[0]
#初始化向量D每个值均为1/m,D包含每个数据点的权重
D = mat(ones((m,1))/m)
#初始化列向量,记录每个数据点的类别估计累计值
aggClassEst = mat(zeros((m,1)))
#开始迭代
for i in range(numIt):
#利用buildStump()函数找到最佳的单层决策树
bestStump, error, classEst = buildStump(dataArr, classLabels, D)
#print("D: ", D.T)
#根据公式计算alpha的值,max(error, 1e-16)用来确保在没有错误时不会发生除零溢出
alpha = float(0.5 * log((1.0 - error) / max(error, 1e-16)))
#保存alpha的值
bestStump['alpha'] = alpha
#填入数据到列表
weakClassArr.append(bestStump)
#print("classEst: ", classEst.T)
#为下一次迭代计算D
expon = multiply(-1 * alpha * mat(classLabels).T, classEst)
D = multiply(D, exp(expon))
D = D / D.sum()
#累加类别估计值
aggClassEst += alpha * classEst
#print("aggClassEst: ", aggClassEst.T)
#计算错误率,aggClassEst本身是浮点数,需要通过sign来得到二分类结果
aggErrors = multiply(sign(aggClassEst) != mat(classLabels).T, ones((m,1)))
errorRate = aggErrors.sum() / m
print("total error: ", errorRate)
#如果总错误率为0则跳出循环
if errorRate == 0.0: break
#返回单层决策树列表和累计错误率
return weakClassArr
#return weakClassArr, aggClassEst测试如下:
>>> from imp import reload
>>> reload(adaboost)
'adaboost' from 'E:\\机器学习实战\\mycode\\Ch07\\adaboost.py'>
>>> classifierArr = adaboost.adaBoostTrainDS(datMat, classLabels, 9)
D: [[ 0.2 0.2 0.2 0.2 0.2]]
classEst: [[-1. 1. -1. -1. 1.]]
aggClassEst: [[-0.69314718 0.69314718 -0.69314718 -0.69314718 0.69314718]]
total error: 0.2
D: [[ 0.5 0.125 0.125 0.125 0.125]]
classEst: [[ 1. 1. -1. -1. -1.]]
aggClassEst: [[ 0.27980789 1.66610226 -1.66610226 -1.66610226 -0.27980789]]
total error: 0.2
D: [[ 0.28571429 0.07142857 0.07142857 0.07142857 0.5 ]]
classEst: [[ 1. 1. 1. 1. 1.]]
aggClassEst: [[ 1.17568763 2.56198199 -0.77022252 -0.77022252 0.61607184]]
total error: 0.0
>>> classifierArr
[{'dim': 0, 'thresh': 1.3, 'ineq': 'lt', 'alpha': 0.6931471805599453}, {'dim': 1, 'thresh': 1.0, 'ineq': 'lt', 'alpha': 0.9729550745276565}, {'dim': 0, 'thresh': 0.90000000000000002, 'ineq': 'lt', 'alpha': 0.8958797346140273}] 我们观察中间的运行结果,可以发现,第一轮迭代中,D中的所有值都相等,于是,只有第一个数据点被错分了。第二轮迭代中,D向量给第一个数据点0.5的权重。这就可以通过变量aggClassEst的符号来了解总的类别。第二次迭代之后,我们就会发现第一个数据点已经正确分类了,但最后一个数据点错分了。D向量中的最后一个元素变成0.5,而D向量中的其他值都变得非常小。最后,第三次迭代后aggClassEst所有值的符号和真实类别标签都完全吻合,那么训练错误率为0,程序就此退出。
基于AdaBoost的分类
一旦拥有了多个弱分类器以及其对应的alpha值,进行测试就变得相当容易了。现在,我们就将之前的代码应用到具体的实例上去。每个分类器的结果以其对应的alpha值作为权重。所有这些弱分类器的结果加权求和就得到了最后的结果。
代码实现:
def adaClassify(datToClass, classifierArr):
"""
Function: AdaBoost分类函数
Input: datToClass:待分类样例
classifierArr:多个弱分类器组成的数组
Output: sign(aggClassEst):分类结果
"""
#初始化数据集
dataMatrix = mat(datToClass)
#获得待分类样例个数
m = shape(dataMatrix)[0]
#构建一个初始化为0的列向量,记录每个数据点的类别估计累计值
aggClassEst = mat(zeros((m,1)))
#遍历每个弱分类器
for i in range(len(classifierArr)):
#基于stumpClassify得到类别估计值
classEst = stumpClassify(dataMatrix, classifierArr[i]['dim'], classifierArr[i]['thresh'], classifierArr[i]['ineq'])
#累加类别估计值
aggClassEst += classifierArr[i]['alpha']*classEst
#打印aggClassEst,以便我们了解其变化情况
#print(aggClassEst)
#返回分类结果,aggClassEst大于0则返回+1,否则返回-1
return sign(aggClassEst)测试结果:
>>> from imp import reload
>>> reload(adaboost)
'adaboost' from 'E:\\机器学习实战\\mycode\\Ch07\\adaboost.py'>
>>> datMat, classLabels = adaboost.loadSimpData()
>>> classifierArr = adaboost.adaBoostTrainDS(datMat, classLabels, 30)
D: [[ 0.2 0.2 0.2 0.2 0.2]]
classEst: [[-1. 1. -1. -1. 1.]]
aggClassEst: [[-0.69314718 0.69314718 -0.69314718 -0.69314718 0.69314718]]
total error: 0.2
D: [[ 0.5 0.125 0.125 0.125 0.125]]
classEst: [[ 1. 1. -1. -1. -1.]]
aggClassEst: [[ 0.27980789 1.66610226 -1.66610226 -1.66610226 -0.27980789]]
total error: 0.2
D: [[ 0.28571429 0.07142857 0.07142857 0.07142857 0.5 ]]
classEst: [[ 1. 1. 1. 1. 1.]]
aggClassEst: [[ 1.17568763 2.56198199 -0.77022252 -0.77022252 0.61607184]]
total error: 0.0
>>> classifierArr
[{'dim': 0, 'thresh': 1.3, 'ineq': 'lt', 'alpha': 0.6931471805599453}, {'dim': 1, 'thresh': 1.0, 'ineq': 'lt', 'alpha': 0.9729550745276565}, {'dim': 0, 'thresh': 0.90000000000000002, 'ineq': 'lt', 'alpha': 0.8958797346140273}]
>>> adaboost.adaClassify([0,0], classifierArr)
[[-0.69314718]]
[[-1.66610226]]
[[-2.56198199]]
matrix([[-1.]])
>>> adaboost.adaClassify([[5,5],[0,0]], classifierArr)
[[ 0.69314718]
[-0.69314718]]
[[ 1.66610226]
[-1.66610226]]
[[ 2.56198199]
[-2.56198199]]
matrix([[ 1.],
[-1.]]) 我们可以看到,随着迭代的进行,分类结果越来越强。下面我们换个数据集。
在一个难数据集上应用AdaBoost
这次我们在之前给出的马疝病数据集上应用AdaBoost分类器,之前用的是Logistic回归。
示例:在一个难数据集上的AdaBoost应用
- 收集数据:提供的文本文件。
- 准备数据:确保类别标签是+1和-1而非1和0。
- 分析数据:手工检查数据。
- 训练算法:在数据上,利用adaBoostTrainDS()函数训练出一系列的分类器。
- 测试算法:我们拥有两个数据集。在不采用随机抽样的方法下,我们就会对AdaBoost和Logistic回归的结果进行完全对等的比较。
- 使用算法:观察该例子上的错误率。不过,这可以构建一个web网站,让驯马师输入马的症状然后预测马是否会死去。
加入我们最熟悉的代码,唯一的区别就是这次是自动识别特征数目的。
def loadDataSet(fileName):
"""
Function: 自适应数据加载函数
Input: fileName:文件名称
Output: dataMat:数据集
labelMat:类别标签
"""
#自动获取特征个数,这是和之前不一样的地方
numFeat = len(open(fileName).readline().split('\t'))
#初始化数据集和标签列表
dataMat = []; labelMat = []
#打开文件
fr = open(fileName)
#遍历每一行
for line in fr.readlines():
#初始化列表,用来存储每一行的数据
lineArr = []
#切分文本
curLine = line.strip().split('\t')
#遍历每一个特征,某人最后一列为标签
for i in range(numFeat-1):
#将切分的文本全部加入行列表中
lineArr.append(float(curLine[i]))
#将每个行列表加入到数据集中
dataMat.append(lineArr)
#将每个标签加入标签列表中
labelMat.append(float(curLine[-1]))
#返回数据集和标签列表
return dataMat, labelMat分类结果:
>>> from imp import reload
>>> reload(adaboost)
'adaboost' from 'E:\\机器学习实战\\mycode\\Ch07\\adaboost.py'>
>>> datArr, labelArr = adaboost.loadDataSet('horseColicTraining2.txt')
>>> classifierArr = adaboost.adaBoostTrainDS(datArr, labelArr, 10)
total error: 0.284280936455
total error: 0.284280936455
total error: 0.247491638796
total error: 0.247491638796
total error: 0.254180602007
total error: 0.240802675585
total error: 0.240802675585
total error: 0.220735785953
total error: 0.247491638796
total error: 0.230769230769
>>> testArr, testLabelArr = adaboost.loadDataSet('horseColicTest2.txt')
>>> prediction10 = adaboost.adaClassify(testArr, classifierArr)
>>> errArr = mat(ones((67,1)))
Traceback (most recent call last):
File "" , line 1, in
NameError: name 'mat' is not defined
>>> from numpy import *
>>> errArr = mat(ones((67,1)))
>>> errArr[prediction10 != mat(testLabelArr).T].sum()
16.0 书上给了个表,我们直接来看表格数据:
| Number of Classifiers | Training Error | Test Error |
|---|---|---|
| 1 | 0.28 | 0.27 |
| 10 | 0.23 | 0.24 |
| 50 | 0.19 | 0.21 |
| 100 | 0.19 | 0.22 |
| 500 | 0.16 | 0.25 |
| 1000 | 0.14 | 0.31 |
| 10000 | 0.11 | 0.33 |
我们发现,测试错误率在到达一个最小值之后又开始上升了。这类现象就是过拟合(overfitting)。有文献称,对于表现好的数据集,AdaBoost的测试错误率就会达到一个稳定值,并不会随着分类器的增多而上升。但是别忘了,我们这个数据集可是有百分之三十的缺失值哦。
很多人认为,AdaBoost和SVM是监督机器学习中最强大的两种方法。实际上,这两者之间拥有不少相似之处。我们可以把弱分类器想象成SVM中的一个核函数,也可以按照最大化某个最小间隔的方式重写AdaBoost算法。而他们的不同之处在于所定义的间隔计算方式有所不同。因此导致的结果也不同。特别是在高位空间下,这两者之间的差异就会更加明显。
至此,分类算法部分全部介绍完了,之后的回归、无监督学习等等,有机会了再更吧。
系列教程持续发布中,欢迎订阅、关注、收藏、评论、点赞哦~~( ̄▽ ̄~)~
完的汪(∪。∪)。。。zzz