通信里 星座图 到底是什么
本文根据知乎的一篇文章整理而来。
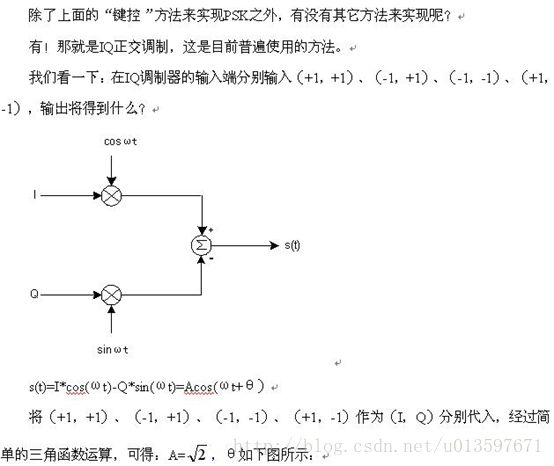
要说星座图，要先从IQ调制说起：
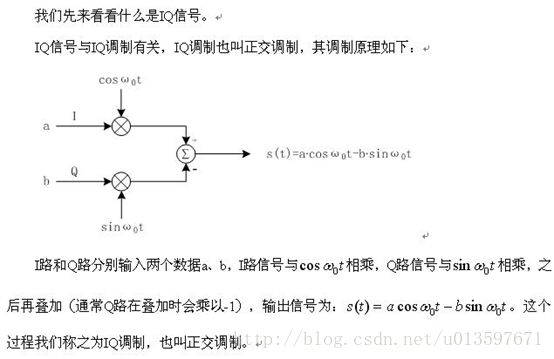
##IQ调制：
##IQ解调原理：
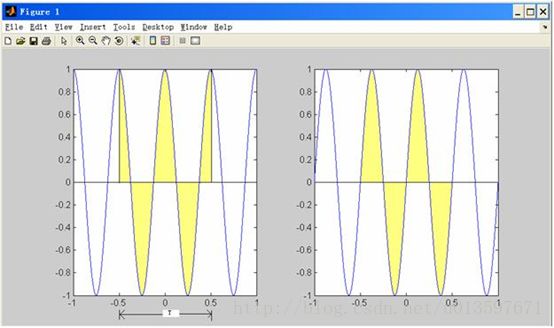
t=-1:0.001:1;
f=1;
y=cos(2*pi*2*f*t);
subplot(1,2,1);plot(t,y);
y=sin(2*pi*2*f*t);
subplot(1,2,2);plot(t,y);
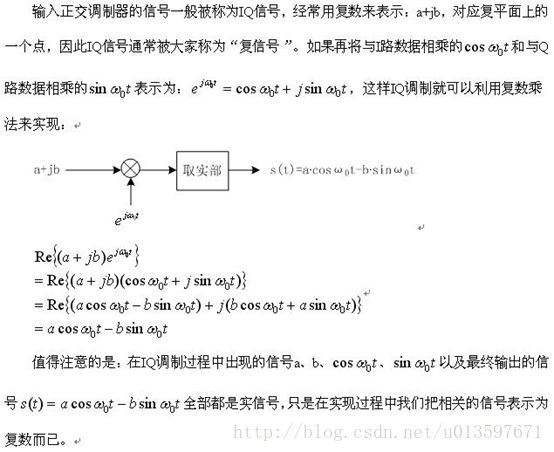
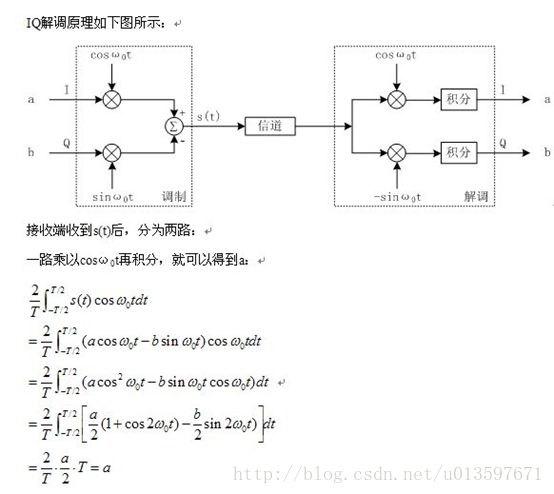
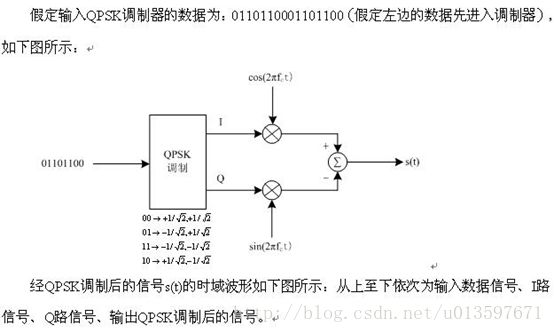
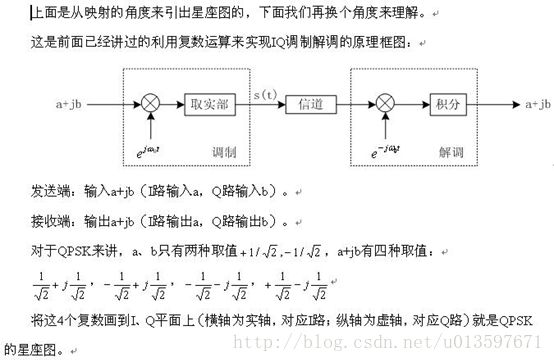
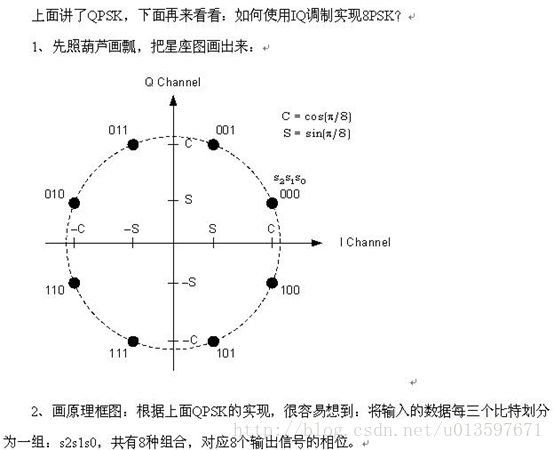
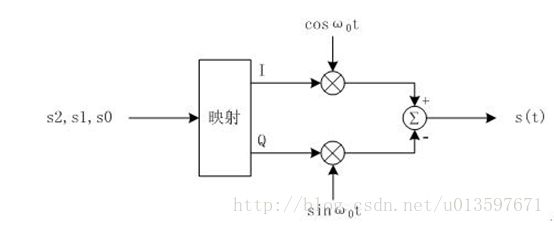
前面我们讲了IQ调制和解调的原理，下来我们看一下如何应用IQ调制来实现MPSK调制（QPSK、8PSK等）、MQAM调制（16QAM、64QAM等）。
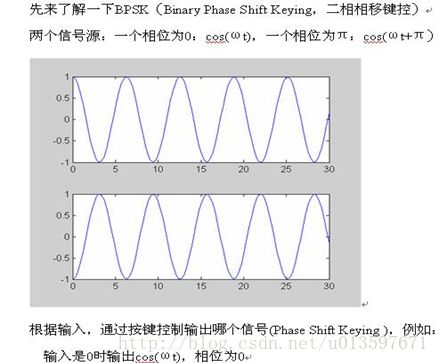
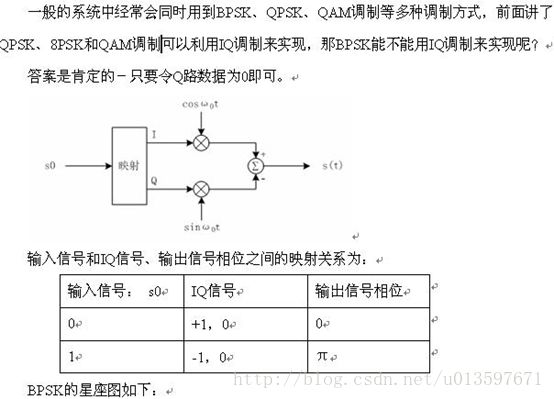
##BPSK 二相相移键控
先来了解一下BPSK（Binary Phase Shift Keying，二相相移键控）
##如何用IQ调制实现QPSK调制？
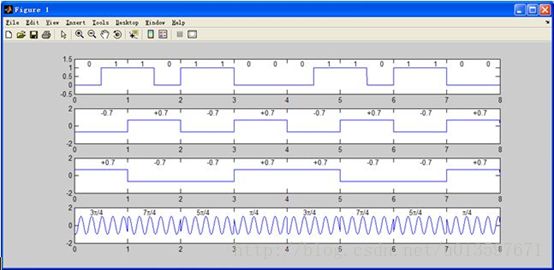
%输入信号
>>subplot(4,1,1);
>> t=0:0.001:8;
>> d=[0 0 ;0.5 1;1 1;1.5 0;2 1;2.5 1;3 0;3.5 0;4 0;4.5 1 ;5 1 ;5.5 0 ;6 1 ;6.5 1 ;7 0 ;7.5 0];
>> s=pulstran(t-0.25,d,'rectpuls',0.5);plot(t,s) ;
>> axis([0 8 -0.5 1.5]);
>> text(0.25,1.2,'0') ;text(0.75,1.2,'1') ; text(1.25,1.2,'1') ; text(1.75,1.2,'0') ;
>> text(2.25,1.2,'1'); text(2.75,1.2,'1') ; text(3.25,1.2,'0') ; text(3.75,1.2,'0') ;
>> text(4.25,1.2,'0'); text(4.75,1.2,'1') ; text(5.25,1.2,'1') ; text(5.75,1.2,'0') ;
>> text(6.25,1.2,'1'); text(6.75,1.2,'1') ; text(7.25,1.2,'0') ; text(7.75,1.2,'0') ;
% I路信号
>> subplot(4,1,2);
>> t=0:0.001:8;
>> a=1/sqrt(2);
>> d=[0 -a ;1 +a;2 -a;3 +a; 4 -a;5 +a;6 -a;7 +a];
>> s=pulstran(t-0.5,d,'rectpuls');plot(t,s) ;
>> axis([0 8 -2 2]);
>> text(0.5,1.5,'-0.7') ; text(1.5,1.5,'+0.7') ;text(2.5,1.5,'-0.7') ;text(3.5,1.5,'+0.7');
>> text(4.5,1.5,'-0.7') ; text(5.5,1.5,'+0.7') ;text(6.5,1.5,'-0.7') ;text(7.5,1.5,'+0.7');
% Q路信号
>> subplot(4,1,3);
>> t=0:0.001:8;
>> d=[0 +a;1 -a;2 -a;3 +a; 4 +a;5 -a;6 -a;7 +a];
>> s=pulstran(t-0.5,d,'rectpuls');plot(t,s) ;
>> axis([0 8 -2 2]);
>> text(0.5,1.5,'+0.7'); text(1.5,1.5,'-0.7') ; text(2.5,1.5,'-0.7') ; text(3.5,1.5,'+0.7')
>> text(4.5,1.5,'+0.7'); text(5.5,1.5,'-0.7') ; text(6.5,1.5,'-0.7') ; text(7.5,1.5,'+0.7')
%QPSK调制信号
>> subplot(4,1,4);
>> t=0:0.001:8;
>> d1=[0 -a ;1 +a;2 -a;3 +a; 4 -a ;5 +a;6 -a;7 +a];
>> s1=pulstran(t-0.5,d1,'rectpuls').*cos(2*pi*5*t);
>> d2=[0 +a;1 -a;2 -a;3 +a; 4 +a;5 -a;6 -a;7 +a];
>> s2=pulstran(t-0.5,d2,'rectpuls').*sin(2*pi*5*t);
>> plot(t,s1-s2) ;>> axis([0 8 -2 2]);
>> text(0.3,1.5,'3\pi/4') ; text(1.3,1.5, '7\pi/4') ; text(2.3,1.5,'5\pi/4') ; text(3.3,1.5,'\pi/4') ;
>> text(4.3,1.5, '3\pi/4') ; text(5.3,1.5, '7\pi/4');
text(6.3,1.5,'5\pi/4') ; text(7.3,1.5,'\pi/4') ;
##QPSK调制的星座图
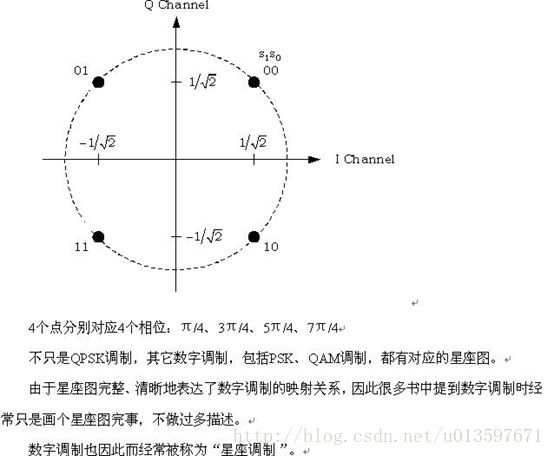
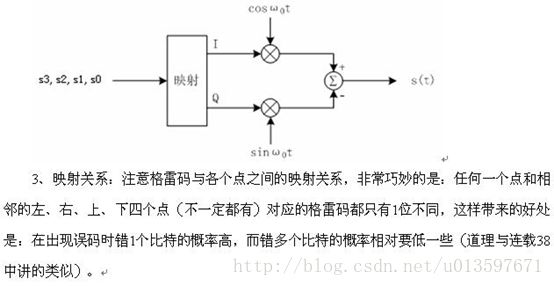
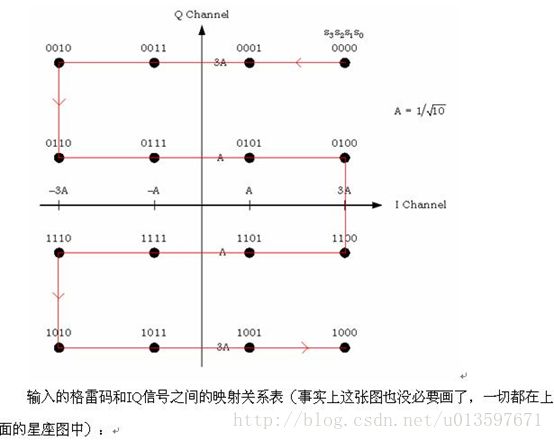
星座图，就是说一个坐标，如高中的单位圆，横坐标是I，纵坐标是Q，相应于投影到I轴的，叫同相分量，同理投影到Q轴的叫正交分量。由于信号幅度有差别，那么就有可能落在单位圆之内。具体地说，64QAM，符号有64个，等于2的6次方，因此每个符号需要6个二进制来代表才够用。这64个符号就落在单位圆内，根据幅度和相位的不同 落的地方也不同。从其中一个点跳到另一个点，就意味着相位调制和幅度调制同时完成了。”
##QPSK的映射关系可以随意定吗？
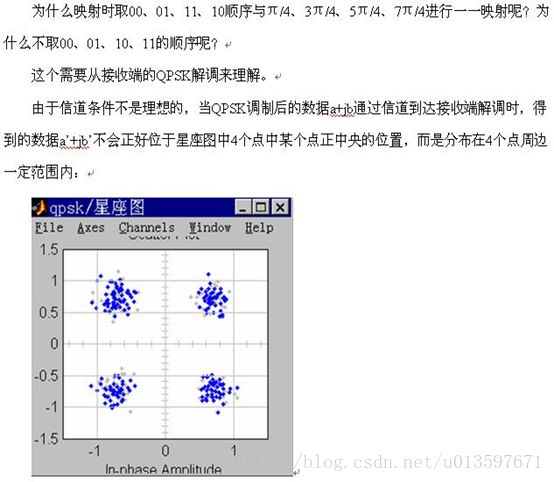
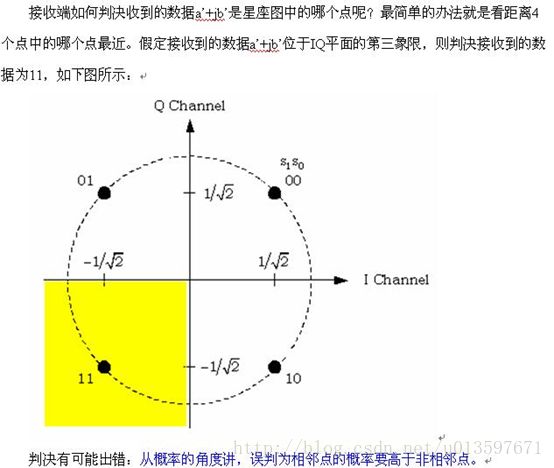
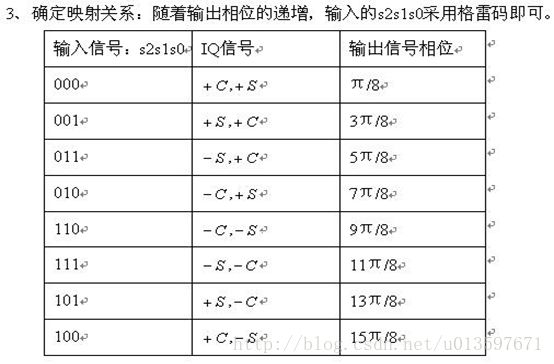
还以发送数据是11为例，接收数据误判为10和00的概率要高于误判为01的概率。11误判为10错了1个比特，但11误判为00却错了2个比特。 综上所述，在相同的信道条件下，采用00↔π/4、01↔3π/4、10↔5π/4、11↔7π/4映射关系的QPSK调制的误比特率要高于采用00↔π/4、01↔3π/4、11↔5π/4、10↔7π/4映射关系。 象00、01、11、10这样，相邻的两个码之间只有1位数字不同的编码叫做格雷码。QPSK调制中使用的就是格雷码。
| 十进制数 | 自然二进制数 | 格雷码 |
|---|---|---|
| 0 | 0000 | 0000 |
| 1 | 0001 | 0001 |
| 2 | 0010 | 0011 |
| 3 | 0011 | 0010 |
| 4 | 0100 | 0110 |
| 5 | 0101 | 0111 |
| 6 | 0110 | 0101 |
| 7 | 0111 | 0100 |
| 8 | 1000 | 1100 |
| 9 | 1001 | 1101 |
| 10 | 1010 | 1111 |
| 11 | 1011 | 1110 |
| 12 | 1100 | 1010 |
| 13 | 1101 | 1011 |
| 14 | 1110 | 1001 |
| 15 | 1111 | 1000 |
##如何使用IQ调制实现8PSK？
##如何使用IQ调制实现16QAM？
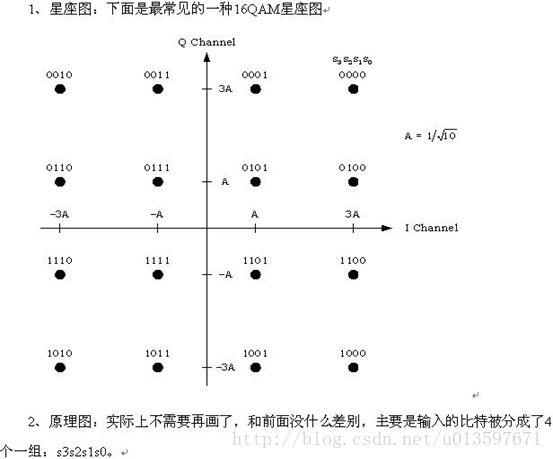
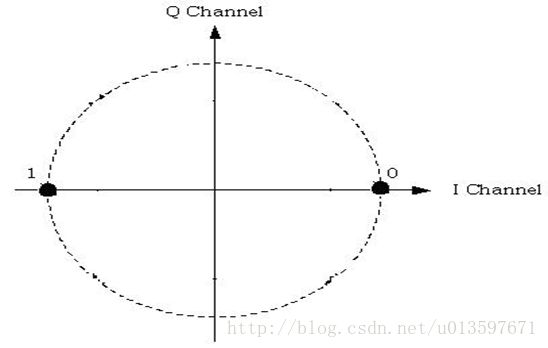
前面讲的PSK调制（QPSK、8PSK），星座图中的点都位于单位圆上，模相同（都为1），只有相位不同。而QAM调制星座图中的点不再位于单位圆上，而是分布在复平面的一定范围内，各点如果模相同，则相位必不相同，如果相位相同则模必不相同。星座图中点的分布是有讲究的，不同的分布和映射关系对应的调制方案的误码性能是不一样的，这里不再展开去讲。
##利用IQ调制实现BPSK调制
