手眼标定(一):Opencv4实现手眼标定及手眼系统测试
Opencv4实现手眼标定及手眼系统测试
- 前言
- 1 程序环境
- 2 原理
- 3 程序源码
- 4 程序输出
- 5 数据分析
- 6 总结
- 7 其他
前言
由于项目需要,要在win10环境下实现“眼在手上”的手眼系统,为此查阅了不少资料。但大多是理论资料,或者不可用的代码。虽然本人基于Halcon 12.0实现了手眼标定,但代码太冗余,效率低。因此本人拟通过Opencv4实现手眼标定。
(第一次写博客,不足之处敬请批评指正!)
1 程序环境
- 编译器:Visual Studio 2015;
- Opencv版本:Opencv3.4.6、或Opencv4以上版本;
2 原理
(1)主要使用Opencv的calibrateHandEye()函数,其中包括五种方法,相关文献见链接link。
(2)本代码主要根据Tsai两步法进行,利用公式AX=XB,先计算旋转矩阵R,再计算平移矩阵T。
(3)Tsai两步法的原理可参考博主一“手眼标定”: link;博主二“机械臂的手眼标定 opencv实现”:link.
3 程序源码
主要参考github代码1: link;github代码2:link.
本人整理优化后的源码如下:
/***********************************************************************
说明:Opencv4实现手眼标定及手眼测试
作者:jian xu @CUG
日期:2020年01月08日
***********************************************************************/
#include <iostream>
#include <string>
#include <opencv2/opencv.hpp>
#include <opencv2/core.hpp>
#include <opencv2/imgproc.hpp>
#include <opencv2/calib3d.hpp>
//导入静态链接库
#if (defined _WIN32 || defined WINCE || defined __CYGWIN__)
#define OPENCV_VERSION "412"
#pragma comment(lib, "opencv_world" OPENCV_VERSION ".lib")
#endif
using namespace cv;
using namespace std;
//相机中13组标定板的位姿,x,y,z,rx,ry,rz,
Mat_<double> CalPose = (cv::Mat_<double>(13, 6) <<
-0.072944147641399, -0.06687830562048944, 0.4340418493881254, -0.2207496117519063, 0.0256862005614321, 0.1926014162476009,
-0.01969337858360518, -0.05095294728651902, 0.3671266719105768, 0.1552099329677287, -0.5763323472739464, 0.09956130526058841,
0.1358164536530692, -0.1110802522656379, 0.4001396735998251, -0.04486168331242635, -0.004268942058870162, 0.05290073845562016,
0.1360676260120161, -0.002373036366121294, 0.3951670952829301, -0.4359637938379769, 0.00807193982932386, 0.06162504121755787,
-0.1047666520352697, -0.01377729010376614, 0.4570029374109721, -0.612072103513551, -0.04939465180949879, -0.1075464055169537,
0.02866460103085085, -0.1043911269729344, 0.3879127305077527, 0.3137563103168434, -0.02113958397023016, 0.1311397970432597,
0.1122741829392126, 0.001044006395747612, 0.3686697279333643, 0.1607160803445018, 0.2468677059920437, 0.1035103912091547,
-0.06079521129779342, -0.02815190820828123, 0.4451740202390909, 0.1280935541917056, -0.2674407142401368, 0.1633865613363686,
-0.02475533256363622, -0.06950841248698086, 0.2939836207787282, 0.1260629671933584, -0.2637748974005461, 0.1634102148863728,
0.1128618887222624, 0.00117877722121125, 0.3362496409334229, 0.1049541359309871, -0.2754352318773509, 0.4251492928748009,
0.1510545750008333, -0.0725019944548204, 0.3369908269102371, 0.2615745097093249, -0.1295598776133405, 0.6974394284203849,
0.04885313290076512, -0.06488755216394324, 0.2441532410787161, 0.1998243391807502, -0.04919417529483511, -0.05133193756053007,
0.08816140480523708, -0.05549965109057759, 0.3164905645998022, 0.164693654482863, 0.1153894876338608, 0.01455551646362294);
//机械臂末端13组位姿,x,y,z,rx,ry,rz
Mat_<double> ToolPose = (cv::Mat_<double>(13, 6) <<
-0.3969707, -0.460018, 0.3899877, 90.2261, -168.2015, 89.7748,
-0.1870185, -0.6207147, 0.2851157, 57.2636, -190.2034, 80.7958,
-0.1569776, -0.510021, 0.3899923, 90.225, -178.2038, 81.7772,
-0.1569787, -0.5100215, 0.3299975, 90.2252, -156.205, 81.7762,
-0.3369613, -0.4100348, 0.3299969, 90.2264, -146.2071, 71.778,
-0.2869552, -0.6100449, 0.4299998, 90.2271, -199.2048, 86.7806,
-0.2869478, -0.6600489, 0.4299948, 105.2274, -189.2053, 86.7814,
-0.286938, -0.6300559, 0.4299997, 75.2279, -189.2056, 86.783,
-0.2869343, -0.5700635, 0.2800084, 75.2291, -189.2055, 86.7835,
-0.1669241, -0.5700796, 0.280015, 75.2292, -189.205, 101.7845,
-0.236909, -0.4700997, 0.3600046, 87.2295, -196.2063, 118.7868,
-0.2369118, -0.6201035, 0.2600001, 87.2297, -192.2087, 75.7896,
-0.2468983, -0.620112, 0.359992, 97.2299, -190.2082, 80.7908);
//R和T转RT矩阵
Mat R_T2RT(Mat &R, Mat &T)
{
Mat RT;
Mat_<double> R1 = (cv::Mat_<double>(4, 3) << R.at<double>(0, 0), R.at<double>(0, 1), R.at<double>(0, 2),
R.at<double>(1, 0), R.at<double>(1, 1), R.at<double>(1, 2),
R.at<double>(2, 0), R.at<double>(2, 1), R.at<double>(2, 2),
0.0, 0.0, 0.0);
cv::Mat_<double> T1 = (cv::Mat_<double>(4, 1) << T.at<double>(0, 0), T.at<double>(1, 0), T.at<double>(2, 0),1.0);
cv::hconcat(R1, T1, RT);//C=A+B左右拼接
return RT;
}
//RT转R和T矩阵
void RT2R_T(Mat &RT, Mat &R, Mat &T)
{
cv::Rect R_rect(0, 0, 3, 3);
cv::Rect T_rect(3, 0, 1, 3);
R = RT(R_rect);
T = RT(T_rect);
}
//判断是否为旋转矩阵
bool isRotationMatrix(const cv::Mat & R)
{
cv::Mat tmp33 = R({ 0,0,3,3 });
cv::Mat shouldBeIdentity;
shouldBeIdentity = tmp33.t()*tmp33;
cv::Mat I = cv::Mat::eye(3, 3, shouldBeIdentity.type());
return cv::norm(I, shouldBeIdentity) < 1e-6;
}
/** @brief 欧拉角 -> 3*3 的R
* @param eulerAngle 角度值
* @param seq 指定欧拉角xyz的排列顺序如:"xyz" "zyx"
*/
cv::Mat eulerAngleToRotatedMatrix(const cv::Mat& eulerAngle, const std::string& seq)
{
CV_Assert(eulerAngle.rows == 1 && eulerAngle.cols == 3);
eulerAngle /= 180 / CV_PI;
cv::Matx13d m(eulerAngle);
auto rx = m(0, 0), ry = m(0, 1), rz = m(0, 2);
auto xs = std::sin(rx), xc = std::cos(rx);
auto ys = std::sin(ry), yc = std::cos(ry);
auto zs = std::sin(rz), zc = std::cos(rz);
cv::Mat rotX = (cv::Mat_<double>(3, 3) << 1, 0, 0, 0, xc, -xs, 0, xs, xc);
cv::Mat rotY = (cv::Mat_<double>(3, 3) << yc, 0, ys, 0, 1, 0, -ys, 0, yc);
cv::Mat rotZ = (cv::Mat_<double>(3, 3) << zc, -zs, 0, zs, zc, 0, 0, 0, 1);
cv::Mat rotMat;
if (seq == "zyx") rotMat = rotX*rotY*rotZ;
else if (seq == "yzx") rotMat = rotX*rotZ*rotY;
else if (seq == "zxy") rotMat = rotY*rotX*rotZ;
else if (seq == "xzy") rotMat = rotY*rotZ*rotX;
else if (seq == "yxz") rotMat = rotZ*rotX*rotY;
else if (seq == "xyz") rotMat = rotZ*rotY*rotX;
else {
cv::error(cv::Error::StsAssert, "Euler angle sequence string is wrong.",
__FUNCTION__, __FILE__, __LINE__);
}
if (!isRotationMatrix(rotMat)) {
cv::error(cv::Error::StsAssert, "Euler angle can not convert to rotated matrix",
__FUNCTION__, __FILE__, __LINE__);
}
return rotMat;
//cout << isRotationMatrix(rotMat) << endl;
}
/** @brief 四元数转旋转矩阵
* @note 数据类型double; 四元数定义 q = w + x*i + y*j + z*k
* @param q 四元数输入{w,x,y,z}向量
* @return 返回旋转矩阵3*3
*/
cv::Mat quaternionToRotatedMatrix(const cv::Vec4d& q)
{
double w = q[0], x = q[1], y = q[2], z = q[3];
double x2 = x * x, y2 = y * y, z2 = z * z;
double xy = x * y, xz = x * z, yz = y * z;
double wx = w * x, wy = w * y, wz = w * z;
cv::Matx33d res{
1 - 2 * (y2 + z2), 2 * (xy - wz), 2 * (xz + wy),
2 * (xy + wz), 1 - 2 * (x2 + z2), 2 * (yz - wx),
2 * (xz - wy), 2 * (yz + wx), 1 - 2 * (x2 + y2),
};
return cv::Mat(res);
}
/** @brief ((四元数||欧拉角||旋转向量) && 转移向量) -> 4*4 的Rt
* @param m 1*6 || 1*10的矩阵 -> 6 {x,y,z, rx,ry,rz} 10 {x,y,z, qw,qx,qy,qz, rx,ry,rz}
* @param useQuaternion 如果是1*10的矩阵,判断是否使用四元数计算旋转矩阵
* @param seq 如果通过欧拉角计算旋转矩阵,需要指定欧拉角xyz的排列顺序如:"xyz" "zyx" 为空表示旋转向量
*/
cv::Mat attitudeVectorToMatrix(cv::Mat& m,bool useQuaternion, const std::string& seq)
{
CV_Assert(m.total() == 6 || m.total() == 10);
if (m.cols == 1)
m = m.t();
cv::Mat tmp = cv::Mat::eye(4, 4, CV_64FC1);
//如果使用四元数转换成旋转矩阵则读取m矩阵的第第四个成员,读4个数据
if (useQuaternion) // normalized vector, its norm should be 1.
{
cv::Vec4d quaternionVec = m({ 3, 0, 4, 1 });
quaternionToRotatedMatrix(quaternionVec).copyTo(tmp({ 0, 0, 3, 3 }));
// cout << norm(quaternionVec) << endl;
}
else
{
cv::Mat rotVec;
if (m.total() == 6)
rotVec = m({ 3, 0, 3, 1 }); //6
else
rotVec = m({ 7, 0, 3, 1 }); //10
//如果seq为空表示传入的是旋转向量,否则"xyz"的组合表示欧拉角
if (0 == seq.compare(""))
cv::Rodrigues(rotVec, tmp({ 0, 0, 3, 3 }));
else
eulerAngleToRotatedMatrix(rotVec, seq).copyTo(tmp({ 0, 0, 3, 3 }));
}
tmp({ 3, 0, 1, 3 }) = m({ 0, 0, 3, 1 }).t();
//std::swap(m,tmp);
return tmp;
}
int main()
{
//定义手眼标定矩阵
std::vector<Mat> R_gripper2base;
std::vector<Mat> t_gripper2base;
std::vector<Mat> R_target2cam;
std::vector<Mat> t_target2cam;
Mat R_cam2gripper = (Mat_<double>(3, 3));
Mat t_cam2gripper = (Mat_<double>(3, 1));
vector<Mat> images;
size_t num_images =13;//13组手眼标定数据
// 读取末端,标定板的姿态矩阵 4*4
std::vector<cv::Mat> vecHg, vecHc;
cv::Mat Hcg;//定义相机camera到末端grab的位姿矩阵
Mat tempR,tempT;
for (size_t i = 0; i < num_images; i++)//计算标定板位姿
{
cv::Mat tmp = attitudeVectorToMatrix(CalPose.row(i), false,""); //转移向量转旋转矩阵
vecHc.push_back(tmp);
RT2R_T(tmp, tempR, tempT);
R_target2cam.push_back(tempR);
t_target2cam.push_back(tempT);
}
for (size_t i = 0; i < num_images; i++)//计算机械臂位姿
{
cv::Mat tmp = attitudeVectorToMatrix(ToolPose.row(i), false, "xyz"); //机械臂位姿为欧拉角-旋转矩阵
vecHg.push_back(tmp);
RT2R_T(tmp, tempR, tempT);
R_gripper2base.push_back(tempR);
t_gripper2base.push_back(tempT);
}
//手眼标定,CALIB_HAND_EYE_TSAI法为11ms,最快
calibrateHandEye(R_gripper2base, t_gripper2base, R_target2cam, t_target2cam, R_cam2gripper, t_cam2gripper, CALIB_HAND_EYE_TSAI);
Hcg = R_T2RT(R_cam2gripper, t_cam2gripper);//矩阵合并
std::cout << "Hcg 矩阵为: " << std::endl;
std::cout << Hcg << std::endl;
cout<<"是否为旋转矩阵:"<< isRotationMatrix(Hcg) << std::endl << std::endl;//判断是否为旋转矩阵
//Tool_In_Base*Hcg*Cal_In_Cam,用第一组和第二组进行对比验证
cout << "第一组和第二组手眼数据验证:" << endl;
cout << vecHg[0] * Hcg*vecHc[0] << endl << vecHg[1] * Hcg * vecHc[1] << endl << endl;//.inv()
cout << "标定板在相机中的位姿:" << endl;
cout << vecHc[1] << endl;
cout << "手眼系统反演的位姿为:" << endl;
//用手眼系统预测第一组数据中标定板相对相机的位姿,是否与vecHc[1]相同
cout << Hcg.inv()* vecHg[1].inv()* vecHg[0] * Hcg*vecHc[0] << endl << endl;
cout << "----手眼系统测试----" << endl;
cout << "机械臂下标定板XYZ为:" << endl;
for (int i = 0; i < vecHc.size(); ++i)
{
cv::Mat cheesePos{ 0.0,0.0,0.0,1.0 };//4*1矩阵,单独求机械臂下,标定板的xyz
cv::Mat worldPos = vecHg[i] * Hcg*vecHc[i] * cheesePos;
cout << i << ": " << worldPos.t() << endl;
}
getchar();
}
4 程序输出
Hcg 矩阵为:
[0.008453865805544414, -0.9990489305401753, 0.04277577047200548, 0.07638705395676357;
0.01898771468630467, 0.04292996492156131, 0.9988976347968919, -0.08206354381579613;
-0.9997839760888014, -0.007632332432839339, 0.01933258021323825, -0.1311098155037144;
0, 0, 0, 1]
是否为旋转矩阵:1
第一组和第二组手眼数据验证:
[-0.9827262517458556, 0.1843060418844967, 0.01674506059741485, -0.4457787409127387;
0.1838216085000257, 0.9825904904541024, -0.02693592986383497, -0.6886150828753749;
-0.02141799192277936, -0.02339254141892869, -0.9994969027605635, 0.08284331808916068;
0, 0, 0, 1]
[-0.9824787510996111, 0.1850986855040433, 0.0217710877639008, -0.441259542992489;
0.1843694850759817, 0.9823437476322023, -0.03175932084817229, -0.6894248600904512;
-0.02726530048551778, -0.02718893364210982, -0.9992584076588193, 0.08159252779194137;
0, 0, 0, 1]
标定板在相机中的位姿:
[0.8341198940795272, -0.1369737069955237, -0.5343053489276171, -0.01969337858360518;
0.05021760995408052, 0.983511189246883, -0.1737352361401729, -0.05095294728651902;
0.5492924484746335, 0.1180844791582967, 0.8272447411925057, 0.3671266719105768;
0, 0, 0, 1]
手眼系统反演的位姿为:
[0.8373227680667449, -0.1343311553869149, -0.5299487925917564, -0.01514939120843839;
0.05049903955148193, 0.9842033941157671, -0.1696865522526224, -0.05055927730944099;
0.5443715909940763, 0.1153205085985169, 0.8308795046305798, 0.3684833472702467;
0, 0, 0, 1]
----手眼系统测试----
机械臂下标定板XYZ为:
0: [-0.4457787409127387, -0.6886150828753749, 0.08284331808916068, 1]
1: [-0.441259542992489, -0.6894248600904512, 0.08159252779194137, 1]
2: [-0.4422208339914133, -0.6864831180641821, 0.08013587355743718, 1]
3: [-0.4434900953499247, -0.6870035574330987, 0.07976634930332338, 1]
4: [-0.4450797367777684, -0.6874268887433959, 0.08143249774989553, 1]
5: [-0.4418885185926491, -0.6886217895474291, 0.07975714114113902, 1]
6: [-0.4409575603391271, -0.6878847949543246, 0.07934926736540387, 1]
7: [-0.4418588641213109, -0.6896930064251171, 0.08193358154038349, 1]
8: [-0.4437857547008249, -0.6894962022042577, 0.08123334852187797, 1]
9: [-0.4434430428709751, -0.6885152411299985, 0.08092995069314945, 1]
10: [-0.4447502944365486, -0.6878924537730967, 0.08293636801126125, 1]
11: [-0.4422290895104752, -0.6884201696013612, 0.07993373823200106, 1]
12: [-0.4418946218302015, -0.6878072561612861, 0.07990104035206125, 1]
5 数据分析
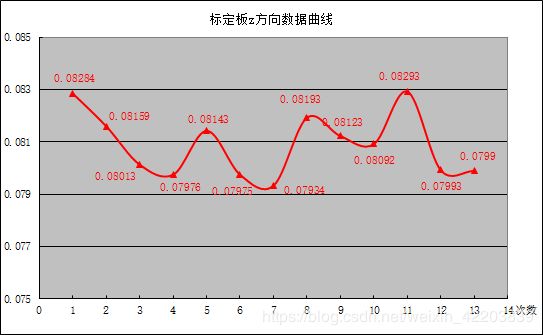
使用excel绘制机械臂坐标系下标定板z方向的数据,获得下图曲线。之后使用excel的STDEV函数求均方差,得到z方向的误差为0.0012042,即±1.2mm的标定误差,满足项目需求。
6 总结
(1)机械臂位姿类型有xyz,zyx,zyz几种,注意区分(可以找机械臂公司问)。
(2)注意弄清楚手眼矩阵的方向!!!
(3)采集标定数据时,标定板拍摄视角尽可能大,如此标定精度更高。
7 其他
后面将进行Opencv4五种方法的性能对比、halcon手眼标定及测试。望大家一起学习交流。
(原创不易。若有用,请左下角点赞,谢谢!)