【文献阅读】Feature Denoising for Improving Adversarial Robustness

论文网址：https://arxiv.org/abs/1812.03411
国内镜像：https://xxx.itp.ac.cn/abs/1812.03411

---

这篇主要解决的是对抗攻击中出现的问题。没有好好研究对抗攻击中具体的算法，就大概知道是怎么回事。

• 对抗攻击：通过对输入添加微小的扰动使得分类器分类错误，一般对用于深度学习的网络的攻击算法最为常见，应用场景包括目前大热的CV和NLP方向，例如，通过对图片添加精心准备的扰动噪声使得分类器分错，或者通过对一个句子中的某些词进行同义词替换使得情感分类错误。

对抗攻击有很多种类，从攻击环境来说，可以分为黑盒攻击，白盒攻击或者灰盒攻击。

• 黑盒攻击：攻击者对攻击的模型的内部结构，训练参数，防御方法（如果加入了防御手段的话）等等一无所知，只能通过输出输出与模型进行交互。
• 白盒攻击：与黑盒模型相反，攻击者对模型一切都可以掌握。目前大多数攻击算法都是白盒攻击。
• 灰盒攻击：介于黑盒攻击和白盒攻击之间，仅仅了解模型的一部分。（例如仅仅拿到模型的输出概率，或者只知道模型结构，但不知道参数）

从攻击的目的来说，可以分为有目标攻击和无目标攻击。

• 无目标攻击：以图片分类为例，攻击者只需要让目标模型对样本分类错误即可，但并不指定分类错成哪一类。
• 有目标攻击：攻击者指定某一类，使得目标模型不仅对样本分类错误并且需要错成指定的类别。从难度上来说，有目标攻击的实现要难于无目标攻击。

从扰动的强度大小来说，可以分为无穷范数攻击，二范数攻击和0范数攻击（下列公式中的x表示的是扰动大小）。
$$\Vert x{\Vert }_p=(\sum _{i=1}^n|x_i{|}^p{)}^{\frac{1}{p}}$$

• 无穷范数攻击：当p趋近于无穷大时，上式子表示扰动中最大的一个，通常在论文里，对于MNIST数据集，限制是（-0.3，0.3）。
• 二范数攻击：p=2
• 0范数攻击（单像素攻击）：此时限制的是可以改变的像素个数，不关心具体每个像素值改变了多少。在MNIST数据集中，一般限制是12个。

从攻击的实现来说来说，可以分为基于梯度的攻击，基于优化的攻击，基于决策面的攻击或者其他。

• 基于梯度的攻击：FGSM（Fast Gradient Sign Method)、PGD(Project Gradient Descent)、MIM(Momentum Iterative Method)
• 基于优化的攻击：CW(Carlini-Wagner Attack)
• 基于决策面的攻击：DEEPFOOL
• 其他：Pointwise

---

这篇文章主要使用的方法是：

用了非局部均值或其他滤波方法对特征图进行降噪

主要贡献结果是：

在ImageNet上，经过10轮的PGD白盒攻击，最先进的算法只有27.9%的正确率，而我们的方法达到了55.7%；经过2000轮的PGD白盒攻击，依旧有42.6%的正确率

---

首先是作者的出发点，观察对抗攻击中生成的“脏”图的特征图以及他本身，可以发现对抗扰动虽然在像素空间中很小，但是会导致网络的特征图中出现大量的“噪声”。
这些干扰要么被认为是人类察觉不到的，要么被认为是不会妨碍人类识别视觉内容的噪音。

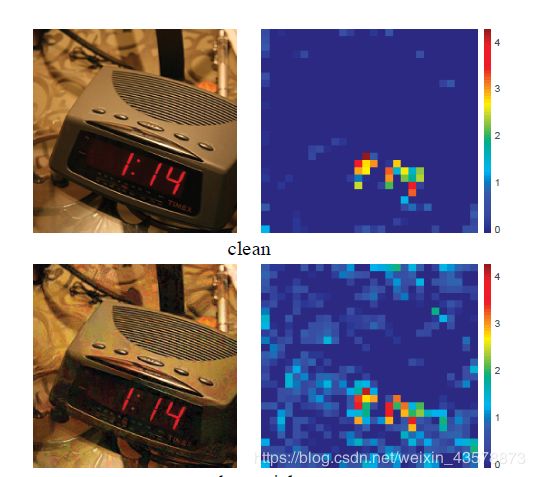
自然而然就会想到对特征图进行降噪，而作者的消融实验表明，使用非局部均值滤波、均值滤波、中值滤波和双边滤波进行特征去噪提高了对抗的鲁棒性，表明特征去噪是一个很好的设计原则。

下图是一个普适的特征图去噪模块：

对应着有四种实例化方式：

1.Non-local means

$$y_i=\frac{1}{C(x)}\sum _{\forall j\in \lambda }f(x_i,x_j)\cdot x_j$$

2.Bilateral filter

$$y_i=\frac{1}{C(x)}\sum _{\forall j\in \Omega (x)}f(x_i,x_j)\cdot x_j$$
双边滤波与非局部均值滤波唯一的不同在于j的取值范围$$\Omega j$$
是一个局部区域（例如3 * 3的patch）。

3.Mean filter

最简单的去噪方法，也可以当作步长为1的平均池化。

4.Median filter

$$y_i=median\{\forall j\in \Omega (i):x_j\}$$

其中
$$f(x_i,x_j)$$
也对应着两种方法：

1.Gaussian(softmax)

$$f(x_i,x_j)=e^{\frac{1}{\sqrt{d}}\theta (x_i{)}^T\varphi (x_j{)}^T}$$
$$C={\sum }_{\forall j\in \lambda }f(x_i,x_j)$$
其中，d是通道的数量。

2.Dot product

$$f(x_i,x_j)=x_i^T{x}_j$$
$$C=N$$
其中，N是总像素数。