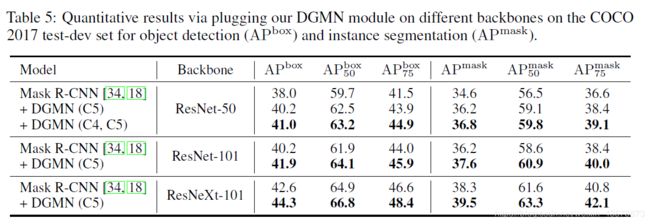
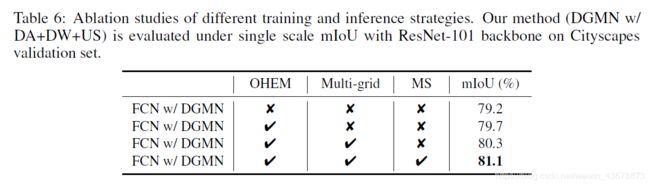
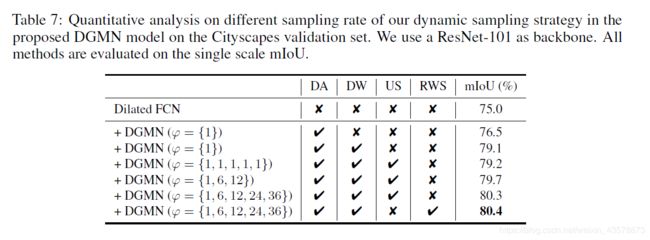
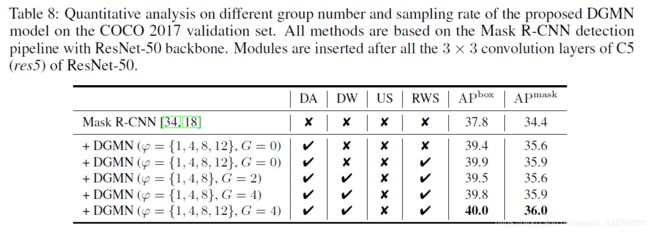
【文献阅读】Dynamic Graph Message Passing Networks
原文链接:https://arxiv.org/abs/1908.06955
尽管cnn在许多计算机视觉任务中表现出色,但它们在捕获长期的结构化关系方面仍然受到限制,因为它们通常由局部kernel层组成。全连接图对这种建模是有益的,但是它的计算开销太大了。所以作者提出了一种基于消息传递神经网络框架的动态图消息传递网络,与建立全连通图的相关工作相比,大大降低了计算复杂度。根据输入条件对图中的节点进行自适应采样来实现的,以便进行消息传递。
Non-local通过学习特征图中所有特征元素之间的两两结构关系,得到用于特征聚合的注意力权重,它将每个特征元素视为图中的一个节点,有效地对一个全连通特征图进行建模,从而使特征元素个数具有二次推理复杂度 O ( N 2 ) O(N^2) O(N2)。但是,这对于高分辨率图像上的密集预测任务是不可行的;此外,在密集预测任务中,由于信息冗余,通常不需要捕获所有像素对之间的关系。
图卷积网络(Graph convolution networks, GCNs)可以将信息沿图结构输入数据传播,在一定程度上缓解了非局部网络的计算问题。但是,只有在为每个节点考虑局部邻域时才会出现这种情况。
针对上述问题,作者提出了一种新的动态图消息传递网络,基于通用消息传递神经网络框架的深度表征学习(DGMN)模型。

该模型具有两个关键的动态特性:
- 根据输入条件对节点的邻域进行动态采样,直观地说,这允许网络仅通过选择图中最相关节点的一个子集来有效地收集远程上下文
- 基于已采样的节点,进一步动态预测基于节点条件的过滤权重和关联矩阵,这些权重和关联矩阵用于通过消息传递在特征节点之间传播信息
1. 问题定义和符号
给定一个特征图,并将分解为一组特征向量 F = { f i } i = 1 N F=\{f_{i}\}_{i=1}^{N} F={fi}i=1N,其中 f i ∈ R 1 × C f_{i} \in \mathbb{R}^{1 \times C} fi∈R1×C, N N N是像素的数目,C是特征维度。
目标是通过利用隐藏在不同像素位置的特征向量之间的结构化信息学习一组潜在特征向量 H = { h i } i = 1 N H=\{ h_{i} \} _{i=1} ^{N} H={hi}i=1N, H H H的维数和 F F F的维数相同。
为了学习这种结构化表示,通过构造一个feature graph, G = { V , ε , A } G=\{V,\varepsilon, A\} G={V,ε,A},其中 V V V是节点, ε \varepsilon ε是边, A A A是邻接矩阵。具体来说,图的节点由潜在特征向量表示, V = { h i } i = 1 N V=\{ h_{i} \} _{i=1} ^{N} V={hi}i=1N;带有描述节点间连接的二进制或可学习的邻接矩阵 A ∈ R N × N A\in \mathbb{R}^{N \times N} A∈RN×N。
2. 图信息传递神经网络
消息传递阶段通常采用 T T T迭代步骤来更新特征节点,而读出阶段用于网络预测。
消息传递阶段包含两个步骤,分别是消息计算 M T M^{T} MT 和消息更新 U T U^{T} UT。
给定一个 t t t时刻的潜在特征向量 h i T h_{i}^{T} hiT,考虑一个局部连接节点域 v i ⊂ V v_{i} \subset V vi⊂V, v i ∈ R ( K × C ) v_{i} \in \mathbb{R}^{(K \times C)} vi∈R(K×C), K ≪ N K \ll N K≪N。
节点 i i i的消息计算公式如下:
m i ( t + 1 ) = M t ( A i , j , { h 1 t , ⋯ , h K t } , w j ) = ∑ j ∈ N ( i ) A i , j h j t w j , w i t h A i , j = A [ i , j ] m_{i}^{(t+1)}=M^{t}(A_{i,j},\{h_{1}^{t}, \cdots,h_{K}^{t}\}, w_{j}) = \sum_{j \in N(i)}A_{i,j}h_{j}^{t}w_{j}, \space with \space A_{i,j}=A[i,j] mi(t+1)=Mt(Ai,j,{h1t,⋯,hKt},wj)=j∈N(i)∑Ai,jhjtwj, with Ai,j=A[i,j]
其中, A i , j A_{i,j} Ai,j描述了 h i ( t ) h_{i}^{(t)} hi(t)和 h j ( t ) h_{j}^{(t)} hj(t)间的关系; N ( i ) N(i) N(i)表示节点 h i ( t ) h_{i}^{(t)} hi(t)的自包含邻域,可由 v i v_i vi导出; w j ∈ R C × C w_{j} \in \mathbb{R}^{C \times C} wj∈RC×C是一个用于 h j ( t ) h_{j}^{(t)} hj(t)上消息计算的变换矩阵。
然后利用消息更新函数 U t U^t Ut对节点 h i h_{i} hi进行更新,将计算得到的消息与节点 i i i处的观测特征 f i f_i fi线性组合为:
h i ( t + 1 ) = U t ( f i , m i ( t + 1 ) ) = σ ( f i + α i m m i ( t + 1 ) ) h_{i}^{(t+1)}=U^t(f_i,m_i^{(t+1)})=\sigma(f_i+\alpha_{i}^m m_i^{(t+1)}) hi(t+1)=Ut(fi,mi(t+1))=σ(fi+αimmi(t+1))
其中, α i m \alpha_i^{m} αim是一个可学习的用于缩放信息的参数; σ ( ⋅ ) \sigma(\cdot) σ(⋅)是非线性函数,比如 R e L U ReLU ReLU。
通过每个节点上迭代执行消息传递 T T T次,就获得了一个细化的特征映射 H ( T ) H^{(T)} H(T)作为输出。
3. 从全连通图到动态采样图
为了有效地减少全连通图的冗余,提出了均匀采样方案和随机游走采样方案。
均匀采样
均匀采样是基于蒙特卡罗估计的图节点采样的一种常用策略。
为了估计 V V V的分布,考虑一组 S S S个均匀采样率 φ \varphi φ, φ = { ρ q } q = 1 S \varphi=\{\rho_q\}_{q=1}^S φ={ρq}q=1S, ρ q \rho_q ρq是采样率。
潜在特征分布在 P P P维空间 R P \mathbb{R}^P RP,图像中 P = 2 P=2 P=2。对于每个潜在节点 h i h_i hi,从 R P \mathbb{R}^P RP中共采样 K K K个邻近节点。因此, v i v_i vi的感受野由 ρ q \rho_q ρq和 K K K决定。
由于 S , K ≪ N S,K \ll N S,K≪N且 S ∗ K ≪ N S * K \ll N S∗K≪N,所以可以保持少量的连接节点,因此可以实现更低的计算开销。
每个节点从不同的接收域(采样率)接收 S S S个信息进行更新:
m i ( t + 1 ) = ∑ q ∑ j ∈ N q ( i ) β q A i , j q h j t w j q , w i t h A i , j q = A q [ i , j ] a n d q = 1 , ⋯ , S m_i^{(t+1)}=\sum_q \sum_{j\in N_q(i)} \beta_q A_{i,j}^q h_j^t w_j^q, \space with \space A_{i,j}^q=A^q[i,j] \space and \space q=1,\cdots,S mi(t+1)=q∑j∈Nq(i)∑βqAi,jqhjtwjq, with Ai,jq=Aq[i,j] and q=1,⋯,S
其中, β q \beta_q βq是来自 q − t h q-th q−th采样率的消息的加权参数; A q A^q Aq表示在采样率 ρ q \rho_q ρq下形成的邻接矩阵; A i , j q , w j q , N q ( i ) A_{i,j}^q,w_j^q,N_q(i) Ai,jq,wjq,Nq(i)同理。
均匀采样方案是一种基于空间分布的线性采样器,没有考虑隐藏节点的原始特征分布,即采样不取决于节点的特征。
随机游走采样
为了在采样时考虑特征数据分布,在均匀采样之上提出了随机游走采样策略。在均匀采样的节点附近游走是一种非线性的、自适应的采样方法,可以促进更好的学习到原始特征分布。

这里的“随机”指的是用随机梯度下降的数据驱动方式来预测 w a l k s walks walks。
给定一组在采样率 ρ q \rho_q ρq下的均匀采样节点 v i q ∈ R K × C v_i^q \in \mathbb{R}^{K \times C} viq∈RK×C,根据采样节点集的特征数据,进一步估计每个节点的随机游走。
在 P P P维空间中,以 Δ d j q ∈ R P × 1 \Delta d_j^q \in \mathbb{R}^{P \times 1} Δdjq∈RP×1来表示一个均匀采样节点 h j , w i t h j ∈ N q ( i ) h_j, \space with \space j\in N_q{(i)} hj, with j∈Nq(i)的游走:
Δ d j q = W i , j q v i q + b i , j q \Delta d_j^q=W_{i,j}^q v_i^q+b_{i,j}^q Δdjq=Wi,jqviq+bi,jq
其中, W i , j q ∈ R P × ( K × C ) W_{i,j}^q \in \mathbb{R}^{P \times (K \times C)} Wi,jq∈RP×(K×C)和 b i , j q ∈ R P × 1 b_{i,j}^q \in \mathbb{R}^{P \times 1} bi,jq∈RP×1是矩阵变换的参数,对每个节点 v i q v_i^q viq是单独学习的。
有了学习到的游走,就可以获得一组新的自适应的采样节点 v i ′ q v_i^{'q} vi′q,并且生成相应的邻接矩阵 A ′ q A^{'q} A′q,消息计算公式就变为:
m i ( t + 1 ) = ∑ q ∑ j ∈ N q ( i ) β q A i , j ′ q ϱ ( h j ′ ( t ) ∣ V , j , Δ d j q ) w j q , w i t h A i , j ′ q = A ′ q [ i , j ] m_i^{(t+1)}=\sum_q \sum_{j \in N_q (i)} \beta_q A_{i,j}^{'q} \varrho(h_j^{'(t)} | V, j, \Delta d_j^q)w_j^q,\space with \space A_{i,j}^{'q}=A^{'q}[i,j] mi(t+1)=q∑j∈Nq(i)∑βqAi,j′qϱ(hj′(t)∣V,j,Δdjq)wjq, with Ai,j′q=A′q[i,j]
其中, ϱ ( ⋅ ) \varrho(\cdot) ϱ(⋅)是双线性采样器,是用来在 h j ( t ) h_j^{(t)} hj(t)附近用预测的游走 Δ d j q \Delta d_j^q Δdjq采样新的特征节点 h j ′ ( t ) h_j^{'(t)} hj′(t),得到新的图节点 V V V。
4. 联合学习动态滤波器和关联度
在消息计算公式中,权值 { w j q } j = 1 K \{w_j^q\}_{j=1}^K {wjq}j=1K对每一个自适应采样节点 v i ′ q v_i^{'q} vi′q是共享的。但是,由于每个 v i ′ q v_i^{'q} vi′q本质上定义了一个特定于节点的局部特征上下文,因此更有意义的做法是使用一个基于节点条件的滤波器来学习每个隐藏节点的消息。除此之外,任意一对节点 h i ( t ) h_i^{(t)} hi(t)和 h j ( t ) h_j^{(t)} hj(t)的亲和度 A i , j ′ A_{i,j}^{'} Ai,j′,也应该以节点 v i ′ q v_i^{'q} vi′q为条件,因为亲和度只对在 v i ′ q v_i^{'q} vi′q中传递的消息进行重新加权。
因此,可以在 v i ′ q v_i^{'q} vi′q上用矩阵变换来同时预测动态的滤波器和动态的亲和度:
{ w j q , A i , j ′ q } = W i , j k , A v i ′ q + b i , j k , A \{w_j^q,A_{i,j}^{'q}\}=W_{i,j}^{k,A} v_{i}^{'q}+b_{i,j}^{k,A} {wjq,Ai,j′q}=Wi,jk,Avi′q+bi,jk,A
A i , j ′ q = s o f t m a x c ( A i , j ′ q ) = e x p ( A i , j ′ q ) ∑ l ∈ N q ( i ) e x p ( A i , j ′ q ) A_{i,j}^{'q}=softmax_c(A_{i,j}^{'q})=\frac{exp(A_{i,j}^{'q})}{\sum_{l \in N_q(i)}exp(A_{i,j}^{'q})} Ai,j′q=softmaxc(Ai,j′q)=∑l∈Nq(i)exp(Ai,j′q)exp(Ai,j′q)
其中, s o f t m a x c ( ⋅ ) softmax_c(\cdot) softmaxc(⋅)是通道维度上的 s o f t m a x softmax softmax操作,用来归一化亲和度 A i , j ′ q ∈ R 1 A_{i,j}^{'q}\in \mathbb{R}^1 Ai,j′q∈R1; W i , j k , A ∈ R ( G × C + 1 ) × ( K × C ) W_{i,j}^{k,A}\in \mathbb{R}^{(G \times C + 1) \times (K \times C)} Wi,jk,A∈R(G×C+1)×(K×C)和 b i , j k , A ∈ R ( G × C + 1 ) b_{i,j}^{k,A}\in \mathbb{R}^{(G \times C + 1)} bi,jk,A∈R(G×C+1)是矩阵变换参数;为了减少参数,使用分组卷积,将 C C C个特征通道分为 G G G组, G ≪ C G \ll C G≪C,每组 C / G C /G C/G个特征通道共享相同的滤波器参数。
网络设计
DGMN(Dynamic Graph Message passing Network)
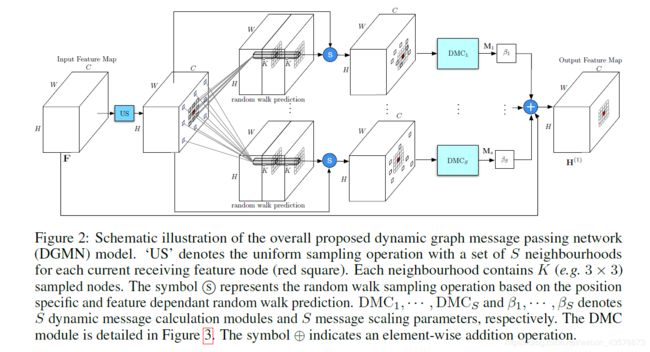
特征图 F F F作为输入, H ( 0 ) H^{(0)} H(0)是潜在特征图 H H H的初始状态,用 F F F来初始化。 H H H和 F F F维度相同, F , H ∈ R H × W × C F,H \in \mathbb{R}^{H \times W \times C} F,H∈RH×W×C。
设置 S S S个均匀采样率(图中为2个采样率的示意),均匀和随机游走从全图采样一些节点,并且返回节点的索引给后面的动态信息计算(DMC)模块使用。估计随机游走节点的变换矩阵 W i , j q W_{i,j}^q Wi,jq用的 3 × 3 3 \times 3 3×3卷积。如果不采用随机游走采样,则将均匀采样的特征节点直接输入动态消息计算模块(DMC)。
利用矩阵乘法计算 q − t h q-th q−th采样率对应的消息 M q ∈ R H × W × C M_q \in \mathbb{R}^{H \times W \times C} Mq∈RH×W×C,缩放与观测特征图 F F F进行线性组合,得到细化的特征图 H ( 1 ) H^{(1)} H(1)作为输出。
为了平衡效果与效率,设置 T = 1 T=1 T=1。
DMC模块(Dynamic Message Calculation)
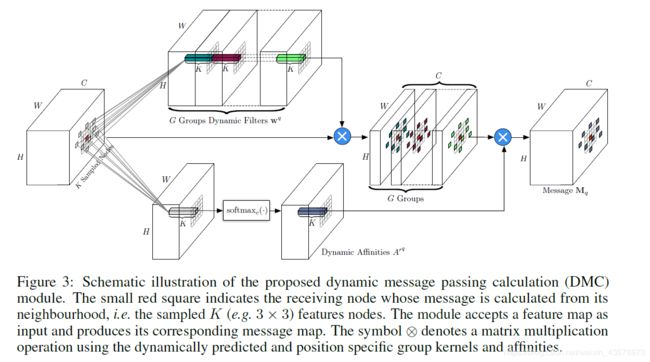
两条数据路径来处理被采样的特征节点:一条预测动态亲和度 A ′ q ∈ R H × W × K A^{'q} \in \mathbb{R}^{H \times W \times K} A′q∈RH×W×K;另一条预测动态滤波器 w q ∈ R H × W × K × G w^q \in \mathbb{R}^{H \times W \times K \times G} wq∈RH×W×K×G, K K K( 3 × 3 3 \times 3 3×3)是卷积核大小, G = 4 G=4 G=4是分组。
用来共同预测动态滤波器和动态亲和度的矩阵变换 W i , j k , A W_{i,j}^{k,A} Wi,jk,A是 3 × 3 3 \times 3 3×3卷积。