【文献阅读】Adaptive Pyramid Context Network for Semantic Segmentation

原文链接：http://openaccess.thecvf.com/content_CVPR_2019/papers/He_Adaptive_Pyramid_Context_Network_for_Semantic_Segmentation_CVPR_2019_paper.pdf

---

近年来的研究表明，上下文特征可以显著地提高深层语义分割分网络的性能。当前基于语义的方法在如何构建语义结构存在着很大的差异。本文首先介绍了上下文特征在分割任务中的三个理想性质。特别地，全局导向的局部亲和力(Global-guided Local Affinity, GLA)在有效语义特征的构建中起着至关重要的作用，而这一特性在以往的研究中一直被忽视。在此基础上，本文提出了自适应金字塔上下文网络(Adaptive Pyramid Context Network, APCNet)来进行语义分割。APCNet采用多个设计良好的自适应上下文模块(Adaptive Context Modules, ACMs)自适应地构造多尺度上下文表示。具体来说，每个ACM利用全局图像作为指导来估计每个子区域的局部亲和系数，然后使用这些亲和度计算上下文向量。

由于CNN的卷积性质，局部卷积特征通常接受域有限。而且，即使接受域很大，这些特征也主要描述核心区域，很大程度上忽略了边界周围的语义。另一方面，来自不同类别的局部区域可能会共享附近的特征，例如木桌和椅子可能会表现出相似的局部纹理。精确的语义分割往往需要来自不同尺度和较大区域的上下文信息来消除局部区域造成的歧义。

所以有一个很自然的问题，什么是语义分割的最佳上下文？

1. Multi-scale（多尺度）
2. Adaptive（自适应）
3. Global-guided Local Affinity（全局指导的局部亲和度）
   

---

方法

公式表示

给定一张图片$I$，用CNN提取特征$X$，$X_i$表示位置$i$处的特征向量，$x_i$表示位置$i$处降维后的特征向量。
一个直接想法是仅使用局部特征$X_i$来估计语义标签，但是这种思想忽略了其他区域的相关内容，限制了分割性能。

引入$z_i=F_{context}(X,i)$来表示$X_i$的上下文特征向量，其中$F_{context}$表示从位置$i$的输入特征立方体中提取$z_i$的函数。以前的上下文分割方法在如何定义$F_{context}$方面各不相同。

首先将$X$变换成多尺度的金字塔表示，然后分别为每个尺度自适应地构造上下文向量。以尺度$s$为例，划分特征图$X$为$s\times s$个子区域，从而将$X$变换成一组子区域表示$Y^s=[Y_1^s,Y_2^s,\cdots ,Y_{s\times s}^s]$。对每个子区域$Y_j^s$，用一个平均池化和一个卷积操作的特征向量$y_j^s$来概括它的内容。引入亲和度系数${\alpha }_{i,j}^s$来表示子区域$Y_j^s$对$X_i$的语义标签估计的贡献程度。所以自适应上下文向量可以表示为
$$z_i^s=\sum _{j=1}^{s\times s}{\alpha }_{ij}^s{y}_j^s$$
关键问题在于如何计算系数${\alpha }_{i,j}^s$。理想情况下，在给定尺度$s$和位置$j$时，${\alpha }_{i,j}^s$通过同时考虑局部特征$x_i$和$X$的全局表示来满足GLA属性。用$g(X)$表示全局信息，$g$是全局信息提取器，${\alpha }_{i,j}^s=f_s(x_i,g(X),j)$，则上式可表示为
$$z_i^s=\sum _{j=1}^{s\times s}{f}_s(x_i,g(X),j)y_j^s$$

Adaptive Context Module（ACM）

ACM包含两个分支，第一个分支用于计算亲和度系数${\alpha }^s$；第二个分支用于处理单一尺度的$y^s$。

首先将$X$用$1\times 1$卷积得到特征降维后的$x$，接着用全局平均池化和一个$1\times 1$卷积获得全局信息特征$g(X)$。
整合局部特征$\{x_i\}$和全局向量$g(X)$来计算每个位置$i$的GLA，具体实现为用$1\times 1$卷积接$sigmoid$激活函数。
每个亲和度向量的维数为$s\times s$，对应于该尺度下的子区域数。最后我们获得$h\ast w$个亲和度向量，将他$reshape$为$hw\times s^2$。

第二个分支使用自适应平均池化和$1\times 1$卷积获得$y^s\in {\mathbb{R}}^{s\times s\times 512}$，然后将$y^s$ $reshape$ 为$s^2\times 512$以匹配亲和度图。

将两个分支最终得到的结果相乘，并且通过$reshape$获得由$\{z_i^s\}$组成的自适应上下文矩阵$z^s$。使用残差结构，在$z_s$中加上输入$x$。

Adaptive Pyramid Context Network（APCNet）

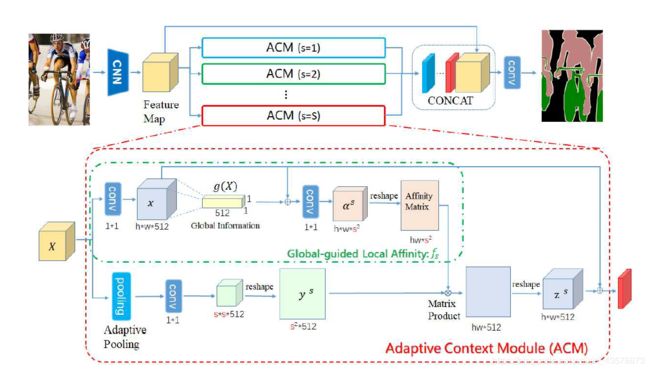
先用CNN提取特征，将得到的特征图$X$转变为有$S$个尺度的金字塔。对于每个尺度$s$来说，利用自适应平均池化和$1\times 1$卷积将$X$转变为特定的空间尺寸$s\times s$并且得到$y^s\in {\mathbb{R}}^{s\times s\times c}$。送入ACM中得到自适应上下文向量$z_i^s$，将不同尺度的$\{z_i^s\}$ $concat$得到$z_i=[z_i^1,z_i^2,\cdots ,z_i^S]$。最后利用局部特征$\{X_i\}$和上下文向量$\{z_i\}$来预测每个像素的语义标签。

---

实验结果