自动驾驶路径规划技术-高速公路路径规划
Path Planning - Highway Driving project
Github: https://github.com/williamhyin/CarND-Path-Planning
Email: [email protected]
知乎专栏: 自动驾驶全栈工程师
Overview
在自动驾驶流程管道中, 我们按顺序处理以下模块:
- 感知: 负责使用传感器探测对象
- 融合: 负责使用传感器融合提供被检测物体的综合视图
- 定位: 负责确定自身车辆所在的位置, 尤其需要精确到在车道中的具体位置
- 路径规划: 负责规划车辆轨迹达到一个特定的目标
- 指挥与控制: 以规划的路径作为输入, 控制驱动车辆
路径规划模块的输入包括:
- 传感器融合的对象列表
- 地图和定位系统
路径规划模块的输出是一组路径点.
路径规划模块通常分解为以下一组子模块:
- 预测(Predictions): 预测周围被探测物体的轨迹
- 行为规划器(Behavior planner): 将定义一组候选的高层级目标, 让车辆跟随(车道变化, 减速…)
- 轨迹生成器(Trajectories planner): 对于每一个可能的高级目标, 都会计算出一条可以跟踪的路径
- 轨迹成本排序(Trajectories cost ranking): 对于每个轨迹, 成本将被推导出来(取决于可行性、安全性、合法性、舒适性和效率) , 最低总成本的轨迹将被选择
Details
预测(Predictions)
预测工作非常有趣, 但是极富挑战, 因为预测本身是多模的, 即存在多个不同概率分布的可能性. 首先预测模块会输入地图数据和传感器融合数据, 然后预测模块会生成并输出一些预测数据. 这些预测数据包含了周围所有其他机动车以及其他移动物体的未来状态. 为了更清楚地说明这一点, 本文结尾Backup有一个示例(json 格式) , 说明预测的输入和输出可能是什么样的. 实际的预测会延伸到10-20s的范围.
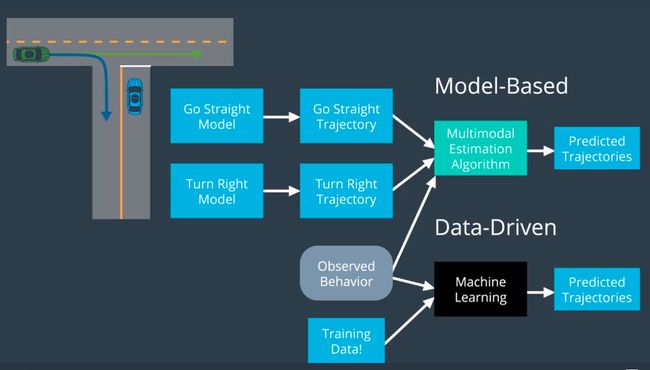
预测有两种方式:Model-base / Data-driven Approaches
两种预测方式的对比
在基于模型的方法中, 我们将使用一些简单的轨迹生成器来绘出当驾驶员直行或者右转时的我们的预测轨迹. 然后我们将注意力放在目标车辆的实际行为上, 并使用当前还是个黑盒子的多模估量算法, 我们将对比观察的轨迹和每个模块中我们预期生成的轨迹, 并为每一条可能的轨迹赋予一个几率.
在数据驱动的方法中, 我们就有了一个真正的黑盒算法, 该算法会通过大量训练数据来训练. 一旦训练完成, 我们会把观察到的行为输入其中, 让算法来生成接下来如何运动的预测. 比如每个不同的时段在一个交叉路口的车辆的不同行为.
基于模型的方法需要我们为每种行为建立了运动数学模型, 并将司机行为的理解, 目标车辆的物理限制, 交通路规以及其他限制考虑在内. 数据驱动法使用数据来抽取潜在模式, 这是基于模型法所缺少的. 但是数据驱动的算法使用历史的数据预测未来的情况, 并没有考虑车辆物理学和交通规律.
-
Data-driven Approaches: 数据驱动法则依赖于机器学习和案例学习
-
example: trajectory clustering
目前有很多机器学习的算法来预测对象的轨迹, 他们大多数都是为了实现轨迹聚合(trajectory clustering). 算法分为两个阶段. 第一个是离线训练阶段, 在此阶段中, 算法从数据中学习模式, 第二个阶段是在线预测阶段, 在此阶段中, 算法使用模型来生成预测.
在离线阶段, 这个阶段的目标是给一些机器学习算法提供大量的数据来训练它. 可以通过如在交通路口放置一个固定摄像头实现, 清理数据之后会得到很多轨迹. 通过相似性测量可以减少很多轨迹, 最后通过聚类算来聚合这些轨迹. 最后定义原型运动路径.
主要包括这三步:
- 定义相似性- 我们首先需要一个与人类常识定义相一致的相似性定义.
- 无监督的聚类- 在这一步, 一些机器学习算法对我们已经观察到的轨迹进行聚类.
- 确定原型轨迹- 为每个集群确定一些少数典型的“原型”轨迹.
在在线阶段, 需要观察车辆的部分路径, 并使用相似性检测对比原型轨迹, 最后预测未来的轨迹. 在轨迹的初始时间阶段(如在红绿灯前), 不同原型轨迹的概率是相同的, 我们为每个聚合选择最匹配的原型轨迹, 并使用它们来代表车辆的未来轨迹. 随着车辆继续右转, 自身车辆的轨迹与右转原型轨迹越来越契合, 红色聚合对应的可能性快速接近1.
主要包括这三步:
- 观察部分轨迹- 当目标车辆行驶时, 我们可以想象它在后面留下了一个“部分轨迹”.
- 比较原型轨迹- 我们可以比较这个部分轨迹与原型轨迹的相应部分. 当这些部分轨迹更加相似时(使用前面定义的相似概念) , 它们相对于其他轨迹的可能性会增加.
- 生成预测- 对于每个集群, 我们确定最可能的原型轨迹. 我们将这些轨迹连同相关概率一起广播(见下图).
在线检测
-
-
Model-based Approaches: 基于模型法使用运动数学模型来预测运动轨迹
基于模型的方法, 首先对于每个目标, 识别在当前状态下目标的下一步所有可能的行为. 然后为每种行为定义一个过程模型. 行为对应的过程模型就是用数学方式把行为相关的物体移动描述出来, 它是一个函数, 可以用来计算一段时间结束后的物体状态, 从时间t开始到t+1结束. 过程模型会产生一些的不确定状态, 在定义过程模型后可以使用过程模型来计算每种行为的几率大小. 具体计算过程需要获取时间点t-1上的目标状态观察值, 然后运行过程模型计算t时间点的预期状态, 然后将在时间点t的物体实际观测状态与过程模型之前的预测状态进行比较, 使用多模估量算法来过得每种可能动作的几率. 最后为每种行为预测一个轨迹, 通过在过程模型上进行迭代直到预测时间段的结束点就行.
基于模型的方法
你也可以将基于模型的预测问题解决方案看作也具有“离线”和在线部分:
-
定义过程模型(离线)
-
使用过程模型来比较驾驶员行为和我们每个模型所预计的行为
-
通过使用多模算法比较不同行为的可能性来概率的分类驾驶员的意图
-
推算过程模型来生成路径
-
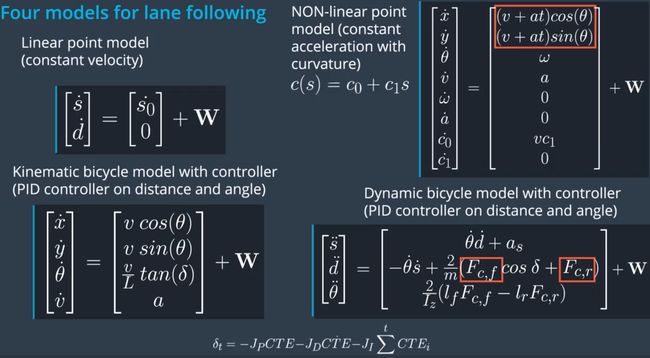
Defining Process models: 使用过程模型的数学技术, 来模型化不同的动作, 比如车道变换和跟随驾驶等
过程模型
我们需要用一些数学公式来表示这些模型:
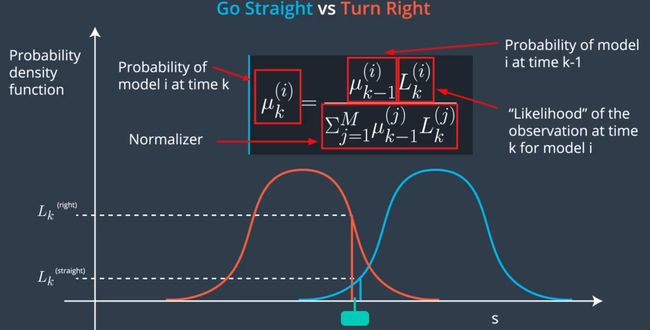
- Using Process Models:过程模型首先用于比较目标车辆的观察行为和我们为每个演习创建的模型所期望的行为. 下面的图片有助于解释过程模型是如何用来计算这些可能性的.
假设在一个路口有直行和右转两种行为. 我们现在时间点k-1上观察车辆状态, 然后再在时间点k上观察, 为了基于新的观察值来计算新的行为概率, 我们会从时间点k-1时候的状态出发来运行两个过程模型, 我们在时间点k得到两种预期状态, 我们可以在上图看到这两宗预期状态的坐标分布. 这个结果是通过对每个模型的观察值进行可能性度量得到. 而通过上图中的函数我们可以计算每个模型在t时刻点的概率. 很明显在这个路口车辆更像是右转.
- Classifying Intent with Multiple Model Algorithm: 使用多模估量器来处理维护预测伴随的不确定性, 也就是说在特定情况下, 目标将做何种动作的几率. 在本节顶部的图像中, 您可以看到一个条形图, 表示随着时间的推移各种集群的概率. 对于基于模型的方法, 多模型算法有着相似的用途: 它们负责维护每次机动概率的信念. 我们讨论的算法被称为自治多模型算法(AMM-Autonomous multiple model algorithm).
变量M代表过程模型数或者行为数, μk(i)代表某种行为的几率大小.
- Trajectory Generation: 一旦我们有了一个过程模型, 轨迹生成就很简单了. 我们只是一遍又一遍地重复我们的模型, 直到我们生成了一个预测, 它跨越了我们应该覆盖的任何时间范围. 注意, 过程模型的每次迭代都必然会给我们的预测增加不确定性.
-
-
Hybrid Approaches: 使用数据和过程模型来预测运动
我们可以将基于模型方法中的多模预测器使用机器学习算法替换, 如Naive Bayes:


-
Intent Classification: 预测过程通过一个密集计算的分类循环完成, 该循环的主要工作是预测司机的动向并生成轨迹
-
Naive Bayes: 预测汽车如何运动(如在T型路口)
高斯朴素贝利叶是指假设独特的特征变量的概率具有高斯分布
朴素贝叶斯的部分实施代码:
string GNB::predict(const vector&sample) { /** * Once trained, this method is called and expected to return * a predicted behavior for the given observation. * @param observation - a 4 tuple with s, d, s_dot, d_dot. * - Example: [3.5, 0.1, 8.5, -0.2] * @output A label representing the best guess of the classifier. Can * be one of "left", "keep" or "right". * * TODO: Complete this function to return your classifier's prediction */ // Calculate product of conditional probabilities for each label. double left_p = 1.0; double keep_p = 1.0; double right_p = 1.0; for (int i=0; i<4; ++i) { left_p *= (1.0/sqrt(2.0 * M_PI * pow(left_sds[i], 2))) * exp(-0.5*pow(sample[i] - left_means[i], 2)/pow(left_sds[i], 2)); keep_p *= (1.0/sqrt(2.0 * M_PI * pow(keep_sds[i], 2))) * exp(-0.5*pow(sample[i] - keep_means[i], 2)/pow(keep_sds[i], 2)); right_p *= (1.0/sqrt(2.0 * M_PI * pow(right_sds[i], 2))) * exp(-0.5*pow(sample[i] - right_means[i], 2)/pow(right_sds[i], 2)); } // Multiply each by the prior left_p *= left_prior; keep_p *= keep_prior; right_p *= right_prior; double probs[3] = {left_p, keep_p, right_p}; double max = left_p; double max_index = 0; for (int i=1; i<3; ++i) { if (probs[i] > max) { max = probs[i]; max_index = i; } } return this -> possible_labels[max_index]; } 值得注意的是, 在真实的轨迹预测往往需要同时预测多个对象的运动
-
行为规划器(Behavior planner)
行为规划部分决定了车辆在任何时候应该表现出什么样的行为. 例如, 在交通信号灯或十字路口停车、改变车道、加速或左转进入一条新的街道都是这个组件可能发出的操作.
行为规划器根据行为规划师的建议, 输入地图、路线和其他车辆可能会做的预测, 并建议轨迹模块来创建轨迹.
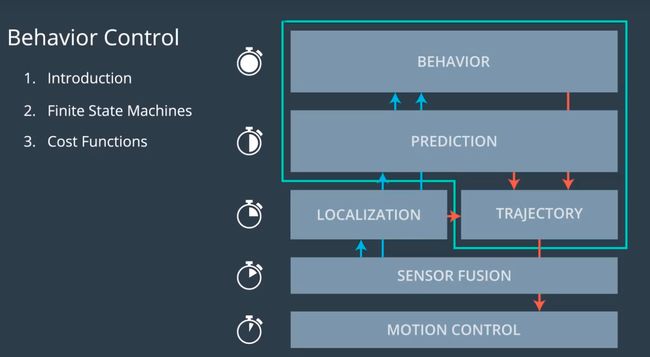
行为规划的概览
由于行为规划需要获取大量数据然后才能做出决策, 因此整个过程需要更长的时间. 但是如果等待行为模块反应, 那么它将会阻塞整个循环管线, 影响下游模块. 为了解决时间调度的问题, 正确做法是使用现有数据, 并接受这些数据并非最新数据的事实.
-
有限状态机是一种实现行为规划的技术.
通过只指定几个数量, 就可以建议多种多样的行为. 例如, 通过只指定目标车道、目标车辆(跟随)、目标速度和到达这些目标的时间, 我们可以通过下面的Json了解行为规划的输出.
{
"target_lane_id" : 2,
"target_leading_vehicle_id": 2,
"target_speed" : 15.0,
"seconds_to_reach_target" : 5.0,
}
有限状态机基于有限的离散状态来做决策,
有限状态机是一个非常简单的抽象反应系统,因为它只针对特定的外界输入产生数量有限的相应。
其核心思想是,通过有限的状态描述定义,组合产生大量的复杂的逻辑行为。
一个有限状态机通常包括,输入集合,输出集合,转换逻辑;每个状态机根据是否有输出可以分为两类,接收器(Acceptor)和变换器(Transducer). 在高速道路行驶场景中,可以用5个状态来组合表达无人车的所有可能驾驶动作。
自动驾驶有限状态机(状态定义)
-
转换函数
决定自动驾驶状态如何转换以及转换函数的输入对于有限状态机的实现非常重要. 预测结果, 地图, 速度限制, 定位信息以及当前状态都需要作为转换函数的输入传递到有限状态机.
以下是行为规划的伪代码:
def transition_function(predictions, current_fsm_state, current_pose, cost_functions, weights):
# only consider states which can be reached from current FSM state.
possible_successor_states = successor_states(current_fsm_state)
# keep track of the total cost of each state.
costs = []
for state in possible_successor_states:
# generate a rough idea of what trajectory we would
# follow IF we chose this state.
trajectory_for_state = generate_trajectory(state, current_pose, predictions)
# calculate the "cost" associated with that trajectory.
cost_for_state = 0
for i in range(len(cost_functions)) :
# apply each cost function to the generated trajectory
cost_function = cost_functions[i]
cost_for_cost_function = cost_function(trajectory_for_state, predictions)
# multiply the cost by the associated weight
weight = weights[i]
cost_for_state += weight * cost_for_cost_function
costs.append({'state' : state, 'cost' : cost_for_state})
# Find the minimum cost state.
best_next_state = None
min_cost = 9999999
for i in range(len(possible_successor_states)):
state = possible_successor_states[i]
cost = costs[i]
if cost < min_cost:
min_cost = cost
best_next_state = state
return best_next_state
-
成本函数
驾驶策略通常由成本函数定义. 成本函数可以对行为做出正确评估. 它可以调整为非常保守的驾驶体验(与前面的车辆保持相当大的安全距离, 只有在目标车道上有大量空闲空间时才改变车道… …)或者它可以调整为更快的驾驶体验(尽可能多地改变车道以尽可能快地驾驶… …). 定义了不同成本函数后, 我们可以真正做出行为级别的决策.
在我的实现中, 行为规划器不是像车道变更那样马上做出决定, 而是定义了几个可能的目标. 将由成本函数根据其适用性选择最佳决策: 即根据对所生成轨迹的成本函数评估.
如何为车速设计成本函数:
以下是成本函数的一个实例, 我们一方面想尽快到达目的地,一方面又不能超速,需要的控制量就是汽车的期望车速,假设成本函数值是(0~1)之间,且成本函数是线性的,通过调整成本函数的权重,从而调节成本函数的相对重要性, 我们可以通过成本函数计算不同速度下的成本.
设计成本函数是比较困难的工作, 而将他们组合起来生成可用的车辆行为则是非常困难的工作.
一方面我们解决新问题的时候, 很可能带入已经工作的很好的原有模块中, 导致原有模块出错.
另一个困难是如何去平衡各种目标量之间的冲突. 最后为不同的目标量定义不同的成本函数, 选择合适的成本参数.
下图是高速公路场景成本函数的实例, 在不同的场景下需要定义不同的成本函数.
在高速公路的情况中, 行为规划器将使用预测数据将自我车辆的状态设置为5个值中的一个, 并根据成本函数生成相应的车辆轨迹.
"KL"- Keep Lane"LCL"/"LCR"- Lane Change Left / Lane Change Right"PLCL"/"PLCR"- Prepare Lane Change Left / Prepare Lane Change Right
在实际情况下, 我们可以有多于以上的状态, 但至少有一个以上的有限状态总是好的.
典型的成本函数实例
但真实的成本函数不单单只有1/0两个选项, 在这我们提出两个成本函数.
场景是假设无人车位于左下角,目的地是右下角的G点,无人车前方有一个车辆,但是速度非常慢;
这时无人车的可选项有两个,一是keep lane直到终点,二是先变道左侧,超过前车,再变道回目的车道,快速行驶至目的地。
Intended_lane: 当前车道 + /-1, 如果车辆正在计划或执行车道变化, 否则为当前车道.
final_lane: 车辆最终到达的车道.
goal_lane:前方车辆所在的车道
distance_to_goal: 车辆到目标的距离.
Inefficiency_cost 成本函数考虑到当预定车道和最终车道的速度低于车辆的目标速度时, 成本会变得更高. 您可以使用车道速度函数来确定车道的速度.
double inefficiency_cost(int target_speed, int intended_lane, int final_lane,
const std::vector &lane_speeds) {
// Cost becomes higher for trajectories with intended lane and final lane
// that have traffic slower than target_speed.
double speed_intended = lane_speeds[intended_lane];
double speed_final = lane_speeds[final_lane];
double cost = (2.0*target_speed - speed_intended - speed_final)/target_speed;
return cost;
}
Goal_distance_cost 成本函数考虑到预定车道距离目标的距离和最终车道距离目标的距离增加都会导致成本增加. 当车辆接近目标时, 离开目标车道的成本也会增加.
double goal_distance_cost(int goal_lane, int intended_lane, int final_lane,
double distance_to_goal) {
// The cost increases with both the distance of intended lane from the goal
// and the distance of the final lane from the goal. The cost of being out
// of the goal lane also becomes larger as the vehicle approaches the goal.
int delta_d = 2.0 * goal_lane - intended_lane - final_lane;
double cost = 1 - exp(-(std::abs(delta_d) / distance_to_goal));
return cost;
}
最后将每个成本函数的输出值乘以对应的权重累积, 得到该轨迹最终的成本.
通过选择成本函数和权重, 以便在适当的时候驾驶在更快的车道.
轨迹成本排序(Trajectories cost ranking)
在这里我们将轨迹按成本函数排序, 将成本函数分解为若干子成本函数, 根据重要性的降低的次序, 相应地降低成本权重, 我们可以列出以下成本:
可行性成本(feasibility cost) : 关于避免碰撞和航行能力
安全成本(safety cost): 保持一定的缓冲距离, 良好的视野…
合法成本(legality cost): 遵守速度限制…
舒适成本(comfort cost): 最小化Jerk…
效率成本(efficiency cost): 关于速度和时间的目标…
在本项目中, 我们需要注意这些:
- 避免碰撞和安全距离: 通过检查预测和轨道之间的最小距离在一秒钟的时间范围内
- 能力成本: 提供了一个函数来检查每个候选轨迹的最大速度、加速度和Jerk
- 效率成本: 我们喜欢更高的目标速度(这是一个短期的速度)
- 车道成本: 我们通常喜欢呆在自己的车道上(假设其他成本相同) , 所以当相邻车道被其他车辆占据时, 我们施加惩罚(处罚是基于到自身车辆的距离). 我们优先考虑视野中没有车辆的车道.
所以这是一个相当保守的驾驶政策, 只有在目标车道有足够的自由空间时才变换车道.
作为进一步的发展, 长期车速能力应该与我们前面的车辆的速度(每条车道)相关联, 我们应该尝试选择能长时间保持速度的轨迹(不要突然加速又被迫减速,即有足够的free space).
作为一个总结, 在目前的实施情况下, 我们最终排序到9个候选轨迹, 并选择最符合我们的驾驶策略的一组加权成本函数定义.
轨迹生成器(Trajectory generation)
讨论轨迹成之前, 我们需要了解运动规划算法. 运动规划算法可以定义为在配置空间中最终的一系列可行的运动, 这些运动将驱动汽车从开始配置(由定位和传感器模块获得)移动到目标配置(由行为规划模块获得), 过程中会绕开障碍物(基于一些约束条件).
常见的运动规划算法有组合法, 位势场算法, 最优控制法和基于抽样的算法. 基于抽样的算法是我们今天讲解的重点. 基于抽样算法使用一个碰撞检测模块, 该模块探测自由空间, 测试是都一个配置在其中会发生碰撞. 抽样法不需要检测所有自由空间, 便可以发现一条路径. 搜索过的部分储存在一个图结构中, 然后我们可以使用图搜索算法进行搜索.
基于采样方法有两种, 一种是离散法, 另一种是概率统计法.
对于离散法, 常见的是A-star算法. A-star 算法是非结构化环境(停车场)中路径探索的最佳算法之一, 但是A-star 算法是离散的, 而机器人世界需要连续性. 因此我们基于运动学方程设计了混合A-Star, 从而使轨迹变得平滑.
对于结构化的环境如高速公路, 由于存在很多特定的规则和参考路径, A-star算法不再适合.
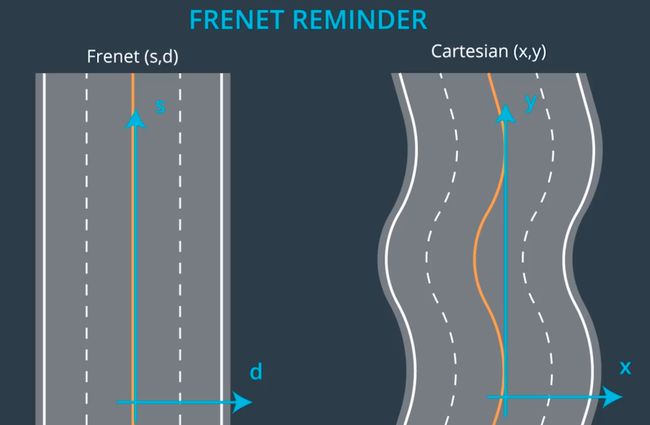
在讨论新的方法之前, 我们需要着重介绍Frenet坐标系.
由于道路的曲折, 导致在笛卡尔坐标系中计算轨迹的复杂度非常高. 为了解决这一问题, 我们以道路中心线作为参考线, D坐标代表横向运动, S代表纵向运动, 建立Frenet坐标系.
为了实现Jerk最小化(Jerk是指加速度的变化率, 如突然加速又突然减速会导致驾驶员极度不适), 轨迹可以通过两种不同的方式产生:
- 在(x, y)笛卡尔坐标中, 使用样条函数 (spline functions).
- 在(s, d) Frenet坐标系采用 Moritz Werling 提出的 Jerk 最小化轨迹方法.
第一种方法是在项目视频中提出的, 样调函数在给点若干点的前提下,拟合出尽量光滑的曲线, 该曲线保证通过所有点, 该方法简单易用,优于多项式拟合. 其中 s 和 d 坐标仅用于定义最终目标, 例如30米外的目标车道. 然后, 将这个目标点转换为(x, y)坐标, 并使用样条计算从起点到终点的轨迹(在笛卡尔坐标系中). 使用样条确保了生成的轨迹及其第一和第二导数的连续性: 因此我们保证了轨迹、速度和加速度的连续性, 包括终点和先前的弹道. 这种方法的优点是, 即使(s, d)估计不是那么精确, 它也能很好地工作, 因为它主要工作在(x, y)坐标系中, 而且大多数数学问题都是通过 c + + 样条库处理的, 使用起来非常简单. 就缺点而言, 它不能保证Jerk最小化, 这关系到使用者的舒适度.
样条曲线
这就是为什么在 Udacity 无人驾驶汽车纳米级讲座中, 提出了一种基于 Jerk 最小化轨迹的方法. 第二种方法在 Moritz Werling 的论文中有详细的描述, 我们在这里实现。
第二种方法的实现是在(s, d)坐标系下生成 JMT 轨迹. 出发点是试图找到一个最小的Jerk, 即用户最大的舒适性的轨迹. Jerk相当于加速度的变化, 因此我们需要研究第三个导数, 我们想要最小化从t_start到t_end所有第三个导数的总和, 如下面的链接所示, http://www.shadmehrlab.org/book/minimum_jerk/minimumjerk.htm , Jerk最小化轨迹必须是五次多项式.
因此, 我们最终寻找的是:
- 纵向部分的五次多项式: s (t)是5阶多项式
- 横向部分的五次多项式: d (t)是5阶多项式
注意, 在高速情况下, s (t)和 d (t)可以独立计算, 然后转换回(x, y)坐标, 而在低速情况下 s (t)和 d (t)不能独立计算(参见 Moritz Werling 关于这个主题的更多详细信息的论文). 这就是为什么在代码中有一个特殊情况, 在低速下, 我们只改变 s (t)并保持 d (t)不变. 尽管如此, 我们可以观察到在冷启动(刚运行代码)的情况下, JMT 轨迹产生不是那么好: 我们有无用的车轮运动. 这是一个值得进一步改进的主题(即使它没有违反任何速度, 加速度和挺举标准). 但是在冷启动之后, 一切都很好, 运行顺利.
现在的问题是找到这些 s (t)和 d (t)五次多项式. 我们剩下6个未知系数, 因此我们需要6个方程来解决这个问题. 利用函数及其一阶和二阶导数的起始条件和终止条件, 我们可以定义6个方程, 从而可以求出未知系数.
现在的关键点是正确地定义开始和结束条件.
对于起始条件, 除了使用先前生成的轨迹中的一个点之外, 没有其他选择. 为了确保位置、速度和加速度的连续性, 该点必须放置在先前生成的轨迹的某个地方, 而实际上车辆尚未到达这个位置. 在下面的实现中, 我们通常使用前面50个点(1秒)生成的轨迹中的第8个点(即8 * 20 ms). (设置第8个点考虑到模拟器的延迟和需要及时更新传感器融合信息, 而用50个点来计算一个轨道是为了避免碰撞检查)
在定义了开始条件之后, 我们必须定义适当的结束条件.
对于横向 d (t)轨迹, 它非常简单, 我们定义端点条件:
- df: 对应于目标车道的中心
- df_dot 和 df_ddot 设置为0, 因为在轨迹的结束点, 横向移动没有变化
对于纵向 s (t)轨迹, 我们定义为端点条件:
- sf_ddot = 0: 没有加速度
- sf_dot: 最终速度与我们的目标速度一致
- sf = si + sf_dot * T: 其中T设置为2秒, 因为我们不想变道花费太多的时间
现在我们已经明确了:
- Jerk 最小化轨迹是一个五次多项式(对于 s (t)和 d (t))
- 根据起始条件和终止条件, 可以定义了6个方程
- 轨迹的持续时间
- 有6个位置系数
从现在开始, 我们只需要解这些方程, 也就是做一个矩阵求逆来推导我们的6个未知系数.
这是JMT 多项式求解器的图表和公式:
最小化JMT轨迹系数求解代码:
vector Trajectory::JMT(vector< double> start, vector end, double T)
{
/*
Calculate the Jerk Minimizing Trajectory that connects the initial state
to the final state in time T.
INPUTS
start - the vehicles start location given as a length three array
corresponding to initial values of [s, s_dot, s_double_dot]
end - the desired end state for vehicle. Like "start" this is a
length three array.
T - The duration, in seconds, over which this maneuver should occur.
OUTPUT
an array of length 6, each value corresponding to a coefficent in the polynomial
s(t) = a_0 + a_1 * t + a_2 * t**2 + a_3 * t**3 + a_4 * t**4 + a_5 * t**5
EXAMPLE
> JMT( [0, 10, 0], [10, 10, 0], 1)
[0.0, 10.0, 0.0, 0.0, 0.0, 0.0]
*/
MatrixXd A(3,3);
VectorXd b(3);
VectorXd x(3);
A << pow(T,3), pow(T,4), pow(T,5),
3*pow(T,2), 4*pow(T,3), 5*pow(T,4),
6*T, 12*pow(T,2), 20*pow(T,3);
b << end[0] - (start[0] + start[1]*T + 0.5*start[2]*T*T),
end[1] - (start[1] + start[2]*T),
end[2] - start[2];
x = A.inverse() * b;
return {start[0], start[1], start[2]/2, x[0], x[1], x[2]};
}
至此我们完成了自动驾驶的路径规划任务。
基础项目代码管道(Udacity term3 simulator)
- 预测模块: term3 模拟器已经提供了自身车辆和其他车辆的速度,角度以及位置信息,我们需要首先确定车辆位于哪个车道以及其他车辆距离自身车辆的距离.
- 行为规划模块:基于安全合法舒适效率等原则设计成本函数,并计算自身车辆直行,左转,右转,减速等行为的成本。最终对不同行为的成本进行排序,从而确定目标点的位置,速度,和到达目标点的时间。
- 轨迹生成器:基于xy笛卡尔坐标系使用样条曲线生成从车辆的当前位置出发到目标位置的轨迹(xy路径点列表)。
具体细节可以参考项目github: https://github.com/williamhyin/CarND-Path-Planning
进阶项目代码管道(Udacity Bosch simulator)
- 地图模块: 使用样条库插值法为地图添加更多的参考路径点,从而提高地图参考路径的精度,以便于进行笛卡尔坐标系到Frenet坐标系的转化。
- 预测模块: Bosch 模拟器已经提供了自身车辆和其他车辆的速度,角度以及位置信息,我们需要首先确定车辆位于哪个车道以及其他车辆距离自身车辆的距离.
- 行为规划模块:基于安全合法舒适效率可行性等原则设计成本函数,并计算自身车辆直行-保持速度/加速/减速,左变道-保持速度/加速/减速,右变道保持速度/加速/减速等行为的成本。最终对不同行为的成本进行排序,从而确定目标点的位置,速度,和到达目标点的时间。
- 轨迹生成器:基于Frenet坐标系使用最小JMT轨迹算法生成从车辆的当前位置出发到目标位置的轨迹(s/d路径点列表)。
具体细节可以参考项目github:https://github.com/williamhyin/CarND-Path-Planning-Bosch
Backup:
# Example input
{
"timestamp" : 34512.21,
"vehicles" : [
{
"id" : 0,
"x" : -10.0,
"y" : 8.1,
"v_x" : 8.0,
"v_y" : 0.0,
"sigma_x" : 0.031,
"sigma_y" : 0.040,
"sigma_v_x" : 0.12,
"sigma_v_y" : 0.03,
},
{
"id" : 1,
"x" : 10.0,
"y" : 12.1,
"v_x" : -8.0,
"v_y" : 0.0,
"sigma_x" : 0.031,
"sigma_y" : 0.040,
"sigma_v_x" : 0.12,
"sigma_v_y" : 0.03,
},
]
}
# Example output
{
"timestamp" : 34512.21,
"vehicles" : [
{
"id" : 0,
"length": 3.4,
"width" : 1.5,
"predictions" : [
{
"probability" : 0.781,
"trajectory" : [
{
"x": -10.0,
"y": 8.1,
"yaw": 0.0,
"timestamp": 34512.71
},
{
"x": -6.0,
"y": 8.1,
"yaw": 0.0,
"timestamp": 34513.21
},
{
"x": -2.0,
"y": 8.1,
"yaw": 0.0,
"timestamp": 34513.71
},
{
"x": 2.0,
"y": 8.1,
"yaw": 0.0,
"timestamp": 34514.21
},
{
"x": 6.0,
"y": 8.1,
"yaw": 0.0,
"timestamp": 34514.71
},
{
"x": 10.0,
"y": 8.1,
"yaw": 0.0,
"timestamp": 34515.21
},
]
},
{
"probability" : 0.219,
"trajectory" : [
{
"x": -10.0,
"y": 8.1,
"yaw": 0.0,
"timestamp": 34512.71
},
{
"x": -7.0,
"y": 7.5,
"yaw": -5.2,
"timestamp": 34513.21
},
{
"x": -4.0,
"y": 6.1,
"yaw": -32.0,
"timestamp": 34513.71
},
{
"x": -3.0,
"y": 4.1,
"yaw": -73.2,
"timestamp": 34514.21
},
{
"x": -2.0,
"y": 1.2,
"yaw": -90.0,
"timestamp": 34514.71
},
{
"x": -2.0,
"y":-2.8,
"yaw": -90.0,
"timestamp": 34515.21
},
]
}
]
},
{
"id" : 1,
"length": 3.4,
"width" : 1.5,
"predictions" : [
{
"probability" : 1.0,
"trajectory" : [
{
"x": 10.0,
"y": 12.1,
"yaw": -180.0,
"timestamp": 34512.71
},
{
"x": 6.0,
"y": 12.1,
"yaw": -180.0,
"timestamp": 34513.21
},
{
"x": 2.0,
"y": 12.1,
"yaw": -180.0,
"timestamp": 34513.71
},
{
"x": -2.0,
"y": 12.1,
"yaw": -180.0,
"timestamp": 34514.21
},
{
"x": -6.0,
"y": 12.1,
"yaw": -180.0,
"timestamp": 34514.71
},
{
"x": -10.0,
"y": 12.1,
"yaw": -180.0,
"timestamp": 34515.21
}
]
}
]
}
]
}
引用:
- [Moritz Werling]: https://pdfs.semanticscholar.org/0e4c/282471fda509e8ec3edd555e32759fedf4d7.pdf "Optimal Trajectory Generation for Dynamic Street Scenarios in a Frenet Frame"
- [Udacity]: www.udacity.com
Linkedin: https://linkedin.com/in/williamhyin