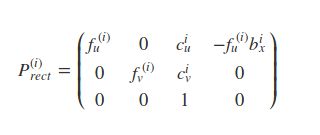自动驾驶视觉融合-相机标定与激光点云投影
Camera Calibration and LIDAR Cloud Projection
多传感器融合一直是自动驾驶领域非常火的名词, 但是如何融合不同传感器的原始数据, 很多人对此都没有清晰的思路. 本文的目标是在KITTI数据集上实现激光雷达和相机的数据融合. 然而激光雷达得到的是3D点云, 而单目相机得到的是2D图像, 如何将3D空间中的点投影到图像平面上, 从而获得激光雷达与图像平面相交的区域, 是本文研究的重点. 其次本文会介绍相机这个大家常见的传感器, 以及讲解如何对相机进行畸变校准.
Github: https://github.com/williamhyin/lidar_to_camera
Email: [email protected]
知乎专栏: 自动驾驶全栈工程师
Camera Technology
针孔相机与透镜
人类最早的相机是针孔相机. 通过在目标物体之间放置一个带有微小开口(针孔)的光栅可以设计一个非常简单的相机. 物体发出的光穿过针孔并落在感光表面上, 该感光表面将光信息存储为图像. 之所以将针孔做得如此之小, 是为了避免由于叠加来自感兴趣对象各个部分的光线而导致图像模糊.
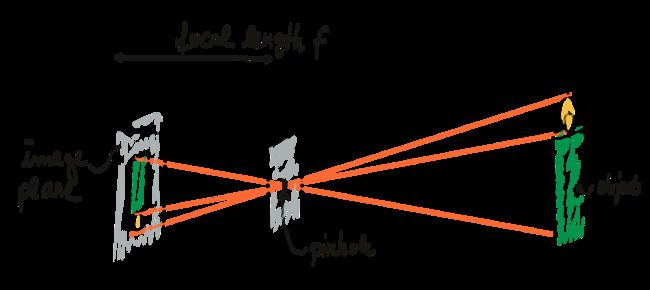
x ′ = f ⋅ x z y ′ = f ⋅ y z x^{\prime}=f \cdot \frac{x}{z} y^{\prime}=f \cdot \frac{y}{z} x′=f⋅zx y′=f⋅zy
基于上述方程, 只需要知道该物体在空间中的3D位置以及相机的焦距, 我们就可以计算出物体在图像平面上的2D位置. (请注意, 生成的坐标x’和y’是公制坐标(m), 而不是像素位置)
但是针孔相机存在透光量很小的问题, 而增大针孔又会导致成像模糊. 解决该问题的一种方法是使用透镜, 透镜能够捕获从感兴趣对象的同一点发出的多束光线. 因此现代相机几乎都使用透镜.
一般情况尺寸适当且位置合适的镜头可折射从空间中的物体上的点P1发出的所有光线, 使它们会聚到在图像平面中单个点p1’. 穿过镜头中心的光线不会发生折射, 它们会一直沿直线直到与像平面相交.
而物体上较近或较远的点却不会聚在图像平面上, 因为它们发出的光线不是会聚在一个点上, 而是会聚在一个半径有限的圆上. 这种模糊的圈子通常称为 circle of confusion (COF). 为了减少模糊, 可以使用光圈, 该光圈是通常可调大小的同心开口, 直接位于镜头后面. 下图说明了原理:

通过减小光圈的直径, 可以阻挡通过外边缘镜头的光线, 从而减小了像平面上COF的大小. 从上图中可以看使用较小的光圈可减少模糊, 但以降低光敏度为代价. 光圈越大, 越多的光线聚焦在图像区域上, 从而使图像更明亮, 信噪比更好.
像平面坐标系到像素坐标系的转换
3D空间中的点在图像平面上的投影与我们在实际的数字图像中看到的并不直接对应, 实际的数字图像由数千个图片像素组成. 因此我们需要实现从图像平面到数字图像上的投影.
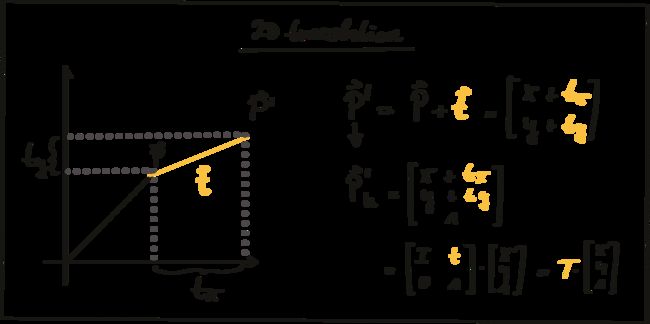
在下图中相机中心是O点, 伴随着坐标系i,j,k. 其中k指向图像平面. 与k轴位置相交的C点被称为主点, 代表着图像平面的中心. 以主点为原点的右手平面坐标系o-xy为像平面坐标系.
因此, 在空间上将点P投影到图像平面上之后的第一步是减去主点坐标, 以使离散图像具有其自身的坐标系, 例如该坐标系的中心为图像平面的左下角.
转换过程的第二步是从公制坐标(m)转换为像素坐标. 为此, 我们可以使用校准程序提供的参数k和l, 这些参数将将米转换为像素, 并且可以轻松地将其集成到投影方程式中, 如下所示. 请注意, 在像素坐标系中, y轴的原点位于左上角, 并指向下方.
P ⃗ → P ⃗ ′ ( x , y , z ) ⊤ → ( f ⋅ k ⋅ x 2 + c x , f ⋅ l ⋅ y z + c y ) ⊤ [ k , l ] = p i x e l / m \begin{aligned} &\vec{P} \rightarrow \vec{P}^{\prime}\\ &(x, y, z)^{\top} \rightarrow\left(f \cdot k \cdot \frac{x}{2}+c_{x}, f \cdot l \cdot \frac{y}{z}+c_{y}\right)^{\top}\\ &[k, l]=pixel / m \end{aligned} P→P′(x,y,z)⊤→(f⋅k⋅2x+cx,f⋅l⋅zy+cy)⊤[k,l]=pixel/m
fk一般在转换矩阵中称为alpha, fl称为beta.
相机校准(camera calibration)
使用镜头虽然可以像针孔相机一样计算空间中的3D点通过镜头后在图像平面上的2D位置, 但是大部分镜头会将失真引入图像. 最常见的是变形称为“radial distortion”, 这是由于镜头的焦距在其直径上不一致. 一般情况镜头的放大效果根据相机中心(光轴)和通过镜头的光线之间的距离而变化. 如果放大倍数增加, 则产生的失真效果称为“pin cushion distortion”. 如果减小, 则称为“barrel distortion”. 使用广角镜如GOPRO时, 通常会发生” Barrel distortions“.
请记住, 如果我们需要通过图像得出关于目标物体(例如车辆)的空间位置, 一定要对相机进行畸变校准(calibration). 通常, 这是通过拍摄一组平面棋盘图案的图片来完成的, 可以从这些对象的已知几何形状中可靠地导出所有镜头和图像传感器参数. 消除相机图像失真的过程称为校正(rectification).
网上有很多关于如何使用OPENCV对相机进行畸变校准的教程, 我给大家推荐OPENCV官方的教程PYTHON, C++.
但是我最建议的方式是通过MATLAB的神器tools Camera Calibrator来进行畸变校准, 非常的高效和迅速, 不需要自己编码, 而且能直观的看到校正前后的图像变化. 这是MATLAB的校准教程.
请注意得到相机内参和畸变参数的过程是畸变校准(calibration), 拿着相机内参和畸变参数去消除相机图像失真的才叫校正(rectification). 下文的KITTI数据集已经给出了相机内参和畸变参数, 因此不需要再去拍棋牌图校准了.
在得到相机内参和畸变参数后可以通过OPENCV函数直接对图像进行校正, 你不需要了解复杂的公式.
畸变参数:注意有的文章中还会出现k4,k5,k6, 这三个参数基本用不到, 可以忽略.
Distortion coefficients = ( k 1 k 2 p 1 p 2 k 3 ) \text { Distortion coefficients }=\left(\mathrm{k}_{1} \mathrm{k}_{2} \mathrm{p}_{1} \mathrm{p}_{2} \mathrm{k}_{3}\right) Distortion coefficients =(k1k2p1p2k3)
基于PYTHON OPENCV 的畸变校准和校正可以遵循如下步骤:
// Converting an image, imported by cv2 or the glob API, to grayscale:
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
// ret, corners = cv2.findChessboardCorners(gray, (8,6), None)
ret, corners = cv2.findChessboardCorners(gray, (8,6), None)
// Drawing detected corners on an image:
img = cv2.drawChessboardCorners(img, (8,6), corners, ret)
// Camera calibration, given object points, image points, and the shape of the grayscale image
ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(objpoints, imgpoints, gray.shape[::-1], None, None)
// Undistorting a test image
dst = cv2.undistort(img, mtx, dist, None, mtx)
而c++代码相对复杂, 在实际校正这一块, 首先调用 cv: : initundistortcorrectfymap 来查找转换矩阵, 然后使用 cv: : : remap 函数执行转换. 详情看上文中的教程链接.
CMOS 相机
CMOS (Complementary Metal-oxide Semiconductor)技术具有几个优点:与CCD(Charge-Coupled Device)不同, CMOS芯片集成了放大器和A / D转换器, 这带来了巨大的成本优势. 对于CCD, 这些组件位于芯片外部. CMOS传感器还具有更快的数据读取速度, 更低的功耗, 更高的抗噪能力以及更小的系统尺寸. 由于这些优点, 在汽车应用中, 几乎所有相机都使用CMOS传感器.
值得注意的是对于自动驾驶汽车的相机, 分辨率实际上并不是那么重要, 目前大部分汽车相机像素在1百万到8百万像素这个区间内, 相对于手机动辄1亿的像素小的不能再小了. 对于汽车相机重要的是感光度, 因为像素量越小, 像素面积越大, 意味着更多的光子落入一个像素, 具有更好的弱光可见性.
LIDAR Cloud Projection
齐次坐标系
在开始激光点云投影前, 首先我们得讨论什么是齐次坐标. 齐次坐标是指一个用于投影几何里的坐标系统, 如同欧几里得坐标系一样. 那我们为什么需要齐次坐标呢?欧几里得坐标系不是很好吗?
上文提过, 在相机世界中, 3D外界点转换到2D图像像素点转换方程是
p ⃗ = [ x y z ] → p ⃗ ′ = [ α x z + c x β y z + c y ] \vec{p}=\left[\begin{array}{l} x \\ y \\ z \end{array}\right] \rightarrow \vec{p}^{\prime}=\left[\begin{array}{c} \alpha \frac{x}{z}+c_{x} \\ \beta \frac{y}{z}+c_{y} \end{array}\right] p=⎣⎡xyz⎦⎤→p′=[αzx+cxβzy+cy]
我们可以通过相机的内在参数 intrinsic camera parameters 实现这一转换. 但是激光雷达的外部坐标系和相机的外部坐标系位置是不一样的. 因此除了构成投影几何形状的固有相机内参数外, 我们还需要有关相机和激光雷达在公共参考坐标系中的位置和对齐方式的其他信息. 几乎每一家自动驾驶厂商的激光雷达和相机的放置位置都是不一样的, 这些信息往往只能厂商给出.
从激光雷达的位置移动到相机的位置涉及平移和旋转操作, 我们需要将其应用于每个3D点. 问题在于我们得到的投影方程的问题是涉及到 z 的除法, 这使得它们是非线性的(3维), 从而使我们无法将它们转化为更方便的矩阵向量形式.
避免此问题的一种方法是同时更改激光雷达和相机的坐标系, 从原始的欧几里得坐标系转换为齐次坐标系的形式. 在两个欧几里得坐标系之间来回移动是一种非线性操作, 但是一旦我们处于齐次坐标系中, 投影变换将变为线性, 因此可以表示为简单的矩阵向量乘法. 两个坐标系之间的转换如下图所示.
欧几里得坐标->齐次坐标
( x , y ) → [ x y 1 ] ( x , y , z ) → [ x y z 1 ] (x, y) \rightarrow\left[\begin{array}{l} x \\ y \\ 1 \end{array}\right] \quad(x, y, z) \rightarrow\left[\begin{array}{l} x\\ y\\ z\\ 1 \end{array}\right] (x,y)→⎣⎡xy1⎦⎤(x,y,z)→⎣⎢⎢⎡xyz1⎦⎥⎥⎤
n维欧氏坐标系中的一个点由具有n个分量的向量表示. 通过简单地将数字1添加为附加分量, 可以实现到(n+1)维同构坐标的转换. 该变换可以应用于图像坐标(左侧)以及场景坐标(右侧).
// 1. Convert current Lidar point into homogeneous coordinates and store it in the 4D variable X.
X.at(0, 0) = it->x;
X.at(1, 0) = it->y;
X.at(2, 0) = it->z;
X.at(3, 0) = 1;
齐次坐标->欧几里得坐标
[ x y w ] → ( x / w , y / w ) [ x y z w ] → ( x / w , y / w , z / w ) \left[\begin{array}{l} x \\ y \\ w \end{array}\right] \rightarrow\left(x/w, y/ w\right) \quad\left[\begin{array}{l} x \\ y \\ z \\ w \end{array}\right] \rightarrow\left(x/w, y/w, z/w\right) ⎣⎡xyw⎦⎤→(x/w,y/w)⎣⎢⎢⎡xyzw⎦⎥⎥⎤→(x/w,y/w,z/w)
从齐次坐标转换回欧几里得坐标系, 只需要通过删除最后一个坐标并将前n个坐标除以第(n + 1)个坐标.
cv::Point pt;
pt.x = Y.at(0, 0) / Y.at(0, 2);
pt.y = Y.at(1, 0) / Y.at(0, 2);
内参矩阵
有了齐次坐标系的帮助, 我们可以用矩阵向量的形式表示投影方程了:
P ⃗ h ′ = [ α ⋅ x + c x ⋅ z β ⋅ y + c y ⋅ z z ] = [ α 0 c x 0 0 β c y 0 0 0 1 0 ] ⋅ [ x y z 1 ] \vec{P}_{h}^{\prime}=\left[\begin{array}{c} \alpha \cdot x+c_{x} \cdot z \\ \beta \cdot y+c_{y} \cdot z \\ z \end{array}\right]=\left[\begin{array}{cccc} \alpha & 0 & c_{x} & 0 \\ 0 & \beta & c_{y} & 0 \\ 0 & 0 & 1 & 0 \end{array}\right] \cdot\left[\begin{array}{l} x \\ y \\ z \\ 1 \end{array}\right] Ph′=⎣⎡α⋅x+cx⋅zβ⋅y+cy⋅zz⎦⎤=⎣⎡α000β0cxcy1000⎦⎤⋅⎣⎢⎢⎡xyz1⎦⎥⎥⎤
上述方程从左到右依次是齐次坐标系的相机投影几何转换矩阵/ 相机内参数矩阵K/ 齐次坐标点
相机内参数以矩阵形式排列, 可以方便地以紧凑的方式表示针孔相机模型的属性.
内参矩阵告诉你在外部世界的点在经过外参矩阵变换之后, 是如何继续经过摄像机的镜头、并通过针孔成像和电子转化而成为像素点的.
外参矩阵
现在我们已经实现了在相机坐标系中3D空间中的点P到2D像素平面中的点P’之间的映射.
但是激光雷达和相机的坐标系所在空间位置是不一样的, 它们都需要在车辆坐标系中进行校准.
如下是常见的车辆坐标系
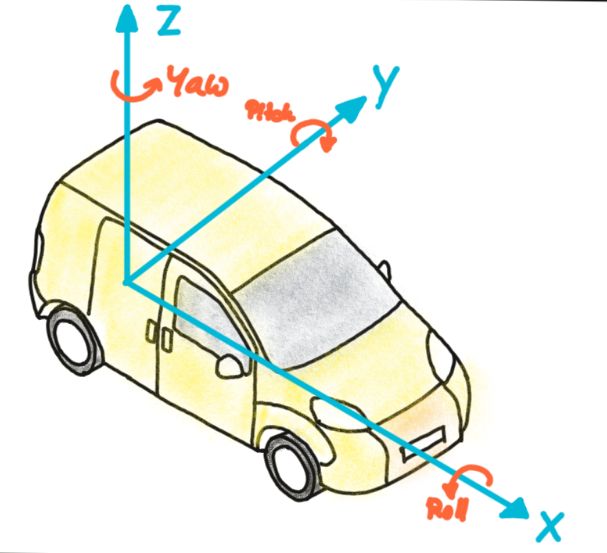
车辆坐标系的原点放置在后轴中点下方的地面上, x轴指向行驶方向.
为了将在激光雷达传感器坐标系中测量的点投影到相机中, 我们需要在投影操作中添加其他转换, 以使我们能够将车辆坐标系中的点关联到相机坐标系, 反之亦然. 通常, 这种投影操作可以分为三个部分:平移, 旋转和缩放. 让我们依次看一下它们:
平移(translation):
通过添加平移向量t到P, 使得P点线性平移到新位置P’.
在齐次坐标中, 我们可以使用大小为N的单位矩阵I连接平移向量t表示.
p ⃗ h ′ → [ I t 0 1 ] ⋅ [ x y ] \vec{p}_{h}^{\prime}\rightarrow\left[\begin{array}{ll} I & t \\ 0 & 1 \end{array}\right] \cdot\left[\begin{array}{l} x \\ y \end{array}\right] ph′→[I0t1]⋅[xy]
缩放(scale):
通过成分乘以尺度向量s实现缩放.
p ⃗ h ′ → [ s x x s y , y 1 ] = [ s x 0 0 0 s y 0 0 0 1 ] [ x y 1 ] = s ⋅ [ x y 1 ] \vec{p}_{h}^{\prime} \rightarrow\left[\begin{array}{c} s_{x} x \\ s_{y}, y \\ 1 \end{array}\right]=\left[\begin{array}{ccc} s_{x} & 0 & 0 \\ 0 & s_{y} & 0 \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{l} x \\ y \\ 1 \end{array}\right]=s \cdot\left[\begin{array}{c} x \\ y \\ 1 \end{array}\right] ph′→⎣⎡sxxsy,y1⎦⎤=⎣⎡sx000sy0001⎦⎤⎣⎡xy1⎦⎤=s⋅⎣⎡xy1⎦⎤
旋转(rotation):
下图为点P在顺时针方向上的旋转的实现:
其中R被称为旋转矩阵. 在3D空间中, 点P的旋转是围绕x,y,z三个轴实现的, 因此可以表述为下面的旋转公式.
R x = [ 1 0 0 0 cos ϕ x − sin ϕ x 0 sin ϕ x cos ϕ x ] R y = [ cos θ y 0 sin θ y 0 1 0 − sin θ y 0 cos θ y ] R z = [ cos θ z − sin θ z 0 sin θ 2 cos θ z 0 0 0 1 ] \begin{aligned} &R_{x}=\left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & \cos \phi_{x} & -\sin \phi_{x} \\ 0 & \sin \phi_{x} & \cos \phi_{x} \end{array}\right]\\ &R_{y}=\left[\begin{array}{ccc} \cos \theta_{y} & 0 & \sin \theta_{y} \\ 0 & 1 & 0 \\ -\sin \theta_{y} & 0 & \cos \theta_{y} \end{array}\right]\\ &R_{z}=\left[\begin{array}{ccc} \cos \theta_{z} & -\sin \theta_{z} & 0 \\ \sin \theta_{2} & \cos \theta_{z} & 0 \\ 0 & 0 & 1 \end{array}\right] \end{aligned} Rx=⎣⎡1000cosϕxsinϕx0−sinϕxcosϕx⎦⎤Ry=⎣⎡cosθy0−sinθy010sinθy0cosθy⎦⎤Rz=⎣⎡cosθzsinθ20−sinθzcosθz0001⎦⎤
合在一起就是3D旋转公式:
R = R z ⋅ R y ⋅ R x R=R_{z} \cdot R_{y} \cdot R_{x} R=Rz⋅Ry⋅Rx
齐次坐标的优点之一是, 它们可以通过级联几个矩阵-矢量乘法来轻松组合多个变换.
平移矩阵T和旋转矩阵R一起被称为外参矩阵. 它们共同描述了如何把点从世界坐标系转换到相机坐标系. 需要注意的是缩放成分S已集成到内矩阵中K, 因此不再是外参矩阵的一部分.
3D 投影方程
通过将各个外参矩阵和内参矩阵进行级联, 实现了3D激光雷达到2D图像平面上的投影.
实现3D投影需要从完成这些坐标系的变换:
激光雷达世界坐标系->相机坐标系(激光雷达和相机都在车辆坐标系中进行位置校准, 从而互相关联)->像平面坐标系->像素坐标系.欧几里得坐标系->齐次坐标系->欧几里得坐标系.
相机投影玩具
在这里给对计算机视觉成像缺乏一定想象的朋友们提供一个很好玩的图像投影工具Perspective Camera Toy. 这个工具由Ksimek开发. 你可以在里面随意调节相机内参外参, 直观的感受这些参数对于最终成像的影响.
KITTI 传感器配置
接下来我们会使用KITTI的自动驾驶数据集来实现3D空间中的激光雷达点(激光雷达外部坐标系)到相机2D图像平面的投影(像素坐标系).
首先我初步介绍下KITTI的传感器的布置.
如上图所示这辆帕萨特配备了两个前置灰度摄像头和两个彩色摄像头, 一个安装在车顶上的Velodyne Lidar以及一个惯性测量单元或IMU. 现在KIT MRT所的最新的自动驾驶车辆是奥迪Q7, 传感器布置基本相似.
我们可以从KITTI的网站下载对应数据包的带有内参和外参的校准文件calib.zip.
calib.zip校准文件夹中包括三个子文件:calib_velo_to_cam.txt, calib_imu_to_velo.txt和calib_cam_to_cam.txt. calib_velo_to_cam.txt中的内容与Velodyne激光雷达和左灰色相机(编号为0)有关.
calib_time: 15-Mar-2012 11:37:16
R: 7.533745e-03 -9.999714e-01 -6.166020e-04 1.480249e-02 7.280733e-04 -9.998902e-01 9.998621e-01 7.523790e-03 1.480755e-02
T: -4.069766e-03 -7.631618e-02 -2.717806e-01
其中矩阵R和T为我们提供了传感器设置的外参数.
- R:3x3旋转矩阵
- T:3x1平移向量
为了执行到图像像素平面的投影, 我们还需要有关内参数的信息, 它们储存在calib_cam_to_cam.txt中.
calib_time: 09-Jan-2012 13:57:47
corner_dist: 9.950000e-02
S_00: 1.392000e+03 5.120000e+02
K_00: 9.842439e+02 0.000000e+00 6.900000e+02 0.000000e+00 9.808141e+02 2.331966e+02 0.000000e+00 0.000000e+00 1.000000e+00
D_00: -3.728755e-01 2.037299e-01 2.219027e-03 1.383707e-03 -7.233722e-02
R_00: 1.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 1.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 1.000000e+00
T_00: 2.573699e-16 -1.059758e-16 1.614870e-16
S_rect_00: 1.242000e+03 3.750000e+02
R_rect_00: 9.999239e-01 9.837760e-03 -7.445048e-03 -9.869795e-03 9.999421e-01 -4.278459e-03 7.402527e-03 4.351614e-03 9.999631e-01
P_rect_00: 7.215377e+02 0.000000e+00 6.095593e+02 0.000000e+00 0.000000e+00 7.215377e+02 1.728540e+02 0.000000e+00 0.000000e+00 0.000000e+00 1.000000e+00 0.000000e+00
....
....
S_03: 1.392000e+03 5.120000e+02
K_03: 9.037596e+02 0.000000e+00 6.957519e+02 0.000000e+00 9.019653e+02 2.242509e+02 0.000000e+00 0.000000e+00 1.000000e+00
D_03: -3.639558e-01 1.788651e-01 6.029694e-04 -3.922424e-04 -5.382460e-02
R_03: 9.995599e-01 1.699522e-02 -2.431313e-02 -1.704422e-02 9.998531e-01 -1.809756e-03 2.427880e-02 2.223358e-03 9.997028e-01
T_03: -4.731050e-01 5.551470e-03 -5.250882e-03
S_rect_03: 1.242000e+03 3.750000e+02
R_rect_03: 9.998321e-01 -7.193136e-03 1.685599e-02 7.232804e-03 9.999712e-01 -2.293585e-03 -1.683901e-02 2.415116e-03 9.998553e-01
P_rect_03: 7.215377e+02 0.000000e+00 6.095593e+02 -3.395242e+02 0.000000e+00 7.215377e+02 1.728540e+02 2.199936e+00 0.000000e+00 0.000000e+00 1.000000e+00 2.729905e-03
其中00,01,02,03 代表相机的编号, 0表示左边灰度相机, 1右边灰度相机, 2左边彩色相机, 3右边彩色相机.
-
S_xx:1x2 矫正前的图像xx的大小
-
K_xx:3x3 矫正前相机xx的校准矩阵
-
D_xx:1x5 矫正前相机xx的失真向量
- 形式是
[k1, k2, p1, p2, k3]. k1, k2 和k3 是径向畸变系数, 而p1 和p2 是切向畸变系数.
- 形式是
-
R_xx:3x3 (外部)的旋转矩阵(从相机0到相机xx)
-
T_xx:3x1 (外部)的平移矢量(从相机0到相机xx)
-
S_rect_xx:1x2 矫正后的图像xx的大小
-
R_rect_xx:3x3 纠正旋转矩阵(使图像平面共面)
- 即以立体方式对齐两个立体相机的摄像头(KITTI车辆中有两个Point Grey摄像头)
-
P_rect_xx:3x4 矫正后的投影矩阵, 包含上述的相机内参矩阵K.
fu/fv 为相机焦距, 一般相同, cu/cv为主点坐标(相对于成像平面), s为坐标轴倾斜参数, 理想情况下为0. b(i) 代表其他相机相对于cam 0的偏移. 在从相机0投影到其他相机时需要.
以下等式说明了如何使用齐次坐标在相机0的图像平面上将空间中的3D激光雷达点X投影到2D像素点Y(使用Kitti自述文件中的表示法):
Y = P − r e c t − x x ∗ R − r e c t − 00 ∗ ( R ∣ T ) − v e l o − t o − c a m ∗ x Y=P_{-} r e c t_{-} x x * R_{-} r e c t_{-} 00 *(R | T)_{-} v e l o_{-} t o_{-} c a m * x Y=P−rect−xx∗R−rect−00∗(R∣T)−velo−to−cam∗x
RT_velo_to_cam * x :是将Velodyne坐标中的点x投影到编号为0的相机(参考相机)坐标系中
R_rect00 *RT_velo_to_cam * x :是将Velodyne坐标中的点x投影到编号为0的相机(参考相机)坐标系中, 再以参考相机0为基础进行图像共面对齐修正(这是使用KITTI数据集的进行3D投影的必要操作)
P_rect_00 * R_rect00 *RT_velo_to_cam * x :是将Velodyne坐标中的点x投影到编号为0的相机(参考相机)坐标系中, 再进行图像共面对齐修正, 然后投影到相机0的像素坐标系中. 如果将P_rect_00改成P_rect_2, 也就是从参考相机0投影到相机2的像素坐标系中(其他相机相对与相机0有偏移b(i)).
以下为实现激光雷达3D点云投影到2D图像平面的步骤:
// 1. Convert current Lidar point into homogeneous coordinates and store it in the 4D variable X.
X.at(0, 0) = it->x;
X.at(1, 0) = it->y;
X.at(2, 0) = it->z;
X.at(3, 0) = 1;
// 2. Then, apply the projection equation as detailed in lesson 5.1 to map X onto the image plane of the camera.
// Store the result in Y.
Y = P_rect_00 * R_rect_00 * RT * X;
// 3. Once this is done, transform Y back into Euclidean coordinates and store the result in the variable pt.
cv::Point pt;
pt.x = Y.at(0, 0) / Y.at(0, 2);
pt.y = Y.at(1, 0) / Y.at(0, 2);
在完成欧几里得坐标转齐次坐标, 转换函数, 齐次坐标转欧几里得坐标这三步之后我们完成了激光雷达到相机的点投影, 从而获得了激光雷达与图像平面相交的区域.
引用:
- UDACITY
如果有什么疑问,可以随时联系我的个人邮箱。
如果你觉得我的文章对你有帮助,请帮忙点个赞~\(≧▽≦)/~
Linkedin: https://linkedin.com/in/williamhyin