自动驾驶感知融合-卡尔曼及扩展卡尔曼滤波(Lidar&Radar)

Kalman Filter and Extended Kalman Filter

卡尔曼滤波是自动驾驶领域最常用的数据最优估计算法。人们对它的第一印象往往是它那复杂的线性代数表达式。本文将介绍卡尔曼滤波及其变种扩展卡尔曼滤波的数学原理及代码实现，帮助初学者熟悉和掌握卡尔曼滤波。在实际项目中我们会融合激光雷达和毫米波雷达的测量数据，从而精确地追踪目标的位置和速度。

Github: https://github.com/williamhyin/CarND-Extended-Kalman-Filter

Email: [email protected]

知乎专栏: 自动驾驶全栈工程师

Kalman Filter

1. 首先我们需要了解什么是卡尔曼滤波？

根据维基百科的官方解释，卡尔曼滤波(Kalman Filter)使用随时间推移观察到的一系列测量值（包含统计噪声和其他误差），生成未知变量的估计值，该估计值往往更多通过估计每个时间范围内变量的联合概率分布，结果因此比仅基于单个测量的结果更准确。

听起来稍微有点复杂，也就是说，卡尔曼滤波器是一种最优估计算法，它能够从一系列的不完全及包含噪声的测量中，估计动态系统的状态。

2. 其次我们要了解为什么需要卡尔曼滤波?

使用卡尔曼滤波的根本原因其实是来自传感器的测量结果不是100％可靠，如果毫无误差，或者误差远低于期望阈值，则完全不需要卡尔曼滤波，直接使用测量数据更新下一个状态即可。

在自动驾驶领域，卡尔曼滤波器广泛被用于通过特征级融合激光雷达和毫米波雷达的数据，估计汽车的位置和速度。 不同的传感器提取得到的测量结果如距离，速度，角度，因为受到信号漂移或噪声的影响，往是不准确的。而卡尔曼滤波为我们提供了一种将来自不同传感器的测量结果与预测位置的数学模型相结合的方法。它根据我们对一个特定传感器或模型的信任程度，来更新测量值和预估值之间的可信权重，从而获得对准确位置的最佳估计。

3. 卡尔曼滤波的步骤？

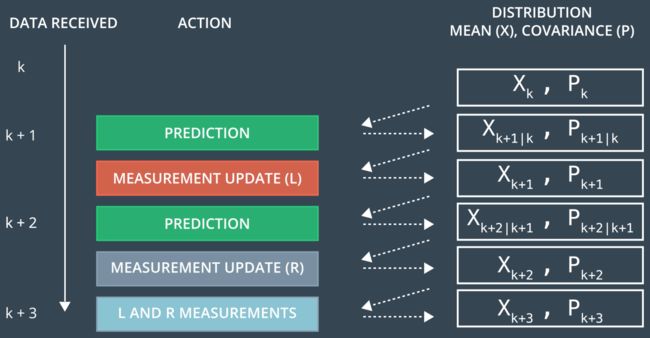
卡尔曼滤波器的操作包括两个阶段：预测与更新。在预测阶段，滤波器使用上一状态的估计结果，做出对当前状态的估计。在更新阶段，滤波器利用当前状态的观测值优化在预测阶段获得的预估值，以获得一个当前阶段更精确的新估计值。

每当我们从传感器获取新数据时，我们都会重复这两个步骤，不断更新位置状态估计值和误差协方差矩阵P的准确性。

值得注意的是测量更新基于的依据是贝叶斯法则。当我们有了上一时刻的状态向量的先验概率P(x), 又有了测量值的似然P(z|x)，似然是指在当前位置下，我们能得到的测量值
，在P(z)为一个常数的情况下，我们求目标位置的概率分布其实就是在求后验概率P(x|z)。
$$P(\mathbf{x}|\mathbf{z})=\frac{P(\mathbf{z}|\mathbf{x})P(\mathbf{x})}{P(\mathbf{z})}$$
而预测更新是基于全概率公式。
$$P(B)=\sum _{i=1}^{n}P\left(A_i\right)P\left(B|A_i\right)$$

在下面的例子中，我们可以用在概率密度函数的帮助下解释卡尔曼滤波的工作原理。

在最初的时间步骤 k-1，目标的位置是平均位置为 x_k-1的高斯分布。 之后基于运动模型进行预测，得到时刻 k 的 目标位置x_k ，由于预测本身具有较大的不确定性，因此预测的位置结果具有较大的方差。与此同时我们获得来自传感器的测量结果 y ，测量值的不确定性较小，因此测量的位置结果具有较小的方差。卡尔曼滤波器通过将预测和测量两个概率函数相乘，来估计最佳位置。值得注意的是通过数学推导可以发现相乘的结果是一个分布紧密具有更小方差的高斯函数，意味着最终位置估计准确性得到了提高。

4. 卡尔曼滤波与隐马尔科夫模型的关系？

卡尔曼滤波建立在线性代数和隐马尔可夫模型（hidden Markov model）上。其基本动态系统可以用一个马尔可夫链表示。它是是一种递归的估计，即只要获知上一时刻状态的估计值以及当前状态的观测值就可以计算出当前状态的估计值，因此不需要记录观测或者估计的历史信息。

卡尔曼向量与矩阵

卡尔曼滤波器的在预测和测量步骤中相互传递的数值有以下两个：

• $$\hat{\mathbf{x}}:状态的估计$$

• $$\mathbf{P}：状态误差协方差矩阵，度量估计值的精确程度。$$

以下是维基百科中对于卡尔曼滤波各个向量与矩阵的数学描述，初看非常复杂，但其实熟悉之后就会发现，你只需要套公式。我会在后续章节中，详细讲解各个向量和矩阵的意义。在下文中Xk-1|k-1用x表示，Xk|k用x’ 表示，其他变量相似的表示有同样的含义。

预测

假设我们知道一个物体的当前位置和速度，我们把它保持在 x 变量中。 现在一秒钟已经过去了。因为我们一秒钟前就知道了物体的位置和速度，以及匀加速运动的加速度 a，那么我们可以在一秒钟后预测物体的位置。如果我们假设物体以同样的速度运动，则我们可以用等式计算预测值。

但也许物体并没有保持完全相同的速度。 也许物体改变了方向，加速或减速。 所以当我们一秒钟后预测位置时，我们的不确定性就增加了。

代表不确定性增加了。

我们来分别讨论各个变量的含义：

• x是平均状态向量，包含被t-1时刻被跟踪对象综合预测和测量得到的估计值，该估计值包括四个值：(px, py, vx, vy)，均基于笛卡尔坐标。x之所以被称为“mean state vector”，是因为位置和速度由均值为x的高斯分布表示。

• F是预测下一个状态值的状态变换矩阵，为此我们需要一个现实中的线性运动模型。

$$\{\begin{array}{l}{p}_x^{\prime }=p_x+v_x\Delta t+\frac{a_x\Delta t^2}{2}\\ p_y^{\prime }=p_y+v_y\Delta t+\frac{a_y\Delta t^2}{2}\\ v_x^{\prime }=v_x+a_x\Delta t\\ v_y^{\prime }=v_y+a_y\Delta t\end{array}$$

根据上述线性速度模型，我们得到下列状态转移方程：
$$\begin{gathered} \left(\begin{array}{c}{p}_x^{\prime }\\ p_y^{\prime }\\ v_x^{\prime }\\ v_y^{\prime }\end{array}\right)=\left(\begin{array}{cccc}1& 0& \Delta t& 0\\ 0& 1& 0& \Delta t\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right)\left(\begin{array}{c}{p}_x\\ p_y\\ v_x\\ v_y\end{array}\right)+\left(\begin{array}{c}\frac{\Delta t^2}{2}\\ \frac{\Delta t^2}{2}\\ \Delta t\\ \Delta t\end{array}\right)\left(\begin{array}{c}{a}_x\\ a_y\\ a_x\\ a_y\end{array}\right) \\ {x}^{\prime }=Fx+Bu+w \end{gathered}$$
这里F是状态变换矩阵，x‘ 是基于t-1时刻估计状态x下理论预测的t时刻的状态，B被称为控制矩阵，u被称为控制变量，由于汽车的运动并不严格遵循匀加速运动，因此需要在等式后面加上w噪声项。
$$x^{\prime }=Fx+\nu$$
但是在本项目的表达式中我们省略了Bu，原因是Bu代表加速度对于位置更新的影响，而在本项目采用恒速模型，我们无法测量或知道被跟踪物体的确切加速度，因此我们设置Bu=0，将加速度的影响加入到w噪声项中，用v表示它们。

可以看到，这个等式其实就是 x'= F * x +noise。这个噪声被称为过程噪声，也被叫做运动噪声。过程噪声是表示预测位置时，物体位置的不确定性。由于我们采用恒速模型，因此我们可以在状态预测代码中彻底忽略这个噪声，将这个噪声的影响放入过程协方差矩阵Q中，用来描述状态预测的不确定性，也就是说对于恒速模型的代码x'= F * x。

• Q是过程协方差矩阵，它是与过程噪声相关的协方差矩阵。

对于过程协方差矩阵的计算稍微复杂些，下面我会为大家推导：

在上文中说道我们的状态矢量x只跟踪位置和速度，由于加速度是未知的，我们将加速度建模为一个随机噪声。

这种随机噪声可以用上面导出的方程中的最后一项解析地表示出来。 v 过程噪声，可以理解为随机加速度噪声矢量:
$$\nu =\left(\begin{array}{c}{\nu }_{px}\\ {\nu }_{py}\\ {\nu }_{vx}\\ {\nu }_{vy}\end{array}\right)=\left(\begin{array}{c}\frac{a_x\Delta t^2}{2}\\ \frac{a_y\Delta t^2}{2}\\ a_x\Delta t\\ a_y\Delta t\end{array}\right)$$
这个矢量可以用均值为0，协方差为Q的二元独立高斯分布表示，即ν∼N (0,Q).

我们可以将v继续分解
$$\nu =\left(\begin{array}{c}\frac{a_z\Delta t^2}{2}\\ \frac{a_y\Delta t^2}{2}\\ a_x\Delta t\\ a_y\Delta t\end{array}\right)=\left(\begin{array}{cc}\frac{\Delta t^2}{2}& 0\\ 0& \frac{\Delta t^2}{2}\\ \Delta t& 0\\ 0& \Delta t\end{array}\right)\left(\begin{array}{l}{a}_x\\ a_y\end{array}\right)=Ga$$
通过两个卡尔曼滤波步骤之间的时间差计算delta_t ，而加速度ax， ay是一个均值为0，标准偏差为sigma_ax 和 sigma_ay的随机矢量。

我们将Q定义为过程噪声矢量v的期望值乘以噪声矩阵的转置:
$$Q=E\left[\nu {\nu }^T\right]=E\left[Ga{a}^T{G}^T\right]$$
由于G不包括任何随机变量，因此我们将G移出期望值的计算。
$$Q=GE\left[a{a}^T\right]G^T=G\left(\begin{array}{cc}{\sigma }_{ax}^2& {\sigma }_{axy}\\ {\sigma }_{axy}& {\sigma }_{ay}^2\end{array}\right)G^T=G{Q}_{\nu }{G}^T$$
由于ax，ay互相不相关，这就意味着sigma_axy = 0，我们可以对Qv进一步简化：
$$Q_{\nu }=\left(\begin{array}{cc}{\sigma }_{ax}^2& {\sigma }_{axy}\\ {\sigma }_{axy}& {\sigma }_{ay}^2\end{array}\right)=\left(\begin{array}{cc}{\sigma }_{ax}^2& 0\\ 0& {\sigma }_{ay}^2\end{array}\right)$$
将其带入Q矩阵的计算公式，我们可以得到:
$$Q=G{Q}_{\nu }{G}^T=\left(\begin{array}{cccc}\frac{\Delta t^4}{4}{\sigma }_{ax}^2& 0& \frac{\Delta t^3}{2}{\sigma }_{ax}^2& 0\\ 0& \frac{\Delta t^4}{4}{\sigma }_{ay}^2& 0& \frac{\Delta t^3}{2}{\sigma }_{ay}^2\\ \frac{\Delta t^3}{2}{\sigma }_{ax}^2& 0& \Delta t^2{\sigma }_{ax}^2& 0\\ 0& \frac{\Delta t^3}{2}{\sigma }_{ay}^2& 0& \Delta t^2{\sigma }_{ay}^2\end{array}\right)$$
可以看到，Q 矩阵包含了大量时间delta_t项，这是因为随着时间的推移，我们对自己的位置和速度变得越来越不确定。 随着增量 t 的增加，状态协方差矩阵 P 增加了更多的不确定性。

值得注意的是sigma_ax，sigma_ay 需要根据实际运动模型进行估量，在本项目中我们给定sigma_ax=sigma_ay =3。

• P是状态协方差矩阵，其中包含有关对象位置和速度的不确定性的信息，通常可以认为它包含方差。可又为什么叫做协方差矩阵呢？

我们通过一个实例来理解P的含义：

由于状态向量的元素有n个，因此p矩阵为n x n = 4 x 4。 假设位置Py的幅度变大，Vx速度的幅度也变高，这就意味着Py并Vx具有协方差。如果状态元素之间互相不影响，则可以说它们的协方差为零。如在下图中，如果目标保持横向运动或者纵向运动，Px与Py之间不会相互影响，协方差为0，而当目标斜向运动时，则Px与Py之间会相互影响，协方差不为0。

P 的对角线包含了元素自身的方差，数值越大，代表状态元素的不确定性就越大。 在对角线的周围是两个状态元素之间的协方差，体现了状态元素的值如何相互“共同变化”。 所有像这样的协方差矩阵(如下文中的 R, S, Q)都是对称矩阵，即 Py 和 Vx 的协方差也是 Vx 和Py 的协方差。如下表所示：

	Px	Py	Vx	Vy
Px	Px-variance	A-covariance	D-covariance	F-covariance
Py	A-covariance	Py-variance	B-covariance	E-covariance
Vx	D-covariance	B-covariance	Vx-variance	C-covariance
Vy	F-covariance	E-covariance	C-covariance	Vy-variance

在理解了P矩阵各个成分的含义之后，我们就可以选择合适的参数初始化P矩阵。如果滤波器知道准确的初始位置，则我们可以给出一个各项均为0的初始协方差矩阵。 如
$${\mathbf{P}}_{0|0}=\left[\begin{array}{llcc}0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right]$$
但是这种情况比较少见，一般情况第一次预测是基于已有的测量结果，往往带有噪声。

这种情况下可以尝试用Radar或者Lidar的测量噪声方差来初始化P矩阵。

如果不确切知道最初的位置与速度，那么协方差矩阵可以初始化为一个对角线元素是B的矩阵，B取一个合适的比较大的数。如在本项目中，我们只知道初始状态的位置Px和Py，并不知道速度Vx和Vy, 这种情况下我们可以为Vx-variance和 Vy-variance设置一个较大的初始值。

以下是初始化代码：

is_initialized_ = false;
previous_timestamp_ = 0;
// initializing matrices
R_laser_ = MatrixXd(2, 2);
R_radar_ = MatrixXd(3, 3);
H_laser_ = MatrixXd(2, 4);
Hj_ = MatrixXd(3, 4);
//measurement covariance matrix - laser
R_laser_ << 0.0225, 0,
0, 0.0225;
//measurement covariance matrix - radar
R_radar_ << 0.09, 0, 0,
0, 0.0009, 0,
0, 0, 0.09;
// Initialize P
ekf_.P_ = MatrixXd(4, 4);
ekf_.P_ << 1, 0, 0, 0,
0, 1, 0, 0,
0, 0, 1000, 0,
0, 0, 0, 1000;
H_laser_ << 1, 0, 0, 0,
0, 1, 0, 0;

预测更新代码如下：

x_ = F_ * x_;
MatrixXd Ft = F_.transpose();
P_ = F_ * P_ * Ft + Q_;

测量更新

我们将从两种测量传感器中获取数据：

• 激光测量

• 雷达测量

  1.激光测量

在本项目中，激光测量会获取物体的当前位置，但不提供物体的速度。激光相对于雷达传感器具有更高的空间分辨率，尽管激光传感器也能计算速度，但是准确性不如雷达高。

让我们来看看测量更新x 和 p 的公式：
$$\begin{array}{rl}& 测量残差:y=z-H{x}^{\prime }\\ & 测量残差协方差:S=H{P}^{\prime }{H}^T+R\\ & 最优卡尔曼增益:K=P^{\prime }{H}^T{S}^{-1}\\ & 更新的状态估计:x=x^{\prime }+Ky\\ & 更新的协方差估计:P=(I-KH)P^{\prime }\end{array}$$

我们来分别讨论各个变量的含义：

• 测量矢量z

  对于激光雷达，z 矢量包含位置 x 和位置 y 的测量值。

$$Z=\left(\begin{array}{l}{p}_x\\ p_y\end{array}\right)$$

• 变换矩阵H

  H矩阵是将目标的理论估计状态矢量x’投射到传感器的测空间中的矩阵。对于激光雷达，因为激光雷达传感器仅测量位置，因此我们从状态变量中丢弃速度信息，即状态矢量x包含有关[ px，py，vx，vy ]的信息，而z向量将仅包含[ px，py ]。乘以变换H可以计算传感器真实测量值z与我们的理论估计状态矢量x‘之间的残差。

  对于激光雷达：
  $$\begin{gathered} \left(\begin{array}{l}{p}_x\\ p_y\end{array}\right)=H\left(\begin{array}{l}{p}_x^{\prime }\\ p_y^{\prime }\\ v_x^{\prime }\\ v_y^{\prime }\end{array}\right) \\ H=\left(\begin{array}{llll}1& 0& 0& 0\\ 0& 1& 0& 0\end{array}\right) \end{gathered}$$

• 测量噪声协方差矩阵R

  R矩阵代表传感器测量中的不确定性。R矩阵是正方形，并且矩阵的每一侧与测量参数的数量相同。

  对于激光雷达，我们有一个二维测量矢量。 每个位置成分 px，py 都会受到随机噪声的影响。 所以我们的噪声矢量 ω 和 z 的维数是一样的。测量噪声ω是一个均值为零，协方差为R的分布，即ω∼N(0,R)。因此R矩阵是均值为零的2 x 2协方差矩阵，是噪声矢量 ω 和它的转置乘积的期望值。
  $$R=E\left[\omega {\omega }^T\right]=\left(\begin{array}{cc}{\sigma }_{px}^2& 0\\ 0& {\sigma }_{py}^2\end{array}\right)$$
  注意，非对角线为0表示噪声互不相关。

  通常，随机噪声测量矩阵的参数将由传感器制造商提供，在本项目中已经提供了雷达和激光传感器的R矩阵。

• 测量残差协方差矩阵S

  理论估计值与测量值之间的误差也可以用协方差矩阵S来表示：
  $$\begin{array}{rl}{\mathbf{S}}_t& =\mathrm{cov}\left({\mathbf{z}}_t-\mathbf{H}{\mathbf{x}}_{t|t-1}\right)\\ & =\mathrm{cov}\left(\mathbf{H}{\mathbf{x}}_t+{\mathbf{v}}_t-\mathbf{H}{\mathbf{x}}_{t|t-1}\right)\\ & =\mathrm{cov}\left(\mathbf{H}\left({\mathbf{x}}_t-{\mathbf{x}}_{t|t-1}\right){\mathbf{H}}^{\mathrm{T}}\right)+\mathrm{cov}\left({\mathbf{v}}_t\right)\\ & =\mathbf{H}{\mathbf{P}}_{t|t-1}{\mathbf{H}}^{\mathrm{T}}+{\mathbf{R}}_t\\ & =\mathbf{H}{\mathbf{P}}^{\prime }{\mathbf{H}}^{\mathrm{T}}+\mathbf{R}\end{array}$$

• 测量残差矢量y

  y矢量是实际测量值和预测估计值之间的残差。

• 卡尔曼增益K

  卡尔曼滤波的思想是分别给预测估计值和实际测量值一个权重，通过预测估计值与实际测量值的加权线性组合来得到估计值，即：
  $$\begin{gathered} {\mathbf{x}}_{t|t}={\mathbf{K}}_t{\mathbf{z}}_t+\left(\mathbf{I}-{\mathbf{K}}_t\mathbf{H}\right){\mathbf{x}}_{t|t-1} \\ {\mathbf{x}}_{t|t}={\mathbf{x}}_{t|t-1}+{\mathbf{K}}_t({\mathbf{z}}_t-\mathbf{H}{\mathbf{x}}_{t|t-1}) \\ x=x^{\prime }+Ky \\ P=(I-KH)P^{\prime } \end{gathered}$$
  卡尔曼增益 k是给予给矢量y的权重，包含了预测估计值 x‘和当前观测值 z 的权重信息，用来继续更新状态矢量x和状态协方差矩阵 P。一般来说，较低的权重赋予较高的不确定性。也就是说如果我们的传感器测量是非常不确定的(R高于P′ ) ，那么卡尔曼滤波器将给予更多的权重给我们认为的状态估计x′。 如果我们的状态估计是不确定的(P′高于R) ，卡尔曼滤波器会把更多的权重给传感器测量值 z。

  激光雷达更新代码如下：

  void KalmanFilter::Update(const VectorXd &z) {
      /**
       * TODO: update the state by using Kalman Filter equations
       */
      VectorXd z_pred = H_ * x_;
      VectorXd y = z - z_pred;;
      MatrixXd Ht = H_.transpose();
      MatrixXd S = H_ * P_ * Ht + R_;
      MatrixXd Si = S.inverse();
      MatrixXd K = P_ * Ht * Si;
  
      x_ = x_ + K * y;
      int x_size = x_.size();
      MatrixXd I = MatrixXd::Identity(x_size, x_size);
      P_ = (I - K * H_) * P_;
  }
  

  2. 雷达测量

尽管激光传感器能提供准确的行人位置数据，但实际上我们无法直接观察其速度，这个时候我们就需要雷达了。根据多普勒效应，雷达能够得到直接测量移动对象的径向速度。径向速度是指对象靠近或者远离传感器的移动速度。但是雷达提供的测量结果是包含距离，角度和距离速率的极坐标数值，我们需要转换成X状态矢量所在的笛卡尔坐标，这一转换是非线性的，我们无法通过传统卡尔曼滤波实现，我将在扩展卡尔曼滤波中详细解释这一部分。

Extended Kalman Filter

在上文中，我们已经把激光测量值整合到卡尔曼滤波中，但是雷达测量值并不是一样的整合方式。

原因是雷达观察世界的方式是不同的。

• 距离ρ是原点到目标的径向距离，可以定义为 ρ=sqrt(px2+py2)。

• 方向角φ射线与x方向的夹角，φ=atan(py/px)。请注意，φ是以x轴逆时针为正参考方向的，因此上述图中φ实际上为负。

• 距离变化率ρ是速度v在沿着射线L方向上的投影，也被称做径向速度。

激光测量的H矩阵和雷达测量的h(x)方程实际上是在完成相同的工作。它们都需要在更新步骤中解*y* = z - Hx'等式。

但是对于雷达，没有H矩阵可以将状态向量x映射到极坐标中，需要手动计算映射以将笛卡尔坐标转换为极坐标。

下面是h(x)函数，它指定如何将预测的位置和速度映射到距离，角度和距离变化率的极坐标。

下图是笛卡尔坐标转换极坐标的方法：

因此，对于雷达，y = z - Hx '等式变成了y = z - h(x')。

现在我已经有了一个非线性测量函数h(x)，如果我们想用新的测量值z更新预测状态x*，我们能否继续使用卡尔曼滤波方程式了呢？

答案是否定的，原因是：我们的预测状态x已经由高斯分布表示，如果我们将该分布映射到上述的非线性函数h(x)，那么所得函数将不是高斯函数。

务必注意卡尔曼滤波器仅适用于高斯函数。

这个时候就需要引入非线性处理函数：扩展卡尔曼滤波。

h(x)函数线性化是扩展卡尔曼滤波器(EKF)的关键。

EKF将当前估计值的平均值周围的分布线性化，即在原始高斯分布的均值位置，用一个和h(x)相切的线性函数，近似出测量值函数，然后在卡尔曼滤波器算法的预测和更新状态中使用此线性化。

如上图所示，非线性函数的分布不是高斯分布。

而在下图中，对非线性函数进行近似线性化得到的分布是高斯分布。

EKF 使用一种称为“ **一阶泰勒展开”**的方法来线性化函数。
$$h(x)\approx h(\mu )+\frac{\partial h(\mu )}{\partial x}(x-\mu )$$
函数h(x)对应于x的导数被称为雅可比矩阵，它包含所有偏导数。对于雅可比矩阵的推导稍显复杂，在此我直接给出结果。感兴趣的朋友可以对h(x)一一求偏导数。
$$H_j=\left[\begin{array}{cccc}\frac{\partial \rho }{\partial p_x}& \frac{\partial \rho }{\partial p_y}& \frac{\partial \rho }{\partial v_x}& \frac{\partial \rho }{\partial v_y}\\ \frac{\partial \phi }{\partial p_x}& \frac{\partial \phi }{\partial p_y}& \frac{\partial \phi }{\partial v_x}& \frac{\partial \phi }{\partial v_y}\\ \frac{\partial \dot{\rho }}{\partial p_x}& \frac{\partial \dot{\rho }}{\partial p_y}& \frac{\partial \dot{\rho }}{\partial v_x}& \frac{\partial \rho }{\partial v_y}\end{array}\right]=\left[\begin{array}{cccc}\frac{p_x}{\sqrt{p_x^2+p_y^2}}& \frac{p_y}{\sqrt{p_x^2+p_y^2}}& 0& 0\\ -\frac{p_y}{p_x^2+p_y^2}& \frac{p_x}{p_x^2+p_y^2}& 0& 0\\ \frac{p_y\left(v_x{p}_y-v_y{p}_x\right)}{{\left(p_x^2+p_y^2\right)}^{3/2}}& \frac{p_x\left(v_y{p}_x-v_x{p}_y\right)}{{\left(p_x^2+p_y^2\right)}^{3/2}}& \frac{p_x}{\sqrt{p_x^2+p_y^2}}& \frac{p_y}{\sqrt{p_x^2+p_y^2}}\end{array}\right]$$
虽然数学证明看起来有些复杂，但是卡尔曼滤波方程和扩展卡尔曼滤波器方程是非常相似的。

主要区别在于如果单独只对非线性模型变量完成预测和更新：

• 计算P ’ 时，F 矩阵将被 Fj 替换。
• 计算S，K 和 P时，将用雅可比矩阵Hj替换卡尔曼滤波器中的H矩阵。
• 为了计算x '，使用预测更新函数 f 代替 F 矩阵。
• 为了计算y，使用 h 函数代替 H 矩阵。

如果我们在只对非线性模型进行估计最优化，我们需要在预测和测量更新步骤中都使用非线性模型等式，意味着我们在预测中也需要用它的雅可比矩阵Fj 来代替 F 矩阵，如我们只用雷达完成位置速度的最优估计。

但是在本项目中，由于我们的目的是融合激光和雷达传感器，激光雷达使用线性模型，因此我们在两个传感器各自的预测中都不使用 f 函数或 Fj函数，仍然使用常规的卡尔曼滤波方程和 F 矩阵。对于测量更新的步骤，则根据传感器的不同选择卡尔曼滤波方程或者扩展卡尔曼滤波方程。

雷达更新代码如下：

void KalmanFilter::UpdateEKF(const VectorXd &z) {
    /**
     * TODO: update the state by using Extended Kalman Filter equations
     */
    double px = x_(0);
    double py = x_(1);
    double vx = x_(2);
    double vy = x_(3);
    // Coordinate conversion from Cartesian coordinates to Polar coordinates
    double rho = sqrt(px*px + py*py);
    double theta = atan2(py, px);
    double rho_dot = (px*vx + py*vy) / rho;
    VectorXd h = VectorXd(3);
    h << rho, theta, rho_dot;
    VectorXd y = z - h;
    // Nominalization of angle
    while (y(1)>M_PI) y(1)-=2*M_PI;
    while (y(1)<-M_PI) y(1)+=2*M_PI;

    MatrixXd Ht = H_.transpose();
    MatrixXd S = H_ * P_ * Ht + R_;
    MatrixXd Si = S.inverse();
    MatrixXd K =  P_ * Ht * Si;

    x_ = x_ + (K * y);
    int x_size = x_.size();
    MatrixXd I = MatrixXd::Identity(x_size, x_size);
    P_ = (I - K * H_) * P_;

}

至此我们完成了卡尔曼滤波和扩展卡尔曼滤波的原理讲解，现在来让我们看下激光和雷达传感器融合的流程。

Sensor fusion framework

这是激光和雷达传感器融合的整体处理流程：

• 首次测量 -卡尔曼滤波器将接收目标相对于汽车位置的初始测量值。这些测量值来自雷达或激光雷达传感器。

• 初始化状态和协方差矩阵 -卡尔曼滤波器将基于第一次测量值来初始化目标的位置。

• Δ t 时间后，汽车将收到另一个传感器测量值。

• 预测 -算法将预测Δ t 时间后的目标位置。预测自行车位置的一种方式是假设自行车的速度是恒定的，Δ t 时间后目标将移动v * Δ t 距离。在本扩展卡尔曼滤波项目中，我们将假设速度是恒定的。

• 更新 -滤波器将预测的位置与传感器测量值进行比较。将预测的位置和测量的位置合并以给出更新的位置。卡尔曼滤波器将根据每个值的不确定性将更多的权重放在预测位置或测量位置上。

  • 如果当前观察数据来自雷达传感器，我们使用雷达的H和R矩阵来设置扩展卡尔曼滤波器，而且我们必须计算新的雅可比矩阵Hj，使用非线性函数来变化坐标系，并调用测量更新。
  • 如果当前观察数据来自激光雷达，我们使用激光雷达的H和R矩阵来设置卡尔曼滤波器，然后调用测量更新。

• Δ t 时间后，汽车又收到另一个传感器测量值。算法将开始执行下一个预测和更新步骤。

  

Evaluation Kalman Filter Performance

在我们实现了追踪算法之后，我们需要检查算法效果，来评估估算结果和真实结果差别有多大。

最常见的检查标准叫做均方根误差(Root mean squared error)。
$$RMSE=\sqrt{\frac{1}{n}\sum _{t=1}^n{\left(x_t^{est}-x_t^{true}\right)}^2}$$
估算状态和真实状态之间的差值叫做残差。对这些残差先平方然后求均值就可以得到均方根误差。

在本项目中，真实状态的值已经给出。

均方根误差评估代码如下:

MatrixXd Tools::CalculateJacobian(const VectorXd& x_state) {
  /**
   * TODO:
   * Calculate a Jacobian here.
   */
    MatrixXd Hj(3,4);
   // state parameters
    double px = x_state(0);
    double py = x_state(1);
    double vx = x_state(2);
    double vy = x_state(3);

    // preparation of Jacobian terms
    double c1 = px*px+py*py;
    double c2 = sqrt(c1);
    double c3 = (c1*c2);

    if(fabs(c1) < 0.0001){
        cout << "ERROR - Division by Zero" << endl;
        return Hj;
    }
    // compute jacobian matrix
    Hj << (px/c2), (py/c2), 0, 0,
            -(py/c1), (px/c1), 0, 0,
            py*(vx*py - vy*px)/c3, px*(px*vy - py*vx)/c3, px/c2, py/c2;

    return Hj;

}

Conclusion

• 卡尔曼滤波虽然计算复杂度低，但是仅能解决线性问题，对于非线性问题，需要使用扩展卡尔曼滤波等算法。
• 尽管扩展卡尔曼滤波能解决非线性问题，但是仍有一些缺点：
  • 如果需要用解析方法求雅可比矩阵，则计算很困难的。
  • 如果用数值分析的方法求出雅可比矩阵，则计算开销很大。
  • 扩展卡尔曼滤波器只适用于具有可微分模型的系统。
• 由于雷达测量是非线性的，因此我们需要在雷达测量更新周期中使用扩展卡尔曼滤波器，而激光测量是线性的，我们在激光测量更新中使用卡尔曼滤波器，在预测周期中两者都可以使用相同的卡尔曼滤波器公式。

在下一篇博客中我会介绍无迹卡尔曼滤波(UKF），这是一种更强大的处理非线性模型的卡尔曼滤波变种。

实际上Unscented Kalman Filter应该被翻译成无味卡尔曼滤波，因为作者当年就是觉得扩展卡尔曼滤波太没意思了，才发明了Unscented Kalman Filter !

如果有什么疑问，可以随时联系我的个人邮箱。

如果你觉得我的文章对你有帮助，请帮忙点个赞～＼（≧▽≦）／～

转载请私信作者！

引用：

• Udacity
• Wiki