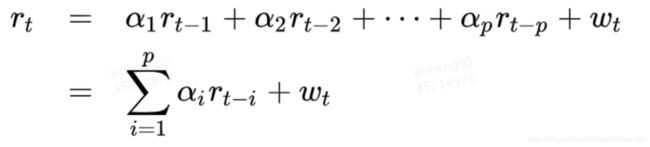ARIMA学习

目录

 

1 ARIMA理论介绍

1.1 模型构成

1.1.1 AR模型

1.1.2 MA模型

1.1.3 ARMA模型

1.1.4 I差分

1.2 模型定阶

2 模型分析

2.1 是否选择ARIMA模型

2.1.1 Prophet

2.1.2 holt-winter模型

2.1.3 ARIMA模型

2.2 实现方式

2.2.1 Python实现

2.2.2 Java实现

2.2.3 使用步骤

3 模型实践

3.1 订单预测

3.2 其他预测

8 问题

9 参考资料

---

1 ARIMA理论介绍

1.1 模型构成

ARIMA模型是由三部分组成的，AR模型    I差分    MA模型。ARMA模型要求序列是平稳序列，因为可以对序列进行平稳性处理[1](最常见就是差分处理)。

1.1.1 AR模型

1 基本思想

AR模型的基本思想是：该模型认为通过时间序列过去时点的线性组合加上白噪声即可预测当前时点，它是随机游走的一个简单扩展。 历史若若干期的数据(侧重) + 白噪声

 

Xt表示t时间点的数据。

2 使用要求

自回归模型要求序列是平稳序列，一般对于一个有规律的序列，剔除了长期趋势和季节因素和随机因素。然后就可以用AR模型来建模。

AR(p) p表示滞后p阶的AR模型，当前时间点与前p个时间点的关系。p=1，当前时间和前1个时间点的关系。

3 相对于普通回归的特点

AR是一种自回归模式，AR仅通过时间序列变量的自身历史观测值来反映有关因素对预测目标的影响和作用，不受模型变量相互独立的假设条件约束，所构成的模型可以消除普通回归预测方法中由于自变量选择、多重共线性等造成的困难。

Note:

白噪声：白噪声是指功率谱密度在整个频域内均匀分布的噪声

自回归：AutoRegressive自回归，描述当前值和历史值之间的关系。

平稳序列： 见1.1.3

1.1.2 MA模型

MA模型的基本思想是用过去各个时期的随机干扰或预测误差的线性组合来表达当前预测值。 一个常数+历史误差(侧重)

（Moving average滑动平均，描述误差之间的关系）描述自回归部分的误差累计。

 

MA(q) q表示前q个时间点的时间差

1.1.3 ARMA模型

1 业务意义举例

上述两节简述了前面AR和MA模型的概况，这两个模型并不是偶然出现，背后其实是有实际业务场景意义的。

比如“前者用收益率的历史对未来收益率做预测，它背后的逻辑是捕捉市场参与者的有效性（或者非有效性）造成的市场的动量或者反转效应；而后者对噪声建模，其逻辑为突发信息对收益率将会造成冲击（比如上市公司超出预期的财报或者内部交易丑闻等）"。

以上引自：https://zhuanlan.zhihu.com/p/38322333

2 ARMA模型

上述两节简述了前面AR和MA模型的概况，很自然我们能想到将两者结合到一块，这样既能利用历史数据，又能考虑历史误差。用AR的历史项+MA的误差。

Note:这是一个新的模型，并不是说将两者的各自所有的参数都求出来再相加，如若这样大约就是原值的两倍，这肯定不是科学的。

1.1.4 I差分

差分值有 观测 + 检验 法来确定

   怎么数据判断是否平稳呢？这里使用简单点的根据数据的 均值 和 方差 来做判断。如果两者都处于平稳那么，就处于弱平稳了。差分的方法就是做差：一个数据序列r2、r3、r4、r5、rn减去r1、r2、r3、r4、rn-1的来获取差值序列。这是一阶差分，利用获得的差序再做差分，就是二阶差分。 I(d)    d表示做多少阶的差分。

Note:

1 当然也可以使用ARMA模型，由于ARMA模型需要平稳的时间序列，或者转化为弱平稳时间序列。所以ARMA模型中引入I差分，构成了ARIMA模型。ARIMA模型需要引入三个变量参数p、d、q

2 季节效应，序列的季节因素和我们常说序列的周期性其实是在表达两个问题。季节效应潜在的语境并不是说多年中每年中的这个季节都呈现这个序列趋势，而是在我们研究的序列中季节因素导致某一段数据变化很大导致序列不平稳，我们需要剔除这个因素，从而达到平稳序列。

1.2 模型定阶

Arima的Python实现包是基于statsmodels的，而其中的ARIMA（p，d，q），d不能>2。具体是几阶，得看单位根检验结果。

p和q的确定可以基于AIC思想。

基本思想：AIC

过程：略

 

2 模型分析

2.1 是否选择ARIMA模型

目前时序预测使用较多的有三种模型，ARIMA、winter模型以及Facebook的Prophet模型。既然定位在时序分析的范畴，其理论基础就是数据之间的时序关系。如果某场景数据本身的时序关系就不强(比如股公司股票，收到政策，社会事件，公司运营等无规律因素的影响)，那么就不应该用时序方法来分析。

2.1.1 Prophet

先说下Facebook的Prophet模型，这个模型有如下特点：

1 安装简单，使用简单，paper和title对prophet的宗旨已经有所阐述。降低预测门槛。无需调参，对异常数据的鲁棒性也很好

2 本质上还是一个加法模型，是时间序列预测的一个工业级应用，最初用来在Facebook执行商业预测，在原理上并没有什么创新。

3 使用场景：数据量比较大，时间跨度大效果比较好

4 简单易用：傻瓜式建模、预测，都是简单调用，无需调参。

5 对有明显规律的数据的效果好，对规律不那么明显的数据，效果不尽人意。

其实也不是什么缺点，Prophet的paper和title对prophet的宗旨已经有所阐述。降低预测门槛，尽量在大部分场景下都能得到一个用户差不多能接受的结果。这种情况下可以作为baseLine

2.1.2 holt-winter模型

winter模型本质上是三次指数平滑

温特模型预测订单：https://tech.meituan.com/order_holtwinter.html

2.1.3 ARIMA模型

使用场景：

2.2 实现方式

2.2.1 Python实现

statsmodels包中含有ARMA模型和ARIMA模型

from statsmodels.tsa.arima_model 
import ARMA 
model = ARMA(timeseries, order=order.bic_min_order) result_arma = model.fit(disp=-1, method='css')

对于差分后的时间序列，运用于ARMA时该模型就被称为ARMIA，在代码层面改写为model = ARIMA(timeseries, order=(p,d,q))，但是实际上，用差分过的序列直接进行ARMA建模更方便，之后添加一步还原的操作即可。简单来说，如果将序列已经差分好，直接使用arma模型；如果没有差分好，自己算好差分，将原始数据传入模型，给差分数，其实就是让ARIMA模型自行先算一次差分，本质都是一样的

 

2.2.2 Java实现

https://github.com/chenchen199427/ARMA-Java-

2.2.3 使用步骤

1. 数据预处理

2. 差分及平稳性校验(确定参数d)

3. 输出ACF和PACF图，确定p和q的值

4. 运用模型进行预测

5. 还原差分运算，得到最终预测数据

3 模型实践

3.1 订单预测

数据来源：半年的外卖订单量

预处理：没有异常数据，

数据探查：趋势图

 

数据的特点是，周一至周五基本持平没有一个明显的规律，周末叫工作日的波动幅度在 2%左右。而且数据有非常微弱的长期趋势。

使用了从6.1日到10.12(周五)的数据预测周六，最终数据和实际值差7% 感觉效果一般。

从6.1日到9.12日(周五)数据预测接下来的周六，最终数据和实际值差5% 效果较之前有进步，个人觉得10.12日之前是国庆节七天，数据不符合普通的规律性，会给预测带来一定的偏差。

由于日订单数据的特点就是

3.2 其他预测

8 问题

ARIMA和winter的从原理上来说特点如何？如何决定各自的具体适用场景？如何选择？

9 参考资料

1 [不平稳处理] https://www.jianshu.com/p/cced6617b423

2 [ar和ma的含义 写的不错，推荐] https://zhuanlan.zhihu.com/p/38322333

3 [ss] https://www.jianshu.com/p/cced6617b423

4 [git java实现代码] https://github.com/chenchen199427/ARMA-Java-

5 [java实现] https://blog.csdn.net/u013201628/article/details/62236654