数据分析笔试题
数据分析笔试题
网易数据分析
1. 通常可以通过关联规则挖掘来发现啤酒和尿布的关系, 那么如果对于一条规则A →B, 如果同时购买A和B的顾客比例是4/7, 而购买A的顾客当中也购买了B的顾客比例是1/2, 而购买B的顾客当中也购买了A的顾客比例是1/3,则以下对于规则A →B的支持度(support)和置信度(confidence)分别是多少?
知识点
关联规则 支持度 置信度
笔记
关联规则:反映一个事物与其他事物之间的相互依存性和关联性
常用的频繁项集的评估标准有支持度,置信度和提升度
支持度:几个关联的数据在数据集中出现的次数占总数据集的比重,即项集出现的比例
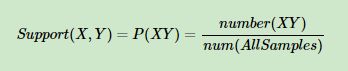
置信度:一个数据出现后,另一个数据出现的概率,即条件概率
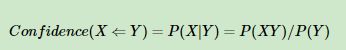
提升度:表示含有Y的条件下,同时含有X的概率,与X总体发生的概率之比
![]()
解答
本体中规则A →B的支持度是同时购买AB的比例,即4/7,置信度是购买A的人中购买B的比例,即1/2
2.设{xn}服从独立同分布, E[xn] = 0, Var[xn]=1, 则当n趋向于无穷大时,下式值为:
![]()
知识点 概率论
分析
独立同分布,相关系数为0,对式子取期望
E(X2)=E2(X)+Var(X)=1;
E(Xi, Xi+1)=0;
3.最小二乘估计是线性无偏估计中方差最小的
知识点 无偏估计 最小二乘
4.小明在一次班干部二人竞选中,支持率为百分之五十五,而置信水平0.95以上的置信区间为百分之五十到百分之六十,请问小明未当选的可能性有可能是
知识点 统计 假设检验
分析
置信水平0.95以上的置信区间为50%-60%,则区间[0%, 50%]⋃[60%,100%]的概率为5%。
仅当落在区间区间[0%, 50%]时,小明落选,则概率为
(50-0)((50-0)+(100-60) * 5% = 5/9 * 5% ≈ 2.78% ≈ 3%
双尾 双尾5% 单尾肯定小于5%
5.一个快递公司对同一年龄段的员工,进行汽车,三轮车,二轮车平均送件量的比较,结果给出sig.=0.034,说明
知识点 假设检验 统计
分析
p值表示接受原假设最小的显著性水平,p值越小,拒绝原假设的理由越充分
6.以下关于python数据结构说法正确的是
知识点 tuple dict list
笔记
list
1.列表(链表的数据结构)有序的项目, 通过索引进行查找,使用方括号”[]”
2.list可以动态更新,也可以进行嵌套.
tuple
1.将整个元素集是用小括号括起来,是有序集合
2.tuple是不可变的list,创建了一个tuple就不能以任何方式改变它
3.没有 append、extend、remove或pop方法以及index方法
dict
1.整个元素集合用大括号括起来,有序集合
2.键可以是数字、字符串或者是元组等不可变类型
set
1.set是建立一系列无序的,不重复的元素
2.创建set的方式是调用set()并传入一个list,list的元素将作为set的元素set([])
注意 python3.6后的版本,dict中的键值对是有序的,之前版本无序
7.若要在员工信息表EMP中增加一列WANGYI_NO(网易id),可用( )

8.对于SQL语句select * from t where a=100 and b=200,哪个索引可以使用到()

知识点 SQL 索引
笔记
1.复合索引:Mysql从左到右的使用索引中的字段,一个查询可以只使用索引中的一部份,但只能是最左侧部分。例如索引是key index (a,b,c). 可以支持a | a,b| a,b,c 3种组合进行查找,但不支持 b,c进行查找 .当最左侧字段是常量引用时,索引就十分有效
2. sql条件查询+排序 适合加索引
9.哪个不是DDL(数据库定义语言)语句?
知识点 数据库语言类型
笔记
DDL语法:
创建:create
删除:drop
修改:alter
修改表名:rename table 旧表名 to 新表名
数据库控制语言DCL:
grant授权
10.截取logfile文件中含有suc的行,并且只输出最后一列,下列操作正确的是:

知识点 linux grep awk
germ
Linux系统中grep命令是一种强大的文本搜索工具,它能使用正则表达式搜索文本,并把匹 配的行打印出来
1.-o 只输出文件中匹配到的部分
2.匹配符 *
 3.通过"-v"参数可以打印出不符合条件行的内容
3.通过"-v"参数可以打印出不符合条件行的内容
awk
常用形式awk ‘{pattern + action}’ {filenames}
pattern 表示 AWK 在数据中查找的内容,而 action 是在找到匹配内容时所执行的一系列命令
awk ‘{print $NF}’ : 打印每行中的最后一个字段
11.将当前命令sh test.sh任务在后台执行,下列最优雅的的做法是
知识点
Linux
分析
nohup (no hang up)命令
用途:不挂断地运行命令。
语法:nohup Command [ Arg … ] [ & ]
例子: nohup sh example.sh &
描述:nohup 命令运行由 Command 参数和任何相关的 Arg 参数指定的命令,忽略所有挂断(SIGHUP)信号。在注销后使用 nohup 命令运行后台中的程序。要运行后台中的 nohup 命令,添加 & ( 表示”and”的符号)到命令的尾部
12.将一个整数序列整理为升序,两趟处理后序列变为10,12,21,9,7,3,4,25,则采用的排序算法可能是________。
知识点 排序算法
笔记
- 冒泡:i*j 两两比较,小的放前
- 选择:i*j两两比较,遍历j后,找到最小的放前面
- 插入:默认第一个排好序(只有一个,也没得比较),第一步:第二个与第一个比较排序;第二步:第三个插入前面排好序的序列;第三步,第四个插入前面的序列,以此类推
- 希尔:类似插入排序,但第一步:分i//2堆(随机分配)同步进行插入排序(第一堆排完,再第二堆,再第三堆…);第二步:分i//4堆依次排;…最后一步:一整堆进行插入排序,耗时i;
- 归并:分而治之,dynamic programming
- 快排:定义分区函数,主函数递归排序
- 堆排:建立二叉树,树内排序,找到最大值取出,更新树,再取出第二大的数…以此类推
- 计数:不用比较,牺牲空间换时间,开辟key为min到max的数组,遍历原序列,统计数的个数;再对key按顺序输出即可。
- 桶排:计数排序的升级,计数用了max-min+1个桶,桶排序用k个桶(数量更少),桶内排好序(用传统方法,或递归用桶排),再对桶按顺序输出即可。
- 基数:同样基于计数排序,先按个位数入列(0-9个列),排好第一步;再按十位数入列,排好第二步;…依次到最大位数入列,排好输出即可。
分析
插入排序:第n趟前n+1个有序
选择排序:第n趟前n个位置正确
快速排序:第n趟有n个元素位置正确
堆排序:第n趟前或后n个位置正确
13.若有33个长度不等的初始归并段,做7路平衡归并排序,为组织最佳归并树,应增加长度为0的初始归并段的个数是________。

知识点 平衡归并排序
笔记
1.插入排序、选择排序、归并排序等等,这些算法都属于内部排序算法,即排序的整个过程只是在内存中完成
2.当待排序的文件比内存的可使用容量还大时,文件无法一次性放到内存中进行排序,需要借助于外部存储器(例如硬盘、U盘、光盘),这时就需要外部排序算法来解决
3.外部排序算法由两个阶段构成:
按照内存大小,将大文件分成若干长度为 l 的子文件(l 应小于内存的可使用容量),然后将各个子文件依次读入内存,使用适当的内部排序算法对其进行排序(排好序的子文件统称为“归并段”或者“顺段”),将排好序的归并段重新写入外存,为下一个子文件排序腾出内存空间;
对得到的顺段进行合并,直至得到整个有序的文件为止。
4.例如:有 10 个初始归并段到一个有序文件,共进行了 4 次归并,每次都由 m 个归并段得到 ⌈m/2⌉ 个归并段,这种归并方式被称为 2-路平衡归并
5.对于外部排序算法来说,影响整体排序效率的因素主要取决于读写外存的次数,即访问外存的次数越多,算法花费的时间就越多,效率就越低。
6.一般情况下对于具有 m 个初始归并段进行 k-路平衡归并时,归并的次数为:s=⌊logkm ⌋(其中 s 表示归并次数)
7.对于如何减少访问外存的次数的问题,就等同于考虑如何使 k-路归并所构成的 k 叉树的带权路径长度最短
8.若想使树的带权路径长度和最短,就是构造赫夫曼树,通过以构建赫夫曼树的方式构建归并树,使其对读写外存的次数降至最低(k-路平衡归并,需要选取合适的 k 值,构建赫夫曼树作为归并树)。所以称此归并树为最佳归并树。
9.在一般情况下,对于 k–路平衡归并来说,若 (m-1)MOD(k-1)=0,则不需要增加虚段;否则需附加 k-(m-1)MOD(k-1)-1 个虚段
14.将4个不一样的球随机放入5个杯子中,则杯子中球的最大个数为3的概率是?
知识点 概率
分析
前三个球有针对的放,概率为(1/5)(1/5)(1/5)
选定盛装三个球的杯子:5个可能
最后一个球放的杯子有四种选择:4个可能
四种球不同,最后一个球的可能性为4个可能
[5*(1/5)(1/5)(1/5)]*(4/5)*4=16/125
15.从数字集合{1,2,3,4,… ,20}中选出4个数字的子集,如果不允许两个相连的数字出现在同一集合中,那么能够形成多少个这种子集?
知识点 概率 排列组合 插空法
分析
插空法 ,把4个数插到16个数形成的17个空格中
笔记
某些元素不相邻的排列组合题,即不邻问题,可采用插空法,即在解决对于某几个元素要求不相邻的问题时,先将其它元素排好,再将指定的不相邻的元素插入已排好元素的间隙或两端位置
1.基本题型为:n个相同元素,不同个m组,每组至少有一个元素;求共有多少种不同方法?
答:在 n 个元素的n-1 个间隙中放置 m-1 块隔板把它隔成 m 份
2.有 n 个相同的元素,要求分到 m 组中,问有多少种不同的分法?
答:这种问题是允许有些组中分到的元素为 “0”,也就是组中可以为空的。对于这样的题,我们就首先将每组都填上 1 个,这样所要元素总数就 m 个,问题也就是转变成将( n+m )个元素分到 m 组,并且每组至少分到一个的问题,也就可以用插板法来解决。
16.有2堆宝石,A和B一起玩游戏,假设俩人足够聪明,规则是每个人只能从一堆选走1个或2个或3个宝石,最后全部取玩的人获胜,假设2堆宝石的数目为12和13,请问A怎么可以必胜?
知识点 博弈
笔记
面对平衡态(奇异态)的输,面对非平衡态赢,(12,13)相当于(0,n),一次取n,此时为非平衡态,先取的赢。
取石子游戏
问题介绍:一个古老的博弈游戏,发源于中国,它是组合数学领域的一个经典问题。它有许多不同的玩法,基本上是两个玩家,玩的形式是轮流抓石子,胜利的标准是抓走了最后的石子。
玩家设定: 先取石子的是玩家A,后取石子的是玩家B。
经典的三种玩法:
1.巴什博奕(Bash Game):有1堆含n个石子,两个人轮流从这堆物品中取物,规定每次至少取1个,最多取m个。取走最后石子的人获胜。
2.尼姆博奕(Nimm Game),有k堆各n个石子,两个人轮流从某一堆取任意多的物品,规定每次至少取一个,多者不限。取走最后石子的人获胜。
3.威佐夫博奕(Wythoff Game),有2堆各n个石子,两个人轮流从某一堆或同时从两堆中取同样多的物品,规定每次至少取1个,多者不限。取走最后石子的人获胜。
解析:平衡状态,又称作奇异局势。当面对这个局势时则会失败。任意非平衡态经过一次操作可以变为平衡态。每个玩家都会努力使自己抓完石子之后的局势为平衡,将这个平衡局势留给对方。因此,玩家A能够在初始为非平衡的游戏中取胜,玩家B能够在初始为平衡的游戏中取胜。
玩法一:
显然,如果n=m+1,那么由于一次最多只能取m个,所以,无论先取者拿走多少个,后取者都能够一次拿走剩余的物品,后者取胜。因此我们发现了如何取胜的法则:如果n=(m+1)r+s,(r为任意自然数,s≤m),那么先取者要拿走s个物品,如果后取者拿走k(≤m)个,那么先取者再拿走m+1-k个,结果剩下(m+1)(r-1)个,以后保持这样的取法,那么先取者肯定获胜。总之,要保持给对手留下(m+1)的倍数,就能最后获胜。
即,若n=k*(m+1),则后取者胜,反之,存在先取者获胜的取法。n%(m+1)=0. 先取者必败
奇异局势是n=(m+1)*i,玩家的策略是若当前的石子个数为(m+1)*i+s,那么就将s个石子取走,使其达到奇异局势。
玩法二:
https://blog.csdn.net/petersmart123/article/details/69058910
分析
A先拿,拿走13个里的一个, 然后B拿1个,A就拿同堆的3个,B拿2个,A就拿同堆的2个,B拿3个,A就拿同堆的1个
17 编程题
小易有一些彩色的砖块。每种颜色由一个大写字母表示。各个颜色砖块看起来都完全一样。现在有一个给定的字符串s,s中每个字符代表小易的某个砖块的颜色。小易想把他所有的砖块排成一行。如果最多存在一对不同颜色的相邻砖块,那么这行砖块就很漂亮的。请你帮助小易计算有多少种方式将他所有砖块排成漂亮的一行。(如果两种方式所对应的砖块颜色序列是相同的,那么认为这两种方式是一样的。)
例如: s = “ABAB”,那么小易有六种排列的结果:
“AABB”,“ABAB”,“ABBA”,“BAAB”,“BABA”,“BBAA”
其中只有"AABB"和"BBAA"满足最多只有一对不同颜色的相邻砖块。
笔记全排列问题 剑指offer
18.编程题
小易为了向他的父母表现他已经长大独立了,他决定搬出去自己居住一段时间。一个人生活增加了许多花费: 小易每天必须吃一个水果并且需要每天支付x元的房屋租金。当前小易手中已经有f个水果和d元钱,小易也能去商店购买一些水果,商店每个水果售卖p元。小易为了表现他独立生活的能力,希望能独立生活的时间越长越好,小易希望你来帮他计算一下他最多能独立生活多少天。
