正则化（regularization）： 期望风险、经验风险、结构风险、L0范数、L1范数、L2范数

正则化（regularization）：

期望风险、经验风险、结构风险、L0范数、L1范数、L2范数

• 主要内容
  
  • 期望风险、经验风险、结构风险
  • 正则项：L0范数、L1范数、L2范数
  • 关于L1正则化与L2正则化的问题整理

---

一、期望风险（expected risk）、经验风险（empirical risk）、结构风险（structural risk）
  1、期望风险（expected risk）
  期望风险（expected risk）：描述模型与训练样本以及测试样本（或者称之为“未知样本”）的拟合程度。表示如下：

L(Y,f(X)) 表示损失函数，损失函数值越小，说明模型对样本（训练样本以及测试样本）的拟合程度越好。 P(X,Y) 表示 X 与 Y 的联合概率分布。对于训练样本，我们知道 X 与 Y 的联合概率分布；但是，对于测试样本（未知样本），我们并不知道 X 与 Y 的联合概率分布。因为，如果我们知道测试样本（未知样本） X 与 Y 的联合概率分布，我们就可以得到 X 与 Y 的条件概率分布 P(Y|X) ，那么我们就不用学习模型啦，直接针对测试样本（未知样本）求解 P(Y|X) 就行啦。显然，工程实践中，没这么简单的事情。
  因此，针对期望风险，我们并不能够直接求解得到。
  但是，机器学习中，针对模型的选择，我们需要选择期望风险最小的模型，如果无法得到期望风险，我们是否就无法进行模型的选择了呢？答案是否定的。

  2、经验风险（empirical risk）
  经验风险（empirical risk）：描述模型与训练样本的拟合程度。表示如下：

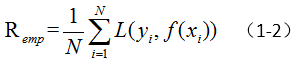
其中， L(Y,f(X)) 表示损失函数， N 表示训练样本的个数。
  因此，针对经验风险，我们是能够直接求解得到的。经验风险越小，说明模型对训练样本的拟合程度越高；经验风险越大，说明模型对训练样本的拟合程度越低。
  针对训练样本时，我们希望经验风险最小，说明模型能够很好的拟合训练样本；但是，此时模型针对测试样本，可能并不能产生很好的拟合效果；这说明，此时，我们的模型有可能过拟合了。
  经验风险越小，说明我们的模型需要更多的参数来拟合训练样本，导致模型的复杂程度变高，导致模型的泛化能力变弱，从而导致过拟合。为了解决这一问题，我们需要限制模型的复杂程度，从而使得我们的模型不仅能够比较优秀的拟合训练样本，而且能够具备比较优秀的泛化能力，以此达到期望风险的效果，进行模型的选择。

  3、结构风险（structural risk）
  结构风险（structural risk）：描述模型与训练样本的拟合程度，以及模型的复杂程度。表示如下：

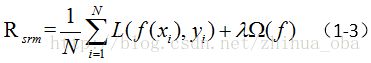
其中， L(Y,f(X)) 表示损失函数， N 表示训练样本的个数； Ω(f) 称为正则项（或者惩罚项），表示模型的复杂程度； λ 是系数，用于权衡经验风险与模型复杂程度。 λ 的取值，正是机器学习中，我们需要调节的参数。
   结构风险最小化（structural risk minimization）：模型不仅能够比较优秀的拟合训练样本，而且能够具备比较优秀的泛化能力。表示如下：

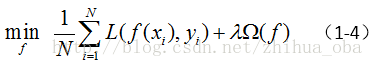
  李航《统计学习方法》中指出： 结构风险最小化等价于正则化。

二、正则项：L0范数、L1范数、L2范数
  结构风险最小化（正则化）中， Ω(f) 称为正则项（regularizer），或者惩罚项（penalty term），表示模型的复杂程度。正则项一般是模型复杂程度的单调递增函数，模型越复杂，正则项的值越大。 Lp 范数是常用的正则项，也就是说，正则项通常是模型参数向量的范数。接下来我们详细介绍 L0 范数、 L1 范数、 L2 范数。
  1、L0范数
  L0范数：描述向量中非0元素的个数。
  L0范数可以实现模型参数向量的稀疏。但是，L0范数的优化求解是NP-hard问题，因此难以应用。
  补充知识点：实现模型参数向量的稀疏有什么好处呢？主要有以下两点：进行特征选择、提高模型可解释性。

  2、L1范数
  L1范数：描述向量中各个元素的绝对值之和。
  L1范数可以实现模型参数向量的稀疏。L1范数是L0范数的最优凸近似。不同于L0范数的优化求解是NP-hard问题，L1范数的优化求解相对容易。
  补充知识点：L1范数为什么能够实现模型参数向量的稀疏呢？
  例如，最简单的线性回归模型：

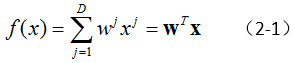
  这里假设，我们采用的损失函数为平方损失（square loss）。则前文中提到的结构风险最小化（公式1-4），可以表示为：

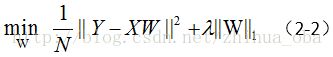
  从凸优化的角度来讲，上式（2-2）等价于

其中 C 是与 λ 对应的常数。
  现在，为了方便可视化，我们假设（2-1）中 D=2 ，也就是数据对象只含有两个属性。那么在 (w1,w2) 平面上，可以画出目标函数的等高线，如下图1中彩色圈圈；而约束条件则变成该平面上，半径为 C 的一个norm ball，我们称其为 L1 -ball，如下图1黑线菱形中的区域。 等高线与 L1 -ball首次相交的地方就是最优解。
  注意：在二维空间上，最优解的地方，就有 w1=0 ；如果更高维的空间上，可以想象最优解的地方，将会产生更多的稀疏。

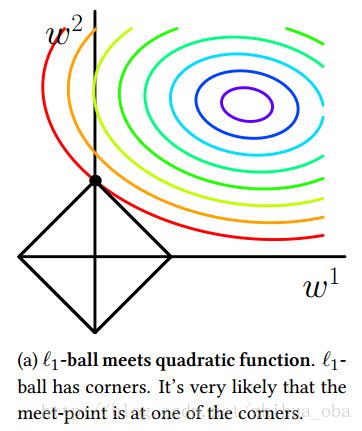
图1
  关于L1范数为什么能够实现模型参数向量的稀疏，更多的知识以及证明，可以参考文章 《Sparsity and Some Basics of L1 Regularization》。

  3、L2范数
  L2范数：描述向量中各元素的平方之和，然后求平方根。
  补充知识点：L2范数不能实现模型参数向量的稀疏。
  例如，最简单的线性回归模型：

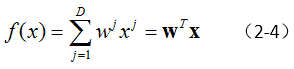
  这里假设，我们采用的损失函数为平方损失（square loss）。则前文中提到的结构风险最小化（公式1-4），可以表示为：

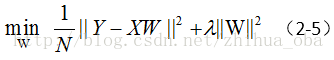
  从凸优化的角度来讲，上式（2-5）等价于

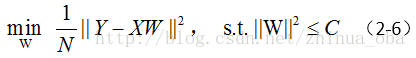
其中 C 是与 λ 对应的常数。
  现在，为了方便可视化，我们假设（2-4）中 D=2 ，也就是数据对象只含有两个属性。那么在 (w1,w2) 平面上，可以画出目标函数的等高线，如下图2中彩色圈圈；而约束条件则变成该平面上，半径为 C 的一个norm ball，我们称其为 L2 -ball，如下图2黑线圈圈中的区域。 等高线与 L2 -ball首次相交的地方就是最优解。
  注意：与L1范数（图1中）不同的是，在二维空间上，最优解的地方， w1 趋近于0，而不是等于0；如果更高维的空间上，可以想象最优解的地方，将会有更多的参数 w1 趋近于0，而不是等于0。因此，L2范数不能实现模型参数向量的稀疏。
  由于L2范数不能实现模型参数向量的稀疏，因此得到的参数 w 仍然需要数据对象的所有属性才能计算预测结果，因此从计算量上来说并没有得到改观。

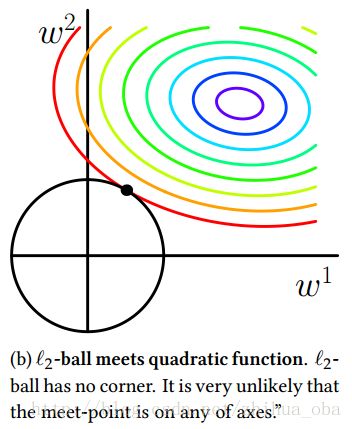
图2
   补充知识点：L2范数有助于处理条件数（condition number）不好的情况下矩阵求逆很困难的问题。
  关于这个知识点，感兴趣的童鞋可以阅读文章 《机器学习中的范数规则化之（一）L0、L1与L2范数》。

三、关于L1正则化与L2正则化的问题整理
  1、从贝叶斯的角度来看，正则化等价于对模型参数引入先验分布：对参数引入高斯先验分布等价于L2正则化，对参数引入拉普拉斯分布等价于L1正则化。详细内容，可以参考文章《Regularized Regression: A Bayesian point of view》。
  2、L1正则化问题的求解，可以使用近端梯度下降（Proximal Gradient Descent，简称PGD）、坐标轴下降、最小角回归法；L2正则化问题的求解，可以使用梯度下降（随机梯度下降、批量梯度下降）、牛顿法、拟牛顿法等等。
  3、关于L1范数与L2范数的求导，可以参考《常用范数求导》。
  4、L1范数会选择少量的特征，其他的特征都是0；L2范数会选择更多的特征，这些特征都会趋近于0。Lasso在特征选择的时候非常有用，而Ridge就只是一种规则化而已。如果在所有特征中，只有少数特征起主要作用的情况下，那么选择Lasso比较合适，因为它能自动选择特征；如果在所有特征中，大部分特征都能起作用，而且起的作用很平均，那么使用Ridge也许更合适。如果模型的特征非常多，我们希望一些不重要特征的系数归零，从而让模型的系数稀疏化，那么选择L1正则化。如果我们需要相对精确的多元逻辑回归模型，那么L1正则化可能就不合适了。在调参时，如果我们目的仅仅是为了解决过拟合问题，一般选择L2正则化就可以；但是，如果选择L2正则化之后，发现还是存在过拟合的问题，就可以考虑L1正则化。