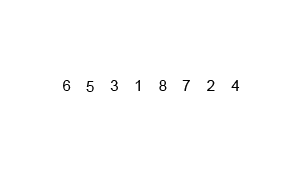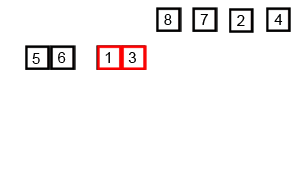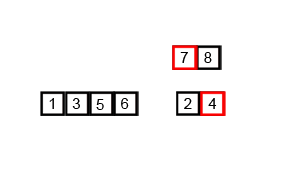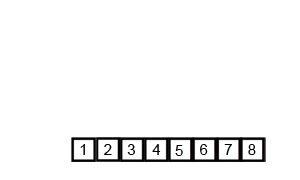【C++】八大排序算法 ：GIF + 亲测代码 +专项练习平台

主要目的呢，是为了我自己记住。
这篇写完，以前那几篇排序的博客都可以删了。
五天之后就设为粉丝可见啦。

1、八大排序总览

• 比较类排序：通过比较来决定元素间的相对次序，由于其时间复杂度不能突破O(nlogn)，因此也称为非线性时间比较类排序。

• 非比较类排序：不通过比较来决定元素间的相对次序，它可以突破基于比较排序的时间下界，以线性时间运行，因此也称为线性时间非比较类排序。

代码实现一律放到文末，方便有兴趣边看边练的小伙伴动手自己写。

2、冒泡排序

不啰嗦，直接上图：

相邻两个数两两相比，n[i]跟n[j+1]比，如果n[i]>n[j+1]，则将两个数进行交换

复杂度分析：
在一般情况下，每一个数都要与之后的数进行匹配，所以匹配次数将与数据量n挂钩，又由于每轮匹配都要进行(n-1)次比较，所以平均时间复杂度为O(n^2)。

当然，可以对冒泡排序进行优化，比方说可以设置一个标志位，当哪次匹配没有发生数据交换时，就不用再进行后面的匹配了。
还可以做个优化，纪录下数据尾部已经稳定下的部分，比如说倒数八个数字已经稳定，那么匹配到倒数第九个数，只要和倒八匹配一下即可知道要不要往后继续匹配。

不过，冒泡排序一般也不会用在大数排序上，所以嘛，老老实实的把基础代码写好比较重要。

3、快速排序

快速排序，我觉得这篇写的很nice：通俗点聊聊算法 - 快速排序（亲测代码示例）

大数排序，至少也要用快速排序。

4、插入排序

这个动画已经够明确了吧。

复杂度分析

时间复杂度：插入算法，就是保证前面的序列是有序的，只需要把当前数插入前面的某一个位置即可。
所以如果数组本来就是有序的，则数组的最好情况下时间复杂度为O（n）。
如果数组恰好是倒=倒序，比如原始数组是5 4 3 2 1，想要排成从小到大，则每一趟前面的数都要往后移，一共要执行n-1 + n-2 + … + 2 + 1 = n * (n-1) / 2 = 0.5 * n2 - 0.5 * n次，去掉低次幂及系数，所以最坏情况下时间复杂度为O（n2）

平均时间复杂度(n+n2 )/2，所以平均时间复杂度为O（n2）

空间复杂度：插入排序算法，只需要两个变量暂存当前数，以及下标，与n的大小无关，所以空间复杂度为：O（1）

5、希尔排序

希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个文件恰被分成一组，算法便终止。

这个步长可以好好考虑一下要设多大，一般取三分之一表长就好了。

复杂度分析

1. 时间复杂度：最坏情况下，每两个数都要比较并交换一次，则最坏情况下的时间复杂度为O（n2）, 最好情况下，数组是有序的，不需要交换，只需要比较，则最好情况下的时间复杂度为O（n）。

经大量人研究，希尔排序的平均时间复杂度为O（n^1.3）（这个我也不知道咋来的，书上和博客上都这样说，也没找到个具体的依据）。

2. 空间复杂度：希尔排序，只需要一个变量用于两数交换，与n的大小无关，所以空间复杂度为：O（1）。

6、选择排序

1. 第一个跟后面的所有数相比，如果小于（或小于）第一个数的时候，暂存较小数的下标，第一趟结束后，将第一个数，与暂存的那个最小数进行交换，第一个数就是最小（或最大的数）
2. 下标移到第二位，第二个数跟后面的所有数相比，一趟下来，确定第二小（或第二大）的数
   重复以上步骤
   直到指针移到倒数第二位，确定倒数第二小（或倒数第二大）的数，那么最后一位也就确定了，排序完成。

复杂度分析

1. 不管原始数组是否有序，时间复杂度都是O（n^2），
   因为没一个数都要与其他数比较一次，（n-1）2次，分解：n^2-2n+1, 去掉低次幂和常数，
   剩下n^2,
   所以最后的时间复杂度是n^2

2. 空间复杂度是O（1）,因为只定义了两个辅助变量，与n的大小无关，所以空间复杂度为O（1）

7、堆排序

其实这个我也没看太懂。。
我觉得还不如直接构造成二叉搜索树，然后前序遍历。

堆排序的基本思想是：将待排序序列构造成一个大顶堆，此时，整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换，此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆，这样会得到n个元素的次小值。如此反复执行，便能得到一个有序序列了

复杂度分析

1. 时间复杂度：堆排序是一种选择排序，整体主要由构建初始堆+交换堆顶元素和末尾元素并重建堆两部分组成。其中构建初始堆经推导复杂度为O(n)，在交换并重建堆的过程中，需交换n-1次，而重建堆的过程中，根据完全二叉树的性质，[log2(n-1),log2(n-2)…1]逐步递减，近似为nlogn。所以堆排序时间复杂度最好和最坏情况下都是O(nlogn)级。

2. 空间复杂度：堆排序不要任何辅助数组，只需要一个辅助变量，所占空间是常数与n无关，所以空间复杂度为O(1)。

8、归并排序

1. 时间复杂度：递归算法的时间复杂度公式：T[n] = aT[n/b] + f(n)

无论原始数组是否是有序的，都要递归分隔并向上归并排序，所以时间复杂度始终是O（nlog2n）

2. 空间复杂度：

每次两个数组进行归并排序的时候，都会利用一个长度为n的数组作为辅助数组用于保存合并序列，所以空间复杂度为O（n）

9、基数排序

这个图也挺有趣啊。

1. 时间复杂度：
   每一次关键字的桶分配都需要O(n)的时间复杂度，而且分配之后得到新的关键字序列又需要O(n)的时间复杂度。

假如待排数据可以分为d个关键字，则基数排序的时间复杂度将是O(d*2n) ，当然d要远远小于n，因此基本上还是线性级别的。

系数2可以省略，且无论数组是否有序，都需要从个位排到最大位数，所以时间复杂度始终为O(d*n) 。其中，n是数组长度，d是最大位数。

2. 空间复杂度：
   　　基数排序的空间复杂度为O(n+k)，其中k为桶的数量，需要分配n个数。

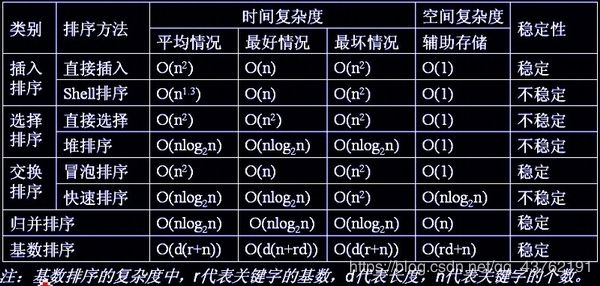
各算法复杂度

---

冒泡排序代码实现

#include
#include

using namespace std;

void bulu(vector<int>& vec) {
	int sz = vec.size();
	if (sz == 0)
		return;
	int temp = 0;
	int continue_flag = 1;

	while (continue_flag) {
		for (int i = 0, j = 1; j < sz; i++, j++) {

			continue_flag = 0;

			if (vec[i] > vec[j]) {
				temp = vec[i];
				vec[i] = vec[j];
				vec[j] = temp;
				continue_flag = 1;
			}
		}
	}
}

int main()
{
	vector<int> test = { 2,5,1,5,3,7,5,7,5,6 };
	bulu(test);
	for (int i = 0; i < 10; i++) {
		cout << test[i] << " ";
	}
	return 0;
}

快速排序代码实现

见上面那篇博文推荐

插入排序代码实现

#include
#include

using namespace std;

//交换数组元素位置位置
void swap(int& a, int& b)
{
	int temp = a;
	a = b;
	b = temp;
}

/*
插入排序。注意，若后面一个元素比其前面一个元素小，则将这两个元素交换位置，然后再来比较这个插入元素与前面一个元素的大小，若小，则还需要交换这两个元素位置，一直到这个插入元素在正确的位置为止
*/
void insertSort(int a[], int length)
{
	for (int i = 1; i < length; i++)
	{
		for (int j = i - 1; j >= 0 && a[j + 1] < a[j]; j--)
		{
			swap(a[j], a[j + 1]);
		}
	}

}

int main()
{
	int a[] = { 2,1,4,5,3,8,7,9,0,6 };

	insertSort(a, 10);

	for (int i = 0; i < 10; i++)
	{
		cout << a[i] << " ";

	}
	cout << endl;
	system("pause");
	return 0;

}

希尔排序代码实现

int shellSort(int* shell,int ishell)
{
	int step,i,temp;
	step = ishell/3+1;	//	设定步长
	for( ; step>0 ;)
	{
		for(i=0 ; i+step<ishell ; )
		{
			if(shell[i] > shell[i+step])
			{
				temp = shell[i];
				shell[i] = shell[i+step];
				shell[i+step] = temp;
			}
			i++;
		}
		step--;
	}
}

选择排序代码实现

void SelectSort(int* select,int lenth)
{
	int i,j,temp,min;
	for(i = 0;i<lenth;i++)
	{
		min = i;
		for(j = i+1;j<lenth;j++)
		{
			if(select[i]>select[j])
			{
				min = j;
			}
		}
		if(min != i)
		{
			temp = select[i];
			select[i] = select[min];
			select[min] = temp;
		}
	}
}

归并排序

#include
using namespace std;

void merge(int arr[], int L, int R, int M)
{
	int LEFT_SIZE = M - L;
	int  RIGHT_SIZE = R - M + 1;

	int* L_arr = new int [LEFT_SIZE];
	int* R_arr = new int[RIGHT_SIZE];

	
	int i,j,k;
	//将左边数组的值赋值给新数组
	for (i = L; i < M; i++)
	{
		L_arr[i - L] = arr[i];
	}
	
	//将右边数组的值赋值给新数组
	for (i = M; i <= R; i++)
	{
		R_arr[i - M] = arr[i];
	}

	i = 0, j = 0, k = L;
	//左右数组同时比较
	while (i < LEFT_SIZE && j < RIGHT_SIZE)
	{
		if (L_arr[i] < R_arr[j])
		{
			arr[k] = L_arr[i];
			i++;
			k++;

		}
		else
		{
			arr[k] = R_arr[j];
			j++;
			k++;
		}
	}

	while (i < LEFT_SIZE)
	{
		arr[k] = L_arr[i];
		i++;
		k++;
	}
	while (j < RIGHT_SIZE)
	{
		arr[k] = R_arr[j];
		j++;
		k++;
	}
}

void mergeSort(int arr[], int L, int R)
 {
	if (L == R)
	{
		return;
	}
	int M = (L + R) / 2;
	mergeSort(arr, L, M);
	mergeSort(arr, M+1, R);
	merge(arr, L,R,M+1);

}

int main()
{
	int arr[] = { 2,8,23,10,4,1,6,7 };
	int L = 0;
	int R = 7;
	int M = 4;
	//merge(arr, L, R, M);
	mergeSort(arr, L, R);

	for (int i = 0; i <= R; i++)
	{
		cout << arr[i] << endl;
	}

	return 0;
}

基数排序

 
/*算法：基数排序*/
 
#include 
using namespace std;

bool rxsort(int A[],int l,int h,int d,int k){
    if(NULL==A||l>h)
        return false;
    int size = h-l+1;
 
    int* counts = new int[k];//用于计数排序的辅助数据，详见计数排序
    int* temp = new int[size];//用于存储重新排序的数组
    int index;
    int pval=1;
    //依次处理不同的位
    for(int i=0;i<d;i++){
        //counts数组清零
        for(int j=0;j<k;j++)
            counts[j] = 0;
 
        for(int j=l;j<=h;j++){
            /*
            1.data[j]/pval：去掉数字data[j]的后i个数，例如：
            当data[j]=1234,i=2时，此时pval=100,data[j]/pval=12;
            2.(data[j]/pval)%k：取数字data[j]/pval的最后一位数
            3.(int)(data[j]/pval)%k:取数字data[j]的第i位数
            */
            index = (int)(A[j]/pval)%k;
            /*
            统计数组A中每个数字的第i位数中各个数字的频数,用于计数排序；
            */
            counts[index]++;
        }
        //计算累加频数，用户计数排序
        for(int j=1;j<k;j++)
            counts[j] = counts[j] + counts[j-1];
        //使用倒数第i+1位数对A进行排序
        for(int j=h;j>=l;j--){
            index = (int)(A[j]/pval)%k;
            temp[counts[index]-1] = A[j];
            counts[index]--;
        }
        //将按第i为数排序后的结果保存回数组A中
        for(int j=0;j<size;j++)
            A[j+l] = temp[j];
        //更新pval
        pval = pval*k;
    }
    delete[] counts;
    delete[] temp;
}
 
int main(){
    int A[] = {712,303,4,18,89,999,70,26};
    rxsort(A,0,7,3,10);
    for(int i=0;i<8;i++)
        cout<<A[i]<<" ";
}

练习平台

CSDN提供排序算法练习平台

如果上面那个网站进不去，可以去LeetCode或者牛客嘛