机器学习笔记-Blending and Bagging

集成学习系列：

• Blending and Bagging
• Adaptive Boosting
• Decision Tree
• Random Forest
• Gradient Boosted Decision Tree

Blending and Bagging

1 - 为什么要用aggregation

如果我们已经有了一些模型 hypothesis h y p o t h e s i s ，或者已经有了一些 feature f e a t u r e ，这些 hypothesis h y p o t h e s i s 可以帮助我们做预测，我们怎么样将这些已有的 hypothesis h y p o t h e s i s 或者是有有预测性的 feature f e a t u r e 结合起来，让它们在一起的时候可以work的更好。这样的模型我们称之为 aggregation model a g g r e g a t i o n   m o d e l ，也就是融合起来的模型。本篇介绍在 aggregation a g g r e g a t i o n 中非常典型的两个做法， blending b l e n d i n g 和 bagging b a g g i n g 。

那么为什么要用 aggregation a g g r e g a t i o n 呢？

1.1 - 一个关于aggregation的故事

假如你有15个朋友，这15个朋友都告诉你明天股市的涨跌预测，那么你在听取了这15个朋友的预测之后，如何决定呢？

• select from usual performance s e l e c t   f r o m   u s u a l   p e r f o r m a n c e
  从他们的平常的表现中选择最厉害的那个人，听取他的意见作为最后的决策依据，这也就是我们以前学过的 validation v a l i d a t i o n 的方法，
• mix uniformly m i x   u n i f o r m l y
  但是如果只听一个人的，白白浪费了其余人的判断力，浪费了资源。所以另一种方式是以每人一票的方式，让这15个朋友进行投票，综合他们的判断做出最后的结果，
• mix non m i x   n o n - uniformly u n i f o r m l y
  但是考虑到可能每一个人的能力确实不尽相同，所以可以选择另外一种投票的方式：可以信赖的人给多一点的票数，不是那么可以信赖的人的票数可以少一点。
• combine conditionally c o m b i n e   c o n d i t i o n a l l y
  又或者是可以根据具体的情况来进行选择， 例如这些朋友中有些人擅长分析科技类的股票，有些人擅长传统产业的股票，那么在不同的情况下，就选择听取不同的人的意见。
• ⋯ ⋯

我们想要将这15个人的意见融合起来的事情， 就是 aggregation a g g r e g a t i o n 想要做的事情，将每个人的预测结果融合起来以达到最好的结果。

我们将上述的这个问题用数学的形式表示出来：每一个朋友就代表每一个 hypothesis h y p o t h e s i s ： g1,g2,⋯,gT g 1 , g 2 , ⋯ , g T ，也就是说这样就一共有15个预测模型。

• select from usual performance s e l e c t   f r o m   u s u a l   p e r f o r m a n c e
  
  G(x)=gt∗ with t∗=argmint∈1,2,⋯,T Eval(g−t) G ( x ) = g t ∗   w i t h   t ∗ = a r g m i n t ∈ 1 , 2 , ⋯ , T   E v a l ( g t − )
• mix uniformly m i x   u n i f o r m l y
  
  G(x)=sign(∑t=1T1⋅gt(x)) G ( x ) = s i g n ( ∑ t = 1 T 1 ⋅ g t ( x ) )
• mix non m i x   n o n - uniformly u n i f o r m l y
  
  G(x)=sign(∑t=1T αt⋅gt(x)) with αt≥0 G ( x ) = s i g n ( ∑ t = 1 T   α t ⋅ g t ( x ) )   w i t h   α t ≥ 0
  
  通过参数 α α 给每一个 gt g t 不同的权重。这种情况是包括前两种情况的：
  
  • 当 αt=|[Eval(gt) smallest]| α t = | [ E v a l ( g t )   s m a l l e s t ] | 的时候，是第一种情况。（其中 1=|[◯]|,if ◯ 1 = | [ ◯ ] | , i f   ◯ 成立； 0=|[◯]|,if ◯ 0 = | [ ◯ ] | , i f   ◯ 不成立）
  • 当 αt=1 α t = 1 的时候，是第二种情况。
• combine conditionally c o m b i n e   c o n d i t i o n a l l y
  
  G(x)=sign(∑t=1Tqt(x)⋅gt(x)) with qt(x)≥0 G ( x ) = s i g n ( ∑ t = 1 T q t ( x ) ⋅ g t ( x ) )   w i t h   q t ( x ) ≥ 0
  
  权重的参数不再是 α α ，而是变成了和输入特征 x x 相关的函数 qt(x) q t ( x ) 。
  
  • 当 qt(x)=αt q t ( x ) = α t 的时候，就是以上的第三种情形。

1.2 - Selection by Validation

G(x)=gt∗ with t∗=argmint∈1,2,⋯,T Eval(g−t) G ( x ) = g t ∗   w i t h   t ∗ = a r g m i n t ∈ 1 , 2 , ⋯ , T ⁡   E v a l ( g t − )

考虑上述提出的最简单的第一种情形，利用 Validation V a l i d a t i o n 来选择最好的 gt g t 。这个方法的优点是简单。但是该方法中有一个重要的假设，如果最终想要得到一个比较好的 gt∗ g t ∗ ，那么首先在得到的一堆 g−t g t − 中至少要有一个不错的， 或者说是 strong s t r o n g 的。如果你的所有的朋友都对股市其实只是一知半解，那么你最终得到的最好的那一个人的意见也不见得会好到那里去。
而这里我们重点要谈论的 aggregation a g g r e g a t i o n 不是这样的。 aggregation a g g r e g a t i o n 擅长做的事情是，在没有一个很强的 hypothesis h y p o t h e s i s 的时候，或者说有一堆比较弱弱的但是还勉强的 hypothesis h y p o t h e s i s 的时候，把他们融合起来，通过集体的智慧，可以使得他们变的很强。这篇会讲解具体的不同的 aggregation a g g r e g a t i o n 的做法。

1.3 - 为什么Aggregation可以work的很好呢

为什么 aggregation a g g r e g a t i o n 可以很好的 work w o r k 呢，讨论如下的一个二分类的问题，假设我们只可以使用垂直的线和水平的线对上述的 data d a t a 进行分类(这样的话模型的复杂度很低)，那么只用一条分割线无论如何都是不能完全划分的。但是如果可以将不同的垂直的线和水平的线结合起来对数据进行划分呢(这里垂直的线和水平的线就是不同的 hypothesis h y p o t h e s i s )，可能就可以得到比较好的结果。如下是结合了三条线对数据进行了划分。

从以上的结果可以看出来，如果只有一些弱弱的 hypothsis h y p o t h s i s ，即那些只能是垂直或者是水平的线，但是如果将他们通过一定的方式合并起来的话，可能就会得到比较好的结果， 这里例子中就是得到了一个比较复杂的分类边界。这可能说明 aggregation a g g r e g a t i o n 拓展了 model m o d e l 的复杂度，这样看来 aggregation a g g r e g a t i o n 的作用就好像是 feature transform f e a t u r e   t r a n s f o r m 一样。

另一个对 aggregation a g g r e g a t i o n 可以 work w o r k 的不错的解释是，当使用 PLA P L A 算法对如下的 data d a t a 进行划分的时候，会得到不同的分割线，其中的每一个都能将数据完美的分开，但是我们知道如果通过 SVM S V M 的话，可以得到有 large l a r g e - margin m a r g i n 的分隔超平面。而使用 PLA P L A 得到的可能就是图中灰色的任意一条，但是通过 aggregation a g g r e g a t i o n ，或者说所有的这些灰色的线投票之后，就会得到一条比较 largin margin l a r g i n   m a r g i n 的线，在这种情况下 aggregation a g g r e g a t i o n 就会有 large margin l a r g e   m a r g i n 的类似于 regularization r e g u l a r i z a t i o n 的效果。

以前我们的认识是， feature transform f e a t u r e   t r a n s f o r m 和 regularization r e g u l a r i z a t i o n 是在做相反的事情，前者就像在踩油门，后者像是在踩刹车。而在做 aggregation a g g r e g a t i o n 的时候，好像同时在做这两件事情：可能是 feature transform f e a t u r e   t r a n s f o r m ，使得 model m o d e l 更加的 powerful p o w e r f u l ；也可能是 regularization r e g u l a r i z a t i o n ，在帮助模型做一个比较适中的选择。 所以如果可以把 aggregation a g g r e g a t i o n 做好的话，可能就同时将 feature transform f e a t u r e   t r a n s f o r m 和 regularization r e g u l a r i z a t i o n 做好了。

2 - Uniform Blending

上面比较直观的讲解了 aggregation a g g r e g a t i o n 的好处，接下来我们开始讲解应该怎么样来做 aggregation a g g r e g a t i o n ，即怎么样把这些 hypothesis h y p o t h e s i s 融合起来。
我们可以使用 blending b l e n d i n g 的方法来做 aggregation a g g r e g a t i o n ， blending b l e n d i n g 这种方法主要用在我们已经收集到了一堆 hypothesis h y p o t h e s i s ，即已经有了一些已知的模型，需要对它们进行融合的情形。

如果对所有的 hypothesis h y p o t h e s i s 一视同仁，即给每一个 g(x) g ( x ) 相同的权重来进行组合的话，这种方式成为 uniform blending。 u n i f o r m   b l e n d i n g 。

2.1 - Uniform Blending用于分类

对于二元分类 binary classification b i n a r y   c l a s s i f i c a t i o n 来说， uniform blending u n i f o r m   b l e n d i n g 给每一个 hypothesis h y p o t h e s i s 相同的权重（所以叫 uniform u n i f o r m ）来进行融合。根据融合的结果给出最终的判断，如下：

G(x)=sign(∑t=1T 1⋅gt(x)) G ( x ) = s i g n ( ∑ t = 1 T   1 ⋅ g t ( x ) )

• 如果所有已知的 g(x) g ( x ) 是相同的，那么 aggregation a g g r e g a t i o n 是没有效果的
• 如果所有已知的 g(x) g ( x ) 差距很大，多数的意见会纠正少数的意见。例如在以下的问题中，共有三个 g(x) g ( x ) ：两个垂直线，一个水平线。对于数据点1和2来说，有两条线说它们是 ∘ ∘ （左边的垂直线和水平线），一条线（右边的的垂直线）说它们是 × × ，所以它们被划分为 ∘ ∘ 。对于其他的数据点来说也是使用这样的规则来进行划分的。
  
• 如果是多分类问题：那么我们就需要统计数据点在每一个类别上的“得票数”，将得票数最多的为该数据点的类别。
  G(x)=argmax1≤k≤K∑t=1T|[gt(x)=k]| G ( x ) = a r g m a x 1 ≤ k ≤ K ⁡ ∑ t = 1 T | [ g t ( x ) = k ] |

2.2 - Uniform Blending用于回归

uniform blending u n i f o r m   b l e n d i n g 将所有回归的值取平均：

G(x)=1T∑t=1Tgt(x) G ( x ) = 1 T ∑ t = 1 T g t ( x )

• 如果所有已知的 g(x) g ( x ) 是相同的，那么 aggregation a g g r e g a t i o n 是没有效果的
• 如果所有已知的 g(x) g ( x ) 差距很大，那么对于一个数据点来说，有些 g(x) g ( x ) 可能低估了， 有些 g(x) g ( x ) 可能高估了，这样的话，它们的平均值就可能会估计的更准确一下。

小结： 如果 aggregation a g g r e g a t i o n 这样的方法想要 work w o r k 的很好的话，有一个很重要的前提是 g(x) g ( x ) 要有一定的多样性 diverse d i v e r s e 。当 g(x) g ( x ) 有一定的多样性的时候，即使只是做很简单的融合的操作，例如说 uniform blending u n i f o r m   b l e n d i n g ，也会有很好的结果。

2.3 - Uniform Blending的理论分析

针对 uniform blending u n i f o r m   b l e n d i n g 用于 regression r e g r e s s i o n ，我们可以做简单的理论分析来解释为什么通过这样的 aggregation a g g r e g a t i o n 的方式可以得到比单个的 hypothesis h y p o t h e s i s 更好的结果。
uniform blending u n i f o r m   b l e n d i n g 用于 regression r e g r e s s i o n 的一般方式是：

G(x)=1T∑t=1Tgt(x) G ( x ) = 1 T ∑ t = 1 T g t ( x )

如果只是针对特定的 x x ，那么上式可以写作：

G=1T∑t=1Tgt G = 1 T ∑ t = 1 T g t

接下来我们想要分析的问题是： 1T∑((gt−f)2)=avg(gt−f)2 1 T ∑ ( ( g t − f ) 2 ) = a v g ( g t − f ) 2 和 (G−f)2 ( G − f ) 2 的大小关系，前者表示的是所有 g g 在 x x 上的平均错误，也可以理解为任选一个 g g 在 x x 上的平均错误；后者是经过 aggregation a g g r e g a t i o n 得到的 G G 在 x x 上的平均错误。
即比较 g g 的平均错误（因为取到哪个都是不一定的）和 G G 的错误的大小关系。

avg ((gt−f)2)=avg(g2t−2gtf+f2)=avg(g2t)−2Gf+f2=avg(g2t)−G2+(G−f)2=avg(g2t)−2G2+G2+(G−f)2=avg(g2t−2gtG+G2)+(G−f)2=avg((gt−G)2)+(G−f)2(7)(8)(9)(10)(11)(12) (7) a v g   ( ( g t − f ) 2 ) = a v g ( g t 2 − 2 g t f + f 2 ) (8) = a v g ( g t 2 ) − 2 G f + f 2 (9) = a v g ( g t 2 ) − G 2 + ( G − f ) 2 (10) = a v g ( g t 2 ) − 2 G 2 + G 2 + ( G − f ) 2 (11) = a v g ( g t 2 − 2 g t G + G 2 ) + ( G − f ) 2 (12) = a v g ( ( g t − G ) 2 ) + ( G − f ) 2

当对所有的 x x 进行计算的时候，可以得到如下的等式：

avg(Eout(gt))=avg(ε(gt−G)2)+Eout(G) a v g ( E o u t ( g t ) ) = a v g ( ε ( g t − G ) 2 ) + E o u t ( G )

所以可以得到的是：

avg(Eout(gt))≥Eout(G) a v g ( E o u t ( g t ) ) ≥ E o u t ( G )

也就是说在使用 uniform blending u n i f o r m   b l e n d i n g 这样的 aggregation a g g r e g a t i o n 做 regression r e g r e s s i o n 的时候，得到的结果 G G 确实要比所有 g g 的平均表现好。尽管不知道是不是比最好的那个 g g 表现好。

2.4 - variance，bias

偏差 bias b i a s 度量了学习算法的期望预测和真实结果之间的偏离程度，即刻画了学习算法本身的拟合能力；
方差 variance v a r i a n c e 度量了同样大小的训练集的变动所导致的学习性能的变化，刻画了数据的扰动所造成的影响。

假设在每一轮的学习中，由N笔资料训练得到 gt g t ，共进行T轮的学习，每一轮使用来自同一分布的不同的资料。假设T可以取到无穷多，则得到：

g¯=limT→∞G=limT→∞1T∑t=1Tgt=εD A(D) g ¯ = l i m T → ∞ ⁡ G = l i m T → ∞ ⁡ 1 T ∑ t = 1 T g t = ε D ⁡   A ( D )

avg(Eout(gt))=avg(ε(gt−g¯)2)+Eout(g¯) a v g ( E o u t ( g t ) ) = a v g ( ε ( g t − g ¯ ) 2 ) + E o u t ( g ¯ )

avg(Eout(gt)) a v g ( E o u t ( g t ) ) 代表的是学习算法 A A 表现的期望； Eout E o u t 称为 bias b i a s ，也就是学习算法的期望预测和真实结果之间的偏离程度； avg(ε(gt−g¯)2) a v g ( ε ( g t − g ¯ ) 2 ) 称为方差 variance v a r i a n c e ，不知道为什么要写一个 ε ε ，西瓜书上是没有的。
所以一个学习算法的表现可以拆分为两项，这个学习算法产生的共识和每一个 gt g t 和这个共识的差异。

这块和西瓜书上写的有点不符合：日后补充
E(f,D)=bias2(x)+var(x)+ε2 E ( f , D ) = b i a s 2 ( x ) + v a r ( x ) + ε 2 (西瓜书)

所以通过这样的 aggregation a g g r e g a t i o n 的方式，可以看到降低了 variance v a r i a n c e ，使得最终的学习算法的表现变好。

3 - Linear and Any Blending

linear blending l i n e a r   b l e n d i n g 是要给每一个 gt g t 不同的权重（票数） αt α t ，模型如下所示：

G(x)=sign(∑t=1Tαt⋅gt(x)) with αt≥0 G ( x ) = s i g n ( ∑ t = 1 T α t ⋅ g t ( x ) )   w i t h   α t ≥ 0

那么现在的问题就是要求解这些参数 αt α t ，求解的方法就是最小化 Ein E i n 。
如果我们现在要做的是 Regression R e g r e s s i o n 问题的话，我们求解 α α 的策略当然就是最小化 square error s q u a r e   e r r o r 。

Linear blending for regression

minαt≥0Ein(α)=minαt≥01N∑n=1N(yn−∑t=1Tαtgt(xn))2 m i n α t ≥ 0 ⁡ E i n ( α ) = m i n α t ≥ 0 ⁡ 1 N ∑ n = 1 N ( y n − ∑ t = 1 T α t g t ( x n ) ) 2

如果将 (g1,g2,⋯,gT) ( g 1 , g 2 , ⋯ , g T ) 看做是 xn x n 的特征转化 Φ Φ ，那么以上的问题就可以变为我们熟悉的带有特征转换的线性模型，如下（1）所示，只不过是多了一个条件。并且这个过程和 probability SVM p r o b a b i l i t y   S V M 中的 two level learning t w o   l e v e l   l e a r n i n g 的方法很相像：第一步将 SVM S V M 用作一个特征的转换，然后使用 logReg l o g R e g 做微调。

linear regression + transformation

minwi≥01N∑n=1N(yn−∑i=1d~wiϕi(xn))(1) (1) m i n w i ≥ 0 ⁡ 1 N ∑ n = 1 N ( y n − ∑ i = 1 d ~ w i ϕ i ( x n ) )

所以我们可以说： linear blending l i n e a r   b l e n d i n g 就等于一个将许多的 hypothesis h y p o t h e s i s 当成一个特征转化的线性模型，外加一个限制条件。即：
linear blending=linar model+hypothesis as transform+constraints。 l i n e a r   b l e n d i n g = l i n a r   m o d e l + h y p o t h e s i s   a s   t r a n s f o r m + c o n s t r a i n t s 。

minαi≥01N∑n=1Nerr(yn，∑t=1Tαtgt(xn)) m i n α i ≥ 0 ⁡ 1 N ∑ n = 1 N e r r ( y n ， ∑ t = 1 T α t g t ( x n ) )

这个问题的求解不同于以往的仅仅是多了个 constraints c o n s t r a i n t s 。对于 binary classification b i n a r y   c l a s s i f i c a t i o n 问题来说，如果在求解之后发现 αt<0 α t < 0 ，那么说明学习算法觉得这个 αt α t 对应的 gt g t 反过来用能更好的 fitting f i t t i n g 数据。所以在实际操作中通常都不考虑 αt>0 α t > 0 这个条件限制。

所以 linear blending l i n e a r   b l e n d i n g 的解法就是加了 feature transform f e a t u r e   t r a n s f o r m 的 linear model l i n e a r   m o d e l 的解法，其中的 linear model l i n e a r   m o d e l 可以是线性回归，或者是逻辑斯蒂回归。

现在我们来关注一下一个基本的问题：那些 gt g t 是怎么产生的？通常这些 gt g t 是在各自不同的 model m o d e l 下最小化 Ein E i n 得到的。
所以如果在做 selection s e l e c t i o n （见本篇第一节， aggregation a g g r e g a t i o n 的第一种方式）的时候，如果是根据 Ein E i n 来做选择的话，模型的复杂度就会更大（是不是可以理解为越复杂的模型越容易被选到，因为它可以拟合的很好，做到 Ein E i n 很小），所以我们通常会用 Evalidation E v a l i d a t i o n 来做选择。
同样的，如果我们使用 Ein E i n 作为最小化的目标来做 linear aggregation l i n e a r   a g g r e g a t i o n ，会导致更大的模型的复杂度，更加容易导致过拟合。也就是说，在实际应用中通常不使用 Ein E i n 来学习 α α ，因为这样很容易 overfitting o v e r f i t t i n g ，而是在 Dval D v a l 上训练 α α 使得 Eval E v a l 最小。并且在 Dtrain D t r a i n 上得到一些 g− g − ，

3.1 - Linear Blending

Linear Blending L i n e a r   B l e n d i n g

1. 将数据分为 train data t r a i n   d a t a 和 validation data v a l i d a t i o n   d a t a
2. 从 Dtrain D t r a i n 得到 g−1,g−2,⋯,g−T g 1 − , g 2 − , ⋯ , g T −
3. 将 Dval D v a l 中的数据 (xn,yn) ( x n , y n ) 利用 g−1,g−2,⋯,g−T g 1 − , g 2 − , ⋯ , g T − 这些“特征转换”变换为 (zn=Φ−(xn),yn) ( z n = Φ − ( x n ) , y n ) ，其中 Φ−(x)=(g−1(x),⋯,g−T(x)) Φ − ( x ) = ( g 1 − ( x ) , ⋯ , g T − ( x ) )
4. 利用线性模型求解资料 {(zn,yn)} { ( z n , y n ) } 上的 α α ， α=Lin({(zn,yn)}) α = L i n ( { ( z n , y n ) } )
5. 返回最后的结果 GLinB(x)=Lin(innerprob(α,Φ(x))) G L i n B ( x ) = L i n ( i n n e r p r o b ( α , Φ ( x ) ) ) ，

需要注意的是， Φ(x)=(g1(x),⋯,gT(x)) Φ ( x ) = ( g 1 ( x ) , ⋯ , g T ( x ) )

3.2 - Any Blending

在第4步中，我们也可以考虑不使用线性模型，而是使用非线性的模型 (nonlinear SVM) ( n o n l i n e a r   S V M ) ，这样的方式称为Any Blending或者Stacking。

Any Blending A n y   B l e n d i n g

1. 将数据分为 train data t r a i n   d a t a 和 validation data v a l i d a t i o n   d a t a
2. 从 Dtrain D t r a i n 得到 g−1,g−2,⋯,g−T g 1 − , g 2 − , ⋯ , g T −
3. 将 Dval D v a l 中的数据 (xn,yn) ( x n , y n ) 利用 g−1,g−2,⋯,g−T g 1 − , g 2 − , ⋯ , g T − 这些“特征转换”变换为 (zn=Φ−(xn),yn) ( z n = Φ − ( x n ) , y n ) ，其中 Φ−(x)=(g−1(x),⋯,g−T(x)) Φ − ( x ) = ( g 1 − ( x ) , ⋯ , g T − ( x ) )
4. g=Any({(zn,yn)}) g = A n y ( { ( z n , y n ) } )
5. 返回 GanyB=g(Φ(x)) G a n y B = g ( Φ ( x ) )

这样模型会更加的 powerful p o w e r f u l ，但是同时也更加容易 overfitting o v e r f i t t i n g 。所以 any blending a n y   b l e n d i n g 要非常的小心， 要加 regularization r e g u l a r i z a t i o n 等等。

4 - Bagging (Bootstrap Aggregation)

如果已经通过某些方法得到了很多的 g g ，我们可以通过 blending b l e n d i n g 的方式将它们融合起来，使得最后的分类器表现的很好。如果每一个 g g 的权重（票数）是相同的， 那么可以得到 uniform blending u n i f o r m   b l e n d i n g 的 aggregation a g g r e g a t i o n 方式；如果权重不是相同的， 那么就得到了 linear blending l i n e a r   b l e n d i n g ；如果想要得到更为复杂的模型，在考虑在不同的模型下使用不同的权重的话，可以使用 stacking s t a c k i n g 来做。

这里有有一个很关键和很基础的问题是，这些 g g 是怎么来的呢，我们是不是可以一边学习 g g ，一边对它们进行融合。这是我们接下来要谈论的问题。因为 aggregation a g g r e g a t i o n 在 g g 非常的 diverse d i v e r s e 的时候会做的很好，所以我们就考虑怎么样可以得到不一样的 g g 呢？

• 不同的模型可能会得到不同的 g g
• 对于用一个模型，不同的参数可能会得到不同的模型：例如对于 GD G D 算法来说，当 η=0.001,0.01,0.1⋯10 η = 0.001 , 0.01 , 0.1 ⋯ 10 的时候会得到不同的模型。
• 不同的初始值可能会得到不同的模型，例如 PLA P L A 算法
• 资料的不同可以得到不同的模型，例如当在做 cross validation c r o s s   v a l i d a t i o n 的时候，不用的几份数据可能会得到不同的 g g 。

接下来我们使用的方式是使用同一份资料来制作不用的 g g （不同于 cross validation c r o s s   v a l i d a t i o n 只能得到不同的 g− g − ），利用的工具称为 bootstrapping b o o t s t r a p p i n g ，它的作用是从手上已有的资料来模拟一些不一样的资料。

4.1 - Bootstrapping Aggregation

bootstrapping：从原有的 N N 笔资料中做 N N 次有放回的采样（ sampling with replacement s a m p l i n g   w i t h   r e p l a c e m e n t ）。既然是有放回的，那么就可能存在原资料中的某一笔被采样到了多次，或者一次都没有被采样到的情形。通过 bootstrapping b o o t s t r a p p i n g 这样的方式得到的资料记为 D~t D ~ t 。

bagging（bootstrap aggregation） b a g g i n g （ b o o t s t r a p   a g g r e g a t i o n ）

1. 通过 bootstrapping b o o t s t r a p p i n g 的方式抽取大小为 N′ N ′ 的资料 D~t D ~ t
2. 从资料 D~t D ~ t 利用算法 A A 中得到不同的 gt g t
3. 对 gt g t 做融合 G(x)=Uniform({gt}) G ( x ) = U n i f o r m ( { g t } )

这样的方法我们称为 bootstrap aggregation b o o t s t r a p   a g g r e g a t i o n ， 一般我们称之为 BAGging B A G g i n g 。我们把底层的算法 A A 称为 base algorithm b a s e   a l g o r i t h m ，建筑在其上的演算法称为 meta algorithm m e t a   a l g o r i t h m 。

Bagging B a g g i n g 通过利用 bootstrap b o o t s t r a p 这样的机制生出一系列的 g g ， 然后使用 uniform u n i f o r m 的方式进行 aggregation a g g r e g a t i o n 。

4.2 - Bagging Pocket的表现

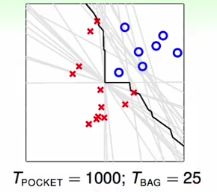
由于 pocket p o c k e t 算法对于不同的资料表现会有很不同，如下图中的灰色的线是使用 pocket p o c k e t 算法在利用 boostrap b o o s t r a p 机制得到的25组不同的资料上得到的25条不同的线。通过将这些线进行融合得到了一个非线性的边界，如图中黑色的线所示。

如果算法 base algorithm b a s e   a l g o r i t h m A