Faiss向量召回引擎如何做到快速查找最近邻

欢迎来我的小站转转~~

背景

Faiss是Facebook开源的向量召回引擎，用于寻找与某个向量最相似的N个向量。

Faiss第一次release发布于2018.02.23，但其作者Matthijs在加入Facebook之前的2011年就已经发表了一篇关于最近邻搜索的论文，Faiss就是基于此论文思想实现的。读懂了这篇论文，Faiss的索引方式就清楚了。

问题描述

给定D维向量$x$和集合$\Gamma =y_1,y_2\dots y_N$ ,需要找到与$x$距离最短的k个最近邻。

以欧氏距离为例，可表示为：

$$L=k-argmi{n}_{i=0:N}||x-y_i||$$

在我们的应用中，$x\in \Gamma$

问题规模

我们试着以最粗暴的方法进行穷举搜索，来看一下这个解的复杂度有多高。

1. 构造距离矩阵：每两个向量$x$与$y$的距离计算公式为$\sqrt{\Sigma (x_i-y_i{)}^2},i\in [1,D]$ ，耗费时间为 $O(D)$ , 距离矩阵包含 $N^2$ 个元素，总共耗时为 $O(D\ast N^2)$
2. 从距离矩阵中查找到k个最近邻，若用最小堆算法，时间复杂度为$O((N-k)logk)$

取$N=2000W,k=1000,D=1000$

得到

• 距离矩阵包含400T个元素，假设每个距离为float占用32bit，至少占用1600TB空间
• 构造距离矩阵运算时间复杂度数量级为$10^{17}$
• 从距离矩阵中找到k个最近邻的时间复杂度数量级为$10^9$

最近邻离线表

一般来说向量集合都是每天更新的，这时候可以试着直接把每个向量对应的k个最近邻保存起来

1. 构造距离矩阵+N个k近邻查找耗时为 $O(D{N}^2+N\ast (N-k)\ast logk)$
2. 构造最近邻离线表空间占用 $N\ast k$

在我们的场景中得到

1. 找到N个k近邻查找的耗时数量级为 $10^{17}$
2. 存储空间为 $1600TB$ (构造后删除)+320G(假设每个索引用int表示，分数用float表示)

查找k最近邻的耗时: O(1)

向量量化(Vector Quantization)

在我们的场景中，其实不需要最精确的距离，允许一定程度的误差。在这种情况下，我们可以引入向量量化方法，将向量的数量大幅度缩小。

所谓向量量化，就是将原来无限的空间 $R^D$ 映射到一个有限的向量集合 $\mathcal{C}=\{c_i,i\in [1,l]\}$ 中，其中 $l$ 是一个自然数。将这个从 $R^D$ 到集合 $\mathcal{C}$ 的函数记为 $q$ ，则 $\forall q(y)\in \mathcal{C}$，在信息论中称 $\mathcal{C}$ 为codebook。

当然这里的映射函数也不是随便指定的，需要满足误差最小的原则，一种方法是将优化函数设置为最小平方误差$MSE(q)={\mathbb{E}}_X[d(q(y),y{)}^2]$

咦，正好就是k-means方法的目标函数！因此我们可以用k-means作为寻找最佳codebook的方法。

那现在我们来分析一下进行向量量化占用的空间和时间复杂度

假设我们将原来2000W个向量映射到大小为20W的集合中(平均每个中心点代表100个向量，已经引入了较大的误差)

1. 距离矩阵：只需要存储对应$\mathcal{C}$ 中向量之间的距离，占用的空间为$||\mathcal{C}|{|}^2$，此例中为$400G\times 4B=1.6T$
2. $y\to c\in \mathcal{C}$的映射关系，若以int标识一个向量，则共约$N\times 4=80M$内存
3. 时间复杂度：k-means算法的时间复杂度为$O(m_{iter}NkD)$，其中$m_{iter}$为迭代次数，N为原空间向量数量，k为中心点数量，D为向量维度。在此例中时间复杂度为$4m\ast 10^{15}$，取迭代次数为25就已经达到了暴力搜索的数量级，只要迭代次数稍微上升些，时间复杂度还会更高。

乘积量化PQ(Product Quantization)

很多时候我们向量不同部分之间的分布是不同的

那么就可以将向量分成$m$个不同的部分，对每个部分进行向量量化,假设平均划分，则每个部分的维度大小为$D^{\ast }=D/m$

一个向量 $[x_1,x_2,\dots ,x_{D^{\ast }},\dots ,x_{D-D^{\ast }+1},\dots ,x_D]$ ，可以划分为m组向量$[x_{i\_1},x_{i\_2},\dots ,x_{i\_D^{\ast }}]$，每组的codebook为${\mathcal{C}}_i$，对应的量化器记为$q_i$，$\forall q_i(x_{i\ast })\in {\mathcal{C}}_i$。则最终的全局codebook就是 $\mathcal{C}={\mathcal{C}}_1\ast {\mathcal{C}}_2...\ast {\mathcal{C}}_m$，乘积量化的名称也来源于此。

以m=4为例，要达到上一节的20W量级，$||{\mathcal{C}}_i||$只需要达到22即可，要恢复到2000W级别也只需要达到67即可。

以 $\mathcal{C}$ 达到2000W量级的情况为例，每个分组的codebook中心点数量$k^{\ast }$为67，现在来分析下对应的空间和时间复杂度

1. 中心点之间的距离矩阵: 记$||{\mathcal{C}}_i||$ 为 $k^{\ast }$ ，距离矩阵大小为 $O(m\ast (k^{\ast }{)}^2)$ 。若用float表示距离，此例子中距离矩阵约为70M
2. $y\to c\in {\mathcal{C}}_i$的映射关系，若以int标识一个向量，则共约 $m\times N\times 4=320M$内存
3. 聚类时间复杂度：k-means算法的时间复杂度依然为$O(m_{iter}NkD)$，在此例中需要对m组分别进行k-means，总时间复杂度为$O(mN{k}^{\ast }D\ast m_{iter})$，此例中为$5m\ast 10^{12}$，比上例降低了3个数量级
4. 距离矩阵时间复杂度：维度D与距离矩阵元素数量的乘积，即 $O(Dm(k^{\ast }{)}^2)$，约$7\times 10^{10}$

乘积量化大幅度降低空间占用的本质原因就在于：表达的向量空间是 $(k^{\ast }{)}^m$，但占用的磁盘空间为$m{k}^{\ast }$

论文中给出的经验取值是 $k^{\ast }=256$ ，$m=8$ ，对应的向量空间大小为$2^{64}$约$1.8\times 10^{19}$

Quantization场景下的距离计算

在没有Quantization的场景下，距离计算是直接对两个点计算$||x-y|{|}_2$

但在Quantization的场景下，不需要直接计算x和y的距离，而是通过中心点进行计算。这种方式有两个变种：

SDC

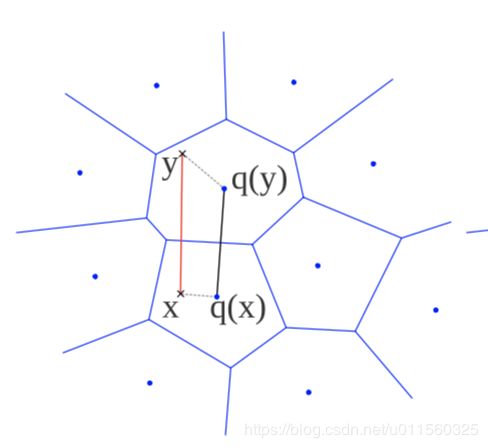
SDC(Symmetric Distance Computation): 两个向量之间的距离以两个向量所在的中心点距离来度量。误差小于等于x到中心点的距离+y到中心点的距离。

在PQ场景下，SDC距离表示为：$SDC(x,y)=\hat{d}(x,y)=d(q(x),q(y))=\sqrt{{\Sigma }_{j}d(q_j(x),q_j(y){)}^2}$

由于中心向量之间的距离已经存好(见上一节)，计算x与y之间的距离只要查表即可，表的规模约70M，计算距离矩阵耗时数量级$10^{10}$

如果不想占用距离矩阵的空间，则时间复杂度为$O(Dm{k}^{\ast })$，约为$10^5$

ADC

ADC(Asymmetric Distance Computation):x与y之间的距离以x与y所在的中心点距离来度量。用到三角形性质：两边之差小于第三边，所以误差一定小于等于y与中心点之间的距离

在PQ场景下，ADC距离表示为：$\tilde{d}(x,y)=d(x,q(y))$

记向量x的第i组元素为$u_i(x)$，则$ADC(x,y)=\sqrt{{\Sigma }_{j}d(u_j(x),q_j(y){)}^2}$

此场景下如果想要通过查表得到距离，则数据准备环节的距离矩阵的大小约为 $O(mn{k}^{\ast })\ast 4=20G$ (每个向量都要和m个分组中每个中心向量计算距离)，耗时数量级 $10^{13}$

若直接计算，则复杂度与不查表版本的SDC相同，也是$O(Dm{k}^{\ast })$，约为$10^5$

若使用查表策略，则ADC在精度更高的情况下，付出了更多的内存代价

IVFADC

上一节中，直接计算的时间主要耗费在与所有的中心向量进行对比上了。一种很自然的方法就是先找到一个大概的候选中心节点，避免与大量根本不可能的是最近邻的点进行计算。

粗糙量化(coarse quantization)+残差量化

因此，Matthijs在论文中提出了粗糙量化+残差量化的过程。具体来说，就是先从整个数据集合中构造一个大小为$k{k}^{{}^{\prime }}$ (假设取值为1000)的小规模codebook ${\mathcal{C}}_c$，量化器记为$q_c$，于是每个向量都会有一个残差$r(y)=y-q_c(y)$。原始的向量可能会有特别大的分布差异/不平衡，但通过残差化之后的结果可以大幅度缓解这种问题。

再对$r(y)$使用PQ步骤，由于 $r(y)$ 相对于原始向量的"能量"更低，所以通过PQ步骤可以更精确地进行模拟。记PQ步骤的量化器为 $q_p$，则 y 通过 $q_c(y)+q_p(y-q_c(y))$ 来表示。这样的话两个向量x、y之间的距离 $d(x,y)$ 可以近似表示为

$$\ddot{d}(x,y)=d(x,q_c(y)+q_p(y-q_c(y)))=d(x-q_c(y),q_p(y-q_c(y)))=\sqrt{{\Sigma }_{j}d(u_j(x-q_c(y)),q_{p_j}(u_j(y-q_c(y))){)}^2}$$

记残差量化的codebook大小为$k_p$ (以64为例)，如果要将这里的 $u_j(x-q_c(y))$ 提前计算好，即对每个x提前计算好与所有中心向量 $c\in {\mathcal{C}}_c$ 的距离，时间复杂度为$O(DNk{k}^{{}^{\prime }})$，本文例子为$10^{13}$ ，空间复杂度为$O(Nk{k}^{{}^{\prime }})$ ，本文的例子为20G*4B=80GB。

索引结构

通过倒排索引，能大幅提高搜索效率

论文中提出使用 $k{k}^{{}^{\prime }}$ 个倒排索引存储粗糙中心点 $c_i$对应的向量列表 ${\mathcal{L}}_i$ 。每个向量通过如下的格式表示，其中id是向量的索引id，code是对应的PQ中心点索引列表。PQ中每个组的中心点数量为$k^{\ast }$，则需要 $\lceil lo{g}_2{k}^{\ast }\rceil$ 个bit来表示哪一个中心点，共 $m\ast \lceil lo{g}_2{k}^{\ast }\rceil$个bit

当进行搜索时，可以通过 $q_c$ 函数获取对应簇下所有的向量

索引过程

1. 通过量化器 $q_c$ 将向量 $y$ 映射到 $q_c(y)$
2. 计算残差 $r(y)=y-q_c(y)$
3. 将残差 $r(y)$ 量化到 $q_p(r(y))$ ，其中包含了m个分组
4. 构造一个 $id|code$ 的 entry 并加入到 $q_c(y)$ 对应的倒排列表 $\mathcal{L}$

搜索过程

由于很多情况下，最近邻不一定当前的簇里，所以不仅要查找当前簇，还要查找邻近的簇。

1. 计算 ${\mathcal{C}}_c$ 中与入参x最近的 $w$ 个中心点, $O((kk-w)\ast logw)$
2. 如果还有中心点没处理，取出一个中心点 $c_i$ ，并计算对应的 $r(x)=q_p(x-c_i)$。否则跳到步骤6
3. 计算 $r(x)$ 与各个分组内的中心点距离，$O(m\ast \frac{D}{m}\ast k^{\ast })=O(D{k}^{\ast })$
4. 由于同一个倒排索引中对应的 $q_c(x)$ 与 $q_c(y)$ 是相同的，所以 x 与 y 的距离只要看残差距离 $d(r(x),r(y))$ 。由于 $r(x)$ 与各个中心点的距离都已经计算好，所以每个向量只需要查表m次即可。O(m)
5. 返回步骤2
6. 使用最小堆得到K个距离最小的向量，由于每个倒排索引预期元素数量为$\frac{N}{k{k}^{{}^{\prime }}}$，所以耗时$O((\frac{N}{k{k}^{{}^{\prime }}}-K)\ast logK)$

整个搜索过程的耗时为: $O((k{k}^{{}^{\prime }}-w)\ast logw)+w\ast (O(D{k}^{\ast })+O(m))+O((\frac{N}{k{k}^{{}^{\prime }}}-K)\ast logK)$

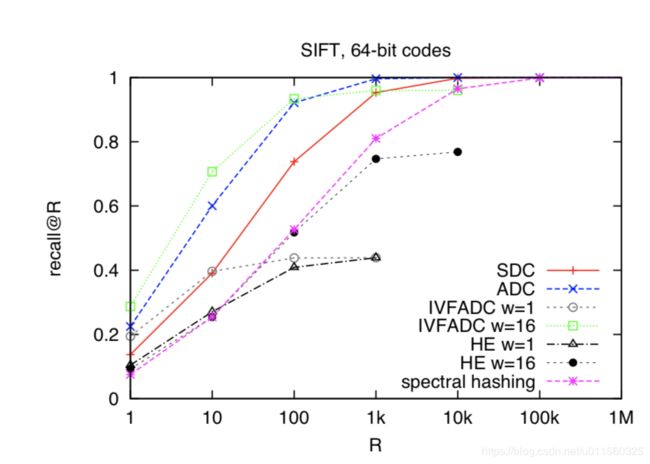
实验效果

优化

1. 残差量化中，不同的向量到各自中心的残差都放在一起进行量化了，其实隐含了不同聚类中的分布相同的假设。这个假设带来了一定误差，但不这么做的话内存占用就要扩大 $k{k}^{{}^{\prime }}$ 倍了
2. 对向量的不同分组方式会导致表现有很大的差异。论文中的实验显示，比起随机分组，相关的字段应该放在同一个分组在某些场景下可以使正确率提高2-3倍。在索引之前，可以通过一些相似度分析的方法将向量通过合适的顺序进行组织。
3. $w$ 如果选取为1，会导致只查找当前簇内的向量，带来的结果可能比SDC还要差很多。作者在论文中的建议是取 $w=8$，但不同的场景下还是应该先进行测试以取得内存空间与耗时的平衡。

总结

Faiss 本质上是将向量编码为有限个向量的组合，将向量之间的距离计算转换为可提前计算的有限个向量之间的距离。

简化计算的关键：

1. 候选向量缩小到邻域向量
2. 乘积量化带来的表达能力跃升： $ka\ll (a{)}^k$
3. 预先计算乘积量化结果的距离矩阵，使距离计算变为查表操作。(乘积量化使距离矩阵的空间需求在可忍受的范围内)

举个例子：
如下向量12、13

首先对他们进行粗糙聚类计算

发现他们的聚类id都是1

接着分成三组计算残差

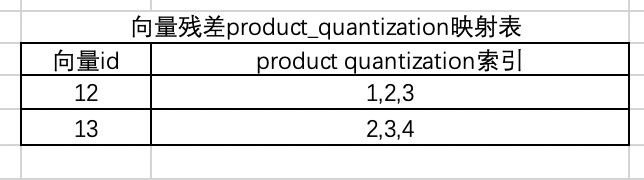
对残差进行乘积量化

那么向量12、13的距离就可以直接通过累加三组乘积量化vector距离得到，其中vector距离都是提前计算好的

$d(12,13)=\sqrt{(a_{12}{)}^2+(b_{23}{)}^2+(c_{34}{)}^2}$

参考文献:
《Product Quantization for Nearest Neighbor Search》: https://lear.inrialpes.fr/pubs/2011/JDS11/jegou_searching_with_quantization.pdf