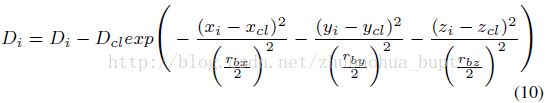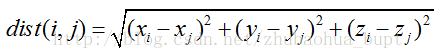转载请说明出处:
http://blog.csdn.net/zhubaohua_bupt/article/details/70194047
基于密度的点云聚类算法可以识别三维点云物体,也可以对三维点云去噪处理。
本文研究了两种基于密度的点云聚类方法,先简单介绍一下两种算法,后面会详细的介绍算法原理以及效果。
第一种方法叫做密度减法聚类
功能:能识别特定尺寸的点云簇集合,通过参数设置期望形状的大小。
输入:一片点云
输出:是几个聚类完成的点簇和聚类中心点
类别不需要提前设定,最终聚成几类由初始参数决定。
论文 3D Candidate Selection Method for Pedestrian Detection on Non-Planar Roads 用其来提取行人的ROI。
第二种方法叫做自适应密度聚类
功能:可以寻找出每个点云的三维连通域,不需要设置形状和大小参数。
输入:一片点云
输出:每个点云所在的连通域以及此点云集合一共有多少连通域。
类别不需要提前设定,最终聚成几类由连通规则中参数决定。
论文 一种聚类与滤波融合的点云去噪平滑方法 和 密度聚类算法在连续分布点云去噪中的应用 用这种聚类方法来对点云去噪。
下面来分别详细介绍一下两种方法。
一:第一种方法 密度减法聚类
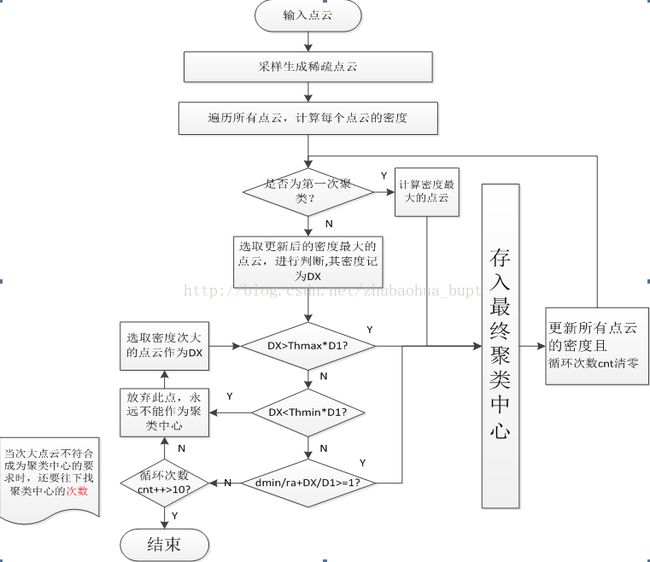
先看一下流程,这里说明一下,为了提高速度,我们在聚类的时候没有直接对稠密的处理,而是先采样生产稀疏点云,旨在提速。
1 此方法对密度定义为
公式9中rax,ray和raz就是那个你想要设置的聚类形状参数。可以看出
<1> 对于一个特定的三维点,离其越近的点对它的密度加成越大。
<2>从求和符号可以看出,它是遍历所有三维点。
2 再看公式(10),这个公式是这个算法的核心。
Di表示检测出的一定聚类中心和一定不是聚类中心的其他三维点的密度,xi,yi,zi为其坐标,rbx,rby,rbz为用于跟更新Di密度的半径参数。Dcl为上一次聚类中心的密度。xcl,ycl,zcl为其坐标。
为什么要搞这么一个公式呢?
因为聚类的目的是想得到几个密度比较大的点簇,是为了避免多个聚类中心集中在一起。举个例子,你面前有几个人而且你有他们的点云,你想通过聚类把这几个人分出来,他们体型相差很大比如,这些人中有人身宽体胖的人,有人身材比较瘦小,你的本意是想把这几个人都识别出来。回到算法中,看流程图,如果我们每此检测下一次聚类中心的时候去掉了更新所有点云这一步骤,那么那个胖的人身上一定会被聚类成好多个聚类中心。
说白了,公式10起到这样一个作用:凡是离上次刚得到的聚类中心近的点,它们的密度都会被削减,削减影响的范围由rbx,rby,rbz控制。rb参数的选取一般要大于ra参数,论文中取rbm=1.5ram m=x,y,z;
3 最终聚类点簇的大小差异控制
这部分参数也是本方法的一个重要的参数,因为它们控制着最终聚类结果中每个点簇的大小,以及最大点簇和最小点簇的密度差异有多大。
具体参数有:Thmax,Thmin,ra,cnt和公式9中的半径参数。
其中,公式中的半径参数控制着聚类物体的大概三维尺寸(椭球)
Thmax:当一个候选聚类中心的密度大于第一个聚类中心密度的Thmax倍,直接就接纳此聚类中心。
Thmin:当一个候选聚类中心的密度小于第一个聚类中心密度的Thmin倍,直接把对应三维点拉黑,以后再也不用,并认为它不会是聚类中心。
ra:此参数控制相邻聚类中心的距离,选取的越大,生成的聚类中心间隔越大。
最后,流程图还剩一个参数dmin,这个参数的含义是:本候选聚类中心到其他聚类中心距离中的最小值。
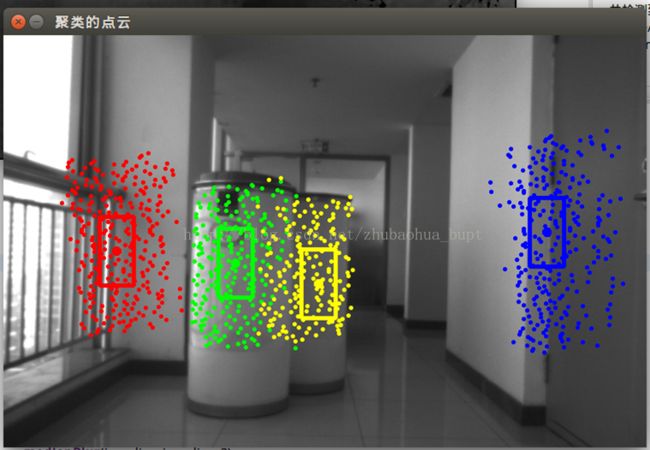
原理部分就说这么多,下面来看一下效果,我暂用它来检测一个桶:参数设置好后,效果如下(当然,这种方法还是有缺陷的,即只能检测形状,其他和桶三维大小差不多的物体也会被检测出来):
图2 输入: 选取的一定高度的稀疏点云(上方也会有几个,是因为我们点云数据不太准确,会有一些噪点)
图3 聚类输出(不同颜色表示不同点簇,聚类中心用大圆点表示)
第二种:自适应密度聚类
这种方法就是实际上就是三维连通域检测。聚类最后的输出是若干块三维连通域。和上一种方法不一样,这种聚类方法不需要设置新装参数,输出的每块连通域的大小不一定相等。下面给出这种 方法的流程图:
图 4 自适应密度聚类算法流程
此算法寻找连通域的步骤对应于流程图的第二至第三个判断条件组成的循环体。每循环一次,生成一个新的三维连通域。
密度定义 :此方法没有对密度定义,而是定义了一个类似密度的核心对象:是在点云空间范围内,如果离点p的欧式距离小于e的其他点云数大于一个值Minpts,就认为点p是核心对象。
那么为什么称这种方法叫自适应密度聚类呢?
答案是,聚类它可以根据点云自适应求出半径参数e和点数Minpts,不需要自己提前设定,当然自己也可以提前设定。
怎么求参数e和Minpts呢?
引用原文的话:
在上述密度聚类步骤中,初始半径e 和最小邻域数MinPts均为自定义参数。参数初始值设置好后,需要根据聚类效果不断调整这两个参数以获得最好的聚类效果,比较耗时。为了解决这一问题,本文提出一种自适应参数计算方法。
首先,根据式(1) 计算任意两点之间的欧式距离1。
然后根据式( 2)-式( 3) 求得dist(i,j ) 的最大值maxdist 和最小值mindist,maxdist = Max{dist( i,j)| 0 ≤ i < n,0 ≤ j < n} ( 2)
mindist = Min{dist( i,j )| 0 ≤ i < n,0 ≤ j < n} ( 3)
进而根据式( 4) 求得距离间隔distrange。
distrange = maxdist -mindist ( 4)
其中,n 表示点的数目。将距离间隔等距分为十段,统计dist(i,j)在每段范围内的频数,初始半径e 的值即为erang 所在分段的中值。erang 的计算公式如式( 5)所示。
erang = Max{pk | 0 ≤ k < 10} (5)
初始半径e 确定后,根据e 逐步增大最小邻域数目MinPts,计算邻域超过最小邻域数目的点的数目pNum(计算公式如式( 7)所示) 。随着最小邻域数目的增加,pNum 会逐渐减少并趋于稳定,选择拐点所在的最小邻域数目作为MinPts。其中,对于任意给定点p 的邻域点数目pNumi的计算如式( 6)所示。
pNumi = count{dist( i,j)< e | 0 ≤ j < n} ( 6)
那么:
pNum = count{ pNumi ≥ MinPts |0 ≤ i < n} ( 7)
通过该方法可以实现初始半径和最小邻域数的自动选择,进而避免这两个参数的反复设置。
下面给出这种方法的效果:
测试说明:
输入:用深度相机获得的半稠密点云,如图3
输出:聚类结果图,如图4,图5,去噪图,如图6。
图 5带有噪声的点云图
图6 聚类结果图(所有的核心对象,颜色不同,所属类别不同)
图7 聚类结果图(聚类后的非核心对象密度小,认为是噪声)
图8 点云经过聚类去噪图
可以看出,这种去噪方法还不错,缺点是计算量较大,实时性难以满足。i7-6700的笔记本上一秒3帧左右。