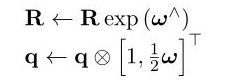VIO-第1章 概述与课程介绍

VIO-第1章 概述与课程介绍

内容总结

内容：

IMU原理与模型
后端优化与VIO BA
滑动窗口算法与FEJ
后端求解系统与代码
前端介绍
VIO初始化
VIO系统回顾

预备知识汇总：

数学：线性代数、微积分、概率论
编程：Linux、C++、OpenCV
英语：文献阅读
专业知识：2D/3D 计算机视觉、图像处理

VIO 概述

1.VIO：

以视觉与IMU融合实现的里程计

IMU：惯性测量单元

组成：陀螺仪和加速度计，共6轴。

较高频率（>100Hz），易受自身温度、零偏、振动等因素干扰，积分得到的平移与旋转容易漂移。

视觉：

较低频率（15-60Hz居多），通过相机特整点进行匹配，推断相机运动。

2.种传感器比较：

3.两种融合方案

紧耦合：直接将图像的特征匹配点与IMU定位，进行融合。典型方案为MSCKF和非线性优化。
松耦合：将IMU定位与视觉定位，直接进行融合。后处理方式输出。典型方案为卡尔曼滤波器。
紧耦合优势：视觉BA中含有IMU信息，整体层面最优。而且，可以对所有运动、测量信息进行建模，达到最优。

4.主要总结：

IMU数据的状态信息，及噪声
对含有IMU测量信息和视觉特征点信息的非线性优化
随时间将如何变化

预备知识

1.三维刚体运动（2种）：

李代数与李群
四元数

2.两种导数（具体推导请自行查看《SLAM十四讲》）：

以上2种导数更新方式，误差相差不大。证明代码如下：

#include 
#include 
using namespace std; 

#include 
#include 

#include "sophus/so3.h"
#include "sophus/se3.h"

int main( int argc, char** argv )
{
    // 沿Z轴转90度的旋转矩阵
    Eigen::Matrix3d R = Eigen::AngleAxisd(M_PI/2, Eigen::Vector3d(0,0,1)).toRotationMatrix();
    
    
    // 四元数乘法饶动微元
    Eigen::Matrix<double,4,1> w_q ;

    w_q << 0.005,0.01,0.015,1;


    // 李树饶动微元
    Eigen::Vector3d w;
    
    w << 0.01,0.02,0.03;


    // 生成李树与四元数
    Sophus::SO3 SO3_R(R);               // Sophus::SO(3)可以直接
    Eigen::Quaterniond q(R);            // 或者四元数

    cout<<"\n***********准备开始*******************\n"<<endl;

    cout<<endl;
    cout<<"R : \n"<<R<<endl;

    cout<<"******************************"<<endl;

    cout<<endl;
    cout<<"SO(3) from matrix: \n"<<SO3_R<<endl;

    cout<<endl;
    cout<<"q : \n"<<q.coeffs()<<endl;

    cout<<"************我是分割线*****************\n\n\n"<<endl;

    // 计算饶动后的数值
    Sophus::SO3 SO3_updated_R_left  = Sophus::SO3::exp(w)*SO3_R;
    Sophus::SO3 SO3_updated_R_right = SO3_R*Sophus::SO3::exp(w);
    

    cout<<"***********R饶动的值（李树）**********"<<endl;
    cout<<"**********R饶动的值（左）*********"<<endl;

    cout<<"SO3 updated = \n"<<SO3_updated_R_left<<endl;

    cout<<"**********R饶动的值（右）*********"<<endl;

    cout<<"SO3 updated = \n"<<SO3_updated_R_right<<endl;

    cout<<"***************************************\n\n\n"<<endl;
    
    /********************萌萌的分割线*****************************/
    cout<<"************我是分割线*****************"<<endl;
    
    //计算四元数的值
    Eigen::Quaterniond w_q_0(w_q);
    Eigen::Quaterniond q_updated_left;
    Eigen::Quaterniond q_updated_right;

    q_updated_left  = w_q_0 * q;
    q_updated_right = q * w_q_0;

    q_updated_left.normalize();
    q_updated_right.normalize();

    cout<<"***********四元数饶动的值*********\n"<<endl;
    cout<<"***四元数饶动的值（微变量）*******"<<endl;

    cout<<"w_q = \n"<<w_q_0.coeffs()<<endl;

    cout<<"\n***四元数饶动的值（结果zuo）******"<<endl;

    cout<<"q_updated = \n"<<q_updated_left.coeffs() <<endl;

    cout<<"***四元数饶动的值（结果you）*********"<<endl;

    cout<<"q_updated = \n"<<q_updated_right.coeffs()<<endl;

    cout<<"***************************************\n\n\n"<<endl;
    
    //传结果
    cout<<"************我是分割线*****************"<<endl;

    cout<<"***********jie        guo*********\n"<<endl;

    cout<<"***************************************"<<endl;

    cout<<"李树上（左） = \n"<<SO3_updated_R_left<<endl;

    cout<<"***************************************"<<endl;

    cout<<"李树上（右） = \n"<<SO3_updated_R_right<<endl;


    Sophus::SO3 SO3_q_l(q_updated_left );
    Sophus::SO3 SO3_q_r(q_updated_right);


    cout<<"\n***四元数饶动的值（结果zuo）******"<<endl;

    cout<<"q_左 = \n"<<SO3_q_l<<endl;

    cout<<"***四元数饶动的值（结果you）*********"<<endl;

    cout<<"q_右 = \n"<<SO3_q_r<<endl;

    cout<<"***************************************\n\n\n"<<endl;


    return 0;
}

并请在CMakeList.txt添加,下面代码：

在这里插入代码片


cmake_minimum_required( VERSION 2.8 )
project( useSophus )

# 为使用 sophus，您需要使用find_package命令找到它
find_package( Sophus REQUIRED )
include_directories( ${Sophus_INCLUDE_DIRS} )

add_executable( useSophus useSophus.cpp )
target_link_libraries( useSophus ${Sophus_LIBRARIES} )

以上是在cmake下，进行运行。具体自行查看cmake操作，后续会上传至，GitHub上。或，自行学习。

运行结果：