深度学习总的正则化、半监督学习、多任务学习以及Bagging
正则化的定义为"对学习算法的修改–旨在减少泛化误差而非训练误差"。正则化的策略包括参数范数惩罚、约束范数惩罚、提前终止以及Dropout等等。
一、参数范数惩罚
参数惩罚是指在目标函数 J J J中添加一个参数范数惩罚 Ω ( θ ) \Omega(\theta) Ω(θ),限制模型的学习能力：
J ~ ( θ ; X , y ) = J ( θ ; X , y ) + α Ω ( θ ) \tilde{J}(\theta;X, y)=J(\theta; X, y)+\alpha\Omega(\theta) J~(θ;X,y)=J(θ;X,y)+αΩ(θ)
当我们的算法最小化正则化后的目标函数 J ~ \tilde{J} J~时，它会降低原始目标 J J J关于训练数据的误差并同时减少在某些衡量标注下参数 θ \theta θ的规模。选择不同的参数范数 Ω \Omega Ω会偏好不同的解。
参数范数惩罚通常只惩罚权重 W W W，不管b。因为(1)精确拟合偏置所需的数据比拟合权重少的多，每个权重会指定两个变量如何相互作用，我们需要在各种条件下观察这两个变量才能良好地拟合权重，而每个偏置只控制一个单变量。这意味着我们不对其进行正则化也不会导致太大的方差。(2)正则化偏置参数可能会导致明显的欠拟合。基于以上两点，我们通常指惩罚权重 W W W，即 θ = ( W ; b ) ≈ ( W ) \theta =(W;b)\approx (W) θ=(W;b)≈(W)。
1. L2参数正则化: Ω ( θ ) = 1 2 ∣ ∣ w ∣ ∣ 2 \Omega(\theta)=\frac{1}{2}||w||^2 Ω(θ)=21∣∣w∣∣2
目标函数：
J ~ ( w ; X , y ) = J ( w ; X , y ) + α 2 w T w \tilde{J}(w;X,y)=J(w;X,y)+\frac{\alpha}{2}w^Tw J~(w;X,y)=J(w;X,y)+2αwTw
计算梯度：
▽ w J ~ ( w ; X , y ) = ▽ w J ( w ; X , y ) + α w \bigtriangledown _w\tilde{J}(w;X,y)=\bigtriangledown_wJ(w;X,y)+\alpha w ▽wJ~(w;X,y)=▽wJ(w;X,y)+αw
更新权重：
w ← w − η ( α w + ▽ w J ( w ; X , y ) ) = ( 1 − η α ) w − η ▽ w J ( w ; X , y ) w\leftarrow w-\eta(\alpha w+\bigtriangledown_wJ(w;X,y))=(1-\eta \alpha)w-\eta \bigtriangledown_wJ(w;X,y) w←w−η(αw+▽wJ(w;X,y))=(1−ηα)w−η▽wJ(w;X,y)
从上式可以看出，加入权重衰减后会导致学习规则的修改，即在每步执行梯度更新前先收缩权重（乘以( 1 − η α 1-\eta \alpha 1−ηα)）
2. L1参数正则化： Ω ( θ ) = ∣ ∣ w ∣ ∣ 1 = Σ i ∣ w i ∣ \Omega(\theta)=||w||_1=\Sigma_i|w_i| Ω(θ)=∣∣w∣∣1=Σi∣wi∣
目标函数：
J ~ ( w ; X , y ) = J ( w ; X , y ) + α ∣ ∣ w ∣ ∣ 1 \tilde{J}(w;X,y)=J(w;X,y)+\alpha||w||_1 J~(w;X,y)=J(w;X,y)+α∣∣w∣∣1
计算梯度：
▽ w J ~ ( w ; X , y ) = ▽ w J ( w ; X , y ) + α s i g n ( w ) \bigtriangledown _w\tilde{J}(w;X,y)=\bigtriangledown_wJ(w;X,y)+\alpha sign(w) ▽wJ~(w;X,y)=▽wJ(w;X,y)+αsign(w)
其中， s i g n ( w ) = { − 1 , w < 0 1 , w > 0 sign(w)=\left\{\begin{matrix} -1 ,& w< 0\\ 1,& w>0 \end{matrix}\right. sign(w)={−1,1,w<0w>0
更新权重：
w ← w − η ( α s i g n ( w ) + ▽ w J ( w ; X , y ) ) w\leftarrow w-\eta(\alpha sign(w)+\bigtriangledown_wJ(w;X,y)) w←w−η(αsign(w)+▽wJ(w;X,y))
二、约束范数惩罚
约束惩罚是指向目标函数中增加额外项来对参数值进行软约束：
{ m i n J ( θ ) s . t . Ω ( θ ) ≤ k \left \{ \begin{matrix} minJ(\theta) \\ s.t. \quad \Omega(\theta)\leq k \end{matrix}\right. {minJ(θ)s.t.Ω(θ)≤k
构造拉格朗日函数：
L ( θ , α ) = J ( θ ) + α ( Ω ( θ ) − k ) L(\theta, \alpha)=J(\theta)+\alpha(\Omega(\theta)-k) L(θ,α)=J(θ)+α(Ω(θ)−k)
原始问题等价于：
θ ∗ = a r g m i n θ max α ; α ≥ 0 L ( θ , α ) \theta^*=\underset{\theta}{argmin} \max_{\alpha;\alpha\geq 0}L(\theta, \alpha) θ∗=θargminα;α≥0maxL(θ,α)
为了洞察约束的影响，我们可以固定 α ∗ \alpha^* α∗，把这个问题看成只跟 θ \theta θ有关的函数：
θ ∗ = a r g m i n θ L ( θ , α ∗ ) = a r g m i n θ J ( θ ; X , y ) + α ∗ Ω ( θ ) \theta^*=\underset{\theta}{argmin} L(\theta, \alpha^*)=\underset{\theta}{argmin} J(\theta;X,y)+\alpha^*\Omega(\theta) θ∗=θargminL(θ,α∗)=θargminJ(θ;X,y)+α∗Ω(θ)
这和最小化 J ~ \tilde{J} J~的正则化训练问题是完全一样的。因此，我们可以把参数范数惩罚看做对权重强加的约束。如果 Ω \Omega Ω是 L 2 L^2 L2范数，那么权重就是被约束在一个 L 2 L^2 L2球中，如果 Ω \Omega Ω是 L 1 L^1 L1范数，那么权重就是被约束在一个 L 1 L^1 L1范数限制的区域中。
三、提前终止
当训练有足够的表示能力甚至会过拟合的大模型时，我们经常观察到，训练误差会随着时间的推移逐渐降低，蛋验证集的误差会再次上升。这意味着我们只要返回使验证集误差最低的参数设置，就可以获得验证集误差更低的模型（并且因此有希望获得更好的测试误差）。
提前终止需要验证集，这意味着某些训练数据不能被馈送到模型。为了更好地利用这一额外的数据，我们可以在完成提前终止的首次训练之后，进行额外的训练。在第二轮，即额外的训练步骤中，所有的训练数据都被包括在内。有两个基本的策略都可以用于第二轮训练过程：
- 一是再次初始化模型，然后使用所有数据再次训练。 在这个第二轮训练过程中，我们使用第一轮提前终止训练确定的最佳步数。但是有一个问题是，我们没有办法知道重新训练时，对参数进行相同次数的更新和对数据集进行相同次数的遍历哪一个更好。由于训练集变大了，在第二次训练时，每一次遍历数据集将会更多次地更新参数。
- 二是保持从第一轮训练获得的参数，然后使用全部的数据继续训练。 在这个阶段，已经没有验证集指导我们需要再训练多少步后终止，取而代之，我们可以监控验证集的平均损失函数，并继续训练，直到它低于提前终止过程终止时的目标值。此策略避免了重新训练模型的高成本，但表现并没有那么好，例如，验证集的目标不一定能达到之前的目标值，所以这种策略甚至不能保证终止。
四、 噪声鲁棒性
大多数数据集的y标签都有一定的错误性。错误的y不利于最大化 log p ( y ∣ x ) \log p(y|x) logp(y∣x)。为避免这种情况发生，一种方法是显示地对标签上的噪声进行建模。
例如，我们可以假设，对于一些小常数 ϵ \epsilon ϵ,训练集标记 y y y是正确的概率为 1 − ϵ 1-\epsilon 1−ϵ，(以 ϵ \epsilon ϵ的概率）任何其他可能的标签也可能是正确的。这个假设很容易就能解析地狱代价函数结合，而不用显式地抽取噪声样本。例如，标签平滑（label smoothing）通过把确切分类目标从0和1替换成 ϵ K − 1 \frac{\epsilon}{K-1} K−1ϵ和 1 − ϵ 1-\epsilon 1−ϵ,正则化具有 K K K个输出的softmax函数的模型。标准交叉熵可以用在这些非确切目标的输出上。使用softmax和明确目标的最大似然学习可能永远不会收敛–softmax函数永远无法真正预测0概率和1概率，因此他会继续学习越来越大的权重，使预测更极端。标签平滑的优势是能够防止模型追求确切概率而不影响模型学习正确分类。
五、半监督学习
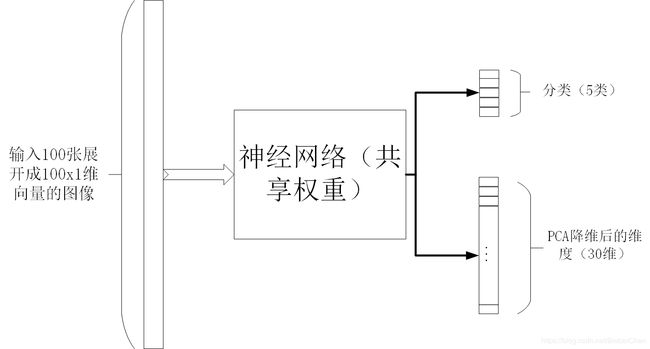
假设有100张 10 × 10 10\times 10 10×10的图片，其中50张有标签（共5类），50张无标签。如果利用普通的神经网络训练时只能够用到50张有标签的图片，而另外50张无标签图像无法使用。
半监督学习的做法是：
- 首先将100维的图像利用PCA降维到30维。
- 利用共享权重的神经网络，有标签的50张图像将标签作为label，无标签的图像将PCA降维后的低维度作为label，如下图所示
六、多任务学习
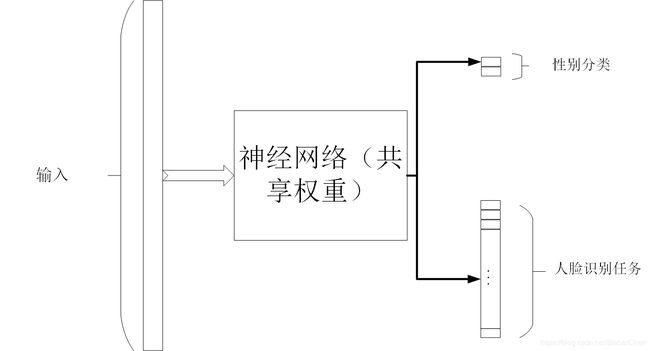
多任务学习是通过合并几个任务中的样例（可以视为对参数施加的软约束）来提高泛化的一种方式。当模型的一部分被多个额外的任务共享时，这部分将被约束为良好的值，通常会带来更好的泛化能力。下图表示了多任务学习的一种普遍形式。不同的监督任务共享相同的输入x和中间层，能学习共同的因素池。从深度学习的观点看，底层的先验知识如下：能解释数据变化（在与之相关联的不同任务中观察到）的因素中，某些因素是夸两个或多个任务共享的，如人脸识别任务与性别分类任务。
七、Bagging及其他集成方法
Bagging（bootstrap aggregating）是通过结合几个模型降低泛化误差的技术。主要想法是分别训练几个不同的模型，然后让所有模型表决测试样例的输出。这机器学习中常规策略的一个例子，被称为模型平均（model averaging）。采用这种策略的技术被称为集成方法。
我们假设有k个回归模型，每个模型在每个例子上的误差是 ϵ i \epsilon_i ϵi，误差服从均值为0、方差为 E [ ϵ i 2 ] = v \mathbb{E}[\epsilon_i^2]=v E[ϵi2]=v、协方差为 E [ ϵ i ϵ j ] = c \mathbb{E}[\epsilon_i\epsilon_j]=c E[ϵiϵj]=c的多维正态分布。通过所有集成模型的平均预测误差为： 1 k Σ i ϵ i \frac{1}{k}\Sigma_i\epsilon_i k1Σiϵi。集成预测器平方误差的期望是：
E [ ( 1 k ∑ i ϵ i ) 2 ] = 1 k 2 E [ ∑ i ( ϵ i 2 + ∑ j ≠ i ϵ i ϵ j ) ] = 1 k v + k − 1 k c \mathbb{E}[(\frac{1}{k}\sum_i\epsilon_i)^2]=\frac{1}{k^2}\mathbb{E}[\sum_i(\epsilon_i^2+\sum_{j\neq i}\epsilon_i\epsilon_j)]=\frac{1}{k}v+\frac{k-1}{k}c E[(k1i∑ϵi)2]=k21E[i∑(ϵi2+j̸=i∑ϵiϵj)]=k1v+kk−1c
在误差完全相关即 c = v c=v c=v的情况下，均方误差减少到 v v v，所以模型平均没有任何帮助。在误差完全不相关即 c = 0 c=0 c=0的情况下，该集成的平方误差的期望仅为 1 k v \frac{1}{k}v k1v。这意味着集成平方误差的期望会随着集成规模增大而线性减少。换言之，平均上，集成至少与它的任何成员表现的一样好，并且如果成员的误差是独立的，集成将显著地比其成员表现得更好。
不同的集成方法以不同的方式构建集成模型。例如，集成的每个成员可以使用不同的算法和目标函数训练成完全不同的模型。Bagging是一种允许重复多次使用同一种模型，训练算法和目标函数的方法。
参考资料：深度学习