opencv3 图像细化算法一(查表法)
8领域骨架提取细化算法
最近偶然看到了一篇博客园上用Python写的图像细化算法,博主写的非常好,于是迫不及待的收藏了。
算法原理啥的就不累述了,博主原文链接:算法原理以及python实现
首先直接上代码(原理博主已经解释的很好了,如果我改过来的代码哪有问题或者不明白的,欢迎交流)
#include
using namespace cv;
Mat ImgSkeletonization(Mat &input_src,Mat &output_dst,int number=20);
//@param number :表示水平方向和垂直方向上“细化的次数”
Mat ImgSkeletonization_H(Mat &input_src,int *search_arr);//水平方向细化
Mat ImgSkeletonization_V(Mat &input_src, int *search_arr);//垂直方向细化
int main()
{
Mat src = imread("sap3.jpg");
Mat src_gray, src_threshold;
cvtColor(src, src_gray, CV_RGB2GRAY);
threshold(src_gray, src_threshold, 170, 255,0);
imshow("src_threshold", src_threshold);
Mat dst;
ImgSkeletonization(src_threshold, dst, 30);
imshow("dst", dst);
waitKey(0);
return 0;
}
Mat ImgSkeletonization(Mat &input_src,Mat & output_dst, int number)
{
output_dst = input_src.clone();
int search_array[]= { 0,0,1,1,0,0,1,1,1,1,0,1,1,1,0,1,\
1,1,0,0,1,1,1,1,0,0,0,0,0,0,0,1,\
0,0,1,1,0,0,1,1,1,1,0,1,1,1,0,1,\
1,1,0,0,1,1,1,1,0,0,0,0,0,0,0,1,\
1,1,0,0,1,1,0,0,0,0,0,0,0,0,0,0,\
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,\
1,1,0,0,1,1,0,0,1,1,0,1,1,1,0,1,\
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,\
0,0,1,1,0,0,1,1,1,1,0,1,1,1,0,1,\
1,1,0,0,1,1,1,1,0,0,0,0,0,0,0,1,\
0,0,1,1,0,0,1,1,1,1,0,1,1,1,0,1,\
1,1,0,0,1,1,1,1,0,0,0,0,0,0,0,0,\
1,1,0,0,1,1,0,0,0,0,0,0,0,0,0,0,\
1,1,0,0,1,1,1,1,0,0,0,0,0,0,0,0,\
1,1,0,0,1,1,0,0,1,1,0,1,1,1,0,0,\
1,1,0,0,1,1,1,0,1,1,0,0,1,0,0,0 };
for (size_t i = 0; i < number; i++)
{
ImgSkeletonization_H(output_dst, &search_array[0]);
ImgSkeletonization_V(output_dst, &search_array[0]);
}
return output_dst;
}
Mat ImgSkeletonization_H(Mat &input_src, int *search_arr)
{
int h = input_src.rows;
int w = input_src.cols;
bool NEXT = true;
for (size_t j = 1; j < w - 1; j++)//注意边界问题!!!!!!
{
for (size_t i = 1; i < h - 1; i++)
{
if (!NEXT)
NEXT = true;
else
{
int judge_value;
if (1 (i - 1, j) + input_src.at(i, j) + input_src.at(i + 1, j);
else
judge_value = 1;
if (input_src.at(i, j) == 0 && judge_value != 0)
{
int a[9] = { 1,1,1,1,1,1,1,1,1};
for (size_t m = 0; m < 3; m++)
{
for (size_t n = 0; n < 3; n++)
{
if ((0 <= (i - 1 + m) < h) && (0 <= (j - 1 + n) < w) && input_src.at(i - 1 + m, j - 1 + n) == 0)
a[m * 3 + n] = 0;
}
}
int sum_value = a[0] * 1 + a[1] * 2 + a[2] * 4 + a[3] * 8 + a[5] * 16 + a[6] * 32 + a[7] * 64 + a[8] * 128;
input_src.at(i, j) = search_arr[sum_value] * 255;
if (search_arr[sum_value] == 1)
NEXT = false;
}
}
}
}
return input_src;
}
Mat ImgSkeletonization_V(Mat &input_src, int *search_arr)
{
int h = input_src.rows;
int w = input_src.cols;
bool NEXT = true;
for (size_t i = 1; i < h - 1; i++)//注意边界问题!!!!!!
{
for (size_t j = 1; j < w - 1; j++)
{
if (!NEXT)
NEXT = true;
else
{
int judge_value;
if (1 < j (i, j - 1) + input_src.at(i, j) + input_src.at(i, j + 1);
else
judge_value = 1;
if (input_src.at(i, j) == 0 && judge_value != 0)
{
int a[9] = {1,1,1,1,1,1,1,1,1 };
for (size_t m = 0; m < 3; m++)
{
for (size_t n = 0; n < 3; n++)
{
if ((0 <= (i - 1 + m) < h) && (0 <= (j - 1 + n) < w) && input_src.at(i - 1 + m, j - 1 + n) == 0)
a[m * 3 + n] = 0;
}
}
int sum_value = a[0] * 1 + a[1] * 2 + a[2] * 4 + a[3] * 8 + a[5] * 16 + a[6] * 32 + a[7] * 64 + a[8] * 128;
input_src.at(i, j) = search_arr[sum_value] * 255;
if (search_arr[sum_value] == 1)
NEXT = false;
}
}
}
}
return input_src;
}
效果如下(图片都是从博主哪里截图来的,如果有原图,加上些去噪操作,效果就会更好了):
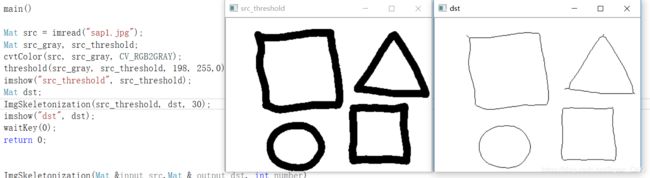

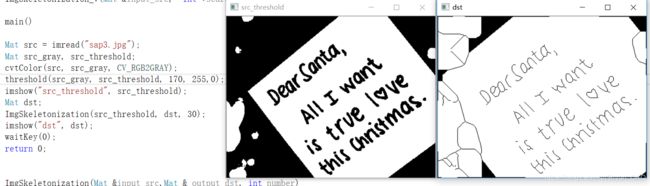
查表法的“表”是怎么来的?
比如要将一个黑色正方形细化,也就是把多余的黑色像素去掉,只留“骨架”,那么怎么判断哪些点能去掉?哪些不能?在考虑八领域的条件下,要去掉的黑色像素周围的像素分布有以下几种位置情况(太多了,只画四个意思意思),对于中间黑色像素的周围的八个位置像素分布而言,每个位置有两种情况:非黑即白(二值图 ),所以总共有2×2×2×2×2×2×2×2=28=256种,所以表中总共的数字有256个,即程序中定义的一个有256个元素的一维数组,数组中0表示不能去掉,1表示能去掉。

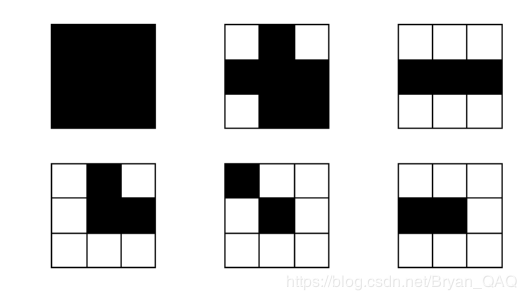
然而,在这256种位置分布中,有一些情况是不能去掉的,有些可以去掉,下面的点中:
第一个点不能去除,因为它是内部点
第二个点不能去除,它也是内部点
第三个点不能去除,删除后会使原来相连的部分断开
第四个点可以去除,这个点不是骨架
第五个点不可以去除,它是直线的端点
第六个点不可以去除,它是直线的端点
将黑色的像素权值设为0,白色的设置为1,白色的每个位置对应的乘数分别为1,2,4,8,16,32,64,128。计算如下右边 中间的黑点是否能去掉:
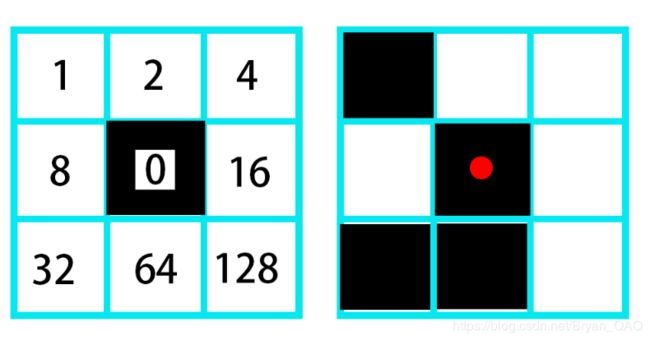
总价值:0×1+1×2+1×4+1×8+1×16+0×32+0×64+1×128=158
查表可以看到:
search_array[158]=0,故该点不可以去掉
算法验证
虽然结果还可以,我还是认真的分析了处理结果,算法还是有不足,比如:先对X方向上细化,还是对Y方向上细化,结果是不同的(不知道是不是我改过来除了啥问题),如下不妨看用红框框住的矩阵(第二种细化结果是我们想要的):
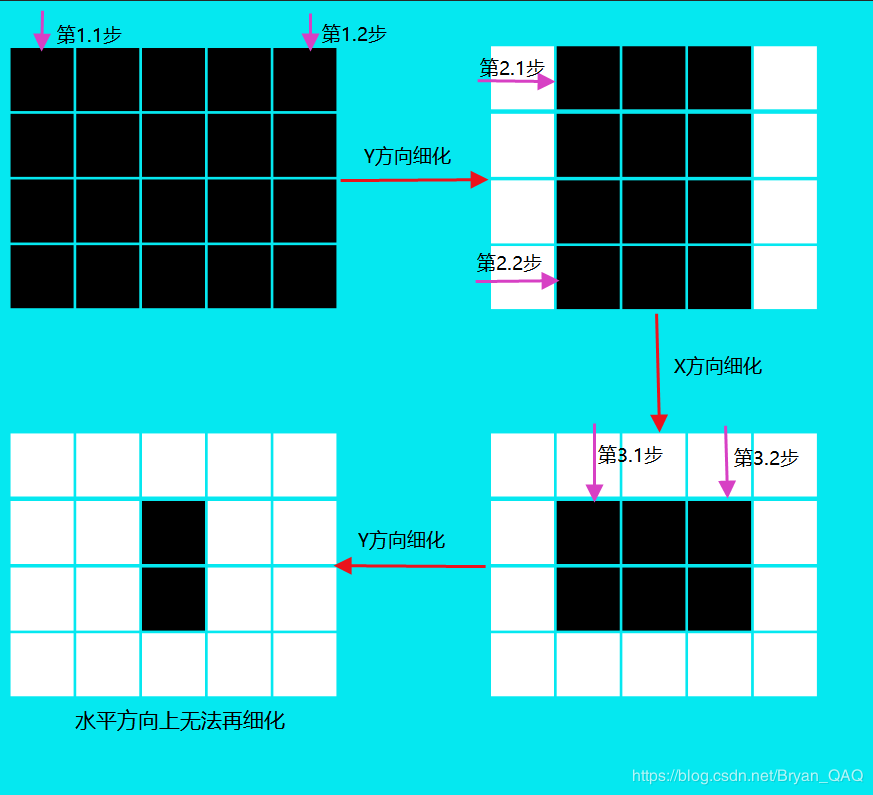
先对Y方向上细化,再对X方向上细化:

上面结果的大致步骤: