RGCN-Modeling Relational Data with Graph Convolutional Networks阅读笔记
作者:来自于 University of Amsterdam 的 Michael Schlichtkrull, Thomas N. Kipf(GCN的作者), Peter Bloem(VU Amsterdam), Rianne van den Berg, Ivan Titov, Max Welling
Abstract
Knowledge graphs enable a wide variety of applications, including question answering and information retrieval. Despite the great effort invested in their creation and maintenance, even the largest (e.g., Yago, DBPedia or Wikidata) remain incomplete. We introduce Relational Graph Convolutional Networks (R-GCNs) and apply them to two standard knowledge base completion tasks: Link prediction (recovery of missing facts, i.e. subject-predicate-object triples) and entity classification (recovery of missing entity attributes). RGCNs are related to a recent class of neural networks operating on graphs, and are developed specifically to deal with the highly multi-relational data characteristic of realistic knowledge bases. We demonstrate the effectiveness of R-GCNs as a stand-alone model for entity classification. We further show that factorization models for link prediction such as DistMult can be significantly improved by enriching them with an encoder model to accumulate evidence over multiple inference steps in the relational graph, demonstrating a large improvement of 29.8% on FB15k-237 over a decoder-only baseline.
知识图谱支持各种应用,包括问答系统和信息检索。尽管在创建和维护上投入了大量精力,但即使是最大的知识库(例如Yago,DBPedia 或 Wikidata)也仍然不完整。我们介绍了关系图卷积网络(R-GCN),并将其应用于两个标准知识库完成任务:链接预测(恢复缺失的事实,即 subject-predicate-object 三元组)和实体分类(丢失实体属性的恢复)。 RGCN与最近一类在图上运行的神经网络有关,是专门为处理现实知识库的高度多关系数据特征而开发的。我们证明了R-GCN作为实体分类的独立模型的有效性。我们进一步表明,通过使用编码器模型丰富它们以在关系图中的多个推理步骤上累积证据,可以显著改善链接预测的因式分解模型(例如DistMult),这表明FB15k-237相对于仅有解码器的基线具有29.8%的大幅改进。
1 Introduction
即使最大的知识库(例如DBPedia,Wikidata或Yago的知识库),尽管在维护方面投入了巨大的精力,但它们仍是不完整的,并且缺乏覆盖范围也损害了下游应用程序。预测知识库中丢失的信息是统计关系学习(statistical relational learning,SRL)的主要重点。
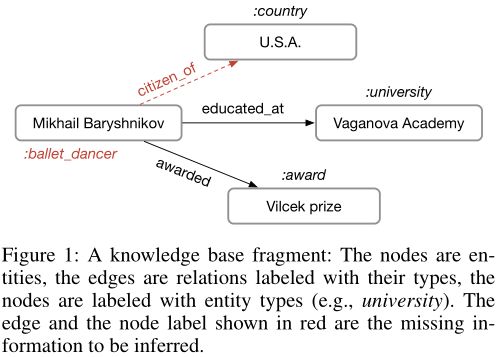
我们考虑两个基本的SRL任务:链接预测(恢复丢失的三元组)和实体分类(为实体分配类型或分类属性)。在这两种情况下,可以预测许多丢失的信息会驻留在通过邻域结构编码的图中,即,知道 Mikhail Baryshnikov 在 Vaganova Academy 受过教育,这意味着 Mikhail Baryshnikov 应该有标签 person,并且三元组(Mikhail Baryshnikov, lived in, Russia)必须属于知识图谱。按照这种直觉,我们为关系图中的实体开发了一个编码器模型,并将其应用于两个任务。
与Kipf and Welling(2017)类似,我们的实体分类模型在图中的每个节点上使用 softmax 分类器。分类器采用关系图卷积网络(R-GCN)提供的节点表示形式并预测标签。通过优化交叉熵损失来学习包括R-GCN参数的模型。
我们的链接预测模型可以看作是一种自动编码器,它由(1)编码器:R-GCN产生实体的潜在特征表示,和(2)解码器:张量分解模型利用这些表示来预测标记的边。 尽管原则上解码器可以依赖于任何类型的因式分解(或通常具有任何评分函数),但我们使用了一种最简单,最有效的因式分解方法:DistMult(Yang等人,2014)。我们观察到,我们的方法在标准基准上取得了竞争性结果,在其他基准方面的表现优于直接优化因式分解(即Vanilla DistMult)。当我们考虑更具挑战性的FB15k-237数据集时(Toutanova和Chen,2015年),这一改进尤其明显。该结果表明,R-GCN中邻居的显式建模(explicit modeling)有助于恢复知识库中缺失的事实。
我们的主要贡献如下。据我们所知,我们是第一个证明 GCN 框架可用于关系数据建模的工具,特别是链接预测和实体分类任务的工具。其次,我们介绍了用于参数共享和实施稀疏性约束的技术,并将其用于将 R-GCN 应用于具有大量关系的多图。最后,我们展示了以 DistMult 为例的分解模型的性能,可以通过在关系图中执行多个信息传播步骤的编码器模型来丰富它们,从而显着提高其性能。
2 Neural relational modeling
我们引入以下符号:我们将有向和标记的多重图表示为 G = ( V , E , R ) G =(\mathcal V,\mathcal E,\mathcal R) G=(V,E,R),其结点(实体)为 v i ∈ V v_i∈\mathcal V vi∈V,标记的边(关系)为 ( v i , r , v j ) ∈ E (v_i,r,v_j)∈\mathcal E (vi,r,vj)∈E,其中 r ∈ R r ∈\mathcal R r∈R 是一个关系类型。
2.1 Relational graph convolutional networks
我们的模型的主要动机是将在局部图邻域上(Duvenaud等,2015; Kipf and Welling,2017)运行的GCN扩展为大规模关系数据。这些以及相关的方法,例如图神经网络(Scarselli等,2009)可以理解为简单的可区分消息传递框架的特殊情况(Gilmer等,2017):
h i ( l + 1 ) = σ ( ∑ m ∈ M i g m ( h i ( l ) , h j ( l ) ) ) (1) h_{i}^{(l+1)}=\sigma\left(\sum_{m \in \mathcal{M}_{i}} g_{m}\left(h_{i}^{(l)}, h_{j}^{(l)}\right)\right)\tag{1} hi(l+1)=σ(m∈Mi∑gm(hi(l),hj(l)))(1)
事实证明,这种类型的转换非常有效地累积和编码来自局部结构化邻域的特征,并在图分类(Duvenaud等人2015)和基于图的半监督学习(Kipf and Welling 2017)等领域取得了显着改善。
受这些架构的启发,我们定义了以下简单的传播模型,用于计算在关系(有向和标记)多重图上用 v i v_i vi 表示的实体或节点的前向更新:
h i ( l + 1 ) = σ ( ∑ r ∈ R ∑ j ∈ N i r 1 c i , r W r ( l ) h j ( l ) + W 0 ( l ) h i ( l ) ) (2) h_{i}^{(l+1)}=\sigma\left(\sum_{r \in \mathcal{R}} \sum_{j \in \mathcal{N}_{i}^{r}} \frac{1}{c_{i, r}} W_{r}^{(l)} h_{j}^{(l)}+W_{0}^{(l)} h_{i}^{(l)}\right)\tag{2} hi(l+1)=σ⎝⎛r∈R∑j∈Nir∑ci,r1Wr(l)hj(l)+W0(l)hi(l)⎠⎞(2)
直观地讲,(2)通过归一化的总和累积相邻节点的变换特征向量。与常规GCN不同,我们引入特定于关系的变换,即取决于边的类型和方向。为了确保也可以通过层 l l l 上的相应表示来通知层 l + 1 l + 1 l+1 上的节点的表示,我们向数据中的每个节点添加了特殊关系类型的单个自连接。注意,不同于简单的线性消息传播,可以选择更灵活的函数,例如多层神经网络(以计算效率为代价)。我们将其留给以后的工作。
神经网络层更新包括对图中的每个节点并行地评估(2)。在实践中,可以使用稀疏矩阵乘法有效地实现(2),以避免在邻域上进行显式求和。可以堆叠多个层以允许跨多个关系步骤的依赖性。我们将此图编码器模型称为关系图卷积网络(R-GCN)。 R-GCN模型中单节点更新的计算图如图2所示。
- 图2:用于计算R-GCN模型中单个图节点/实体(红色)更新的图。收集来自相邻节点(深蓝色)的激活(d维向量),然后分别针对每种关系类型(for both in- and outgoing edges)进行转换。结果表示(绿色)以(标准化的)总和累加并通过激活函数(例如ReLU)传递。可以与整个图上的共享参数并行地计算此每个节点的更新。
2.2 Regularization
将(2)应用于高度多关系的数据时,一个中心问题是图中参数数量和关系数量的快速增长。实际上,这很容易导致对稀有关系的过拟合和非常大的模型。
为了解决这个问题,我们引入了两种单独的方法来规范(归一化) R-GCN 层的权重:基础和块对角线分解(basis- and block-diagonal-decomposition)。通过基分解(basis decomposition),每个 W r ( l ) W^{(l)}_r Wr(l) 定义如下:
W r ( l ) = ∑ b = 1 B a r b ( l ) V b ( l ) (3) W_{r}^{(l)}=\sum_{b=1}^{B} a_{r b}^{(l)} V_{b}^{(l)}\tag{3} Wr(l)=b=1∑Barb(l)Vb(l)(3)
即作为基础变换 V b ( l ) ∈ R d ( l + 1 ) × d ( l ) V^{(l)}_b∈R^{d^{(l + 1)}×d^{(l)}} Vb(l)∈Rd(l+1)×d(l) 与系数 a r b ( l ) a^{(l)}_{rb} arb(l) 的线性组合,使得仅系数取决于 r r r。在块对角分解(block-diagonal decomposition)中,我们通过在一组低维矩阵上的直接求和定义每个 W r ( l ) W^{(l)}_r Wr(l):
W r ( l ) = ⨁ b = 1 B Q b r ( l ) (4) W_{r}^{(l)}=\bigoplus_{b=1}^{B} Q_{b r}^{(l)}\tag{4} Wr(l)=b=1⨁BQbr(l)(4)
基函数分解(3)可以看作是不同关系类型之间有效权重共享的一种形式,而块分解(4)可以看作是每种关系类型对权重矩阵的稀疏约束。块分解结构编码了一种直觉,即可以将潜在特征分组为变量集,这些变量集在组内比在组间更紧密地耦合。两种分解都减少了学习高度多关系数据(例如,现实的知识库)所需的参数数量。同时,我们期望基本参数化可以缓解稀疏关系的过度拟合,因为稀疏关系和更频繁关系之间共享参数更新。
然后,整个R-GCN模型采用以下形式:我们按照(2)的定义堆叠 L L L 层-上一层的输出是下一层的输入。如果不存在其他特征,则可以将第一层的输入选择为图中每个节点的唯一 one-hot 向量。对于块表示,我们通过单个线性变换将此 one-hot 映射为密集表示。然而,我们在这项工作中仅考虑了这种无特征的方法,我们注意到,在 Kipf 和 Welling(2017)中表明,此类模型可以利用预定义的特征向量(例如,与特定节点关联的文档的词袋(bag-of-words)描述)。
3 Entity classification
对于节点(实体)的(半)监督分类,我们只需堆叠形式为(2)的R-GCN层,并在最后一层的输出上激活 s o f t m a x ( ⋅ ) softmax(\cdot) softmax(⋅) 激活(每个节点)。我们将所有标记节点上的以下交叉熵损失最小化(而忽略未标记节点):
L = − ∑ i ∈ Y ∑ k = 1 K t i k ln h i k ( L ) (5) \mathcal{L}=-\sum_{i \in \mathcal{Y}} \sum_{k=1}^{K} t_{i k} \ln h_{i k}^{(L)}\tag{5} L=−i∈Y∑k=1∑Ktiklnhik(L)(5)
其中 Y \mathcal Y Y 是具有标签的节点索引的集合,而 h i k ( L ) h^{(L)}_{ik} hik(L) 是第 i i i 个标记节点的网络输出的第 k k k 个条目。 t i k t_{ik} tik 表示其各自的真实标签。实际上,我们使用(全批次)梯度下降技术训练模型。我们的实体分类模型的示意图在图 3a 中给出。
4 Link prediction
链接预测用于预测新事实(即三元组(subject, relation, object))。形式上,知识库由有向标记图 G = ( V , E , R ) G =(\mathcal V,\mathcal E,\mathcal R) G=(V,E,R) 表示。而不是完整的边 E \mathcal E E,我们只得到了不完整的子集 E ^ \mathcal {\hat E} E^。任务是为可能的边 ( s , r , o ) (s,r,o) (s,r,o) 分配分数 f ( s , r , o ) f(s,r,o) f(s,r,o),以确定这些边属于 E \mathcal E E 的可能性。
为了解决这个问题,我们引入了图自动编码器模型,该模型由实体编码器和评分函数(解码器)组成。编码器将每个实体 v i ∈ V v_i∈\mathcal V vi∈V 映射到实值向量 e i ∈ R d e_i∈R^d ei∈Rd。解码器根据顶点表示重建图的边;换句话说,它通过函数 s : R d × R × R d → R s:R^d×R×R^d→R s:Rd×R×Rd→R 对 (subject, relation, object)-triples 进行评分。链接预测的大多数现有方法(例如张量和神经分解方法(Socher等人,2013;Lin等。 2015; Toutanova等。 2016;扬等。 2014; Trouillon等。 2016))可以在此框架下进行解释。我们工作的关键区别特征是对编码器的依赖。尽管大多数先前的方法针对直接在训练中优化的每个 v i ∈ V v_i∈\mathcal V vi∈V 使用单个实值向量 e i e_i ei,但我们通过 e i = h i ( L ) e_i = h^{(L)}_i ei=hi(L) 的 R-GCN 编码器来计算表示形式,类似于在图2中引入的图自动编码器模型 Kipf和Welling(2016)的未标记无向图。我们的全链接预测模型如图 3b 所示。
在我们的实验中,我们使用 DistMult 因子分解(Yang等人,2014)作为评分函数,众所周知,当单独使用时,该函数在标准链接预测基准上表现良好。在 DistMult 中,每个关系 r r r 与对角矩阵 R r ∈ R d × d R_r∈R^{d×d} Rr∈Rd×d 关联,并且将三元组 ( s , r , o ) (s,r,o) (s,r,o) 记为
f ( s , r , o ) = e s T R r e o (6) f(s, r, o)=e_{s}^{T} R_{r} e_{o}\tag{6} f(s,r,o)=esTRreo(6)
正如先前关于分解的工作(Yang等人,2014; Trouillon等人,2016)一样,我们使用负采样来训练模型。对于每个观察到的例子,我们对 ω ω ω 负样本进行采样。我们通过随机破坏每个正面示例的主题或对象来进行采样。我们针对交叉熵损失进行了优化,以使模型的可观察三元组得分高于负三元组:
L = − 1 ( 1 + ω ) ∣ E ^ ∣ ∑ ( s , r , o , y ) ∈ T y log l ( f ( s , r , o ) ) + ( 1 − y ) log ( 1 − l ( f ( s , r , o ) ) ) \begin{array}{rl} \mathcal{L}=-\frac{1}{(1+\omega)|\hat{\mathcal{E}}|} \sum_{(s, r, o, y) \in \mathcal{T}} & y \log l(f(s, r, o)) +(1-y) \log (1-l(f(s, r, o))) & \end{array} L=−(1+ω)∣E^∣1∑(s,r,o,y)∈Tylogl(f(s,r,o))+(1−y)log(1−l(f(s,r,o)))
其中 T \mathcal T T 是真实和损坏的三元组的总集合, l l l 是 logistic sigmoid function, y y y 是一个指示符, y = 1 y=1 y=1 对于正的三元组, y = 0 y = 0 y=0,对于负的三元组。
5 Empirical evaluation
5.1 Entity classification experiments
在这里,我们考虑在知识库中对实体进行分类的任务。为了推断一个实体的类型(例如,个人或公司),成功的模型需要推理出该实体所涉及的与其他实体的关系。
Datasets 我们以资源描述框架(RDF)格式(Ristoski,de Vries和Paulheim 2016)的四个数据集3评估了模型:AIFB,MUTAG,BGS和AM。这些数据集中的关系不必一定要编码定向的主客关系,而是还可以用来编码给定实体是否存在特定特征。在每个数据集中,要分类的目标是表示为节点的一组实体的属性。数据集的确切统计信息可以在表1中找到。有关数据集的更详细说明,读者可以参考Ristoski,de Vries和Paulheim(2016)。我们删除了用于创建实体标签的关系:AIFB的 employs and affil-
iation ,MUTAG的isMutagenic,BGS的hasLithogenesis和AM的objectCategory和material。
Baselines 作为我们实验的基线,我们将RDF2Vec嵌入(Ristoski和Paulheim,2016),Weisfeiler-Lehman核(WL)(Shervashidze等人,2011; de Vries和de Rooij)的最新分类结果进行比较2015)和手工设计的特征提取器(Feat)(Paulheim andFümkranz2012)。 Feat根据每个标记实体的入度和出度(每个关系)组合特征向量。 RDF2Vec提取在标记图上行走,然后使用Skipgram(Mikolov等人,2013)模型进行处理,以生成实体嵌入,用于后续分类。参见Ristoski和Paulheim(2016)对这些基准方法的深入描述和讨论。所有实体分类实验均在具有64GB内存的CPU节点上运行。
Results 表2中的所有结果均记录在Ristoski,de Vries和Paulheim(2016)的训练/测试基准划分中。我们还预留了训练集的20%作为超参数调整的验证集。对于R-GCN,我们报告一个2层模型的性能,该模型具有16个隐藏单元(AM为10个),基函数分解(方程3),并使用学习率由Adam(Kingma和Ba 2014)训练了50个时期为0.01。归一化常数选择为 c i , r = ∣ N i T ∣ c_{i,r} = | N^\mathcal T _i | ci,r=∣NiT∣。补充材料中提供了有关(基线)模型和超参数选择的更多详细信息。
我们的模型在AIFB和AM上获得了最新的结果。为了解释MUTAG和BGS在性能上的差距,重要的是要了解这些数据集的性质。 MUTAG是分子图的数据集,后来被转换为RDF格式,其中关系要么表示原子键,要么仅表示某个特征的存在。 BGS是具有分层特征描述的岩石类型数据集,该特征描述类似地转换为RDF格式,其中关系对某个特征或特征层次的存在进行编码。 MUTAG和BGS中标记的实体仅通过对特定功能进行编码的高度集线器节点连接。
我们推测,归因于来自相邻节点的消息聚合的归一化常数的固定选择部分归咎于此行为,这对于高度节点可能尤其成问题。克服此限制的一种潜在方法是引入一种关注机制,即用依赖于数据的注意力权重 a i j , r a_{ij,r} aij,r 代替归一化常数 1 / c i , r 1 / c_{i,r} 1/ci,r,其中 ∑ j , r a i j , r = 1 \sum _ {j,r}a_{ij,r}=1 ∑j,raij,r=1。我们希望这是一个有前途的研究途径。
5.2 Link prediction experiments
如上一节中所示,R-GCN充当关系数据的有效编码器。现在,我们将编码器模型与评分函数(我们将其称为解码器,请参见图3b)结合起来,对候选三元组进行评分,以进行知识库中的链接预测。
7 Conclusions
我们介绍了关系图卷积网络(R-GCN),并在两个标准统计关系建模问题的背景下证明了它们的有效性:链接预测和实体分类。对于实体分类问题,我们已经证明 R-GCN 模型可以充当竞争性,端到端可训练基于图的编码器。对于链路预测,以 DistMult 因式分解为解码组件的 R-GCN 模型的性能优于因式分解模型的直接优化,并在标准链路预测基准上获得了有竞争力的结果。对于具有挑战性的 FB15k-237 数据集,事实证明,使用RGCN编码器丰富分解模型尤其有价值,与仅解码器的基准相比,改进了29.8%。
有几种方法可以扩展我们的工作。例如,可以将图自动编码器模型与其他因式分解模型(例如ComplEx(Trouillon等人2016))结合使用,该模型可能更适合于建模非对称关系。将实体特征集成到R-GCN中也很简单,这对于链接预测和实体分类问题都将是有益的。为了解决我们方法的可扩展性,有必要探索下采样(sub-sampling)技术,例如 Hamilton,Ying和Leskovec(2017)。最后,将有希望的是,以依赖于数据的注意力机制取代当前在相邻节点和关系类型上求和的形式。除了建模知识库之外,R-GCN 可以推广到其他应用中,在这些应用中关系分解模型已被证明是有效的(例如关系提取)。
代码实现:Github链接
作者演讲视频
RGCN - Modeling Relational Data with Graph Convolutional Networks 使用图卷积网络对关系数据进行建模 ESWC 2018