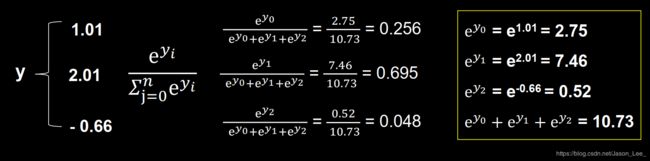ML&DL - TensorFlow2.1快速入门学习笔记
ML&DL - TensorFlow2.1快速入门学习笔记
- 第一讲 神经网络计算
- 1.1 人工智能三学派
- 1.2 神经网络设计过程
- 梯度下降法
- 梯度下降法的缺点
- 1.3 张量 (Tensor)
- 1. 张量
- 2. 数据(张量)类型
- 3. 张量生成
- 1.4 TensorFlow2常用函数(1)
- 强制转换数据类型,最大、最小值,平均值,求和
- axis参数:
- 可训练参数 tf.Variable
- TensorFlow中的数学运算
- 数据/标签对 数据集构建
- 1.5 TensorFlow2常用函数(2)
- 自动求导机制 tf.GradientTape()
- 枚举函数 enumerate()
- 独热编码 (one-hot encoding)
- softmax 逻辑回归
- 自更新函数 tf.assign_*()
- 求取最大值索引 tf.argmax()
- 1.6 使用神经网络实现鸢尾花分类
- 读入Iris数据集
- 第二讲 神经网络优化
- 2.1 预备知识
- 基础函数
- tf.where()
- np.random.RandomState.rand()
- np.vstack()
- ① np.mgrid[ ]; ② .ravel( ); ③ np.c_[ ]
- 2.2 神经网络复杂度
- 2.3 指数衰减学习率
- 2.4 激活函数
- 常用的激活函数
- Sigmoid激活函数
- Tanh激活函数
- Relu激活函数
- Leaky Relu激活函数
- 初学者激活函数选择
- 2.5 损失函数
- 均方误差(Mean Square Error, MSE)损失函数
- 自定义损失函数
- 交叉熵(Cross Entropy, CE)损失函数
- Softmax与交叉熵
- 2.6 欠拟合与过拟合
- 正则化(Regularization)缓解过拟合
- 2.7 神经网络参数优化器
- 准备知识 待优化参数 w w w,损失函数 l o s s loss loss,学习率 l r lr lr;批batch
- 关于batch设置:
- 随机梯度下降(stochastic gradient descent,SGD)
- 含动量的随机梯度下降(SGD + the first-order Momentum,SGDM)
- Adagrad(SGD + the second-order Momentum)
- RMSProp(SGD + the second-order Momentum)
- Adam(SGD + the first-order Momentum + the second-order Momentum)
- 优化器选择
- 第三讲 神经网络八股
- 3.1 搭建网络八股 Sequential
- 神经网络搭建“六步法”
- Sequential()
- compile()
- fit()
- summary()
- 3.2 搭建网络八股 class
- 3.3 MNIST数据集
- 3.4 FASHION数据集
- 第四讲 神经网络八股扩展
- 4.1 自建数据集
- 4.2 数据增强
- 4.3 断点续训
- 保存模型
- 读取模型
- 4.4 参数提取
- 4.5 acc & loss 可视化
- 4.6 应用程序:给图识物
- 第五讲 卷积神经网络
- 5.1 卷积计算过程
- 5.2 感受野
- 5.3 全零填充
- 5.4 TensorFlow实现卷积计算层
- 5.5 批标准化 (Batch Normalization, BN)
- 5.6 池化
- 5.7 舍弃 Dropout
- 5.8 卷积神经网络
- 卷积是什么?
- 5.9 CIFAR10数据集
- 5.10 卷积神经网络搭建示例
- 5.11 LeNet、AlexNet、VGGNet、InceptionNet、ResNet
- LeNet
- AlexNet
- VGGNet
- InceptionNet
- Inception结构块
- 搭建一个精简的 InceptionNet
- ResNet
- 跳跃连接 与 ResNet 结构块
- 跳跃连接的两种方式
- 搭建 ResNet-18
- 5.12 经典卷积神经网络小结
- 第六讲 循环神经网络 (Recurrent Neural Network, RNN)
- 6.1 循环核
- 6.2 循环核按照时间步展开
- 6.3 循环计算层
- 6.4 TensorFlow描述循环计算层
- 6.5 循环计算过程Ⅰ
- 6.6 TensorFlow实现字母预测任务Ⅰ
- 6.7 循环计算过程Ⅱ
- 6.8 TensorFlow实现字母预测任务Ⅱ
- 关于 x_train 维度、记忆体个数
- 6.9 Embedding 编码
- 6.10 TensorFlow实现字母预测任务——使用Embedding编码
- 6.13 长短时记忆网络 (Long Short-Term Memory, LSTM)
- 长期依赖问题
- References
第一讲 神经网络计算
1.1 人工智能三学派
人工智能:让机器具备人的思维和意识。
人工智能三学派:
- 行为主义:基于控制论,构建感知-动作控制系统。 (控制论,
如平衡、行走、避障等自适应控制系统) - 符号主义:基于算数逻辑表达式,求解问题时先把问题描述为
表达式,再求解表达式。 (可用公式描述、实现理性思维,如专家系统) - 连接主义:仿生学,模仿神经元连接关系。 (仿脑神经元连接,
实现感性思维,如神经网络)
神经网络设计步骤:
- 准备数据:采集大量“特征/标签” 数据
- 搭建网络:搭建神经网络结构
- 优化参数:训练网络获取最佳参数(反传)
- 应用网络:将网络保存为模型,输入新数据,输出分类或预测结果(前传)
1.2 神经网络设计过程
梯度下降法
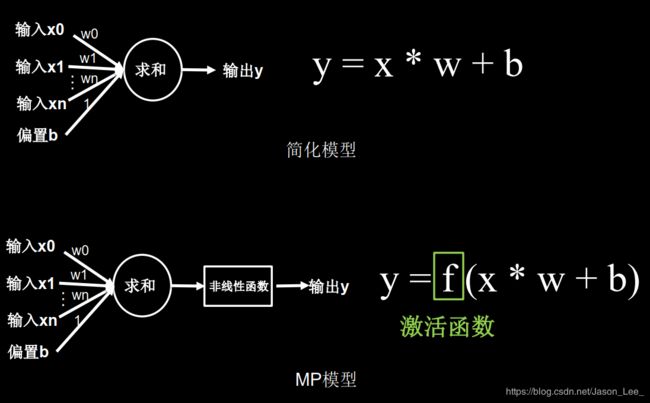
下图为神经网络模型中的神经元的结构:
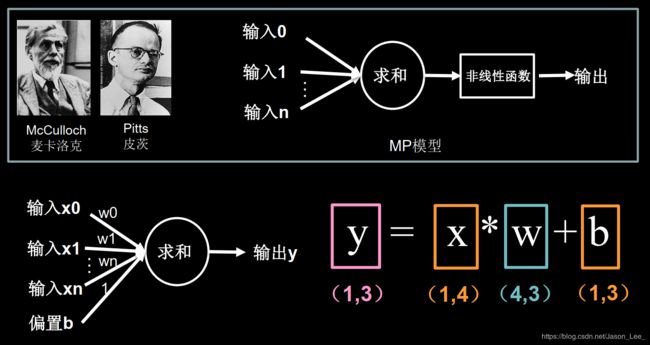
目的: 找到一组最优参数权重 W W W 和偏置 b b b ,是的损失函数最小。
梯度: 函数对各参数求偏导后的向量。
函数梯度下降的方向就是函数值减小的方向。
梯度下降法: 沿着损失函数梯度下降的方向,寻找损失函数的最小值,得到最优参数的方法。
损失函数 (Loss Function): 预测值 ( y y y) 与标准答案 ( y ^ \hat{y} y^) 之间的差距。
损失函数可以用来定量描述 W W W、 b b b 的优劣,当损失函数输出值最小时,参数 W W W、 b b b 会取得最优值。
学习率 (Learning rate, η \eta η): 是一个超参数,决定了参数每次更新的幅度。合适的学习率能够使目标函数在合适的时间内收敛到局部最小值。参数更新公式为: θ n + 1 = θ n − η ∂ l o s s ( θ n ) ∂ θ n \theta_{n+1}=\theta_n-\eta\frac{\partial{loss(\theta_n)}}{\partial{\theta_n}} θn+1=θn−η∂θn∂loss(θn)学习率设置过小会导致模型收敛很慢,学习率设置过大会导致参数值在最优值两侧来回震荡。

前向传播: 从前向后,神经网络根据输入 x x x和网络参数得到输出 y y y的过程。
可将神经网络前向传播表述为如下表达式: y = W ∗ x + b (1) y=W*x+b\tag{1} y=W∗x+b(1)
反向传播: 从后向前,神经网络逐层求损失函数对神经元参数的偏导数,迭代更新所有参数的过程。
根据以上概念,可以将使用梯度下降法进行反向传播的过程表述为:
w t + 1 = w t − η ∗ ∂ l o s s ∂ w t b t + 1 = b t − η ∗ ∂ l o s s ∂ b t w t + 1 ∗ x + b t + 1 → y (2) \begin{aligned} & w_{t+1}=w_t-\eta*\frac{\partial loss}{\partial w_t} \\ & b_{t+1}=b_t-\eta*\frac{\partial loss}{\partial b_t} \\ & w_{t+1}*x+b_{t+1}\rarr y \end{aligned} \tag{2} wt+1=wt−η∗∂wt∂lossbt+1=bt−η∗∂bt∂losswt+1∗x+bt+1→y(2)
举个栗子:
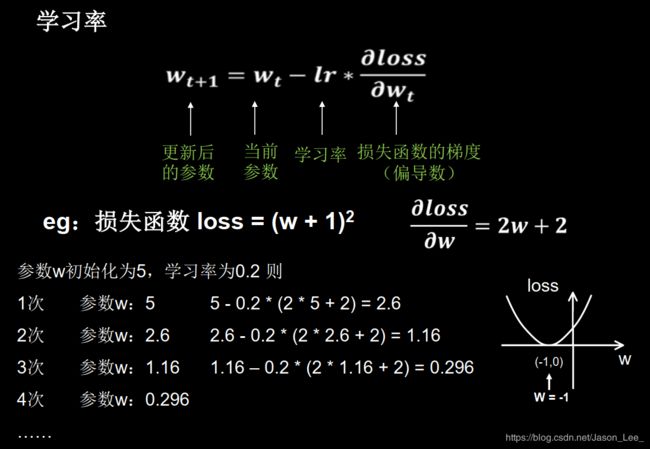
损失函数: l o s s = ( w + 1 ) 2 loss=(w+1)^2 loss=(w+1)2,求偏导: ∂ l o s s ∂ w = 2 w + 2 \frac{\partial loss}{\partial w}=2w+2 ∂w∂loss=2w+2
则反向传播计算过程如下:

梯度下降法的缺点
梯度下降法并不能保证被优化的函数达到全局最优解。例如下图中所给出的函数形式,在⭕处偏导为0,参数不会进一步更新,所以使用梯度下降法只能达到局部最优解而非全局最优解。在这种情况下,参数的初始值会在很大程度上影响最终结果。
只有在损失函数为凸函数的情况下,梯度下降法才能保证达到全局最优解。
1.3 张量 (Tensor)
TensorFlow2.0发展历程:
2019年 3 月 Tensorflow 2.0 测试版发布
2019年10月 Tensorflow 2.0 正式版发布
2020年 1 月 Tensorflow 2.1 发布
1. 张量
张量 (Tensor): 多维数组(列表),可以表示0阶到n阶的数组。
张量的阶: 张量的维数
| 维数 | 阶 | 名字 | 例子 |
|---|---|---|---|
| 0-D | 0 | 标量 | scalar s = 1 2 3 |
| 1-D | 1 | 向量 | vector v = [1, 2, 3] |
| 2-D | 2 | 矩阵 | matrix m = [ [1, 2, 3], [4, 5, 6], [7, 8, 9] ] |
| n-D | n | 张量 | tensor t = [ […n个… [ [ |
2. 数据(张量)类型
tf.int (整型) , tf.float (浮点型) ……
tf.int 32, tf.int64, tf.float 32, tf.float 64
tf.bool (布尔型)
tf.constant([True, False])
tf.string (字符串)
tf.constant(“Hello, world!”)
3. 张量生成
(1) 创建普通(常量)张量:
# dtype=参数可省略,默认数据类型为 tf.int32
tf.constant(张量值, dtype=数据类型(可省略))
运行如下代码:
import tensorflow as tf
a = tf.constant([1, 5], dtype=tf.int64)
print('a:', a, '\na.dtype:', a.dtype, '\na.shape:', a.shape)
运行结果:
a: tf.Tensor([1 5], shape=(2,), dtype=int64)
a.dtype: <dtype: 'int64'>
a.shape: (2,)
(2) 将numpy中的数据类型转换为Tensor数据类型
tf.convert_to_tensor(数据名, dtype=数据类型(可省略))
运行如下代码:
import tensorflow as tf
import numpy as np
a = np.arange(0, 5)
b = tf.convert_to_tensor(a, dtype=tf.int64)
print("a:", a, "\na.type:", type(a))
print("b:", b, "\nb.type:", type(b))
运行结果:
a: [0 1 2 3 4]
a.type: <class 'numpy.ndarray'>
b: tf.Tensor([0 1 2 3 4], shape=(5,), dtype=int64)
b.type: <class 'tensorflow.python.framework.ops.EagerTensor'>
(3) 其他常用的张量创建函数
# 创建全为0的张量
tf. zeros(维度)
# 创建全为1的张量
tf. ones(维度)
# 创建全为指定值的张量
tf. fill(维度, 指定值)
指定维度:
一维 tf.zeros(5)
二维 tf.zeros([行,列])
多维 tf.zeros([n, m, j, k, …])
运行如下代码:
import tensorflow as tf
a = tf.zeros([2, 3])
b = tf.ones(4)
c = tf.fill([2, 2], 9)
print("a:", a)
print("b:", b)
print("c:", c)
运行结果:
tf.Tensor([[0. 0. 0.] [0. 0. 0.]], shape=(2, 3), dtype=float32)
tf.Tensor([1. 1. 1. 1.], shape=(4, ), dtype=float32)
tf.Tensor([[9 9] [9 9]], shape=(2, 2), dtype=int32)
创建随机张量:
# 生成正态分布的随机数,默认均值为0,标准差为1
tf.random.normal(维度, mean=均值(可省略), stddev=标准差(可省略))
# 生成截断式正态分布的随机数
tf.random.truncated_normal(维度, mean=均值(可省略), stddev=标准差(可省略))
# 生成 [minval, maxval) 区间内均匀分布随机数
tf.random.uniform(维度, minval=最小值, maxval=最大值)
在tf.truncated_normal中如果随机生成数据的取值在 ( μ − 2 σ , μ + 2 σ ) (μ-2σ, μ+2σ) (μ−2σ,μ+2σ)之外,则重新进行生成,保证了生成值在均值附近。其中, μ μ μ:均值, σ = ∑ i = 1 n ( x i − x ˉ ) 2 n σ=\sqrt{\frac{\sum_{i=1}^n (x_i-\bar{x})^2}{n}} σ=n∑i=1n(xi−xˉ)2:标准差。
1.4 TensorFlow2常用函数(1)
强制转换数据类型,最大、最小值,平均值,求和
# 强制tensor转换为该数据类型
tf.cast(张量名, dtype=数据类型)
# 计算张量维度上元素的最小值
tf.reduce_min(张量名)
# 计算张量维度上元素的最大值
tf.reduce_max(张量名)
# 计算张量沿着指定维度的平均值
tf.reduce_mean (张量名, axis=操作轴)
# 计算张量沿着指定维度的和
tf.reduce_sum (张量名, axis=操作轴)
tf.reduce_** 中的reduce是指降维,通过这些操作会降低张量维度。
举个栗子:
import tensorflow as tf
x1 = tf.constant([1., 2., 3.], dtype=tf.float64)
print("x1:", x1)
x2 = tf.cast(x1, tf.int32)
print("x2:", x2)
print("minimum of x2:", tf.reduce_min(x2))
print("maxmum of x2:", tf.reduce_max(x2))
运行结果:
x1: tf.Tensor([1. 2. 3.], shape=(3,), dtype=float64)
x2: tf.Tensor([1 2 3], shape=(3,), dtype=int32)
minimum of x2: tf.Tensor(1, shape=(), dtype=int32)
maxmum of x2: tf.Tensor(3, shape=(), dtype=int32)
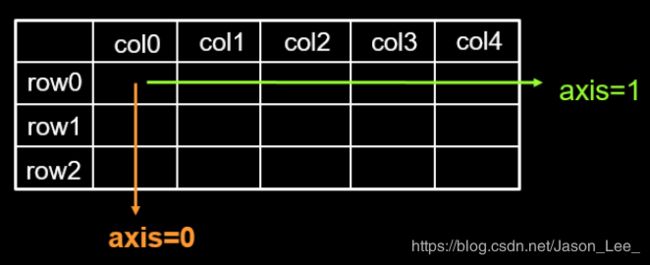
axis参数:
在一个二维张量或数组中,可以通过调整 axis 等于0或1 控制执行维度。
axis=0代表跨行(经度, down),即对列进行操作;
axis=1代表跨列(纬度, across),即对行进行操作;
该参数可省略,如果不指定axis,则张量中所有元素参与计算。
可训练参数 tf.Variable
tf.Variable(初始值)
w = tf.Variable(tf.random.normal([2, 2], mean=0, stddev=1))
将变量标记为“可训练” ,被标记的变量会在反向传播中记录梯度信息。 神经网络训练中,常用该函数标记待训练参数。
TensorFlow中的数学运算
两个张量对应元素的四则运算:只有维度相同的张量才可以做四则运算
tf.add, tf.subtract, tf.multiply, tf.divide
# 实现两个张量的对应元素相加
tf.add(张量1,张量2)
# 实现两个张量的对应元素相减
tf.subtract(张量1,张量2)
# 实现两个张量的对应元素相乘
tf.multiply(张量1,张量2)
# 实现两个张量的对应元素相除
tf.divide(张量1,张量2)
平方、次方与开方: tf.square, tf.pow, tf.sqrt
# 计算某个张量的平方
tf.square(张量名)
# 计算某个张量的n次方
tf.pow(张量名, n次方)
# 计算某个张量的开平方
tf.sqrt(张量名)
矩阵乘法: tf.matmul
# 实现两个矩阵的相乘
tf.matmul(矩阵1, 矩阵2)
数据/标签对 数据集构建
神经网络训练时需要将 输入特征 和 标签 配对后输入网络。
下面的函数实现切分传入张量的第一维度,生成输入特征/标签对,构建数据集。
# Numpy和Tensor格式数据类型都可使用该语句
data = tf.data.Dataset.from_tensor_slices((输入特征, 标签))
举个栗子:
import tensorflow as tf
features = tf.constant([12, 23, 10, 17])
labels = tf.constant([0, 1, 1, 0])
dataset = tf.data.Dataset.from_tensor_slices((features, labels))
for element in dataset:
print('type:', type(element), element)
运行结果:
type: <class 'tuple'> (<tf.Tensor: shape=(), dtype=int32, numpy=12>, <tf.Tensor: shape=(), dtype=int32, numpy=0>)
type: <class 'tuple'> (<tf.Tensor: shape=(), dtype=int32, numpy=23>, <tf.Tensor: shape=(), dtype=int32, numpy=1>)
type: <class 'tuple'> (<tf.Tensor: shape=(), dtype=int32, numpy=10>, <tf.Tensor: shape=(), dtype=int32, numpy=1>)
type: <class 'tuple'> (<tf.Tensor: shape=(), dtype=int32, numpy=17>, <tf.Tensor: shape=(), dtype=int32, numpy=0>)
1.5 TensorFlow2常用函数(2)
自动求导机制 tf.GradientTape()
以下代码实现了求取 y ( x ) = x 2 y(x)=x^2 y(x)=x2在 x = 3 x=3 x=3处的导数:
import tensorflow as tf
x = tf.Variable(initial_value=3., cls=float32)
with tf.GradientTape() as tape: # 在 tf.GradientTape() 的上下文内,所有计算步骤都会被记录以用于求导。
y = tf.square(x)
y_grad = tape.gradient(y, x) # 计算y关于x的导数
print([y, y_grad])
运行结果:
[<tf.Tensor: shape=(), dtype=float32, numpy=9.0>, <tf.Tensor: shape=(), dtype=float32, numpy=6.0>]
枚举函数 enumerate()
enumerate(列表名) 函数用于将一个可遍历的数据对象(如列表、元组或字符串)组合为一个索引序列,同时列出数据和数据下标(格式为:索引 元素),一般用在 for 循环当中。
seq = ['one', 'two', 'three']
for i, element in enumerate(seq):
print(i, element)
for dataset in enumerate(seq):
# 返回元组tuple
print(dataset)
运行结果:
0 one
1 two
2 three
(0, 'one')
(1, 'two')
(2, 'three')
独热编码 (one-hot encoding)
在分类问题中,常用独热码做标签,标记类别: 1表示是, 0表示非。
tf.one_hot() 函数将待转换数据,转换为one-hot形式的数据输出。
tf.one_hot (待转换数据, depth=类别数)
举个栗子:
import tensorflow as tf
classes = 4
labels = tf.constant([1, 0, 3]) # 输入的元素值最小为0,最大为3(0~3一共4个类别)
output = tf.one_hot(labels, depth=classes)
print("result of labels:", output)
运行结果:
result of labels: tf.Tensor(
[[0. 1. 0. 0.]
[1. 0. 0. 0.]
[0. 0. 0. 1.]], shape=(3, 4), dtype=float32)
softmax 逻辑回归
神经网络前向传播的结果,需要变换为概率分布,才可与one-hot编码进行比较。softmax 逻辑回归计算公式: softmax ( y i ) = e y i ∑ j = 0 n e y i \text{softmax}(y_i)=\frac{e^{y_i}}{\sum_{j=0}^n e^{y_i}} softmax(yi)=∑j=0neyieyiTensorFlow实现:
tf.nn.softmax(y) # 使输出符合概率分布
当 n 分类的 n 个输出 ( y 0 , y 1 , … … , y n − 1 ) (y_0 , y_1, ……, y_{n-1}) (y0,y1,……,yn−1) 通过softmax()函数后,其符合概率分布 ∀ y , P ( Y = y ) ∈ [ 0 , 1 ] , 且 ∑ P ( Y = y ) = 1 \forall{y}, P(Y=y)\in[0,1], 且\sum{P(Y=y)=1} ∀y,P(Y=y)∈[0,1],且∑P(Y=y)=1
自更新函数 tf.assign_*()
tf.assign_sub() 实现自减赋值操作,更新参数的值并返回。
调用assign_sub前,先用 tf.Variable 定义变量为可训练的(可自更新)。
举个栗子:
import tensorflow as tf
x = tf.Variable(tf.constant(4))
x.assign_sub(1)
print("x:", x) # 4-1=3
运行结果:
x: <tf.Variable 'Variable:0' shape=() dtype=int32, numpy=3>
求取最大值索引 tf.argmax()
tf.argmax(张量名, axis=操作轴) 返回张量沿指定维度最大值的索引。
tf.reduce_max(张量名, axis=操作轴) 返回张量沿指定维度的最大值。
1.6 使用神经网络实现鸢尾花分类
鸢尾花数据集 (Iris) 介绍:
共有数据150组,每组包括花萼长、花萼宽、花瓣长、花瓣宽4个输入特征。同时给出了,这一组特征对应的鸢尾花类别。类别包括Setosa Iris(狗尾草鸢尾), Versicolour Iris(杂色鸢尾), Virginica Iris(弗吉尼亚鸢尾)三类,分别用数字0, 1, 2表示。

读入Iris数据集
从 sklearn 包 datasets 读入数据集:
from sklearn.datasets import load_iris
x_data = datasets.load_iris().data # 返回iris数据集所有输入特征
y_data = datasets.load_iris().target # 返回iris数据集所有标签
神经网络训练代码:p45_iris.py
第二讲 神经网络优化
2.1 预备知识
基础函数
tf.where()
# 条件语句真返回A,条件语句假返回B
tf.where(条件语句,真返回A,假返回B)
举个栗子:
a=tf.constant([1, 2, 3, 1, 1])
b=tf.constant([0, 1, 3, 4, 5])
c=tf.where(tf.greater(a, b), a, b) # 若a>b,返回a对应位置的元素,否则
返回b对应位置的元素
print("c:",c)
运行结果:
c: tf.Tensor([1 2 3 4 5], shape=(5,), dtype=int32)
np.random.RandomState.rand()
# 返回一个[0,1)之间的随机数
np.random.RandomState.rand(维度) # 若维度为空,则返回标量
举个栗子:
import numpy as np
rdm = np.random.RandomState(seed=1) # seed=常数,每次生成随机数相同
a = rdm.rand() # 返回一个随机标量
b = rdm.rand(2, 3) # 返回维度为2行3列随机数矩阵
print("a:", a)
print("b:", b)
运行结果:
a: 0.417022004702574
b: [[7.20324493e-01 1.14374817e-04 3.02332573e-01]
[1.46755891e-01 9.23385948e-02 1.86260211e-01]]
np.vstack()
# 将两个数组按垂直方向叠加
np.vstack(数组1, 数组2)
举个栗子:
import numpy as np
a = np.array([1, 2, 3])
b = np.array([4, 5, 6])
c = np.vstack((a, b))
print("c:\n", c)
运行结果:
c:
[[1 2 3]
[4 5 6]]
① np.mgrid[ ]; ② .ravel( ); ③ np.c_[ ]
这三个函数、方法通常一起使用,用于生成空间网格坐标点。
# np.mgrid[] 返回间隔数值点,可同时返回多组。左闭右开:[起始值 结束值)
np.mgrid[第1维, 第2维, 第3维, ……]
# x.ravel( ) 将x变为一维数组,“把. 前变量拉直”
x.ravel()
# np.c_[ ] 使返回的间隔数值点配对
np.c_[数组1, 数组2, ……]
np.mgrid[]有两种使用方法
# 以p为步长生成数组,左闭右开:[m, n)
np.mgrid[m, n, p]
# 在区间[m, n]内取p个点
np.mgrid[m, n, pj]
举个栗子:
import numpy as np
# 生成等间隔数值点
x, y = np.mgrid[1:3:1, 2:4:0.5]
# 将x, y拉直,并合并配对为二维张量,生成二维坐标点
grid = np.c_[x.ravel(), y.ravel()]
print("x:\n", x)
print("y:\n", y)
print("x.ravel():\n", x.ravel())
print("y.ravel():\n", y.ravel())
print('grid:\n', grid)
运行结果:
x:
[[1. 1. 1. 1.]
[2. 2. 2. 2.]]
y:
[[2. 2.5 3. 3.5]
[2. 2.5 3. 3.5]]
x.ravel():
[1. 1. 1. 1. 2. 2. 2. 2.]
y.ravel():
[2. 2.5 3. 3.5 2. 2.5 3. 3.5]
grid:
[[1. 2. ]
[1. 2.5]
[1. 3. ]
[1. 3.5]
[2. 2. ]
[2. 2.5]
[2. 3. ]
[2. 3.5]]
2.2 神经网络复杂度
NN复杂度: 多用NN层数和NN参数的个数表示。
- 时间复杂度:
层数 = 隐藏层的层数 + 1个输出层 共2层NN
注:输入层仅传输数据,没有运算,所以不算入层数。
总参数 = 总权重数(w) + 总偏置数(b)
下图 3x4+4 + 4x2+2共 26 个参数
第1层 第2层 - 空间复杂度: 乘加运算次数,即神经网络中神经元连接线的条数。
下图 3x4 + 4x2 = 20
第1层 第2层

2.3 指数衰减学习率
上一讲对学习率的概念进行了介绍,本讲将对实际使用中的学习率(指数衰减学习率)设置进行讲解。
指数衰减学习率:
在实际训练过程中,可以先用较大的学习率,快速得到较优解,然后逐步减小学习率,使模型在训练后期稳定。 指 数 衰 减 学 习 率 = 初 始 学 习 率 ∗ 学 习 率 衰 减 率 ( 当 前 轮 数 / 多 少 轮 衰 减 一 次 ) 指数衰减学习率 = 初始学习率 * 学习率衰减率^{(当前轮数 / 多少轮衰减一次)} 指数衰减学习率=初始学习率∗学习率衰减率(当前轮数/多少轮衰减一次)其中,初始学习率、学习率衰减率、多少轮衰减一次为超参数;(当前轮数 / 多少轮衰减一次)使用整型数据类型,计算结果为整数。
2.4 激活函数
多层线性神经元组成的神经网络依旧为线性模型。激活函数的使用是为了实现神经网络的去线性化。
优秀的激活函数:
• 非线性: 激活函数非线性时,多层神经网络可逼近所有函数。
• 可微性: 优化器大多用梯度下降更新参数。
• 单调性: 当激活函数是单调的,能保证单层网络的损失函数是凸函数。
• 近似恒等性: f ( x ) ≈ x f(x)≈x f(x)≈x 当参数初始化为随机小值时,神经网络更稳定。
激活函数输出值的范围:
• 激活函数输出为有限值时,权重对输出的影响更显著,基于梯度的优化方法更稳定。
• 激活函数输出为无限值时,参数的初始值对模型的影响非常大,建议调小学习率。
常用的激活函数
Sigmoid激活函数
Sigmoid函数: f ( x ) = 1 1 + e − x f(x)=\frac{1}{1+e^{-x}} f(x)=1+e−x1
API:tf.nn. sigmoid(x)
Sigmoid函数特点:
(1)易造成梯度消失
(2)输出非0均值,收敛慢
(3)Sigmoid函数中存在复杂的幂运算 e − x e^{-x} e−x ,训练时间长。
Sigmoid函数相当于对输入进行了归一化,神经网络最初兴起时,sigmoid激活函数使用的较多。但是,近年来,sigmoid激活函数使用的较少,因为深层神经网络更新参数时,需要从输出层到输入层逐层进行链式求导,而sigmoid函数求导结果区间为 ( 0 , 0.25 ] (0,0.25] (0,0.25] ,这就导致了多层求导时,有多个 ( 0 , 0.25 ] (0,0.25] (0,0.25] 小数连续相乘,使得梯度趋近于 0 0 0 从而导致梯度消失。
此外,我们希望输入每层神经网络的特征为以 0 0 0 为均值的小数值,但是,Sigmoid函数的输出均为正数,会使收敛变慢。
![]()
Tanh激活函数
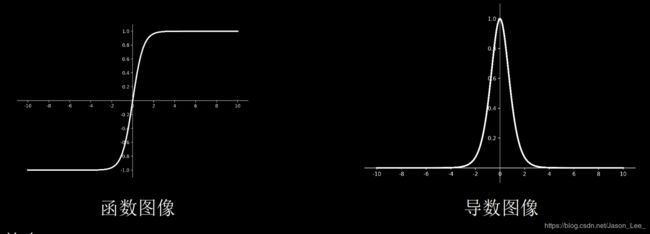
Tanh函数: f ( x ) = 1 − e − 2 x 1 + e − 2 x f(x)=\frac{1-e^{-2x}}{1+e^{-2x}} f(x)=1+e−2x1−e−2x
API: tf.math.tanh(x)
Tanh函数特点:
(1)比sigmoid函数收敛速度更快。
(2)输出是0均值
(3)易造成梯度消失
(4)幂运算复杂,训练时间长
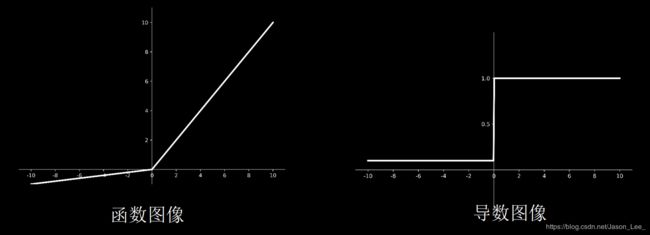
Relu激活函数
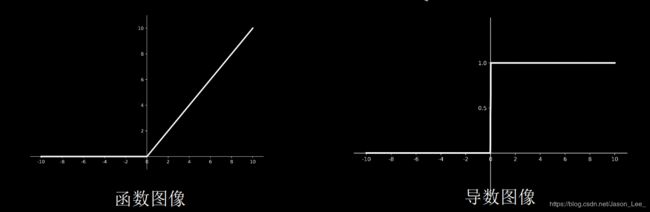
Relu函数: f ( x ) = max ( x , 0 ) = { 0 x < 0 x x ⩾ 0 f(x)=\text{max}(x,0)= \begin{cases} 0 &x<0 \\ x &x\geqslant 0 \end{cases} f(x)=max(x,0)={0xx<0x⩾0
API: tf.nn.relu(x)
Relu函数特点:
- 优点:
(1)解决了梯度消失问题(在正区间);
(2)只需判断输入是否大于0,计算速度快;
(3)收敛速度远快于sigmoid和tanh;
(4)提供了神经网络的稀疏表达能力。 - 缺点:
(1)输出非0均值,会使收敛变慢;
(2)Dead Relu问题:神经元输入为负数时,Relu输出为0,反向传播得到的梯度为零。使得某些神经元可能永远不会被激活,导致相应的参数永远不能被更新。这一点可以通过: 1) 改进随机初始化,避免初始化时过多的负数特征送入Relu函数;2) 可以通过设置更小的学习率,减少参数分布的巨大变化,避免训练过程中过多负数特征进入Relu函数。
Leaky Relu激活函数
Leaky Relu函数: f ( x ) = max ( α x , x ) f(x)=\text{max}(\alpha x,x) f(x)=max(αx,x)
API:tf.nn.leaky_relu(x)
Leaky Relu函数特点:
理论上来讲, Leaky Relu有Relu的所有优点,外加不会有Dead Relu问题,但是在实际操作当中,并没有完全证明Leaky Relu总是好于Relu。
初学者激活函数选择
- 首选relu激活函数;
- 学习率设置较小值;
- 输入特征标准化,即让输入特征满足以0为均值,1为标准差的正态分布;
- 初始参数中心化,即让随机生成的参数满足以0为均值, 2 当 前 层 输 入 特 征 个 数 \sqrt{\frac{2}{当前层输入特征个数}} 当前层输入特征个数2为标准差的正态分布。
2.5 损失函数
神经网络模型的效果及优化的目标是通过损失函数来定义的。回归和分类是监督学习中的两个大类。
损失函数(Loss):预测值( y ′ y' y′)与标准答案( y y y)的差距。
均方误差(Mean Square Error, MSE)损失函数
均方误差(Mean Square Error, MSE)是回归问题最常用的损失函数。 回归问题解决的是对具体数值的预测,比如房价预测、销量预测等。这些问题需要预测的不是一个事先定义好的类别,而是一个任意实数。均方误差定义如下: M S E ( y , y ′ ) = ∑ i = 1 n ( y i − y i ′ ) 2 n MSE(y,y')=\frac{\sum_{i=1}^n(y_i-y_i')^2}{n} MSE(y,y′)=n∑i=1n(yi−yi′)2其中 y i y_i yi 为一个batch中第i个数据的真实值,而 y i ′ y_i' yi′ 为神经网络的预测值。
API:
tf.keras.losses.MSE
loss_mse = tf.reduce_mean(tf.square(y_ - y))
自定义损失函数
均方误差损失函数在实际使用中存在一些限制和不足。例如,用于预测商品销量时,预测多了,损失成本;预测少了,损失利润。若利润 ≠ 成本,则MSE产生的Loss无法利益最大化。
自定义损失函数: l o s s ( y , y ′ ) = ∑ n f ( y , y ′ ) loss(y,y')=\sum_nf(y,y') loss(y,y′)=n∑f(y,y′)其中, y y y表示真实值, y ′ y' y′表示预测值。
针对商品销量预测问题,提出下述自定义损失函数:
f ( y , y ′ ) = { profit ∗ ( y − y ′ ) y ′ < y ; ( 预 测 少 了 , 损 失 利 润 ) cost ∗ ( y ′ − y ) y ′ > y ; ( 预 测 多 了 , 损 失 成 本 ) f(y,y')= \begin{cases} \text{profit}*(y-y') &y'
Tensorflow实现上述自定义损失函数:
# y: 真实值;y_: 预测值;
cost = 1
profit = 99
loss = tf.reduce_sum(tf.where(tf.greater(y, y_), profit * (y - y_), cost(y_-y)))
交叉熵(Cross Entropy, CE)损失函数
交叉熵损失函数 (Cross Entropy, CE):表征两个概率分布之间的距离。交叉熵越大,两个概率分布越远;交叉熵越小,两个概率分布越近。交叉熵损失函数定义如下: H ( P , Q ) = − ∑ P ( x ) ∗ ln Q ( x ) H(P,Q)=-\sum P(x)*\text{ln}Q(x) H(P,Q)=−∑P(x)∗lnQ(x)其中, P ( x ) , Q ( x ) P(x),Q(x) P(x),Q(x)为两个概率分布。注意, H ( P , Q ) ≠ H ( Q , P ) H(P,Q)\not =H(Q,P) H(P,Q)=H(Q,P)。
将概率分布 P P P 替换为实际分布 y y y , Q Q Q 替换为预测分布 y ′ y' y′。即可得到交叉熵损失函数
H ( y , y ′ ) = − ∑ y ∗ ln y ′ H(y,y')=-\sum y*\text{ln}y' H(y,y′)=−∑y∗lny′
API: tf.losses.categorical_crossentropy(y, y_)
Softmax与交叉熵
在实际使用中,通常先将网络输出通过一个Softmax函数,使网络输出符合概率分布,然后在计算交叉熵损失函数。
API: tf.nn.softmax_cross_entropy_with_logits(y, y_) # 该API结合了 Softmax 函数与交叉熵损失函数。
y = np.array([[1, 0, 0], [0, 1, 0], [0, 0, 1], [1, 0, 0], [0, 1, 0]]) # 标准答案
y_ = np.array([[12, 3, 2], [3, 10, 1], [1, 2, 5], [4, 6.5, 1.2], [3, 6, 1]]) # 预测结果
y_pro = tf.nn.softmax(y) # softmax函数
loss_ce1 = tf.losses.categorical_crossentropy(y_, y_pro) # 交叉熵损失函数
# loss_ce2 功能相当于上述两行之和
loss_ce2 = tf.nn.softmax_cross_entropy_with_logits(y_, y)
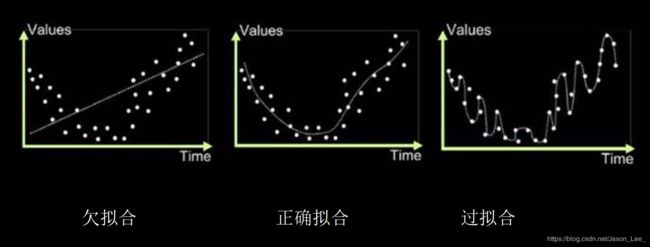
2.6 欠拟合与过拟合
- 欠拟合的解决方法:
增加输入特征项;
增加网络参数;
减少正则化参数。 - 过拟合的解决方法:
数据清洗,减少数据集中的噪声,使数据集更加纯净;
增大训练集,使得模型从更多数据中学习特征;
采用正则化;
增大正则化参数。
正则化(Regularization)缓解过拟合
正则化(Regularization)是一种缓解过拟合的通用的、有效的的方法。
正则化在损失函数中引入模型复杂度指标,利用给参数 W 加权值,弱化了训练数据的噪声(一般不正则化偏置项 b)。
使用正则化后的损失函数: L o s s = l o s s ( y , y ′ ) + R e g u l a r i z e r ∗ l o s s ( W ) Loss = loss(y, y') + Regularizer*loss(W) Loss=loss(y,y′)+Regularizer∗loss(W)其中, l o s s ( y , y ′ ) loss(y,y') loss(y,y′) 为模型中所有参数的损失函数,如:交叉熵、均方误差; R e g u l a r i z e r Regularizer Regularizer指用超参数 Regularizer 给出参数 W W W 在总 L o s s Loss Loss 中的比例,即正则化的权重; W W W为需要正则化的参数。
l o s s ( W ) loss(W) loss(W)的计算有两种方法: l o s s L 1 ( w ) = ∑ i ∥ w i ∥ L 1 正 则 化 l o s s L 2 ( w ) = ∑ i ∥ w i ∥ 2 L 2 正 则 化 \begin{aligned} &loss_{L1}(w)=\sum_i{\|w_i\|} &L1正则化\\ &loss_{L2}(w)=\sum_i{\|w_i\|^2} &L2正则化 \end{aligned} lossL1(w)=i∑∥wi∥lossL2(w)=i∑∥wi∥2L1正则化L2正则化L1正则化大概率会使很多参数变为零,因此该方法可通过稀疏参数,即减少参数的数量,降低复杂度。
L2正则化会使参数很接近零但不为零,因此该方法可通过减小参数值的大小,可有效缓解数据集中因噪声引起的过拟合,降低模型复杂度。
L2正则化计算 l o s s ( W ) loss(W) loss(W) 的过程:
with tf.GradientTape() as tape: # 记录梯度信息
h1 = tf.matmul(x_train, w1) + b1 # 记录神经网络乘加运算
h1 = tf.nn.relu(h1)
y = tf.matmul(h1, w2) + b2
# 采用均方误差损失函数mse = mean(sum(y-y')^2)
loss_mse = tf.reduce_mean(tf.square(y_train - y))
# 添加l2正则化
loss_regularization = []
# tf.nn.l2_loss(w)=sum(w ** 2) / 2
loss_regularization.append(tf.nn.l2_loss(w1))
loss_regularization.append(tf.nn.l2_loss(w2))
# 求和:
# 例:x=tf.constant(([1,1,1],[1,1,1]))
# tf.reduce_sum(x)
# >>>6
loss_regularization = tf.reduce_sum(loss_regularization)
loss = loss_mse + 0.03 * loss_regularization # REGULARIZER = 0.03
# 计算loss对各个参数的梯度
variables = [w1, b1, w2, b2]
grads = tape.gradient(loss, variables)
使用L2正则化与不适用L2正则化效果对比:
对下表中的数据进行分类预测:
源码:p29_regularizationfree.py p29_regularizationcontain.py
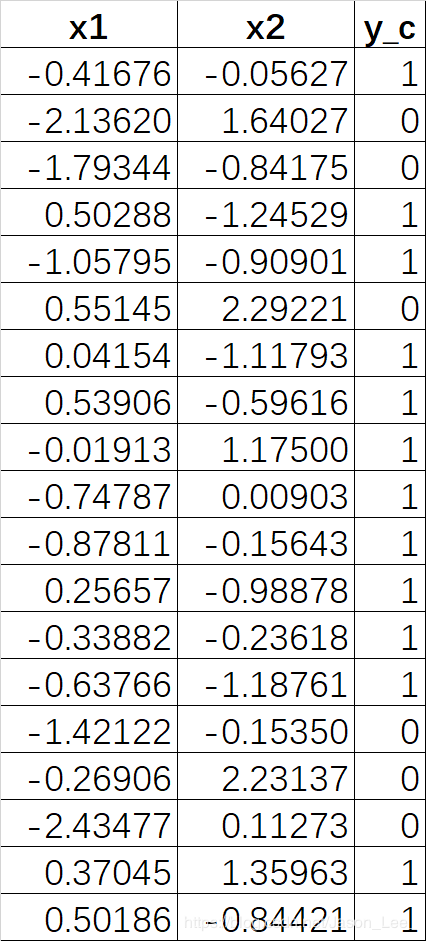
不使用L2正则化:
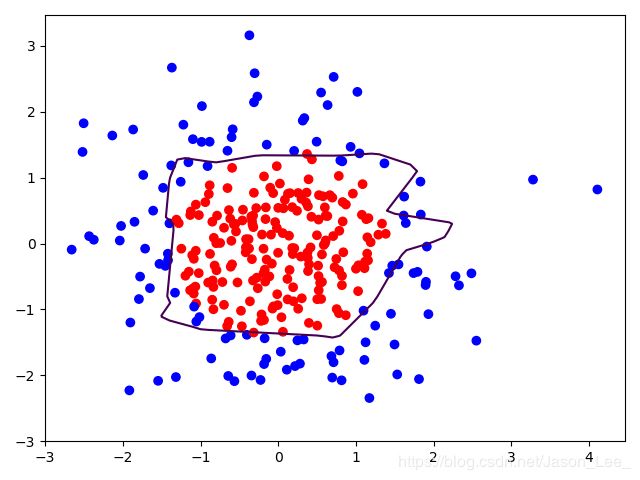 使用L2正则化:
使用L2正则化:
 可见,使用L2正则化的你和曲线更加平滑,L2正则化缓解了过拟合现象。
可见,使用L2正则化的你和曲线更加平滑,L2正则化缓解了过拟合现象。
2.7 神经网络参数优化器
神经网络是基于连接的人工智能,当神经网络结构固定后,不同参数的选取对模型的表达力影响很大。模型参数更新的过程,就相当于模型在学习新事物的过程。
就比如,更新模型参数的过程,就好像教一个孩子理解世界的过程,达到学龄的孩子,脑神经元的结构、规模是相似的,他们都具备了学习的潜力,但是不同的引导方法,会让孩子具备不同的能力,达到不同的高度。优化器就好比是引导神经网络更新参数的工具。
准备知识 待优化参数 w w w,损失函数 l o s s loss loss,学习率 l r lr lr;批batch
优化算法可以分成一阶优化和二阶优化算法,其中一阶优化就是指的梯度算法及其变种,而二阶优化一般是用二阶导数(Hessian 矩阵)来计算,如牛顿法,由于需要计算Hessian阵和其逆矩阵,计算量较大,因此没有流行开来。这里主要总结一阶优化的各种梯度下降方法。
深度学习优化算法经历了SGD -> SGDM -> NAG ->AdaGrad -> AdaDelta -> Adam -> Nadam这样的发展历程。
首先,明确几个关键符号: 待优化参数 w w w,损失函数 l o s s loss loss,学习率 l r lr lr;为提高效率,每次迭代一个batch,batch通常取值为 2 n 2^n 2n,用 t t t 表示当前batch迭代的总次数。
关于batch设置:
- batch通常取值为 2 n 2^n 2n;
- 当网络规模较大时,可以适当调整 batch_size 大小,使得训练时一次送入神经网络的数据量多一些;以充分发挥显卡的性能,提高训练速度,可以根据电脑的性能调节batch_size的数值,一般占据显卡70-80%的 负荷比较合理。
参数更新分为4个步骤:
- 计算 t t t 时刻损失函数 l o s s loss loss 关于当前参数 w t w_t wt 的梯度: g t = ∇ l o s s = ∂ l o s s ∂ w t g_t=\nabla loss=\frac{\partial{loss}}{\partial{w_t}} gt=∇loss=∂wt∂loss;
- 计算 t t t 时刻的 一阶动量 m t m_t mt 和 二阶动量 V t V_t Vt,不同的优化器实质上只是定义了不同的 一阶动量 和 二阶动量 公式;
- 计算 t t t 时刻下降梯度: η t = l r ∗ m t V t \eta_t=lr*\frac{m_t}{\sqrt{V_t}} ηt=lr∗Vtmt;
- 计算 t + 1 t+1 t+1 时刻的参数: w t + 1 = w t − η t = w t − l r ∗ m t V t w_{t+1}=w_t-\eta_t=w_t-lr*\frac{m_t}{\sqrt{V_t}} wt+1=wt−ηt=wt−lr∗Vtmt。
不同的优化器算法,步骤3,4都是一致的,主要差别体现在步骤1和2上。
随机梯度下降(stochastic gradient descent,SGD)
SGD: 不含动量(momentum)时,常用的梯度下降法。
API: tf.keras.optimizers.SGD
SGD算法一二阶动量定义为: m t = g t V t = 1 \begin{aligned} &m_t=g_t \\ &V_t=1 \end{aligned} mt=gtVt=1由此实现步骤3,4: η t = l r ∗ m t V t = l r ∗ g t w t + 1 = w t − η t = w t − l r ∗ m t V t = w t − l r ∗ g t \begin{aligned} &\eta_t=lr*\frac{m_t}{\sqrt{V_t}}=lr*g_t \\ &w_{t+1}=w_t-\eta_t=w_t-lr*\frac{m_t}{\sqrt{V_t}}=w_t-lr*g_t \end{aligned} ηt=lr∗Vtmt=lr∗gtwt+1=wt−ηt=wt−lr∗Vtmt=wt−lr∗gt所以,SGD算法的参数更新公式为: w t + 1 = w t − l r ∗ ∂ l o s s ∂ w t w_{t+1}=w_t-lr*\frac{\partial{loss}}{\partial{w_t}} wt+1=wt−lr∗∂wt∂loss
对于一层网络,实现SGD算法只需要两行代码:
# 实现梯度更新 w1 = w1 - lr * w1_grad b = b - lr * b_grad
w1.assign_sub(lr * grads[0]) # 参数w1自更新
b1.assign_sub(lr * grads[1]) # 参数b自更新
含动量的随机梯度下降(SGD + the first-order Momentum,SGDM)
SGDM为在SGD的基础上增加了一阶动量。
SGDM算法一二阶动量定义为: m t = β ∗ m t − 1 + ( 1 − β ) ∗ g t V t = 1 \begin{aligned} &m_t=\beta*m_{t-1}+(1-\beta)*g_t \\ &V_t=1 \end{aligned} mt=β∗mt−1+(1−β)∗gtVt=1即将一阶动量定义为各时刻梯度方向的指数滑动平均值。其中, β \beta β为一个超参数,是一个接近1的值, 经验值为0.9。由此实现步骤3,4: η t = l r ∗ m t V t = l r ∗ m t = l r ∗ ( β ∗ m t − 1 + ( 1 − β ) ∗ g t ) w t + 1 = w t − η t = w t − l r ∗ ( β ∗ m t − 1 + ( 1 − β ) ∗ g t ) \begin{aligned} &\eta_t=lr*\frac{m_t}{\sqrt{V_t}}=lr*m_t=lr*(\beta*m_{t-1}+(1-\beta)*g_t) \\ &w_{t+1}=w_t-\eta_t=w_t-lr*(\beta*m_{t-1}+(1-\beta)*g_t) \end{aligned} ηt=lr∗Vtmt=lr∗mt=lr∗(β∗mt−1+(1−β)∗gt)wt+1=wt−ηt=wt−lr∗(β∗mt−1+(1−β)∗gt)所以,SGDM算法的参数更新公式为: w t + 1 = w t − l r ∗ ( β ∗ m t − 1 + ( 1 − β ) ∗ g t ) w_{t+1}=w_t-lr*(\beta*m_{t-1}+(1-\beta)*g_t) wt+1=wt−lr∗(β∗mt−1+(1−β)∗gt)
SGDM算法实现:
m_w, m_b = 0, 0 # 初始时刻 (t=0) 的一阶动量为0
beta = 0.9
m_w = beta * m_w + (1 - beta) * grads[0]
m_b = beta * m_b + (1 - beta) * grads[1]
w1.assign_sub(lr * m_w)
b1.assign_sub(lr * m_b)
Adagrad(SGD + the second-order Momentum)
Adagrad是在SGD的基础上增加二阶动量。
Adagrad算法一二阶动量定义为: m t = g t V t = ∑ τ = 1 t g τ 2 \begin{aligned} &m_t=g_t \\ &V_t=\sum_{\tau=1}^t g_\tau^2 \end{aligned} mt=gtVt=τ=1∑tgτ2由此实现步骤3,4: η t = l r ∗ m t V t = l r ∗ g t ∑ τ = 1 t g τ 2 w t + 1 = w t − η t = w t − l r ∗ g t ∑ τ = 1 t g τ 2 \begin{aligned} &\eta_t=lr*\frac{m_t}{\sqrt{V_t}}=lr*\frac{g_t}{\sqrt{\sum_{\tau=1}^t g_\tau^2}} \\ &w_{t+1}=w_t-\eta_t=w_t-lr*\frac{g_t}{\sqrt{\sum_{\tau=1}^t g_\tau^2}} \end{aligned} ηt=lr∗Vtmt=lr∗∑τ=1tgτ2gtwt+1=wt−ηt=wt−lr∗∑τ=1tgτ2gt所以,Adagrad算法的参数更新公式为: w t + 1 = w t − l r ∗ g t ∑ τ = 1 t g τ 2 w_{t+1}=w_t-lr*\frac{g_t}{\sqrt{\sum_{\tau=1}^t g_\tau^2}} wt+1=wt−lr∗∑τ=1tgτ2gt
Adagrad算法实现:
v_w, v_b = 0, 0 # 初始时刻 (t=0) 二阶动量为0
# adagrad
v_w += tf.square(grads[0])
v_b += tf.square(grads[1])
w1.assign_sub(lr * grads[0] / tf.sqrt(v_w))
b1.assign_sub(lr * grads[1] / tf.sqrt(v_b))
RMSProp(SGD + the second-order Momentum)
RMSProp是在SGD基础上增加二阶动量。
RMSProp算法一二阶动量定义为: m t = g t V t = β ∗ V t − 1 + ( 1 − β ) ∗ g t 2 \begin{aligned} &m_t=g_t \\ &V_t=\beta*V_{t-1}+(1-\beta)*g_t^2 \end{aligned} mt=gtVt=β∗Vt−1+(1−β)∗gt2二阶动量 V V V 使用指数滑动平均值计算,表征的是过去一段时间的平均值。由此实现步骤3,4: η t = l r ∗ m t V t = l r ∗ g t β ∗ V t − 1 + ( 1 − β ) ∗ g t 2 w t + 1 = w t − η t = w t − l r ∗ g t β ∗ V t − 1 + ( 1 − β ) ∗ g t 2 \begin{aligned} &\eta_t=lr*\frac{m_t}{\sqrt{V_t}}=lr*\frac{g_t}{\sqrt{\beta*V_{t-1}+(1-\beta)*g_t^2}} \\ &w_{t+1}=w_t-\eta_t=w_t-lr*\frac{g_t}{\sqrt{\beta*V_{t-1}+(1-\beta)*g_t^2}} \end{aligned} ηt=lr∗Vtmt=lr∗β∗Vt−1+(1−β)∗gt2gtwt+1=wt−ηt=wt−lr∗β∗Vt−1+(1−β)∗gt2gt所以,RMSProp算法的参数更新公式为: w t + 1 = w t − l r ∗ g t β ∗ V t − 1 + ( 1 − β ) ∗ g t 2 w_{t+1}=w_t-lr*\frac{g_t}{\sqrt{\beta*V_{t-1}+(1-\beta)*g_t^2}} wt+1=wt−lr∗β∗Vt−1+(1−β)∗gt2gt
RMSProp算法实现:
v_w, v_b = 0, 0 # 初始时刻 (t=0) 二阶动量为0
beta = 0.9
# rmsprop
v_w = beta * v_w + (1 - beta) * tf.square(grads[0])
v_b = beta * v_b + (1 - beta) * tf.square(grads[1])
w1.assign_sub(lr * grads[0] / tf.sqrt(v_w))
b1.assign_sub(lr * grads[1] / tf.sqrt(v_b))
设置 l r = 0.1 , e p o c h = 500 , b a t c h = 32 lr=0.1, epoch=500, batch=32 lr=0.1,epoch=500,batch=32 ,结果:
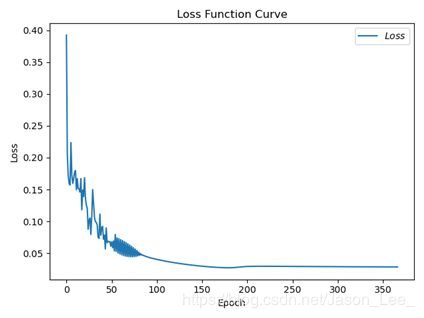
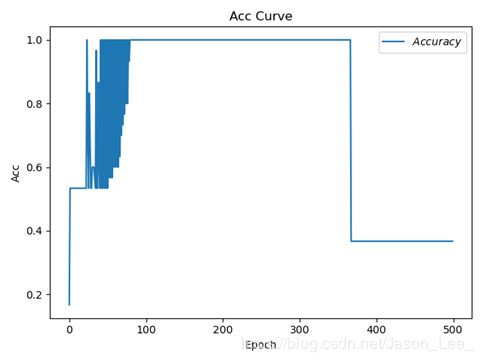
结果出现震荡,调小学习率可以解决这个问题,设置 l r = 0.01 , e p o c h = 100 , b a t c h = 32 lr=0.01, epoch=100, batch=32 lr=0.01,epoch=100,batch=32 ,结果:
Adam(SGD + the first-order Momentum + the second-order Momentum)
Adam算法同时结合SGDM一阶动量和RMSProp二阶动量,并在此基础上增加了两个修正项。
Adam算法一二阶动量定义为: m t = β 1 ∗ m t − 1 + ( 1 − β 1 ) ∗ g t 修 正 一 阶 动 量 的 偏 差 : m t ^ = m t 1 − β 1 t V t = β 2 ∗ V t − 1 + ( 1 − β 2 ) ∗ g t 2 正 二 阶 动 量 的 偏 差 : V t ^ = V t 1 − β 2 t \begin{aligned} &m_t=\beta_1*m_{t-1}+(1-\beta_1)*g_t &&修正一阶动量的偏差:\widehat{m_t}=\frac{m_t}{1-\beta_1^t}\\ &V_t=\beta_2*V_{t-1}+(1-\beta_2)*g_t^2 &&正二阶动量的偏差:\widehat{V_t}=\frac{V_t}{1-\beta_2^t} \end{aligned} mt=β1∗mt−1+(1−β1)∗gtVt=β2∗Vt−1+(1−β2)∗gt2修正一阶动量的偏差:mt =1−β1tmt正二阶动量的偏差:Vt =1−β2tVt将修正后的一阶动量和二阶动量带入步骤3,4进行参数更新: η t = l r ∗ m t ^ V t ^ = l r ∗ ( m t 1 − β 1 t / V t 1 − β 2 t ) w t + 1 = w t − η t = w t − l r ∗ ( m t 1 − β 1 t / V t 1 − β 2 t ) \begin{aligned} &\eta_t=lr*\frac{\widehat{m_t}}{\sqrt{\widehat{V_t}}}=lr*(\frac{m_t}{1-\beta_1^t}/\sqrt{\frac{V_t}{1-\beta_2^t}}) \\ &w_{t+1}=w_t-\eta_t=w_t-lr*(\frac{m_t}{1-\beta_1^t}/\sqrt{\frac{V_t}{1-\beta_2^t}}) \end{aligned} ηt=lr∗Vt mt =lr∗(1−β1tmt/1−β2tVt)wt+1=wt−ηt=wt−lr∗(1−β1tmt/1−β2tVt)所以,RMSProp算法的参数更新公式为: w t + 1 = w t − l r ∗ ( β 1 ∗ m t − 1 + ( 1 − β 1 ) ∗ g t 1 − β 1 t / β 2 ∗ V t − 1 + ( 1 − β 2 ) ∗ g t 2 1 − β 2 t ) w_{t+1}=w_t-lr*(\frac{\beta_1*m_{t-1}+(1-\beta_1)*g_t}{1-\beta_1^t}/\sqrt{\frac{\beta_2*V_{t-1}+(1-\beta_2)*g_t^2}{1-\beta_2^t}}) wt+1=wt−lr∗(1−β1tβ1∗mt−1+(1−β1)∗gt/1−β2tβ2∗Vt−1+(1−β2)∗gt2)
Adam算法实现:
m_w, m_b = 0, 0 # 初始时刻 (t=0) 一阶动量为0
v_w, v_b = 0, 0 # 初始时刻 (t=0) 二阶动量为0
beta1, beta2 = 0.9, 0.999
global_step = 0 # 从训练开始到当前时刻所经历的总batch数
# adam
m_w = beta1 * m_w + (1 - beta1) * grads[0]
m_b = beta1 * m_b + (1 - beta1) * grads[1]
v_w = beta2 * v_w + (1 - beta2) * tf.square(grads[0])
v_b = beta2 * v_b + (1 - beta2) * tf.square(grads[1])
m_w_correction = m_w / (1 - tf.pow(beta1, int(global_step)))
m_b_correction = m_b / (1 - tf.pow(beta1, int(global_step)))
v_w_correction = v_w / (1 - tf.pow(beta2, int(global_step)))
v_b_correction = v_b / (1 - tf.pow(beta2, int(global_step)))
w1.assign_sub(lr * m_w_correction / tf.sqrt(v_w_correction))
b1.assign_sub(lr * m_b_correction / tf.sqrt(v_b_correction))
优化器选择
很难说某一个优化器在所有情况下都表现很好,我们需要根据具体任务选取优化器。一些优化器在计算机视觉任务表现很好,另一些在涉及RNN网络时表现很好,甚至在稀疏数据情况下表现更出色。
总结上述,基于原始SGD增加动量和Nesterov动量,RMSProp是针对AdaGrad学习率衰减过快的改进,它与AdaDelta非常相似,不同的一点在于AdaDelta采用参数更新的均方根(RMS)作为分子。Adam在RMSProp的基础上增加动量和偏差修正。如果数据是稀疏的,建议用自适用方法,即Adagrad, RMSprop, Adadelta, Adam。RMSprop, Adadelta, Adam 在很多情况下的效果是相似的。随着梯度变的稀疏,Adam 比 RMSprop 效果会好。总的来说,Adam整体上是最好的选择。
然而很多论文仅使用不带动量的vanilla SGD和简单的学习率衰减策略。SGD通常能够达到最小点,但是相对于其他优化器可能要采用更长的时间。采取合适的初始化方法和学习率策略,SGD更加可靠,但也有可能陷于鞍点和极小值点。因此,当在训练大型的、复杂的深度神经网络时,我们想要快速收敛,应采用自适应学习率策略的优化器。
如果是刚入门,优先考虑Adam或者SGD+Nesterov Momentum。
算法没有好坏,最适合数据的才是最好的,永远记住:No free lunch theorem。
第三讲 神经网络八股
在前两讲中主要使用 TensorFlow2 的原生代码搭建神经网络。接下来将使用 Keras 搭建神经网络。Keras 可以看作是对 TensorFlow 进行封装的的高阶应用程序接口,可以快速搭建神经网络模型。TensorFlow 需要100多行实现的Iris数据集分类,使用 Keras 只需不到20行即可复现。
TensorFlow API: tf.keras
3.1 搭建网络八股 Sequential
神经网络搭建“六步法”
使用 tf.keras 通过 六步法 搭建神经网络:
- import
导入相关模块。 - train, test
确定要输入神经网络的训练集和测试集是什么,即指定训练集的输入特征 x_train 和 训练集标签 y_train,测试集的输入特征 x_test 和 测试集标签 y_test。 - model = tf.keras.models.Sequential
在 Sequential() 中搭建网络结构,逐层描述每层网络,相当于走了一遍前向传播。 - model.compile
在 compile() 中配置训练方法,告知训练时选择哪种优化器,选择哪个损失函数,选择哪种评测指标。 - model.fit
在 fit() 中执行训练过程,告知训练集和测试集的输入特征和标签,告知 batch 大小,告知迭代次数。 - model.summary
用 summary() 打印出网络的结构和参数统计。
将这 6 步作为编写神经网络代码的提纲,有迹可循。
接下来介绍 Sequential(),compile(),fit() 和 summary() 的用法。
Sequential()
Sequential() 可以认为是一个容器,这个容器里封装了一个神经网络结构。在Sequential中,要描述从输入层到输出层每一层的网络结构。 每一层的网络结构可以为以下几种类型:
- 拉直层:
tf.keras.layers.Flatten()
这一层不含计算,只是形状转换,将输入特征拉直变成一维数组。 - 全连接层:
tf.keras.layers.Dense(本层神经元个数, activation="激活函数“ , kernel_regularizer=哪种正则化)
activation= relu、softmax、sigmoid、tanh
kernel_regularizer= tf.keras.regularizers.l1()、 tf.keras.regularizers.l2() - 卷积层:
tf.keras.layers.Conv2D(filters=卷积核个数, kernel_size=卷积核尺寸, strides=卷积步长, padding="valid" or "same") - LSTM:
tf.keras.layers.LSTM()
compile()
compile() 配置神经网络的训练方法,在该部分,告知训练时选择的优化器、损失函数和评价指标。
API: model.compile(optimizer=优化器, loss=损失函数, metrics=[“准确率”] )
- optimizer=
‘sgd’ ortf.keras.optimizers.SGD (lr=学习率,momentum=动量参数)
‘adagrad’ ortf.keras.optimizers.Adagrad (lr=学习率)
‘adadelta’ ortf.keras.optimizers.Adadelta (lr=学习率)
‘adam’ ortf.keras.optimizers.Adam (lr=学习率, beta_1=0.9, beta_2=0.999)
优化器可以为以字符串形式给出的优化器名字,也可以为函数形式,使用函数形式可以设定学习率、动量等超参数。 - loss=
‘mse’ ortf.keras.losses.MeanSquaredError()
‘sparse_categorical_crossentropy’ ortf.keras.losses.SparseCategoricalCrossentropy(from_logits=False)
损失函数可以为以字符串形式给出的损失函数名字,也可以为函数形式。
在设置损失函数时,有一个参数 from_logits= 。有些神经网络的输出经过了 softmax 等函数,符合概率分布,有些则不以概率分布形式输出。这个参数则是在询问是否使用不经过softmax的原始输出。如果设置 from_logits=True ,则代表神经网络输出为未经过softmax的原始输出;如果设置 from_logits=False,则代表神经网络输出为经过了softmax的概率分布。
注:如果神经网络的预测概率和蒙的一样,比如十分类预测正确的概率为 1/10 ,很可能是这个参数设置错误。 - metrics=
‘accuracy’: y_truth 和 y_pred 都以数值形式给出,如y_truth=[1],y_pred=[1];
‘categorical_accuracy’: y_truth 和 y_pred 都以one-hot编码(概率分布)形式给出,如y_=[0,1,0],y=[0.256,0.695,0.048];
‘sparse_categorical_accuracy’: y_truth 是数值, y_pred 是独热码(概率分布),如y_=[1],y=[0.256,0.695,0.048]。
fit()
fit() 执行训练过程,
API:
# validation_data参数与validation_split参数二选一
model.fit (训练集的输入特征,
训练集的标签,
batch_size= ,
epochs= ,
validation_data=(验证集的输入特征,验证集的标签),
validation_split=从训练集划分多少比例给验证集,
validation_freq=经历多少次epoch使用验证集测试一次) # validation_fre不能大于训练epoch数
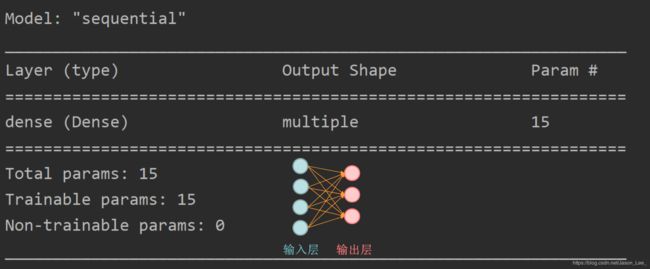
summary()
summary() 可以打印出网络的结构和参数统计。
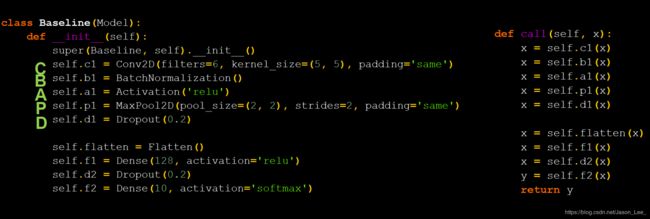
3.2 搭建网络八股 class
使用Sequential()方法可靠搭建出上层输出就是下层输入的顺序神经网络结构。但是,无法写出一些具有 跳跃连接 的非顺序网络结构,这时候我们可以选择用 类class 搭建神经网络结构。
可以使用 class类 封装一个神经网络结构。
from tensorflow.keras import Model
class MyModel(Model): # MyModel:搭建的神经网络名字,MyModel(Model)表示继承了TensorFlow的Model类
# __init__函数准备出搭建网络所需的各种“积木”
def __init__(self):
super(MyModel, self).__init__()
# 定义网络结构块
…………
# call函数调用__init__中的各种积木,实现前向传播
def call(self, x):
调用网络结构块,实现前向传播
return y
model = MyModel() # 利用类MyModel实例化出model对象
class IrisModel(Model):
def __init__(self):
super(IrisModel, self).__init__()
# d1为自定义的当前层的名字
self.d1 = Dense(3, activation='softmax', kernel_regularizer=tf.keras.regularizers.l2())
def call(self, x=None, **kwargs):
y = self.d1(x)
return y
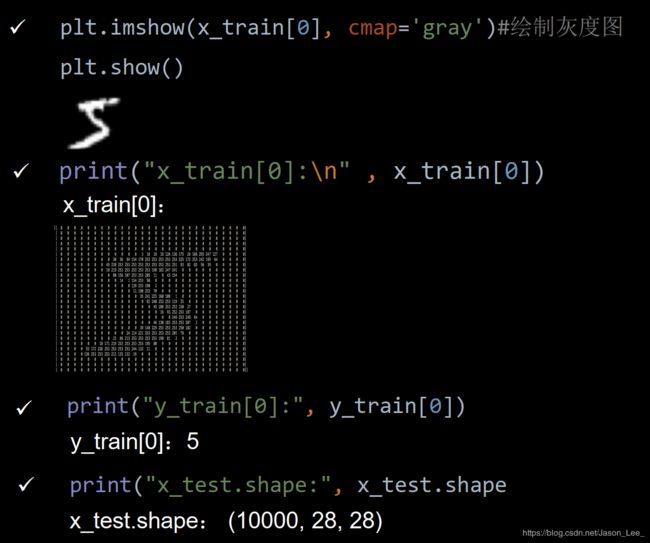
3.3 MNIST数据集
提供 6 万张 28 ∗ 28 28*28 28∗28 像素点的 0~9 手写数字图片和标签,用于训练。
提供 1 万张 28 ∗ 28 28*28 28∗28 像素点的 0~9 手写数字图片和标签,用于测试。
# 导入MNIST数据集:
mnist = tf.keras.datasets.mnist
# 分别导入训练集和验证集
(x_train, y_train), (x_test, y_test) = mnist.load_data()
# 对输入进行归一化,将输入值变小更适合神经网络吸收
x_train, x_test = x_train / 255.0, x_test / 255.0
全连接神经网络的输入为一个一维数组,所以需要将输入的 28 ∗ 28 28*28 28∗28 图片拉直成为一维数组。
# 拉直层
tf.keras.layers.Flatten()
3.4 FASHION数据集
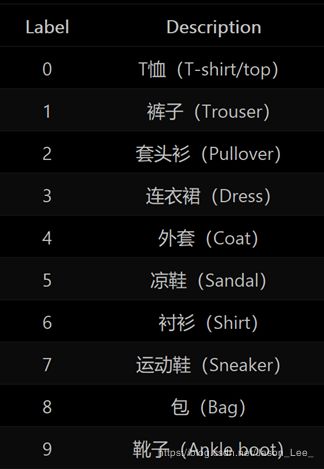
提供 6 万张 28 ∗ 28 28*28 28∗28 像素点的衣裤等图片和标签,用于训练。
提供 1 万张 28 ∗ 28 28*28 28∗28 像素点的衣裤等图片和标签,用于测试。
该数据集共包含十个类别的图片:
fashion = tf.keras.datasets.fashion_mnist
(x_train, y_train),(x_test, y_test) = fashion.load_data()
第四讲 神经网络八股扩展
在上一讲中介绍了使用 tf.keras 搭建神经网络的 “六步法”:
- import
- train, test
- model = tf.keras.models.Sequential / class
- model.compile
- model.fit
- model.summary
本讲将在“六步法”的基础上,进行扩展:
- 自建数据集
在之前的学习中,都是使用已经打包好的数据,使用.load_data方法来导入训练和验证数据。
使用 自建数据集 ,如何给 (x_train, y_train), (x_test, y_test) 赋值呢?
fashion = tf.keras.datasets.fashion_mnist
(x_train, y_train), (x_test, y_test) = fashion.load_data()
-
数据增强
如果训练数据不足,模型见识不足,模型的泛化能力会较弱。针对这一问题,还需要进行 数据增强 ,来扩展数据,提高泛化力。 -
断点续训
如果每次训练都从头开始,是一件很不划算的事,所以需要引入 断点续训 ,来实时保存最优模型。 -
参数提取
神经网络训练的目的,就是获取各层网络最优的参数。只要拿到这些参数,就能够在任何平台实现前向推断,复现出模型,实现应用。所以需要进行 参数提取 ,将参数存入文本。 -
acc & loss 可视化
由于tf.keras的高度封装,是我们不能像使用TensorFlow那样进行 acc & loss 曲线绘制,所以本讲将对使用tf.keras实现 acc & loss 可视化 进行讲解。 -
前向推理实现应用
模型训练好以后,输入神经网络一组新的/从未见过的特征,神经网络会输出预测的结果,实现学以致用。
- 本讲目标:
① 自制数据集,解决本领域应用
② 数据增强,扩充数据集
③ 断点续训,存取模型
④ 参数提取,把参数存入文本
⑤ acc/loss可视化,查看训练效果
⑥ 应用程序,给图识物
4.1 自建数据集
还是使用MNIST数据集进行练习,使用 .load_data 方法来导入训练和验证数据后各数据的尺寸为:

以自建数据集方式,编写函数,导入 (x_train, y_train), (x_test, y_test) :
def generate_datasets(path, txt):
f = open(txt, 'r') # 以只读形式打开txt文件
contents = f.readlines() # 读取文件中所有行
f.close() # 关闭txt文件
x, y_ = [], [] # 建立空列表
for content in contents: # 逐行取出
value = content.split() # 以空格分开,图片路径为value[0] , 标签为value[1] , 存入列表
img_path = path + value[0] # 拼出图片路径和文件名
img = Image.open(img_path) # 读入图片
img = np.array(img.convert('L')) # 图片变为8位宽灰度值的np.array格式
img = img / 255. # 数据归一化 (实现预处理)
x.append(img) # 归一化后的数据,贴到列表x
y_.append(value[1]) # 标签贴到列表y_
print('loading : ' + content) # 打印状态提示
x = np.array(x) # 变为np.array格式
y_ = np.array(y_) # 变为np.array格式
y_ = y_.astype(np.int64) # 变为64位整型
return x, y_ # 返回输入特征x,返回标签y_
if os.path.exists(x_train_savepath) and os.path.exists(y_train_savepath) and os.path.exists(
x_test_savepath) and os.path.exists(y_test_savepath):
print('-------------Load Datasets-----------------')
x_train_save = np.load(x_train_savepath)
y_train = np.load(y_train_savepath)
x_test_save = np.load(x_test_savepath)
y_test = np.load(y_test_savepath)
x_train = np.reshape(x_train_save, (len(x_train_save), 28, 28))
x_test = np.reshape(x_test_save, (len(x_test_save), 28, 28))
else:
print('-------------Generate Datasets-----------------')
x_train, y_train = generate_datasets(train_path, train_txt)
x_test, y_test = generate_datasets(test_path, test_txt)
print('-------------Save Datasets-----------------')
x_train_save = np.reshape(x_train, (len(x_train), -1)) # 将x_train由60000*28*28 reshape为60000*784
x_test_save = np.reshape(x_test, (len(x_test), -1)) # 将x_tset由60000*28*28 reshape为60000*784
np.save(x_train_savepath, x_train_save)
np.save(y_train_savepath, y_train)
np.save(x_test_savepath, x_test_save)
np.save(y_test_savepath, y_test)
4.2 数据增强
数据增强可以帮助扩展数据集,对图像进行数据增强就是对图像进行简单的形变。用来应对因拍照角度不同所引起的图像变形。
API:
from tensorflow.keras.preprocessing.image import ImageDataGenerator
image_gen_train = tf.keras.preprocessing.image.ImageDataGenerator(
rescale = 所有数据(像素值)将乘以该数值
rotation_range = 随机旋转角度数范围
width_shift_range = 随机宽度偏移量
height_shift_range = 随机高度偏移量
horizontal_flip = 是否随机水平翻转
zoom_range = 随机缩放的范围 [1-n, 1+n])
image_gen_train.fit(x_train)
举个栗子:
from tensorflow.keras.preprocessing.image import ImageDataGenerator
image_gen_train = ImageDataGenerator(
rescale=1. / 1., # 如为图像,分母为255时,可归至0~1
rotation_range=45, # 随机45度旋转
width_shift_range=.15, # 宽度偏移
height_shift_range=.15, # 高度偏移
horizontal_flip=False, # 水平翻转
zoom_range=0.5 # 将图像随机缩放阈量50%)
x_train = x_train.reshape(x_train.shape[0], 28, 28, 1) # 将x_train由60000*28*28 reshape为60000*28*28*1,其中的 *1 指单通道
image_gen_train.fit(x_train) # 对x_train进行数据增强操作
因为在 image_gen_train.fit() 中需要输入四维数组,所以需要对 x_train 进行 reshape 维度变换: ( 60000 , 28 , 28 ) ⟹ ( 60000 , 28 , 28 , 1 ) (60000, 28, 28)\Longrightarrow(60000, 28, 28, 1) (60000,28,28)⟹(60000,28,28,1)。model.fit() 也需要进行相应修改:
注意: 此处 image_gen_train.fit() 与 model.fit() 中的 .fit() 方法不是同一个方法,分别属于 ImageDataGenerator() 与 tf.keras.models.Sequential() 。
model.fit(x_train, y_train,batch_size=32, ……)
# 改为下面的形式执行训练过程: image_gen_train.flow(x_train, y_train,batch_size=32) 是以flow形式按照batch打包后执行训练过程
model.fit(image_gen_train.flow(x_train, y_train,batch_size=32), ……)
4.3 断点续训
断点续训可以存取模型(模型参数)。
保存模型
借助 tensorflow 给出的回调函数,在 fit() 中添加 callbacks=[] 参数,直接保存参数和网络。
API:
# monitor 配合 save_best_only 可以保存最优模型,包括:训练损失最小模型、测试损失最小模型、训练准确率最高模型、测试准确率最高模型等。
tf.keras.callbacks.ModelCheckpoint(filepath=路径+文件名,
save_weights_only=True/False, # 是否只保留模型参数
monitor='val_loss', # val_loss or loss
save_best_only=True/False) # 是否只保留最优结果
# 执行训练过程时,加入callbacks选项,记录到history中
# 之前使用 model.fit() 未记录到history中:
# model.fit(x_train, y_train, batch_size=32, epochs=5,
# validation_data=(x_test, y_test),
# validation_freq=1,
# callbacks=[cp_callback])
history = model.fit(x_train, y_train, batch_size=32, epochs=5,
validation_data=(x_test, y_test),
validation_freq=1,
callbacks=[cp_callback])
读取模型
模型读取可由TensorFlow给出的 .load_weights() 函数。
API: load_weights(路径文件名)
# 保存为 .ckpt 文件,因为保存为 .ckpt 文件时会同步生成索引表,通过判断是否存在索引表 .index ,就知道是否已经保存过模型参数了。
checkpoint_save_path = "./checkpoint/mnist.ckpt"
# 如果已经有了索引表,就可以直接读取模型参数
if os.path.exists(checkpoint_save_path + '.index'):
print('-------------load the model-----------------')
model.load_weights(checkpoint_save_path)
4.4 参数提取
实现参数提取,将参数存入文本文件。
TensorFlow API: model.trainable_variables 返回模型中可训练的参数。
可以直接使用print输出这些参数,但是,直接print,会有大量的数据输出用省略号替换掉。所以需要设置print()函数的打印效果:np.set_printoptions(threshold=超过多少省略显示)。
np.set_printoptions(threshold=np.inf) # np.inf表示无限大
print(model.trainable_variables)
# 将参数写入文本文件
file = open('./weights.txt', 'w')
for v in model.trainable_variables:
file.write(str(v.name) + '\n')
file.write(str(v.shape) + '\n')
file.write(str(v.numpy()) + '\n')
file.close()
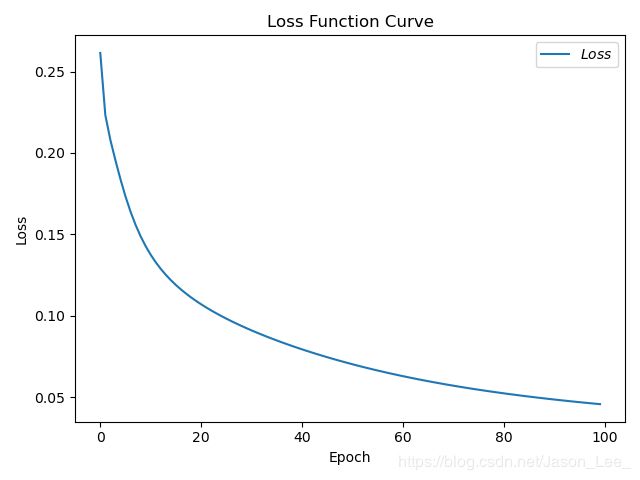
4.5 acc & loss 可视化
将模型训练过程中,准确率上升,损失函数下降的过程可视化出来。
history=model.fit(训练集数据, 训练集标签, batch_size=, epochs=,
validation_split=用作测试数据的比例,
validation_data=测试集,
validation_freq=测试频率)
在 model.fit() 执行训练过程时,同步记录了:
- 训练集loss:loss
- 测试集loss:val_loss
- 训练集准确率:sparse_categorical_accuracy
- 测试集准确率:val_sparse_categorical_accuracy
可以使用history.history[]提取出来。
acc = history.history['sparse_categorical_accuracy']
val_acc = history.history['val_sparse_categorical_accuracy']
loss = history.history['loss']
val_loss = history.history['val_loss']
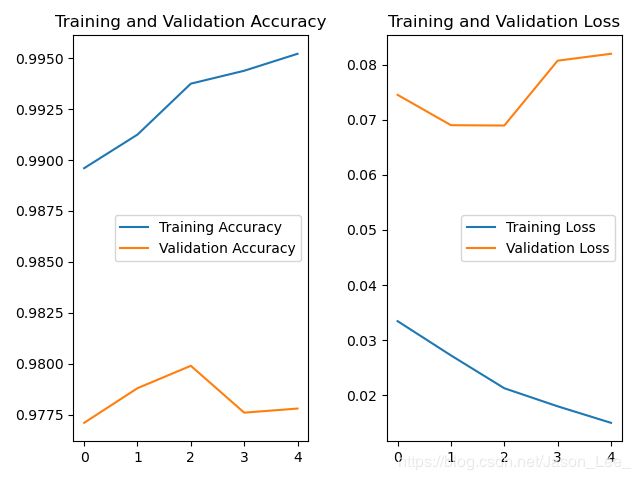
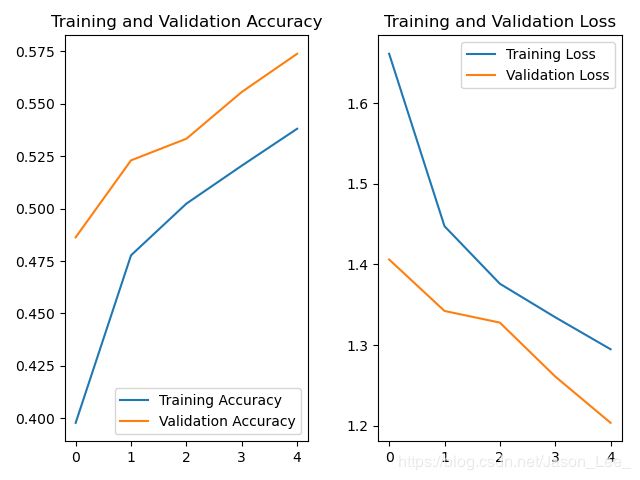
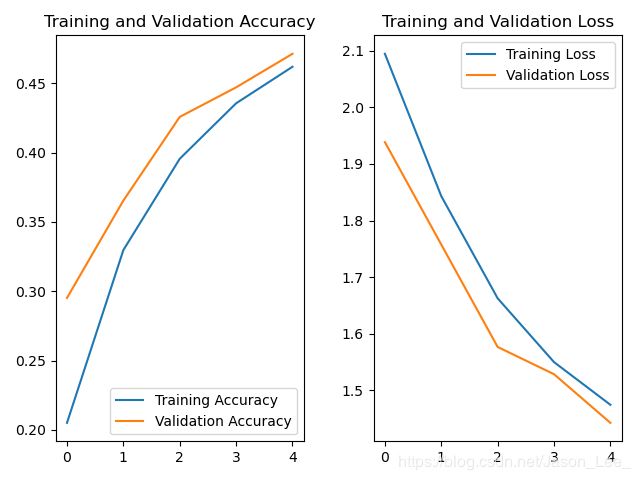
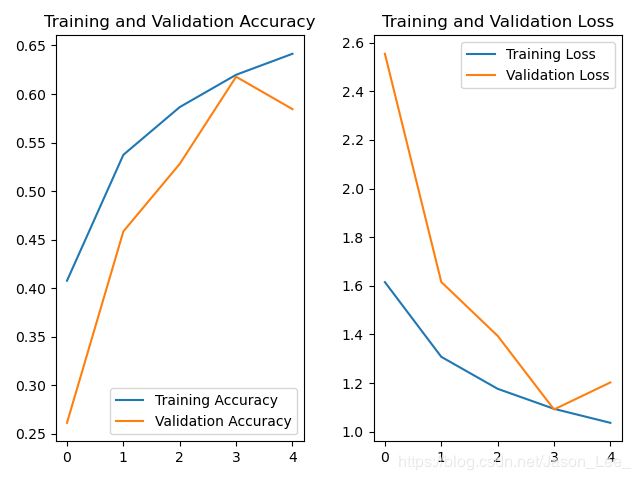
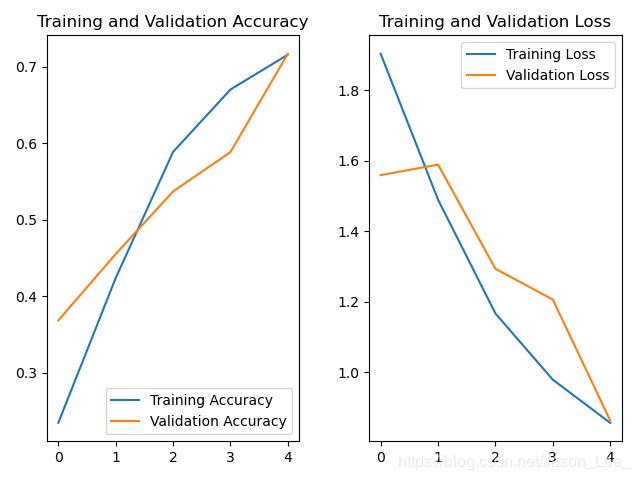
将 acc & loss 曲线绘制出来:
plt.subplot(1, 2, 1)
plt.plot(acc, label='Training Accuracy')
plt.plot(val_acc, label='Validation Accuracy')
plt.title('Training and Validation Accuracy')
plt.legend()
plt.subplot(1, 2, 2)
plt.plot(loss, label='Training Loss')
plt.plot(val_loss, label='Validation Loss')
plt.title('Training and Validation Loss')
plt.legend()
plt.show()
4.6 应用程序:给图识物
要让训练的神经网络模型可用,就需要编写一套应用程序,实现给图识物。
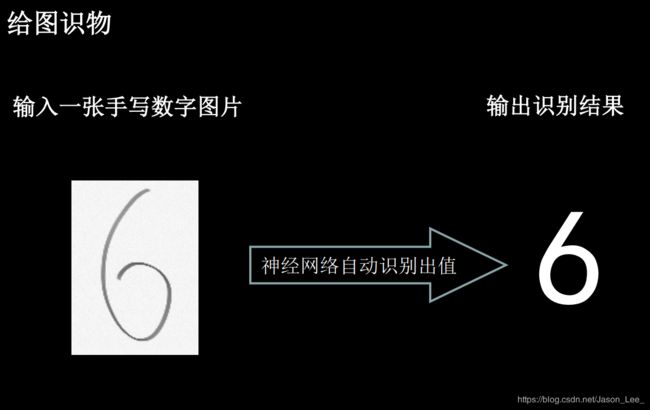
TensorFlow给出了 predict() 函数,可以实现根据输入特征输出预测结果。在 predict() 基础上实现前向传播执行识图应用只需要三步:
# 复现模型(前向传播)搭建网络框架
model = tf.keras.models.Sequential([tf.keras.layers.Flatten(),
tf.keras.layers.Dense(128, activation='relu'),
tf.keras.layers.Dense(10, activation='softmax’)])
# 加载参数
model.load_weights(model_save_path)
# 预测结果
result = model.predict(x_predict)
注意: 模型应用需要对输入待预测数据进行预处理。
- 在训练模型时使用的是 28 ∗ 28 28*28 28∗28 的灰度图。所以在应用时需要先将输入resize成 28 ∗ 28 28*28 28∗28 的标准尺寸,并转换为灰度图。
- 也可以将图片二值化输入,这样不仅保留了图片有用信息,而且滤去了背景噪声,选择合适的二值化阈值,识别效果会更好。
- 此外还需要注意,训练时使用的图片为黑底白字,所以应用时需要将白底黑字的图片转换成为黑底白字的图片,即
img_arr = 255 - img_arr实现颜色取反。 - 神经网络训练时都是按照batch ( 32 ∗ 28 ∗ 28 32*28*28 32∗28∗28) 送入网络的,所以进入predict函数前要先把 img_arr 前添加一个维度。
x_predict = img_arr[tf.newaxis, ...]
第五讲 卷积神经网络
前几讲,使用 “六步法” 搭建了全连接网络,实现了图像识别应用。实践证明,全连接网络对于识别和预测任务都有很好的效果。
卷积神经网络与全连接神经网络的唯一区别就在于神经网络中相邻两层的连接方式。
全连接网络参数个数: ∑ 层 数 [ ( 前 层 ∗ 后 层 ) w + ( 后 层 ) b ] \sum_{层数}[(前层*后层)_w+(后层)_b] ∑层数[(前层∗后层)w+(后层)b]
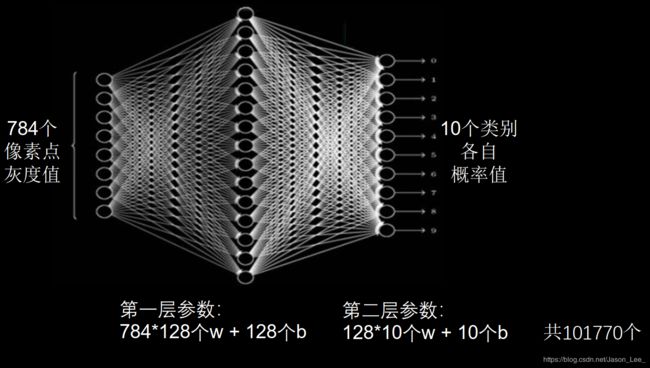
针对MNIST数据集的分辨率仅为 28 ∗ 28 28*28 28∗28 的黑白图像 两层神经网络就包含了 101, 770 个参数。在实际应用中,图像的分辨率远高于此,且大多数是彩色图像,如下图所示。

虽然全连接网络一般被认为是分类预测的最佳网络,但待优化的参数过多,容易导致模型过拟合。 为了解决参数量过大而导致模型过拟合的问题,一般不会将原始图像直接输入,而是先对图像进行特征提取,再将提取到的特征输入全连接网络。如下图所示,就是将汽车图片经过多次特征提取后再输入全连接网络。
5.1 卷积计算过程
卷积计算可认为是一种有效提取图像特征的方法。
-
一般会用一个正方形的卷积核,按指定步长,在输入特征图上滑动,遍历输入特征图中的每个像素点。每一个步长,卷积核会与输入特征图出现重合区域,重合区域对应元素相乘、求和再加上偏置项得到输出特征的一个像素点。
-
- 对于单通道图像(灰度图),使用 3 ∗ 3 ∗ 1 3*3*1 3∗3∗1、 5 ∗ 5 ∗ 1 5*5*1 5∗5∗1 的卷积核;
-
- 对于RGB三通道图像,使用 3 ∗ 3 ∗ 3 3*3*3 3∗3∗3、 5 ∗ 5 ∗ 3 5*5*3 5∗5∗3 的卷积核;
-
- 对于隐含层中深度为n的特征图,使用 3 ∗ 3 ∗ n 3*3*n 3∗3∗n、 5 ∗ 5 ∗ n 5*5*n 5∗5∗n 的卷积核。
-
卷积核的深度必须与输入层的通道数一致,所以输入特征图的深度(channel数)决定了当前层卷积核的深度 n n n ;
每个卷积核在卷积计算后,会得到一层输出特征图,所以当前层卷积核的个数决定了当前层输出特征图的深度。
所以一般只需要指定卷积核的尺寸 3 ∗ 3 3*3 3∗3 或 5 ∗ 5 5*5 5∗5 和卷积核的个数 (即输出层特征图的深度)。 -
所以如果觉得某层模型的特征提取能力不足,可以适当增加该层的卷积核个数,以提高特征提取能力。
卷积核中的参数数量计算如下图所示:
这些参数的更新过程与全连接神经网络一致,同样使用梯度下降法进行参数更新。

单通道卷积核 3 ∗ 3 ∗ 1 3*3*1 3∗3∗1 的计算过程:
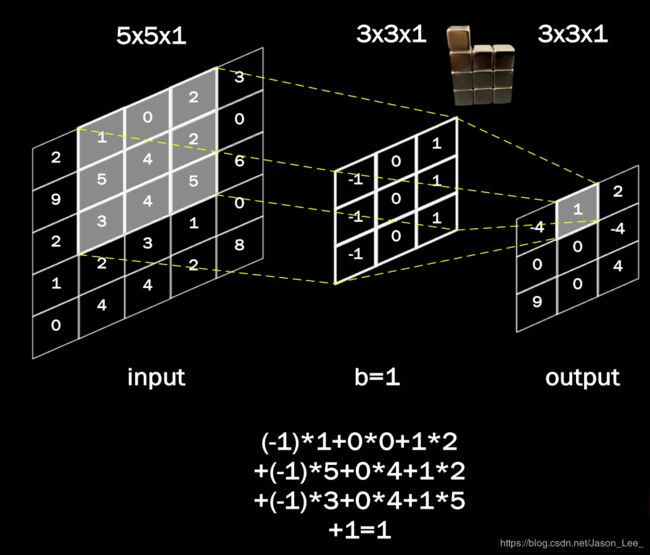
多通道卷积核 3 ∗ 3 ∗ 3 3*3*3 3∗3∗3 或 3 ∗ 3 ∗ n 3*3*n 3∗3∗n 的计算过程:
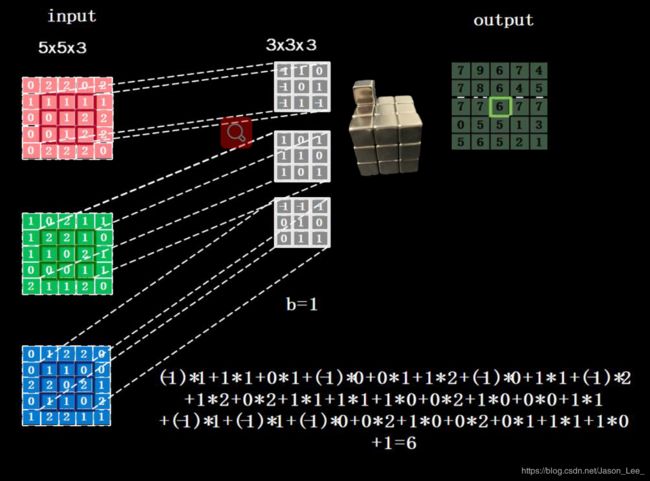
卷积核移动计算过程: 当卷积核遍历完成输入特征图后,就得到了一张输出特征图,完成了一个卷积核的卷积计算过程。当有n个卷积核时,就会有n张输入特征图依次叠加。
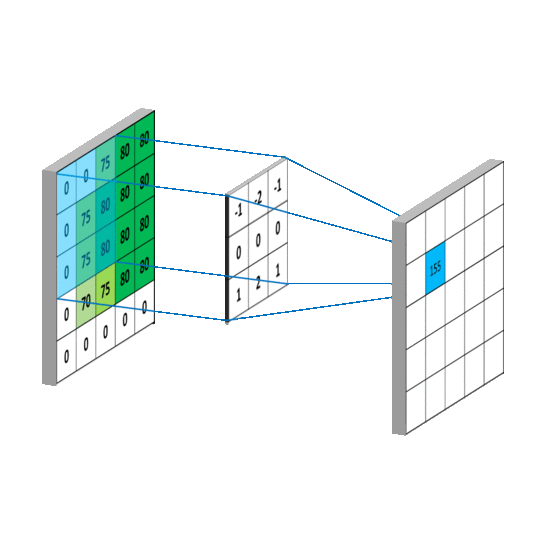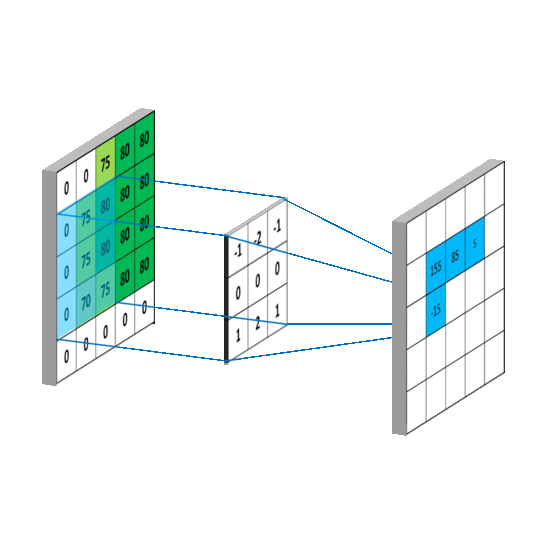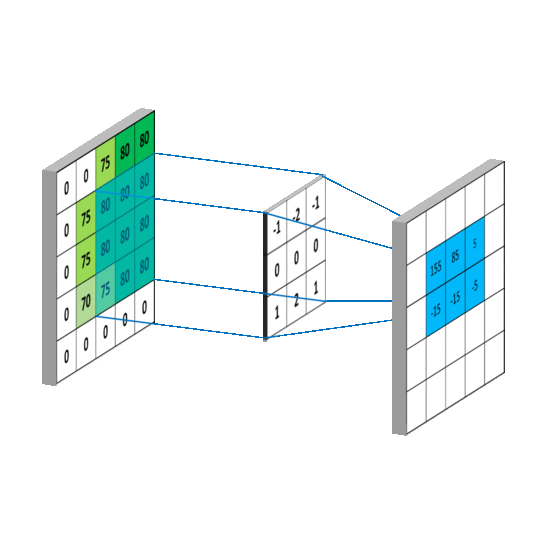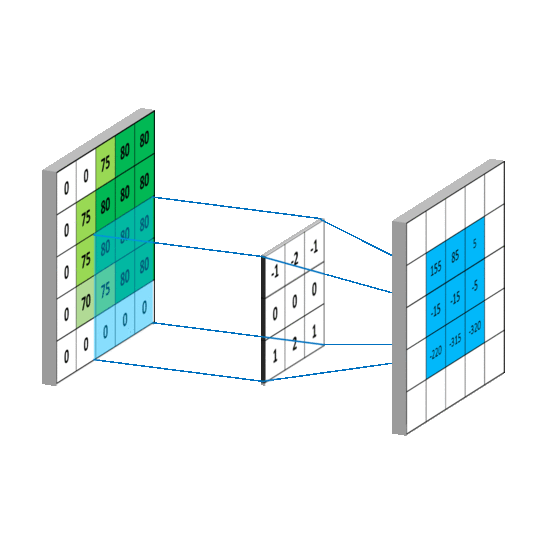
5.2 感受野
感受野(Receptive Field): 卷积神经网络各输出特征图中的每个像素点,在原始输入图片上映射区域的大小。
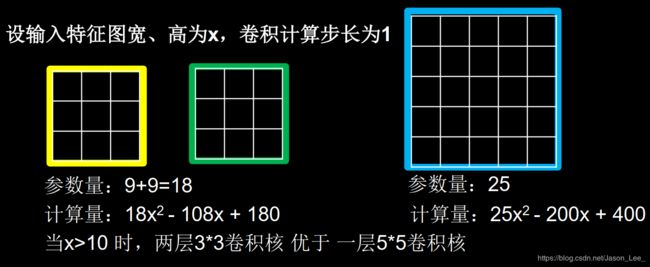
如下图所示,对于一幅 5 ∗ 5 5*5 5∗5 的原始输入图像,经过两层 3 ∗ 3 3*3 3∗3 卷积核作用,和经过一层 5 ∗ 5 5*5 5∗5 的卷积核作用,都得到一个感受野是 5 5 5 的输出特征图。所以这两层 3 ∗ 3 3*3 3∗3 卷积核和一层 5 ∗ 5 5*5 5∗5 的卷积核的特征提取能力是一样的。
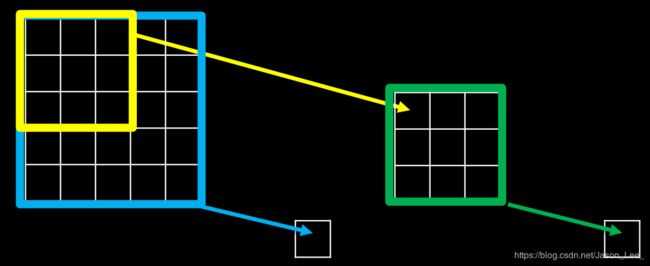
那么,是选择两层 3 ∗ 3 3*3 3∗3 卷积核好?还是选择一层 5 ∗ 5 5*5 5∗5 的卷积核好呢?这时就要考虑他们所承载的参数量和计算量了。
- 例: 对于使用两个 3 ∗ 3 3*3 3∗3 卷积核,在第一层网络中,卷积核需要移动 ( x − 2 ) 2 (x-2)^2 (x−2)2 次,在第二层网络中,卷积核需要移动 ( x − 4 ) 2 (x-4)^2 (x−4)2 次,即两个 3 ∗ 3 3*3 3∗3 卷积核总共需要进行 ( x − 2 ) 2 + ( x − 4 ) 2 = 2 x 2 − 12 x + 20 (x-2)^2+(x-4)^2=2x^2-12x+20 (x−2)2+(x−4)2=2x2−12x+20 次卷积运算。每次卷积运算需要进行 3 ∗ 3 = 9 3*3=9 3∗3=9 次乘加运算。所以使用两个 3 ∗ 3 3*3 3∗3 卷积核共需要进行 18 x 2 − 108 x + 180 18x^2-108x+180 18x2−108x+180 次乘加运算。
5.3 全零填充
在上一节中介绍时,使用尺寸为 n ∗ n n*n n∗n 的卷积核,输出特征图的尺寸相比输入特征图的尺寸,减小了 n − 1 n-1 n−1 。但是有时候,我们希望卷积计算能够使得输入输出特征图的尺寸保持不变。这就需要用到全零填充。
全零填充(padding): 为了保持输出图像尺寸与输入图像一致, 经常会在输入图像周围进行全零填充,如下图所示,在 5 × 5 5×5 5×5 的输入图像周围填 0,则输出特征尺寸同为 5 × 5 5×5 5×5。
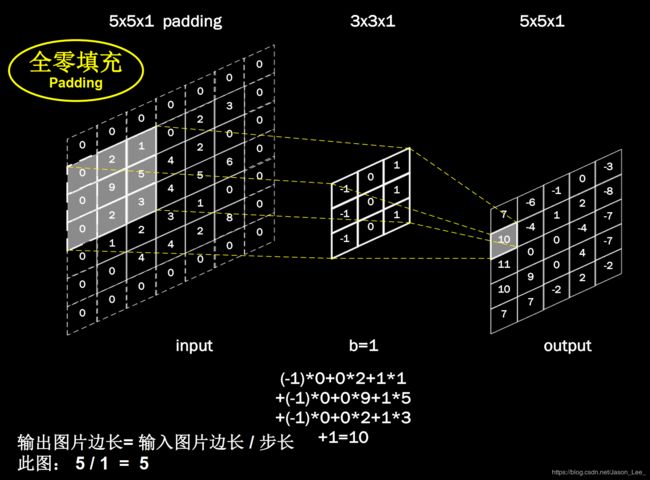
卷积输出特征图维度计算: p a d d i n g = { S A M E ( 使 用 全 0 填 充 ) 输 入 特 征 图 边 长 步 长 ( 向 上 取 整 ) V A L I D ( 不 使 用 全 0 填 充 ) 输 入 特 征 图 边 长 − ( 卷 积 核 边 长 − 1 ) 步 长 ( 向 上 取 整 ) padding=\begin{cases} SAME (使用全0填充) & \frac{输入特征图边长}{步长} & (向上取整) \\ \\ VALID (不使用全0填充) & \frac{输入特征图边长-(卷积核边长-1)}{步长} & (向上取整) \end{cases} padding=⎩⎪⎨⎪⎧SAME(使用全0填充)VALID(不使用全0填充)步长输入特征图边长步长输入特征图边长−(卷积核边长−1)(向上取整)(向上取整)
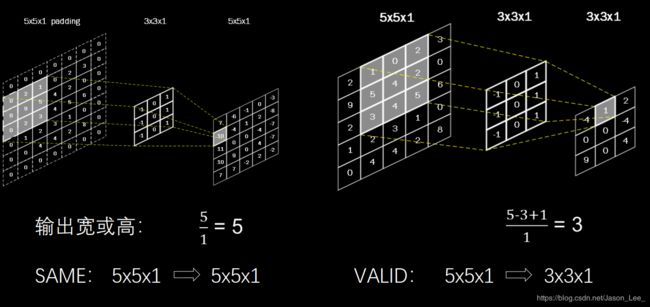
TensorFlow描述全零填充: 用参数padding = ‘SAME’ 或 padding = ‘VALID’表示。
5.4 TensorFlow实现卷积计算层
Tensorflow给出了计算卷积的函数:
tf.keras.layers.Conv2D (filters = 卷积核个数, # 即卷积层输出特征图深度
kernel_size = 卷积核尺寸, # 正方形写核长整数,或(核高h,核宽w)
strides = 滑动步长, # 横纵向相同写步长整数,或(纵向步长h,横向步长w),默认1
padding = “same” or “valid”, # 使用全零填充是“same”, 不使用是“valid”(默认“valid”)
activation = “ relu ” or “ sigmoid ” or “ tanh ” or “ softmax”等, # 如果在该层之后使用了BN,则此处不使用激活函数
input_shape = (高, 宽 , 通道数) #输入特征图维度,可省略
)
举个栗子:
model = tf.keras.models.Sequential([
Conv2D(6, 5, padding='valid', activation='sigmoid'),
MaxPool2D(2, 2),
Conv2D(6, (5, 5), padding='valid', activation='sigmoid'),
MaxPool2D(2, (2, 2)),
Conv2D(filters=6, kernel_size=(5, 5),padding='valid', activation='sigmoid'),
MaxPool2D(pool_size=(2, 2), strides=2),
Flatten(),
Dense(10, activation='softmax')
])
5.5 批标准化 (Batch Normalization, BN)
神经网络对0附近的数据更敏感。但是随着网络层数的增加,特征数据会出现偏离0均值的情况。
- 标准化 (Normalization):可以使数据符合以0为均值,1为标准差的标准正态分布。将偏移的特征数据重新拉回到0附近。
- 批标准化 (Batch Normalization, BN):对一小批数据(batch),做标准化处理 。常用在卷积操作和激活操作之间。
批标准化后,第 k k k 个卷积核的输出特征图(feature map)中第 i i i 个像素点的值: H i ′ k = H i k − μ b a t c h k σ b a t c h k H_i'^k=\frac{H_i^k-\mu_{batch}^k}{\sigma_{batch}^k} Hi′k=σbatchkHik−μbatchk其中, H i k H_i^k Hik表示批标准化前,第 k 个卷积核,输出特征图中第 i i i 个像素点的值; μ b a t c h k = 1 m ∑ i = 1 m H i k \mu_{batch}^k=\frac{1}{m}\sum_{i=1}^mH_i^k μbatchk=m1∑i=1mHik表示批标准化前,第k个卷积核, batch张输出特征图中所有像素点平均值; σ b a t c h k = δ + 1 m ∑ i = 1 m ( H i k − μ b a t c h k ) \sigma_{batch}^k=\sqrt{\delta+\frac{1}{m}\sum_{i=1}^m(H_i^k-\mu_{batch}^k)} σbatchk=δ+m1∑i=1m(Hik−μbatchk)表示批标准化前,第k个卷积核, batch张输出特征图中所有像素点标准差。

一共包含 n n n 个卷积核, b a t c h = 32 batch=32 batch=32,每个卷积核对一个 b a t c h = 32 batch=32 batch=32 的输入特征图进行一次卷积计算输出 32 32 32 张特征图。 μ b a t c h k \mu_{batch}^k μbatchk 即对这 32 张特征图的所有像素值求平均; σ b a t c h k \sigma_{batch}^k σbatchk 即对这 32 张特征图的所有像素值求标准差。
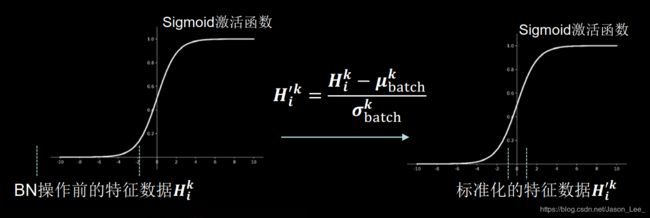
如上图所示,BN操作将原本偏移的数据重新拉回标准正态分布,然后再进入激活函数,使进入激活函数的数据分布在激活函数线性区。 使得输入数据的微小变化,更明显的提现到激活函数的输出,提升了激活函数对输入数据的区分力。
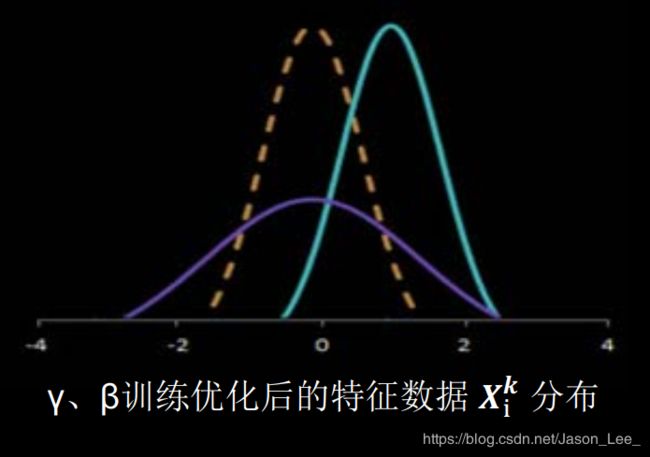
但是,这种标准化方法使得特征数据完全满足标准正态分布,集中在激活函数中心的线性区域,使激活函数丧失了非线性特性,因此在BN操作中为每个卷积核引入可训练参数:缩放因子 γ \gamma γ 和偏移因子 β \beta β,调整批归一化的力度。 X i k = γ k H i ′ k + β k X_i^k=\gamma_kH_i'^k+\beta_k Xik=γkHi′k+βk 在反向传播时,缩放因子 γ \gamma γ 和偏移因子 β \beta β,会与其他可训练参数一同被优化。 使标准正态分布后的特征数据通过缩放因子和偏移因子优化了特征数据分布的宽窄和偏移量,保证了网络的非线性表达力。

TensorFlow API: tf.keras.layers.BatchNormalization()
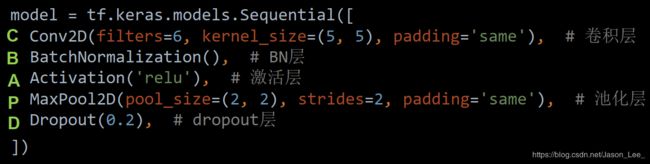
model = tf.keras.models.Sequential([
Conv2D(filters=6, kernel_size=(5, 5), padding='same'), # 卷积层
BatchNormalization(), # BN层
Activation('relu'), # 激活层
MaxPool2D(pool_size=(2, 2), strides=2, padding='same'), # 池化层
Dropout(0.2), # dropout层
])
- 注意:在调用此函数时,需要注意的一个参数是 training,此参数只在调用时指定,在模型进行前向推理时产生作用。
-
- 当
training = True时,BN 操作采用当前 batch 的均值和标准差;
- 当
-
- 当
training = False时,BN 操作采用滑动平均(running)的均值和标准差。
- 当
- 在 Tensorflow 中,通常会指定 training = False,可以更好地反映模型在测试集上的真实效果。
- 滑动平均(running):滑动平均,即通过一个个历史 batch 的叠加,最终趋向数据集整体分布的过程,在测试集上进行推理时,滑动平均的参数也就是最终保存的参数。
- 此外,Tensorflow 中的 BN 函数其实还有很多参数,其中比较常用的是 momentum,即动量参数,与 sgd 优化器中的动量参数含义类似但略有区别,具体作用为滑动平均 r u n n i n = m o m e n t u m ∗ r u n n i n g + ( 1 – m o m e n t u m ) ∗ b a t c h runnin=momentum * running + (1 – momentum) * batch runnin=momentum∗running+(1–momentum)∗batch,一般设置一个比较大的值,在 Tensorflow 框架中默认为 0.99。
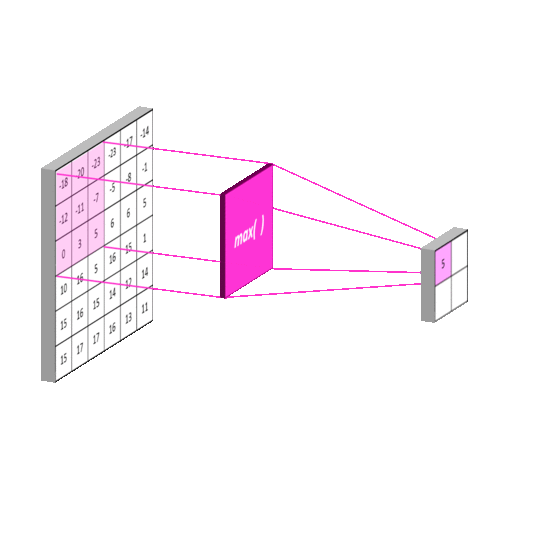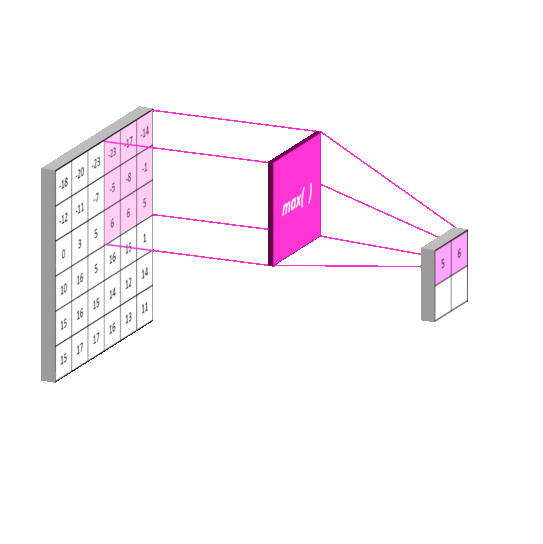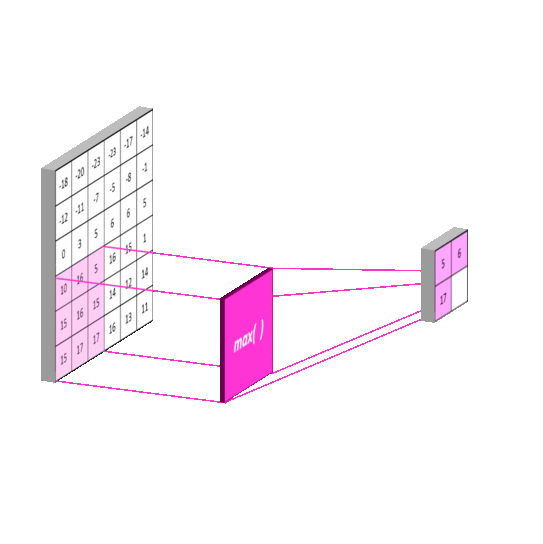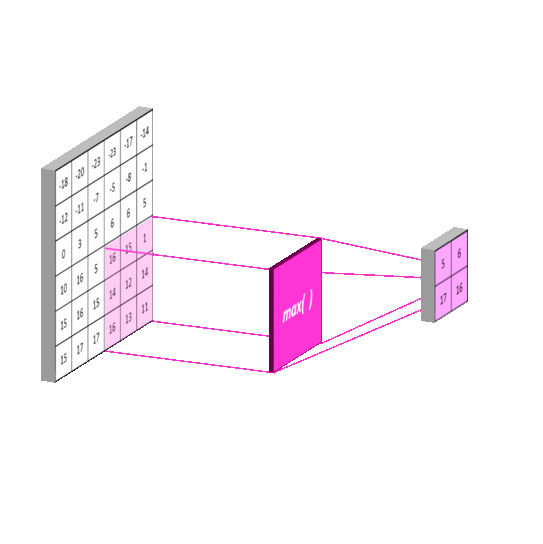
5.6 池化
池化(pooling): 池化操作用于减少卷积神经网络中的特征参数量。
池化的主要方法有 最大池化 和 均值池化 。最大池化可以提取图片纹理,均值池化可以保留背景特征,如果使用 2 ∗ 2 2*2 2∗2 的池化核对输入图片以步长 2 进行池化,输出图片将变为输入图片的 1/4 大小。
tf.keras.layers.MaxPool2D(pool_size=池化核尺寸, # 正方形写核长整数,或(核高h,核宽w)
strides=池化步长, # 步长整数, 或(纵向步长h,横向步长w),默认为pool_size
padding=‘valid’or‘same’) # 使用全零填充是“same”, 不使用是“valid”(默认)
tf.keras.layers.AveragePooling2D(pool_size=池化核尺寸, # 正方形写核长整数,或(核高h,核宽w)
strides=池化步长, # 步长整数, 或(纵向步长h,横向步长w),默认为pool_size
padding=‘valid’or‘same’) # 使用全零填充是“same”, 不使用是“valid”(默认)
举个栗子:
model = tf.keras.models.Sequential([
Conv2D(filters=6, kernel_size=(5, 5), padding='same'), # 卷积层
BatchNormalization(), # BN层
Activation('relu'), # 激活层
MaxPool2D(pool_size=(2, 2), strides=2, padding='same'), # 池化层
Dropout(0.2), # dropout层
])
5.7 舍弃 Dropout
舍弃(Dropout): 在神经网络的训练过程中, 将隐含层的部分神经元按照一定概率从神经网络中暂时舍弃,使用时被舍弃的神经元恢复链接。
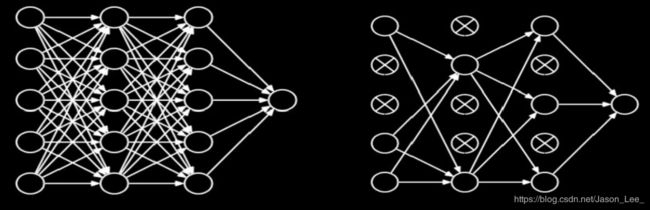
TensorFlow API: tf.keras.layers.Dropout(舍弃的概率)
举个栗子:
model = tf.keras.models.Sequential([
Conv2D(filters=6, kernel_size=(5, 5), padding='same'), # 卷积层
BatchNormalization(), # BN层
Activation('relu'), # 激活层
MaxPool2D(pool_size=(2, 2), strides=2, padding='same'), # 池化层
Dropout(0.2), # dropout层随机舍弃20%的神经元
])
5.8 卷积神经网络
卷积神经网络:通过卷积层借助卷积核提取特征后,送入全连接网络,进行识别预测任务。
卷积神经网络主要模块:
卷积层→BN层→激活层→池化层→Dropout层→FC层
卷积是什么?
卷积层的实际作用就是一个特征提取器,就是CBAPD。
卷积特征提取借助卷积核实现参数空间共享,借助卷积计算层提取空间特征后,送入全连接网络。
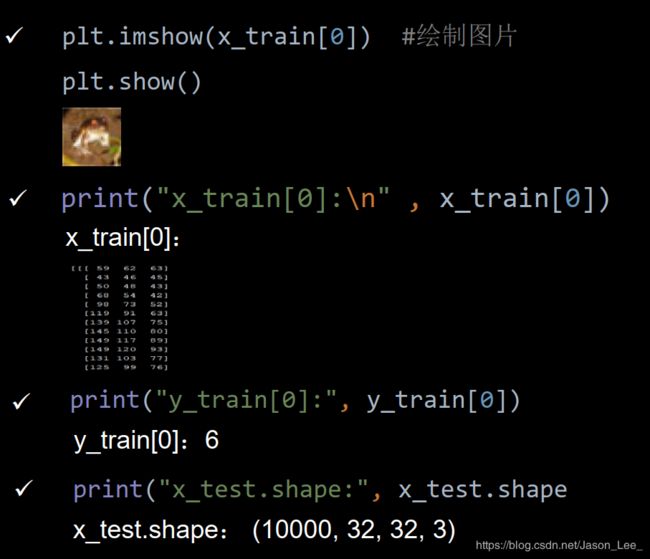
5.9 CIFAR10数据集
提供 5 万张 32 ∗ 32 32*32 32∗32 像素点的十分类彩色图片和标签,用于训练。
提供 1 万张 32 ∗ 32 32*32 32∗32 像素点的十分类彩色图片和标签,用于测试。
cifar10 = tf.keras.datasets.cifar10
(x_train, y_train), (x_test, y_test) = cifar10.load_data()
观察CIFAR10数据集:
5.10 卷积神经网络搭建示例
搭建一个一层卷积、两层全连接的网络。
5.11 LeNet、AlexNet、VGGNet、InceptionNet、ResNet
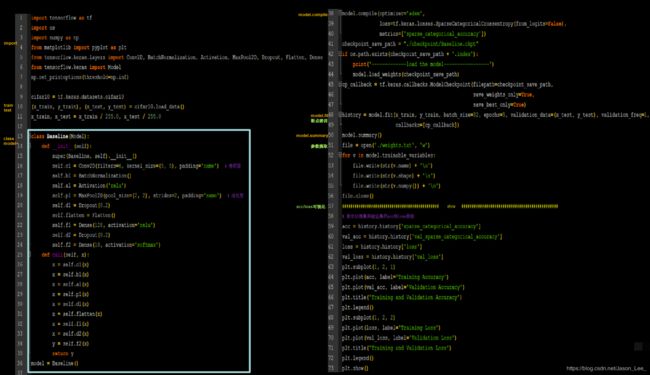
接下来,将使用“六步法”实现LeNet、AlexNet、VGGNet、InceptionNet、ResNet卷积神经网络。
LeNet
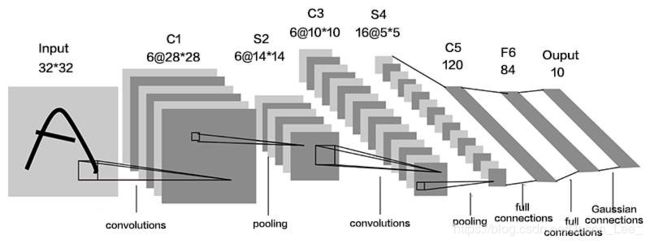
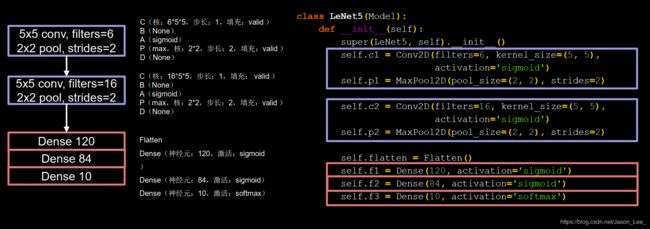
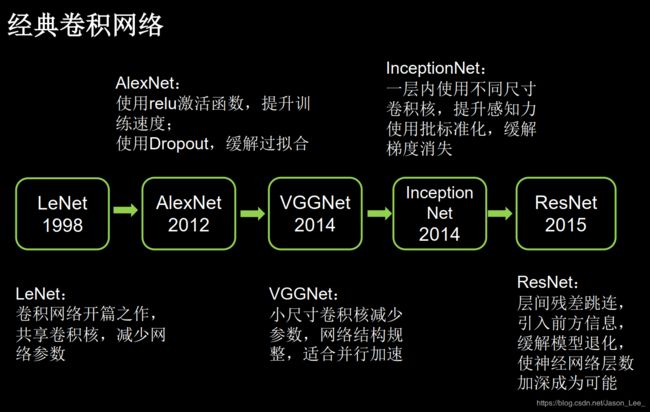
LeNet 1 由Yann LeCun于1998年提出,卷积网络开篇之作。卷积网络通过共享卷积核,减少了网络的参数。
在统计神经网络层数时,一般只统计卷积计算层和全连接计算层,其余操作可以认为是卷积计算层的附属操作。
LeNet一共有五层网络,包含两层卷积层和三层全连接层。LeNet提出时,还没有BN操作和Dropout操作,该时代的主流激活函数为sigmoid激活函数。
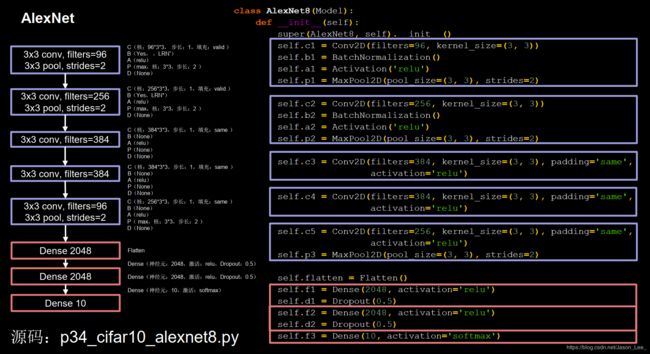
AlexNet
AlexNet 2 络诞生于2012年,是Hinton的代表作之一,当年ImageNet竞赛的冠军, Top5错误率为16.4%。AlexNet 使用了Relu激活函数,提升了训练速度,使用Dropout缓解了过拟合
AlexNet共有8层,包含5层卷积层和3层全连接层。
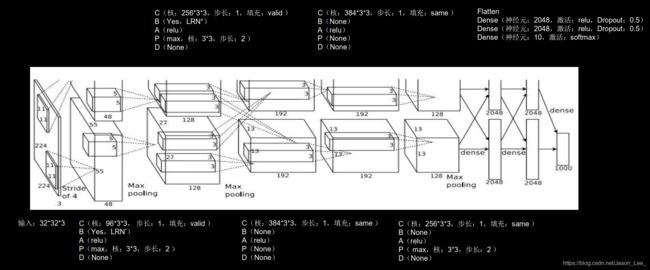
注:原文使用LRN(local response normalization) 局部响应标准化,本课程使用BN(Batch Normalization)替代。 近年来,LRN用的很少,其功能与BN相似。
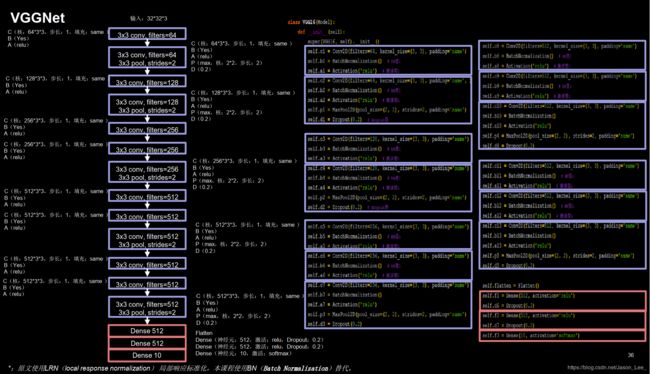
VGGNet
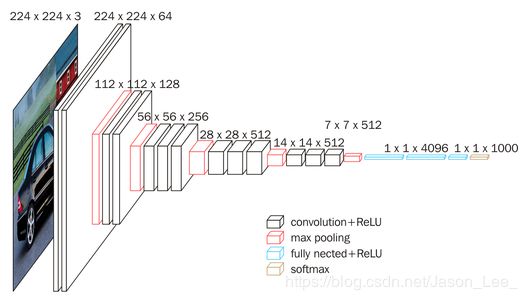
VGGNet 3 诞生于2014年,当年ImageNet竞赛的亚军, Top5错误率减小到7.3%。
VGGNet使用小尺寸卷积核,在减少参数的同时,提高了识别准确率。VGGNet的网络结构规整,非常适合硬件加速。
以16层VGGNet网络为例: 包含13层卷积层和3层FC层。各层卷积核个数从64逐渐增加至512,越靠后,特征图尺寸越小,通过增加卷积核的个数,增加了特征图深度,保持了信息的承载能力。
InceptionNet
InceptionNet 4 诞生于2014年,当年ImageNet竞赛冠军, Top5错误率为6.67%。
InceptionNet引入了Inception结构块,在同一层网络内使用不同尺寸的卷积核,提升了模型感知力,使用了BN,缓解了梯度消失。
Inception结构块
InceptionNet的核心是他的基本单元Inception结构块。 无论是 GooGLeNet——Inception v1 ,还是InceptionNet的后续版本(v2,v3,v4)都是基于Inception结构块搭建的网络。
Inception结构块在同一层网络中使用了多个尺寸的卷积核,可以提取不同尺度的特征。
- 通过 1 ∗ 1 1*1 1∗1 卷积核作用到输入特征图的每个像素点,通过设定少于输入特征图深度的 1 ∗ 1 1*1 1∗1 卷积核个数,减少了输出特征图深度,起到了降维的作用。 减少了参数量和计算量。
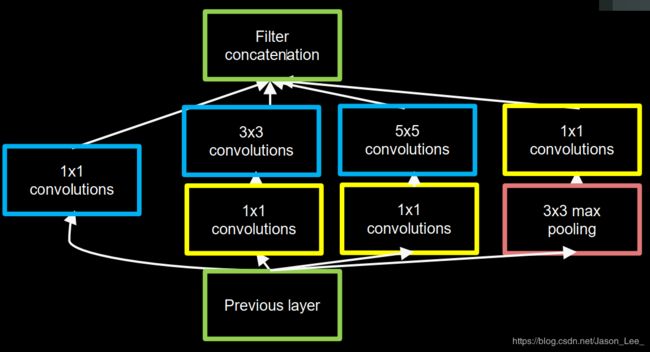
下图为一个Inception结构块的示意图:
- 经过 1 ∗ 1 1*1 1∗1 卷积核输出到卷积连接器;
- 经过 1 ∗ 1 1*1 1∗1 卷积核配合 3 ∗ 3 3*3 3∗3 卷积核输出到卷积连接器;
- 经过 1 ∗ 1 1*1 1∗1 卷积核配合 5 ∗ 5 5*5 5∗5 卷积核输出到卷积连接器;
- 经过 3 ∗ 3 3*3 3∗3 最大池化核配合 1 ∗ 1 1*1 1∗1 卷积核输出到卷积连接器。
送到卷积连接器的特征数据尺寸相同。 卷积连接器会将收到的这四路特征数据按深度方向拼接,生成Inception结构块的输出。
编写代码实现Inception结构块:
因为Inception结构块中的所有卷积均为CBA无PD结构,使用编写 class ConvBNRelu(Model): 来减小代码长度。
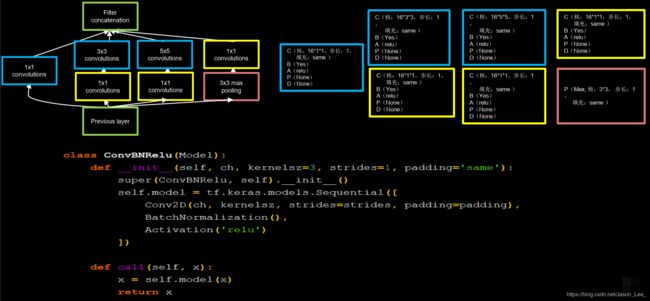
在 class ConvBNRelu(Model): 基础上使用 class 实现Inception结构块:
下图中,x = tf.concat([x1, x2_2, x3_3, x4_2], axis=3) 指按照 axis=3 深度方向拼接四路输出特征。
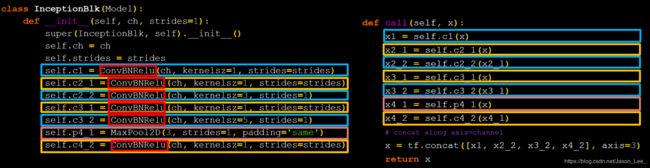
搭建一个精简的 InceptionNet
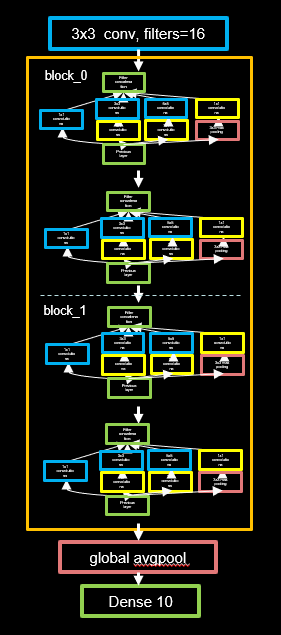
有了Inception结构块后,就可以搭建一个精简的InceptionNet了。网络共包含10层,分别为:
- 第一层采用16个 3 ∗ 3 3*3 3∗3卷积核,步长为1,全零填充,采用BN操作,Relu激活;
- 随后是4个Inception结构块顺序相连,每两个Inception结构块组成一个block;
-
- 第一个Inception结构块卷积步长为2,第二个Inception结构块卷积步长为1;
这一操作使得第一个Inception结构块输出特征图尺寸减半,因此需要把输出特征图深度加深为2倍self.out_channels *= 2。
- 第一个Inception结构块卷积步长为2,第二个Inception结构块卷积步长为1;
-
- block_0设置的输出通道数为16,经过了4个分支,输出的深度为 4 ∗ 16 = 64 4*16=64 4∗16=64。
-
- 因为使用
self.out_channels *= 2将通道数加倍,所以block_1通道数为block_0的两倍,即block_1的通道数为32,经过了4个分支,输出的深度为 4 ∗ 32 = 128 4*32=128 4∗32=128.
- 因为使用
- 128个通道的输出数据会被送入平均池化,再送人10分类全连接网络。
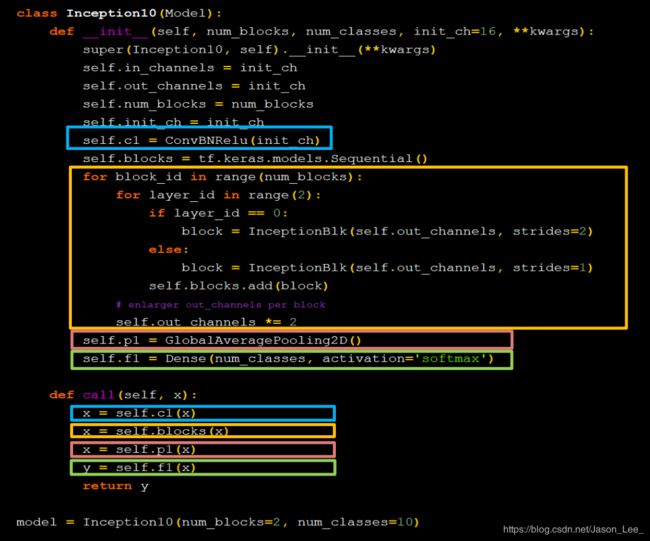
编写代码实现:
定义类Inception10时,设定了默认 init_ch=16 ,即默认输出深度为16,定义 class ConvBNRelu(Model): 时,定义了默认卷积核边长为3,步长为1,全零填充。
ResNet
ResNet 5 诞生于2015年,当年ImageNet竞赛冠军, Top5错误率为3.57%。
ResNet 提出了层间残差跳连,引入了前方信息,缓解了梯度消失,使得更深的神经网络的实现成为可能。前几小节介绍的LeNet、AlexNet、VGGNet和InceptionNet的层数:
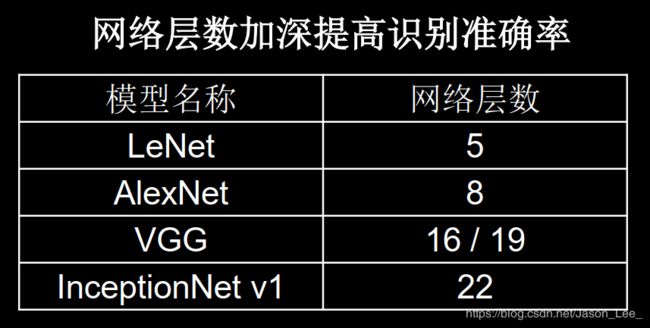
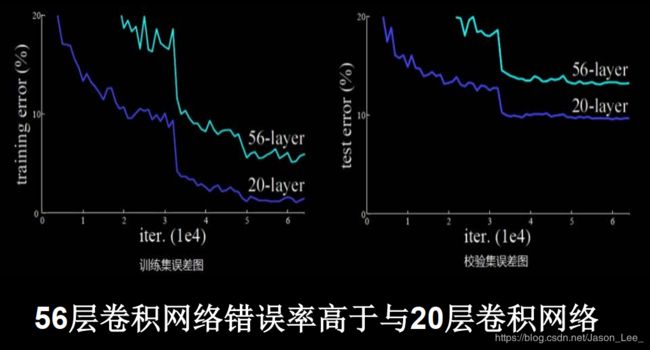
可见,在探索卷积实现特征提取的道路上,通过加深网络层数,取得了越来越好的效果。而ResNet的作者何凯明在CIFAR10数据集上的实验发现56层卷积网络错误率高于与20层卷积网络。
跳跃连接 与 ResNet 结构块
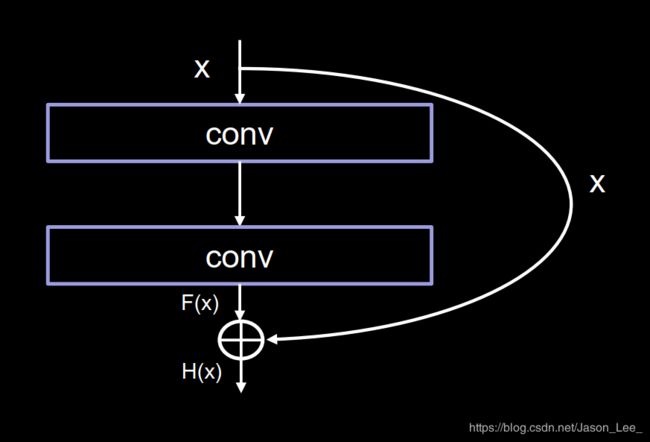
作者认为,单纯堆叠网络层数,会使神经网络模型发生 退化现象 ,以至于后面的特征丢失了前面特征的原本模样。所以,作者引入了 跳跃连接 将前面的特征直接接到了后面。使得输出结果 H ( x ) H(x) H(x)包含了堆叠卷积的非线性输出 F ( x ) F(x) F(x) 和跳过这两层堆叠卷积层,直接连接的恒等映射 x x x ,即 H ( x ) = F ( x ) + x H(x)=F(x)+x H(x)=F(x)+x。这一操作有效缓解了深层神经网络层数过多所导致的 退化现象 。使得神经网络可以向着更深层发展。
注: ResNet中的特征图相加与InceptionNet中的特征图相加方式不同:
- ResNet块中的“+”是特征图对应元素值相加(矩阵值相加),所以 F ( x ) F(x) F(x) 与 x x x 特征图的维度应该完全相同。
- Inception块中的“+”是沿深度方向叠加(千层蛋糕层数叠加)。
跳跃连接的两种方式
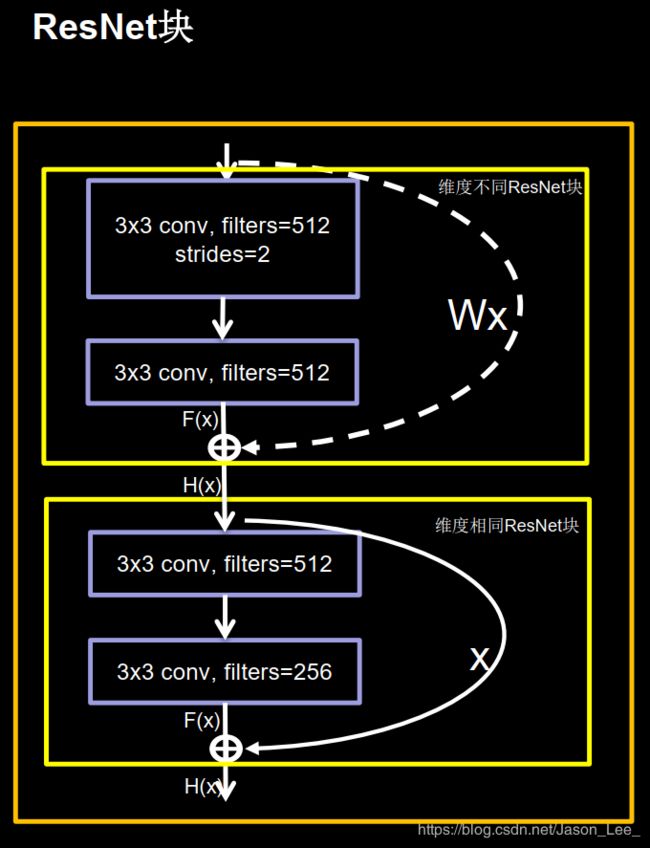
ResNet 结构块中的跳跃连接有两种情况:
- 一种情况是下图中的实线连接,这种情况是指两层堆叠卷积没有改变特征图的维度,可以直接将特征图 F ( x ) F(x) F(x) 与特征图 x x x 相加;
- 另一种情况是下图中的虚线连接,这种情况下,两层堆叠卷积改变了特征图的维度,需要借助 1 ∗ 1 1*1 1∗1 卷积来调整 x x x 的维度(主要指特征图深度),使 特征图 F ( x ) F(x) F(x) 与特征图 x x x 维度一致。
搭建 ResNet-18
下图为ResNet-18的网络结构:
第一层为一个卷积,然后为8个ResNet结构块共16层卷积层,每两个ResNet结构块构成一个ResNet block,接着通过全局平均池化层,最后进入十分类全连接层。
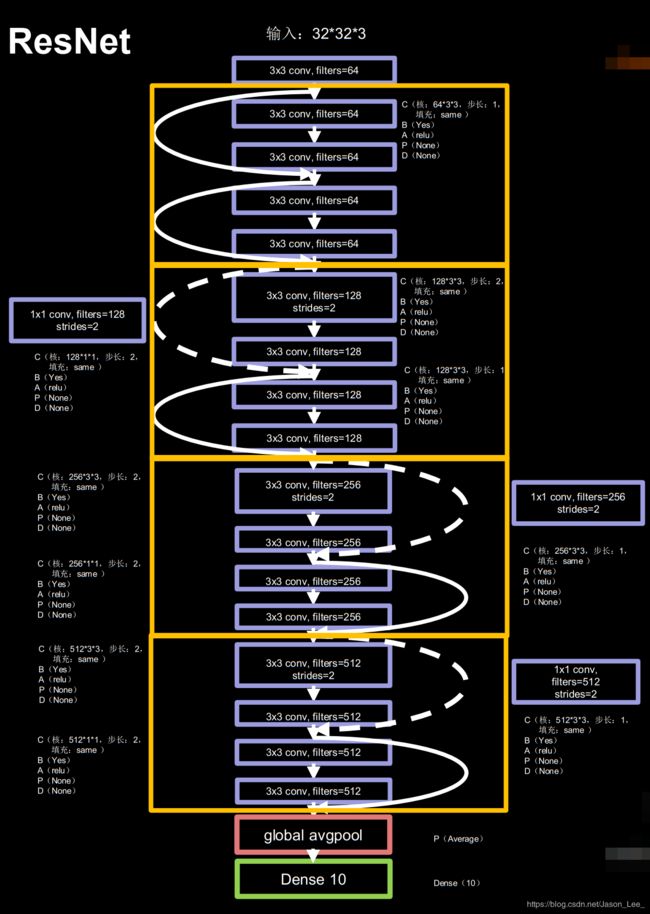
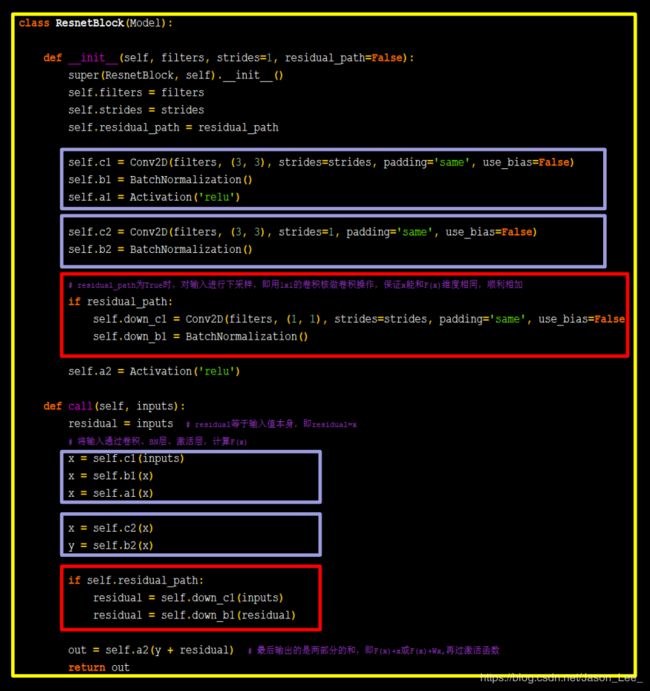
根据ResNet结构块和ResNet-18网络结构编写出相应代码:
class ResNet18(Model):
def __init__(self, block_list, initial_filters=64): # block_list表示每个block有几个卷积层
super(ResNet18, self).__init__()
self.num_blocks = len(block_list) # 共有几个block
self.block_list = block_list
self.out_filters = initial_filters
self.c1 = Conv2D(self.out_filters, (3, 3), strides=1, padding='same', use_bias=False)
self.b1 = BatchNormalization()
self.a1 = Activation('relu')
self.blocks = tf.keras.models.Sequential()
# 构建ResNet网络结构
for block_id in range(len(block_list)): # 第几个resnet block
for layer_id in range(block_list[block_id]): # 第几个卷积层
if block_id != 0 and layer_id == 0: # 对除第一个block以外的每个block的输入进行下采样
block = ResnetBlock(self.out_filters, strides=2, residual_path=True)
else:
block = ResnetBlock(self.out_filters, residual_path=False)
self.blocks.add(block) # 将构建好的block加入resnet
self.out_filters *= 2 # 下一个block的卷积核数是上一个block的2倍
self.p1 = tf.keras.layers.GlobalAveragePooling2D()
self.f1 = tf.keras.layers.Dense(10, activation='softmax', kernel_regularizer=tf.keras.regularizers.l2())
def call(self, inputs):
x = self.c1(inputs)
x = self.b1(x)
x = self.a1(x)
x = self.blocks(x)
x = self.p1(x)
y = self.f1(x)
return y
5.12 经典卷积神经网络小结
当网络框架搭建好后,还需要尝试更改学习率等超参数,微调网络结构,通过一些优化策略,提升CIFAR10测试集的准确率。当模型在CIFAR10测试集的准确率达到90%以上时,则模型效果较好。
第六讲 循环神经网络 (Recurrent Neural Network, RNN)
本讲目标: 使用RNN实现连续数据的预测。
循环神经网络: 借助循环核提取时间特征后,送入全连接网络。
6.1 循环核
对于与时间、序列相关的数据,是可以根据上文预测出下文的。比如“鱼离不开__”。自然就会想到填“水”。这种预测就是通过 脑记忆体 提取历史数据的特征,预测出接下来最可能发生的情况。
人脑中的 脑记忆体 在人工神经网络中就对应了 循环核: 参数时间共享,循环层提取时间信息。循环核具有记忆力,通过不同时刻的参数共享,实现了对时间序列的信息提取。
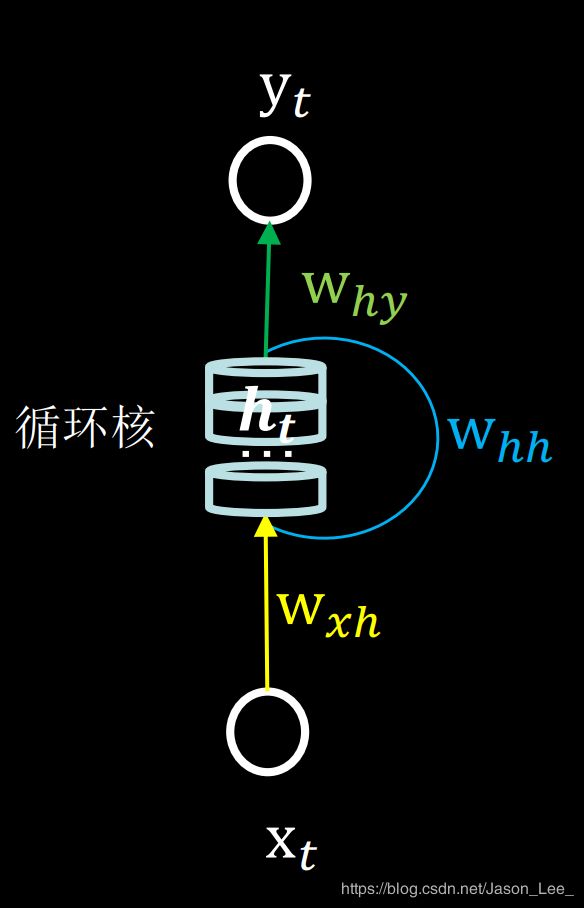
下图展示了一个循环核的基本结构。中间的圆柱部分就是记忆体,记忆体的下面 w x h w_{xh} wxh、侧面 w h h w_{hh} whh、上面 w h y w_{hy} why分别由三组带训练的参数矩阵。可以设定记忆体的个数,改变记忆容量。 当记忆体个数被指定后,输入 x t x_t xt 与输出 y t y_t yt 的维度也自然被指定,周围带训练参数的维度也就被限定了,记忆体内存储着每个时刻的状态信息 h t h_t ht 。该循环体用表达式可以表述为: h t = tanh ( x t ∗ w x h + h t − 1 ∗ w h h + b h ) y t = softmax ( h t ∗ w h y + b y ) \begin{aligned} & h_t=\text{tanh}(x_t*w_{xh}+h_{t-1}*w_{hh}+b_h) \\ & y_t=\text{softmax}(h_t*w_{hy}+b_y) \end{aligned} ht=tanh(xt∗wxh+ht−1∗whh+bh)yt=softmax(ht∗why+by)在前向传播时,记忆体内存储的状态信息 h t h_t ht ,在每个时刻都被刷新。三个参数矩阵 w x h w_{xh} wxh、 w h h w_{hh} whh、 w h y w_{hy} why 始终固定不变。只有在反向传播时,这三个参数矩阵,才会被梯度下降法更新。
这与人类的记忆预测原理是一致的。人脑中的记忆体,每个时刻都根据当前的输入更新,当前的预测推理,是根据以往的知识积累,用固化下来的参数矩阵,进行推理预测。
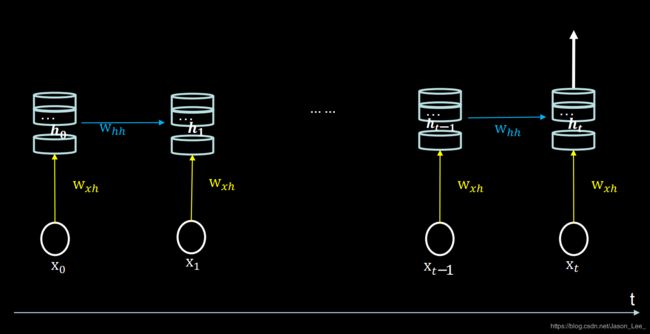
6.2 循环核按照时间步展开
按照时间步展开,就是将循环核按照时间轴方向展开,如下图所示。
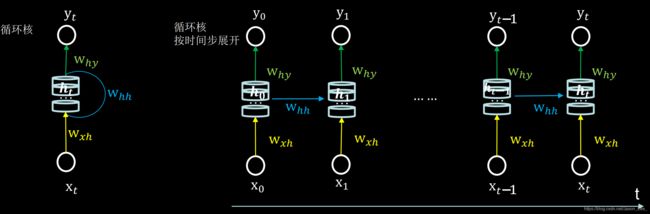
循环神经网络: 借助循环核提取时间特征后,送入全连接网络。 y t y_t yt是整个循环网络的末层,从公式中可以看出,该层就是一个全连接网络。借助全连接网络,实现连续数据预测。 h t = tanh ( x t ∗ w x h + h t − 1 ∗ w h h + b h ) y t = softmax ( h t ∗ w h y + b y ) \begin{aligned} & h_t=\text{tanh}(x_t*w_{xh}+h_{t-1}*w_{hh}+b_h) \\ & y_t=\text{softmax}(h_t*w_{hy}+b_y) \end{aligned} ht=tanh(xt∗wxh+ht−1∗whh+bh)yt=softmax(ht∗why+by)
6.3 循环计算层
每个循环核构成一层循环计算层,循环计算层的层数是向输出方向增长的,如下图所示。每个循环核中的记忆体的个数,是根据需求任意指定的。
6.4 TensorFlow描述循环计算层
TensorFlow API:
# activation=‘激活函数’ (不写,默认使用tanh)
# return_sequences=True 各个时间步均输出ht
# return_sequences=False 仅在最后一个时间步输出ht(默认)
# 一般,最后一层循环核使用False,中间层循环核选择True。
tf.keras.layers.SimpleRNN(记忆体个数, activation=‘激活函数’ ,
return_sequences=是否每个时刻输出ht到下一层)
# 举个栗子:
tf.keras.layers.SimpleRNN(3, return_sequences=True)
下图展示了 return_sequences=True 情况:循环核将在每个时刻把 h t h_t ht 传递到下一层。
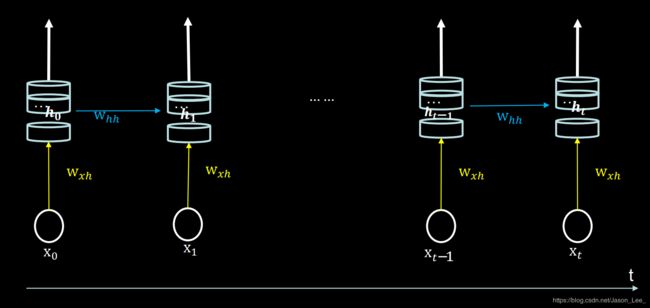
下图展示了 return_sequences=False 情况:循环核仅在最后一个时刻把 h t h_t ht 传递到到下一层。
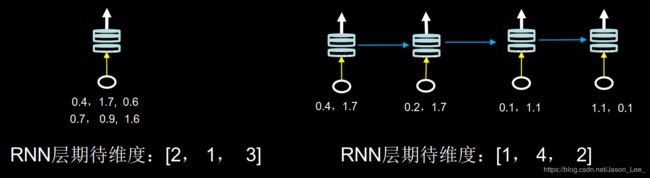
注意:API对送入循环层的数据维度是又要求的。要求,送入循环层的数据是三维的:x_train维度=[送入样本数, 循环核时间展开步数, 每个时间步输入特征个数]
6.5 循环计算过程Ⅰ
字母预测任务: 输入a预测出b,输入b预测出c,输入c预测出d,输入d预测出e,输入e预测出a。
神经网络的输入都是数字,所以需要先对 a, b, c, d, e 五个字母进行编码,最常用的是 one-hot 独热编码。
| one-hot encoding | 字母 |
|---|---|
| 10000 | a |
| 01000 | b |
| 00100 | c |
| 00010 | d |
| 00001 | e |
如下图所示,记忆体初始状态储存值为 h 0 = [ 0 , 0 , 0 ] h_0=[0, 0, 0] h0=[0,0,0] ,计算第一个时刻 h t = tanh ( x t ∗ w x h + h t − 1 ∗ w h h + b h ) = tanh ( [ − 2.3 , 0.8 , 1.1 ] + [ 0 , 0 , 0 ] + [ 0.5 , 0.3 , − 0.2 ] ) = tanh ( [ − 1.8 , 1.1 , 0.9 ] ) = [ − 0.9 , 0.8 , 0.7 ] \begin{aligned}h_t & =\text{tanh}(x_t*w_{xh}+h_{t-1}*w_{hh}+b_h) \\ & = \text{tanh}([-2.3, 0.8, 1.1 ] + [0, 0, 0] + [0.5, 0.3, -0.2]) \\ & = \text{tanh}([-1.8, 1.1, 0.9]) \\ & =[-0.9, 0.8, 0.7]\end{aligned} ht=tanh(xt∗wxh+ht−1∗whh+bh)=tanh([−2.3,0.8,1.1]+[0,0,0]+[0.5,0.3,−0.2])=tanh([−1.8,1.1,0.9])=[−0.9,0.8,0.7]进而计算得预测结果: y t = softmax ( h t ∗ w h y + b y ) = softmax ( [ − 0.7 , − 0.6 , 2.9 , 0.7 , − 0.8 ] + [ 0.0 , 0.1 , 0.4 , − 0.7 , 0.1 ] ) = softmax ( [ − 0.7 − 0.53.30.0 − 0.7 ] ) = [ 0.02 , 0.02 , 0.91 , 0.03 , 0.02 ] \begin{aligned}y_t & =\text{softmax}(h_t*w_{hy}+b_y) \\ & = \text{softmax}([-0.7, -0.6, 2.9, 0.7, -0.8] + [ 0.0, 0.1, 0.4, -0.7, 0.1]) \\ & = \text{softmax}([-0.7 -0.5 3.3 0.0 -0.7]) \\ & = [0.02, 0.02, 0.91, 0.03, 0.02 ] \end{aligned} yt=softmax(ht∗why+by)=softmax([−0.7,−0.6,2.9,0.7,−0.8]+[0.0,0.1,0.4,−0.7,0.1])=softmax([−0.7−0.53.30.0−0.7])=[0.02,0.02,0.91,0.03,0.02]所以预测输出为 [ 0.02 , 0.02 , 0.91 , 0.03 , 0.02 ] [0.02, 0.02, 0.91, 0.03, 0.02 ] [0.02,0.02,0.91,0.03,0.02] ,91%的概率为 C 。
6.6 TensorFlow实现字母预测任务Ⅰ
使用TensorFlow实现上述只包含一个循环计算层的字母预测任务。
import numpy as np
import tensorflow as tf
from tensorflow.keras.layers import Dense, SimpleRNN
import matplotlib.pyplot as plt
import os
# 字母one-hot编码
input_word = "abcde"
w_to_id = {'a': 0, 'b': 1, 'c': 2, 'd': 3, 'e': 4} # 单词映射到数值id的词典
id_to_onehot = {0: [1., 0., 0., 0., 0.], 1: [0., 1., 0., 0., 0.], 2: [0., 0., 1., 0., 0.],
3: [0., 0., 0., 1., 0.], 4: [0., 0., 0., 0., 1.]} # id编码为one-hot
#%% train、test
x_train = [id_to_onehot[w_to_id['a']], id_to_onehot[w_to_id['b']], id_to_onehot[w_to_id['c']],
id_to_onehot[w_to_id['d']], id_to_onehot[w_to_id['e']]]
y_train = [w_to_id['b'], w_to_id['c'], w_to_id['d'], w_to_id['e'], w_to_id['a']]
# 打乱训练集顺序
np.random.seed(7)
np.random.shuffle(x_train)
np.random.seed(7)
np.random.shuffle(y_train)
tf.random.set_seed(7)
# 使x_train符合SimpleRNN输入要求:[送入样本数, 循环核时间展开步数, 每个时间步输入特征个数]。
# 此处整个数据集送入,送入样本数为len(x_train);输入1个字母出结果,循环核时间展开步数为1; 表示为独热码有5个输入特征,每个时间步输入特征个数为5
x_train = np.reshape(x_train, (len(x_train), 1, 5))
y_train = np.array(y_train)
#%% Sequential
model = tf.keras.Sequential([
SimpleRNN(3),
Dense(5, activation='softmax')
])
#%% compile
model.compile(optimizer=tf.keras.optimizers.Adam(0.01),
loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=False),
metrics=['sparse_categorical_accuracy'])
#%% 模型保存
if os.path.exists(checkpoint_save_path + '.index'):
print('-------------load the model-----------------')
model.load_weights(checkpoint_save_path)
cp_callback = tf.keras.callbacks.ModelCheckpoint(filepath=checkpoint_save_path,
save_weights_only=True,
save_best_only=True,
monitor='loss') # 由于fit没有给出测试集,不计算测试集准确率,根据loss,保存最优模型
#%% fit
history = model.fit(x_train, y_train, batch_size=32, epochs=100, callbacks=[cp_callback])
#%% summary
model.summary()
#%% show
# 显示训练集和验证集的acc和loss曲线
acc = history.history['sparse_categorical_accuracy']
loss = history.history['loss']
plt.subplot(1, 2, 1)
plt.plot(acc, label='Training Accuracy')
plt.title('Training Accuracy')
plt.legend()
plt.subplot(1, 2, 2)
plt.plot(loss, label='Training Loss')
plt.title('Training Loss')
plt.legend()
plt.show()
#%% predict
preNum = int(input("input the number of test alphabet:"))
for i in range(preNum):
alphabet1 = input("input test alphabet:")
alphabet = [id_to_onehot[w_to_id[alphabet1]]]
# 使alphabet符合SimpleRNN输入要求:[送入样本数, 循环核时间展开步数, 每个时间步输入特征个数]。此处验证效果送入了1个样本,送入样本数为1;输入1个字母出结果,所以循环核时间展开步数为1; 表示为独热码有5个输入特征,每个时间步输入特征个数为5
alphabet = np.reshape(alphabet, (1, 1, 5))
result = model.predict([alphabet])
pred = tf.argmax(result, axis=1)
pred = int(pred)
tf.print(alphabet1 + '->' + input_word[pred])
6.7 循环计算过程Ⅱ
前面介绍了输入1个字母,预测下一个字母的RNN。
如果将循环核按照时间步展开,连续输入多个字母,一层下一个字母的例子。
连续输入四个字母,预测下一个字母。
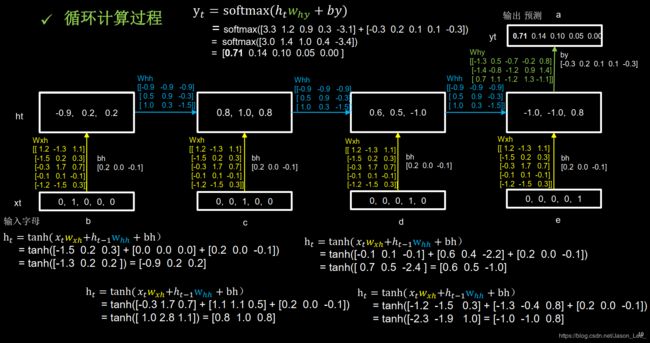
下图展示了按时间步展开的循环核计算过程,推理过程中,三个参数矩阵 w x h w_{xh} wxh、 w h h w_{hh} whh 以及偏置 b h b_h bh 始终保持不变,仅更新记忆体存储的内容。 h t = tanh ( x t ∗ w x h + h t − 1 ∗ w h h + b h ) y t = softmax ( h t ∗ w h y + b y ) \begin{aligned} & h_t=\text{tanh}(x_t*w_{xh}+h_{t-1}*w_{hh}+b_h) \\ & y_t=\text{softmax}(h_t*w_{hy}+b_y) \end{aligned} ht=tanh(xt∗wxh+ht−1∗whh+bh)yt=softmax(ht∗why+by)下图展示的是设置 return_sequences=False 仅在最后一个时间步输出ht(默认) 的情况。
6.8 TensorFlow实现字母预测任务Ⅱ
关于 x_train 维度、记忆体个数
使x_train符合SimpleRNN输入要求:[送入样本数, 循环核时间展开步数, 每个时间步输入特征维数]。
送入样本数=训练集样本数
记忆体个数可自行设置,记忆体个数越多记忆力越好,但是占用资源更多。
6.9 Embedding 编码
- 独热码:数据量大 过于稀疏,映射之间是独立的,没有表现出关联性。
One-hot编码位宽需要与词汇量一致,词汇量增大时,非常浪费资源。 - Embedding:是一种单词编码方法,用低维向量实现了编码,这种编码通过神经网络训练优化,能表达出单词间的相关性。
自然语言处理中有专门的单词编码。
Embedding 编码API: tf.keras.layers.Embedding(词汇表大小,编码维度)
输入Embedding的x_train维度=[送入样本数, 循环核时间展开步数]
6.10 TensorFlow实现字母预测任务——使用Embedding编码
用RNN实现输入一个字母,预测下一个字母,使用Embedding编码。
# 使x_train符合Embedding输入要求:[送入样本数, 循环核时间展开步数] ,
# 此处整个数据集送入所以送入,送入样本数为len(x_train);输入1个字母出结果,循环核时间展开步数为1。
x_train = np.reshape(x_train, (len(x_train), 1))
y_train = np.array(y_train)
# 在Sequential搭建网络时,增加一层Embedding层。
model = tf.keras.Sequential([
Embedding(5, 2),
SimpleRNN(3),
Dense(5, activation='softmax')
])
# 预测
# 使alphabet符合Embedding输入要求:[送入样本数, 循环核时间展开步数]。
# 此处验证效果送入了1个样本,送入样本数为1;输入1个字母出结果,循环核时间展开步数为1。
alphabet = np.reshape(alphabet, (1, 1))
6.13 长短时记忆网络 (Long Short-Term Memory, LSTM)
LSTM 6 由Hochreiter & Schmidhuber 于1997年提出,通过门控单元改善了传统RNN长期依赖问题。
长期依赖问题
传统的 RNN 会存在长期依赖(Long-Term Dependencies)问题(也称长距离依赖问题),也即是说对于一些时间间隔较长的依赖关系,RNN 会由于自身结构的原因很难学到这种依赖。
比如当模型试着去预测段落“某地开设了大量工厂,空气污染十分严重……这里的天空都是灰色的”的最后一个单词时,仅仅根据短期依赖就无法很好的解决这种问题。因为只根据最后一小段,最后一个词可以是“蓝色的”或者“灰色的”。但如果模型需要预测清楚具体是什么颜色,就需要考虑先前提到但离当前位置较远的上下文信息。因此,当前预测位置和相关信息之间的文本间隔就有可能变得很大。当这个问隔不断增大时,简单的循环神经网络有可能会丧失学习到距离如此远的信息的能力。或者在复杂语言场景中 ,有用信息的间隔有大有小、长短不一 ,循环神经网络的性能也会受到限制。
即传统循环神经网络RNN可以通过记忆体实现 短期记忆 进行连续数据的预测。但是当连续数据的序列变长时,会使展开时间步过长,在反向传播更新参数时,梯度要按时间步连续相乘,会导致梯度消失。长短时记忆网络LSTM 的提出就是为了解决这个问题。
References
周健老师tenserflow课程~
Yann Lecun, Leon Bottou, Y. Bengio, Patrick Haffner. Gradient-Based Learning Applied to Document Recognition. Proceedings of the IEEE, 1998. ↩︎
Alex Krizhevsky, Ilya Sutskever, Geoffrey E. Hinton. ImageNet Classification with Deep Convolutional Neural Networks. In NIPS, 2012. ↩︎
K. Simonyan, A. Zisserman. Very Deep Convolutional Networks for Large-Scale Image Recognition. In ICLR, 2015. ↩︎
Szegedy C, Liu W, Jia Y, et al. Going Deeper with Convolutions. In CVPR, 2015. ↩︎
Kaiming He, Xiangyu Zhang, Shaoqing Ren. Deep Residual Learning for Image Recognition. In CPVR, 2016. ↩︎
Sepp Hochreiter,Jurgen Schmidhuber. LONG SHORT-TERM MEMORY. Neural Computation, December 1997. ↩︎