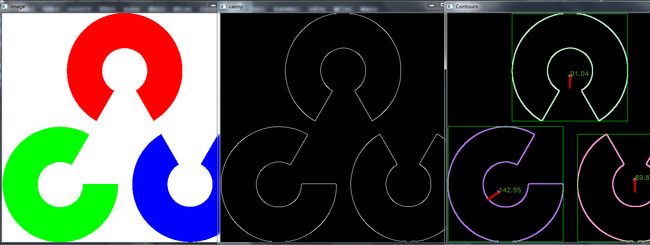
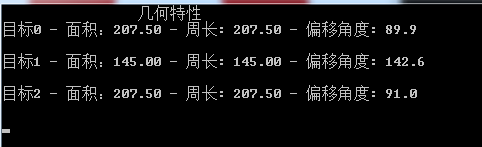
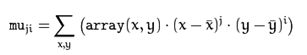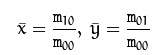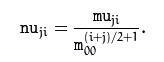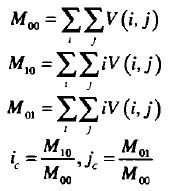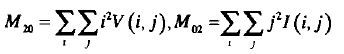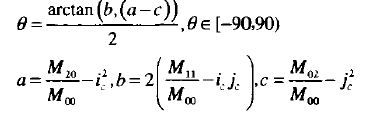【图像处理】轮廓二阶矩计算目标中心-计算目标中心位置方法3

参考 http://blog.csdn.net/yang6464158/article/details/42459595

特征矩的知识在概率论和数理统计中有介绍，空间矩的方法在图像应用中比较广泛，包括零阶矩求面积、一阶矩确定重心、二阶矩确定主方向、二阶矩和三阶矩可以推导出七个不变矩Hu不变矩，不变矩具有旋转，平移、缩放等不变性，因此在工业应用和模式识别中得到广泛的应用。

目标物体灰度函数特征矩的公式定义如下：

如果是二值图像，那么f(x,y)就变成

在OpenCV中，可以很方便的计算多边形区域的3阶特征矩，opencv中的矩主要包括以下几种：空间矩，中心矩和中心归一化矩。

class Moments { public: ...... // 空间矩 double m00, m10, m01, m20, m11, m02, m30, m21, m12, m03;// 中心矩double mu20, mu11, mu02, mu30, mu21, mu12, mu03;// 中心归一化矩 double nu20, nu11, nu02, nu30, nu21, nu12, nu03; }空间矩的公式为：

可以知道，对于01二值化的图像，m00即为轮廓的面积。中心矩的公式为：

其中：

归一化的中心矩公式为：

参考于 链接

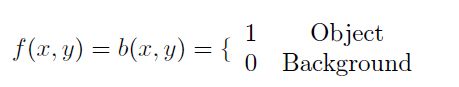
二阶中心距，也叫作方差，它告诉我们一个随机变量在它均值附近波动的大小，方差越大,波动性越大。方差也相当于机械运动中以重心为转轴的转动惯量。(The moment of inertia.)

三阶中心距告诉我们一个随机密度函数向左或向右偏斜的程度。

在均值不为零的情况下，原点距只有纯数学意义。

A1,一阶矩就是 E(X),即样本均值。具体说来就是A1=(西格玛Xi)/n ----（1）
A2,二阶矩就是 E(X^2)即样本平方均值 ,具体说来就是 A2=(西格玛Xi^2)/n-----(2)
Ak,K阶矩就是 E(X^k)即样本K次方的均值,具体说来就是 Ak=(西格玛Xi^k)/n，-----(3)

不变矩的物理含义：
如果把图像看成是一块质量密度不均匀的薄板，其图像的灰度分布函数f(x,y)就是薄板的密度分布函数，则其各阶矩有着不同的含义，如零阶矩表示它的总质量；一阶矩表示它的质心；二阶矩又叫惯性矩，表示图像的大小和方向。事实上，如果仅考虑阶次为2的矩集，则原始图像等同于一个具有确定的大小、方向和离心率，以图像质心为中心且具有恒定辐射率的椭圆。由三阶矩以下矩构成的七个矩不变量具有平移、旋转和尺度不变性等等。当密度分布函数发生改变时，图像的实质没有改变，仍然可以看做一个薄板，只是密度分布有所改变。虽然此时各阶矩的值可能发生变化，但由各阶矩计算出的不变矩仍具有平移、旋转和尺度不变性。通过这个思想，可对图像进行简化处理，保留最能反映目标特性的信息，再用简化后的图像计算不变矩特征，可减少计算量。

研究表明，只有基于二阶矩的不变矩对二维物体的描述才是真正的与旋转、平移和尺度无关的。较高阶的矩对于成像过程中的误差，微小的变形等因素非常敏感，所以相应的不变矩基本上不能用于有效的物体识别。即使是基于二阶矩的不变矩也只能用来识别外形相差特别大的物理，否则他们的不变矩会因为很相似而不能识别。

在OpenCV中，还可以很方便的得到Hu不变距，Hu不变矩在图像旋转、缩放、平移等操作后，仍能保持矩的不变性，所以有时候用Hu不变距更能识别图像的特征。

1、在数学领域，矩 非常的常见
2、在计算机视觉中，使用2维离散形式的矩计算方法
3、使用矩，可以计算物体的面积，物体的质心等。
4、中心矩的计算方法是：某个矩除以0阶矩
5、高阶矩具有旋转不变性，尺度不变性，变换不变性等。

我们很熟悉概率论中的一阶矩二阶矩高阶矩，但是很多人可能和我一样，不明白图像中矩是拿来干嘛的。

在计算机视觉的书中，虽然有提到矩，但是讲的很泛泛也很笼统。自然Google百度这些东西也是靠不牢的。在阅读了相关论文之后，我终于大致对矩在图像中的应用有了了解。

其实矩除了在概率论中有体现，在几何中也是学过的。比方说零阶矩是物体的质量，一阶矩和零阶矩可以算出物体的中心，而二阶矩是用来计算物体的方向的。

拿图像出来来说，图像可以看成是一个平板的物体，其一阶矩和零阶矩就可以拿来计算某个形状的重心，而二阶矩就可以拿来计算形状的方向。

光说不练假把式，下面给出他们的计算公式：

其中M00即零阶矩

M20和M02为二阶矩，接下来计算物体形状的方向



OpenCV代码如下所示：

 #include
 using namespace cv;
 using namespace std;
 Mat src; Mat src_gray;
 int thresh = 30;
 int max_thresh = 255;
 RNG rng(12345);
 int main(){
     src = imread( "opencv-logo.png" ,CV_LOAD_IMAGE_COLOR );
     cvtColor( src, src_gray, CV_BGR2GRAY );//灰度化
     GaussianBlur( src, src, Size(3,3), 0.1, 0, BORDER_DEFAULT );
     blur( src_gray, src_gray, Size(3,3) ); //滤波
     namedWindow( "image", CV_WINDOW_AUTOSIZE );
     imshow( "image", src );
     moveWindow("image",20,20);
     //定义Canny边缘检测图像
     Mat canny_output;
     vector > contours;
     vector hierarchy;
     //利用canny算法检测边缘
     Canny( src_gray, canny_output, thresh, thresh*3, 3 );
     namedWindow( "canny", CV_WINDOW_AUTOSIZE );
     imshow( "canny", canny_output );
     moveWindow("canny",550,20);
     //查找轮廓
     findContours( canny_output, contours, hierarchy, CV_RETR_TREE, CV_CHAIN_APPROX_SIMPLE, Point(0, 0) );
     //计算轮廓矩
     vector mu(contours.size() );
     for( int i = 0; i < contours.size(); i++ )
     { mu[i] = moments( contours[i], false ); }
     //计算轮廓的质心
     vector mc( contours.size() );
     for( int i = 0; i < contours.size(); i++ )
     { mc[i] = Point2d( mu[i].m10/mu[i].m00 , mu[i].m01/mu[i].m00 ); }

     //画轮廓及其质心并显示
     Mat drawing = Mat::zeros( canny_output.size(), CV_8UC3 );
     printf("\t\t 几何特性\n");
     for( int i = 0; i< contours.size(); i++ )
     {
         Scalar color = Scalar( rng.uniform(0, 255), rng.uniform(0,255), rng.uniform(0,255) );
         drawContours( drawing, contours, i, color, 2, 8, hierarchy, 0, Point() );
         circle( drawing, mc[i], 4, color, -1, 8, 0 );
         rectangle(drawing, boundingRect(contours.at(i)), cvScalar(0,255,0));
         printf("目标%d - 面积：%.2f - 周长: %.2f ", i, mu[i].m00, contourArea(contours[i]), arcLength( contours[i], true ) );
         RotatedRect r = fitEllipse(contours.at(i));
         double majorAxis = r.size.height > r.size.width ? r.size.height : r.size.width;//长轴大小
         double minorAxis = r.size.height > r.size.width ? r.size.width : r.size.height;//短轴大小
         double area = mu[i].m00;//面积
         int perimeter = arcLength(contours.at(i), true);
         double orientation = r.angle;
         double orientation_rads = orientation*3.1416/180;
         printf("- 偏移角度: %.1f\n\n", orientation);
         double diameter = sqrt((4*area)/3.1416);//直径
         double eccentricity = sqrt(1-pow(minorAxis/majorAxis,2));//离心率
         double roundness = pow(perimeter, 2)/(2*3.1416*area);//圆滑度
         line(drawing, Point(mc[i].x, mc[i].y), Point(mc[i].x+30*cos(orientation_rads), mc[i].y+30*sin(orientation_rads)), cvScalar(0,0,200), 3);
         char tam[100];
         sprintf(tam, "%.2f", orientation);
         putText(drawing, tam, Point(mc[i].x, mc[i].y), FONT_HERSHEY_SIMPLEX, 0.5, cvScalar(0,220,120),1.5);
     }
     namedWindow( "Contours", CV_WINDOW_AUTOSIZE );
     imshow( "Contours", drawing );
     moveWindow("Contours",1100,20);
     waitKey(0);
     src.release();
     src_gray.release();
     return 0;
 }

结果如下：

计算得到的第二个目标物面积和周长明显不正确，具体原因有待查找

矩、中心矩、质心、patch方向

author@jason_ql 
http://blog.csdn.net/lql0716

---

１、几何矩理论

1.1 矩与数学期望

• 数学期望

定义（一维离散）：设 X∈[a,b] ，密度为 f(x) ，数学期望为： 

E(X)=∑i=1∞xiP(xi)

---

定义（一维连续）：设 X 为连续型随机变量，其概率密度为 f(x) ，则X的数学期望为： 

E(X)=∫+∞−∞xf(x)dx

注：假定广义积分绝对收敛，即 ∫+∞−∞|x|f(x)dx 存在

---

定义（二维离散）：对于离散变量 (X,Y) 的 P(xi,yi) ， PX(xi)=∑jP(xi,yj) 期望为：

E(X)=∑ixiPX(xi)=∑j∑ixiP(xi,yj)

E(Y)=∑jyjPY(yj)=∑j∑iyjP(xi,yj)

---

定义（二维连续）：连续变量 (X,Y) 的 f(x,y) : 

fX(x)=∫+∞−∞f(x,y)dy

E(X)=∫+∞−∞xfX(x)dx=∫+∞−∞x(∫+∞−∞f(x,y)dy)dx=∫+∞−∞∫+∞−∞xf(x,y)dxdy

E(Y)=∫+∞−∞yfY(y)dy=∫+∞−∞∫+∞−∞yf(x,y)dxdy

• 原点矩

定义1：设 X 是随机变量，则称 νk(X)=E(Xk) 为 X 的 k 阶原点矩。

若 X 是离散型随机变量，则：

νk(X)=∑ixkip(xi)

若 X 是连续型随机变量，则：

νk(X)=∫+∞−∞xkf(x)dx

• 中心距

定义2：设 X 是随机变量，则称 

μk(X)=E(X−E(X))k

为 X 的 k 阶 中心距。

若 X 是离散型随机变量，则： 

μk(X)=∑i(xi−E(X))kp(xi)

若 X 是连续型随机变量，则： 

μk(X)=∫+∞−∞(x−E(X))kf(x)dx

• 原点矩与中心距

当中心距中的 E(X) 为0时，此时为 k 阶原点矩，即原点矩是中心距的特殊情况。

一阶原点矩就是数学期望，二阶中心距就是方差，在实际中常用低阶矩，高于四阶矩极少使用。

原点矩与中心距的关系式： 

μ2=ν2−ν21

μ3=ν3−3ν2ν1+2ν31

μ4=ν4−4ν3ν1+6ν2ν21−3ν41

以上可对 μr 用组合数拆开得到。

1.2 图像的矩

把图像的像素看做密度函数 f(x,y) ，对该像素点求期望 E ，即是图像的矩（原点矩）。具体的求解过程参看下面第2节。

一般来说，一阶矩和零阶矩可以计算某个形状的重心，二阶矩可以计算形状的方向。

图像的矩主要表征了图像区域的几何特征，又称几何矩，由于具有旋转、平移、尺度等不变的特兴奋，所以又称为不变矩。 
利用不变矩可以计算出物体的圆形度（物体形状和园的接近程度）、物体的矩形度（物体形状和矩形的接近程度）、物体的水平和垂直对称性、物体的主轴方向、扁度等。

• 原点矩： 
  

  mpq=∑x−1M∑y−1Nxpyqf(x,y)

• 中心距： 
  

  μpq=∑x−1M∑y−1N(x−x0)p(y−y0)qf(x,y)

• 归一化中心距： 
  

  ηpq=μpqμr00
  
  其中 r=p+q+22,p+q=2,3,...

• 一阶矩： 
  见下面第２节．

• 二阶矩：

M20=∑x∑yx2⋅I(x,y)

M02=∑x∑yy2⋅I(x,y)

M11=∑x∑yx⋅y⋅I(x,y)

M20 和 M02 分别表示图像围绕通过重心的垂直和水平轴线的惯性矩。 
M30 和 M03 可以度量图像对于垂直和水平轴线的对称性等。

物体形状的方向： 

θ=arctan(b,(a−c))2=arctan(b/(a−c))2,θ∈[−90。，90。]

其中：

根据一阶矩的质心 C=(M10M00,M01M00) 有

a=M20M00−C20

b=2(M11M00−C0C1)

c=M02M00−C21

2、质心原理

在图像处理中，一阶矩与形状有关，二阶矩显示曲线围绕直线平均值到扩展程度，三阶矩是关于平均值到对称性到测量．由二阶矩和三阶矩可以导出一组共７个不变矩．而不变矩是图像到统计特性，满足平移，伸缩，旋转均不变到不变性．

• moments of a patch(矩): 
  

  mpq=∑x=−r,y=−rrxpyqI(x,y)(1)

• 角点为中心： 
  

  m00=∑x=−r,y=−rrx0y0I(x,y)=∑x=−r,y=−rrI(x,y)(1-1)

• 一阶矩 m01 : 
  

  m01=∑x=−r,y=−rrx0y1I(x,y)=∑x=−r,y=−rry∗I(x,y)(1-2)

• 一阶矩 m10 : 
  

  m10=∑x=−r,y=−rrx1y0I(x,y)=∑x=−r,y=−rrx∗I(x,y)(1-3)

• centroid（质心，亦可称为重心）： 
  

  C=(m10m00,m01m00)(2)
  
  计算质心的优势：对噪声不敏感。当有外部噪声干扰时，计算出的质心不会偏离太大。从数学的角度来看，这种方法是计算一个连通域的质心（或一个团块儿blob的质心）。

• 构造一个向量 OC−→− ,从角点中心 O 到质心 C 。

• orientation of patch（方向）： 
  

  θ=atan2(m01,m10)(3)
  
  建立以角点为圆心的坐标系，如图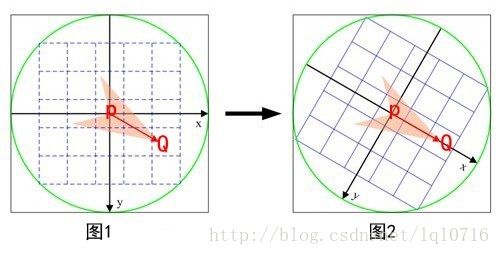 
  在图中， P 为角点，园内为取点区域，每个方格代表一个像素。 
  则质心 Q 可根据式（2）求得。

---

3、中心距函数moments()

• moments()

Calculates all of the moments up to the third order of a polygon or rasterized shape.

C++: Moments moments(InputArray array, bool binaryImage=false )

Python: cv2.moments(array[, binaryImage]) → retval

C: void cvMoments(const CvArr* arr, CvMoments* moments, int binary=0 )

Python: cv.Moments(arr, binary=0) → moments

Parameters: 
array – Raster image (single-channel, 8-bit or floating-point 2D array) or an array ( 1 \times N or N \times 1 ) of 2D points (Point or Point2f ). 
binaryImage – If it is true, all non-zero image pixels are treated as 1’s. The parameter is used for images only. 
moments – Output moments.

• The function computes moments, up to the 3rd order, of a vector shape or a rasterized shape. The results are returned in the structure Moments defined as:

class Moments
{
public:
    Moments();
    Moments(double m00, double m10, double m01, double m20, double m11,
            double m02, double m30, double m21, double m12, double m03 );
    Moments( const CvMoments& moments );
    operator CvMoments() const;

    // spatial moments
    double  m00, m10, m01, m20, m11, m02, m30, m21, m12, m03;
    // central moments
    double  mu20, mu11, mu02, mu30, mu21, mu12, mu03;
    // central normalized moments
    double  nu20, nu11, nu02, nu30, nu21, nu12, nu03;
}
    
    
    
    

     
     
     
     
1
     
     
     
     
2
     
     
     
     
3
     
     
     
     
4
     
     
     
     
5
     
     
     
     
6
     
     
     
     
7
     
     
     
     
8
     
     
     
     
9
     
     
     
     
10
     
     
     
     
11
     
     
     
     
12
     
     
     
     
13
     
     
     
     
14
     
     
     
     
15
     
     
     
     
16
    
    
    
    

---

4、中心矩示例代码

• opencv2.4.13

4.1 C++版代码

#include 
#include 
//  Qt Creator 4.2.0(Based on Qt 5.7.1)
//  OpenCV 2.4.13
using namespace cv;
using namespace std;

#define name1 "原图"
#define name2 "效果图"

cv::Mat img, gray;
int nThresh = 100;
int nMaxThresh = 255;
cv::RNG rng(12345);  //产生一个随机数
cv::Mat cannyImg;
std::vector<std::vector> contours;
std::vector hierarchy;

//void on_ThreshChange( int, void* ){
//    //canny边缘检测
//    cv::Canny( gray, cannyImg, nThresh, nThresh*2, 3 );
//    //找轮廓
//    cv::findContours( cannyImg, contours, hierarchy, cv::RETR_TREE, cv::CHAIN_APPROX_SIMPLE, cv::Point( 0, 0 ) );
//    //计算矩
//    std::vector mu( contours.size() );
//    for(unsigned int i = 0; i < contours.size(); i++){
//        mu[i] = cv::moments( contours[i], false);
//    }
//    //计算中心矩
//    std::vector mc( contours.size() );
//    for( unsigned int i = 0; i < contours.size(); i++ ){
//        mc[i] = cv::Point2f( static_cast(mu[i].m10 / mu[i].m00), static_cast(mu[i].m01 / mu[i].m00));
//    }
//    //画轮廓
//    cv::Mat drawing = cv::Mat::zeros( cannyImg.size(), CV_8UC3);
//    for( unsigned int i = 0; i < contours.size(); i++ ){
//        cv::Scalar color = cv::Scalar( rng.uniform(0, 255), rng.uniform(0, 255), rng.uniform(0, 255) );
//        cv::drawContours( drawing, contours, i, color, 2, 8, hierarchy, 0, cv::Point() );
//        cv::circle( drawing, mc[i], 4, color, -1, 8, 0 );
//    }

//    cv::namedWindow( name2, cv::WINDOW_NORMAL);
//    cv::imshow( name2, drawing );

//    std::cout << "输出内容：　面积和轮廓长度　\n" << std::endl;
//    for(unsigned int i = 0; i < contours.size(); i++ ){
//        std::cout << ">通过ｍ00计算出轮廓[" << i << "]的面积：(M_00) =" << mu[i].m00 << "\n OpenCV 函数计算出的面积　＝　" << cv::contourArea(contours[i]) << "长度：" << cv::arcLength( contours[i], true) <<  "\n\n" << std::endl;
//        cv::Scalar color = cv::Scalar( rng.uniform(0, 255), rng.uniform(0, 255), rng.uniform(0, 255) );
//        cv::drawContours(drawing, contours, i, color, 2, 8, hierarchy, 0, cv::Point() );
//        cv::circle( drawing, mc[i], 4, color, -1, 8, 0 );
//     }
//}


int main(){
    img = cv::imread( "/home/jason/jason2/photo/1.jpg" );
    cv::cvtColor( img, gray, cv::COLOR_BGR2GRAY );
    cv::blur( gray, gray, cv::Size(3, 3) );

    cv::namedWindow( name1, cv::WINDOW_NORMAL );
    cv::imshow( name1, img );

//    cv::createTrackbar( "阈值", name1, &nThresh, nMaxThresh, on_ThreshChange );
//    on_ThreshChange( 0, 0 );

    //canny边缘检测
    cv::Canny( gray, cannyImg, nThresh, nThresh*2, 3 );
    //找轮廓
    cv::findContours( cannyImg, contours, hierarchy, cv::RETR_TREE, cv::CHAIN_APPROX_SIMPLE, cv::Point( 0, 0 ) );
    //计算矩
    std::vector mu( contours.size() );
    for(unsigned int i = 0; i < contours.size(); i++){
        mu[i] = cv::moments( contours[i], false);
    }
    //计算中心矩
    std::vector mc( contours.size() );
    for( unsigned int i = 0; i < contours.size(); i++ ){
        mc[i] = cv::Point2f( static_cast<float>(mu[i].m10 / mu[i].m00), static_cast<float>(mu[i].m01 / mu[i].m00));
    }
    //画轮廓
    cv::Mat drawing = cv::Mat::zeros( cannyImg.size(), CV_8UC3);
    for( unsigned int i = 0; i < contours.size(); i++ ){
        cv::Scalar color = cv::Scalar( rng.uniform(0, 255), rng.uniform(0, 255), rng.uniform(0, 255) );
        cv::drawContours( drawing, contours, i, color, 2, 8, hierarchy, 0, cv::Point() );
        cv::circle( drawing, mc[i], 4, color, -1, 8, 0 );
    }

    cv::namedWindow( name2, cv::WINDOW_NORMAL);
    cv::imshow( name2, drawing );

    std::cout << "输出内容：　面积和轮廓长度　\n" << std::endl;
    for(unsigned int i = 0; i < contours.size(); i++ ){
        std::cout << ">通过ｍ00计算出轮廓[" << i << "]的面积：(M_00) =" << mu[i].m00 << "\n OpenCV 函数计算出的面积　＝　" << cv::contourArea(contours[i]) << "长度：" << cv::arcLength( contours[i], true) <<  "\n\n" << std::endl;
        cv::Scalar color = cv::Scalar( rng.uniform(0, 255), rng.uniform(0, 255), rng.uniform(0, 255) );
        cv::drawContours(drawing, contours, i, color, 2, 8, hierarchy, 0, cv::Point() );
        cv::circle( drawing, mc[i], 4, color, -1, 8, 0 );
     }
    cv::waitKey(0);

    return 0;
}


    
    
    
    

     
     
     
     
原图： 
    
    
    
    

效果图： 

部分打印结果： 

---

4.2 Python版代码

# -*- coding: utf-8 -*-
"""
Created on Sun Mar 26 18:36:19 2017

@author: lql0716
"""

import cv2
import numpy as np

nThresh = 100
nMaxThresh = 255

img = cv2.imread('D:/photo/04.jpg')
gray = cv2.cvtColor(img, cv2.COLOR_RGB2GRAY)
gray = cv2.blur(gray, (3,3))
cv2.namedWindow('img', cv2.WINDOW_NORMAL)
cv2.imshow('img', img)

cannyImg = cv2.Canny(gray, nThresh, nThresh*2, 3)
contours, hierarchy = cv2.findContours(cannyImg, cv2.RETR_TREE, cv2.CHAIN_APPROX_SIMPLE)

mu = []
mc = []
retval = np.array([])
for i in range(0, np.array(contours).shape[0]):
    retval = cv2.moments(contours[i], False)
    mu.append(retval)
mu = np.array(mu)
#print mu[0]['m10']
thetas = []
for i in range(0, np.array(contours).shape[0]):
    if mu[i]['m00'] == 0.0:
        a=0
        b=0
    else:
        a = mu[i]['m10'] / mu[i]['m00']  #质心x坐标
        b = mu[i]['m01'] / mu[i]['m00']  #质心y坐标

        #根据二阶矩计算物体形状的方向
        r1 = mu[i]['m20'] / mu[i]['m00'] - a*a
        r2 = 2.0*(mu[i]['m11'] / mu[i]['m00'] - a*b)
        r3 = mu[i]['m02'] / mu[i]['m00'] - b*b
#        print r1-r3
        if r1-r3==0:
            theta = np.pi / 2
        else:
            theta = np.arctan(r2/(r1-r3)) / 2
        thetas.append(theta)
    mc.append([a,b])
mc = np.array(mc)
drawing = np.zeros(img.shape, dtype = np.uint8)
for i in range(0, mc.shape[0]):
    c1 = np.random.randint(0, 256)
    c2 = np.random.randint(0, 256)
    c3 = np.random.randint(0, 256)
    cv2.drawContours(drawing, contours, i, (c1, c2, c3), 2, 8)
    cv2.circle(drawing, (int(round(mc[i][0])), int(round(mc[i][1]))), 4, (c1, c2, c3), -1, 8, 0)
cv2.namedWindow('img2', cv2.WINDOW_NORMAL)
cv2.imshow('img2', drawing)   
cv2.waitKey(0) 
    
    
    
    

     
     
     
     


    
    
    
    

原图： 

效果图： 

5、Hu矩HuMoments()

原点矩：

mpq=∑x−1M∑y−1Nxpyqf(x,y)

中心距：

μpq=∑x−1M∑y−1N(x−x0)p(y−y0)qf(x,y)

归一化中心距：

ηpq=μpqμr00

其中 r=p+q+22,p+q=2,3,...

当图像变化时， mpq 也变化，而 μpq 具有平移不变形，但对旋转依然敏感。如果用归一化中心距，则可以保持平移不变性、伸缩不变性。

Hu矩利用二阶、三阶中心距构造了7个不变矩，它们在连续图像条件下可保持平移、旋转、伸缩不变，公式如下： 
M1=η20+η02  
M2=(η20−η02)2+4η211  
M3=(η30−3η12)2+(3η21−η03)2  
M4=(η30+η12)2+(η21+η03)2  
M5=(η30−3η12)(η30+η12)((η30+η12)2−3(η21+η03)2)+(3η21−η03)(η21+η03)(3(η30+η12)2−(η21+η03)2)
M6=(η20−η02)((η30+η12)2−(η21+η03)2)+4η11(η30+η12)(η21+η03)  
M7=(3η21−η03)(η30+η12