Lai_im

LeetCode 刷题题目总结

文章目录

前言
LeetCode 总结

整数反转
字符串中的第一个唯一字符
有效的字母异位词
字符串转换整数
实现 strStr()
跳跃游戏
盛最多水的容器
统计「优美子数组」
在排序数组中查找元素的第一个和最后一个位置
搜索二维矩阵
相对名次
旅行终点站
保护城市天际线
砖墙
二叉树的最近公共祖先
顺次数
链表

删除链表中的节点
环形链表
回文链表
合并两个有序链表

滑动窗口

无重复字符的最长子串

BFS & DFS

岛屿数量
二叉树的右视图
找树左下角的值
从上到下打印二叉树 II
N叉树的最大深度
N叉树的层序遍历
从上到下打印二叉树
特定深度节点链表
跳跃游戏 III
二叉树的最小深度
对称的二叉树
二叉树的堂兄弟节点
腐烂的橘子
岛屿的最大面积

回溯算法

全排列
无重复字符串的排列组合
幂集
组合
组合总和 III
分割的回文串
括号生成
电话号码的字母组合
活字印刷
长度为 n 的开心字符串中字典序第 k 小的字符串
黄金矿工

贪心算法

用户分组
跳跃游戏 II

动态规划

最大正方形
统计全为 1 的正方形子矩阵
礼物的最大价值
股票的最大利润
最小路径和
不同路径 II
爬楼梯
和为 K 的子数组

结尾

前言

前段时间参加学校的IT节，然后紧急去刷LeetCode好给自己一个好点点点的排名，结果发现刷题AC还是很有快感的，再加上之前学习了MarkDown就顺带写个刷LeetCode的刷题记录，把自己刷过的希望后面能回顾学习的题目都写下来，好在之后复习复习，现在还是简单中等题为主，嘿嘿，祝自己好运！
有许多题还是勉强过的，还有很多优化空间，所以请各位大佬别在意。

LeetCode 总结

整数反转

给出一个 32 位的有符号整数，你需要将这个整数中每位上的数字进行反转。

示例一：

输入： 123

输出： 321

示例二：

输入： -123

输出： -321

示例三：

输入： 120

输出： 21

这题我的思路是首先将字符串转换为String类型，判断是否为负数，如果是负数的话将符号取出并作标记，然后反转String，最后利用Integer.valueOf()转换回去。

这里踩了个坑，题目输入的是一个 32 位整数，当你输入的这个数足够大，反转后的数可能会大于int的最大值，也可能会小于int的最小值（Integer.MAX_VALUE = -2¹⁵ Integer.MIN_VALUE = 2¹⁵ - 1），所以我们在反转后不能直接将其转换为int类型。

AC代码：

class Solution {
    public int reverse(int x) {
        //将x转换为String类型再进行处理
        String numStr = x + "";
        boolean bool = false;
      	//判断是否为负数
        if (numStr.charAt(0) == '-') {
            numStr = numStr.substring(1);
            bool = true;
        }
        numStr = reStr(numStr);
        
      	//先将其转换为double类型，判断是否超出int的取值范围
        double flag = Double.valueOf(numStr);
        if(flag > Integer.MAX_VALUE || flag < Integer.MIN_VALUE)    return 0;
    
        return bool ? -Integer.valueOf(numStr) : Integer.valueOf(numStr);
    }
    
    public static String reStr(String str) {
        char[] charArr = str.toCharArray();
        
        int left = 0, right = str.length() - 1;
        while (left < right) {
            char temp = charArr[left];
            charArr[left] = charArr[right];
            charArr[right] = temp;
            left++;
            right--;
        }
        
        return String.valueOf(charArr);
    }
}

官方代码：

class Solution {
    public int reverse(int x) {
        int rev = 0;
        while (x != 0) {
            int pop = x % 10;
            x /= 10;
            if (rev > Integer.MAX_VALUE/10 || (rev == Integer.MAX_VALUE / 10 && pop > 7)) return 0;
            if (rev < Integer.MIN_VALUE/10 || (rev == Integer.MIN_VALUE / 10 && pop < -8)) return 0;
            rev = rev * 10 + pop;
        }
        return rev;
    }
}

字符串中的第一个唯一字符

给定一个字符串，找到它的第一个不重复的字符，并返回它的__索引__。如果不存在，则返回 -1。

示例一：

输入： s = “leetcode”

输出： 0

示例二：

输入： s = “loveleetcode”

输出： 2

注意事项： 可以假定该字符串只包含小写字母。

这题我的思路是有Map来储存各个字符的数目，最后再遍历一遍Map找出数量为 1 的字符的返回其下标，否则返回 -1。

AC代码：

class Solution {
    public int firstUniqChar(String s) {
        Map<Character, Integer> map = new HashMap<Character, Integer>();
        
        //map.getOrDefault(key->value, default)
        for (int i = 0; i < s.length(); i++)    
            map.put(s.charAt(i), map.getOrDefault(s.charAt(i), 0) + 1);
        
        for (int i = 0; i < s.length(); i++)
            if(map.get(s.charAt(i)) == 1)
                return i;
        
        return -1;
    }
}

有效的字母异位词

给定两个字符串 s 和 t ，编写一个函数来判断 t 是否是 s 的字母异位词。

示例一：

输入： s = “anagram”, t = “nagaram”

输出： true

示例二：

输入： s = “rat”, t = “car”

输出： false

说明： 可以假设字符串只包含小写字母。

如果 s 和 t 是字母异位词的话，那么它们的各字母个数一定是相等的。

假设字符串中只包含小写字母，创建一个大小为 26 的数组来统计 s 中的各字符个数，再用 t 中的各字符个数减去对应的字符的值，如果最后数组中任意一个值不为 0 ，则说明 s 和 t 不是字母异位词。

AC代码：

class Solution {
    public boolean isAnagram(String s, String t) {
        if (s.length() != t.length())   return false;
        
        int[] cnt = new int[26];
        for (int i = 0; i < s.length(); i++) {
            cnt[s.charAt(i) - 'a']++;
            cnt[t.charAt(i) - 'a']--;
        }
        
        for (int i = 0; i < 26; i++)
            if (cnt[i] != 0) return false;
        
        return true;
    }
}

字符串转换整数

请你来实现一个 atoi 函数，使其能将字符串转换成整数。

首先，该函数会根据需要丢弃无用的开头空格字符，直到寻找到第一个非空格的字符为止。接下来的转化规则如下：

如果第一个非空字符为正或者负号时，则将该符号与之后面尽可能多的连续数字字符组合起来，形成一个有符号整数。

假如第一个非空字符是数字，则直接将其与之后连续的数字字符组合起来，形成一个整数。

该字符串在有效的整数部分之后也可能会存在多余的字符，那么这些字符可以被忽略，它们对函数不应该造成影响。

注意：假如该字符串中的第一个非空格字符不是一个有效整数字符、字符串为空或字符串仅包含空白字符时，则你的函数不需要进行转换，即无法进行有效转换。

在任何情况下，若函数不能进行有效的转换时，请返回 0 。

示例一：

输入： “42”

输出： 42

示例二：

输入： " -42"

输出： -42

示例三：

输入： “4193 with words”

输出： 4193

示例四：

输入： “words and 987”

输出： 0

示例五：

输入： “-91283472332”

输出： -2147483648

提示：

本题中的空白字符只包括空格字符 ' ' 。
假设我们的环境只能存储 32 位大小的有符号整数，那么其数值范围为 [−2³¹, 2³¹ − 1]。如果数值超过这个范围，请返回 INT_MAX (-2³¹ − 1) 或 INT_MIN (−2³¹) 。

我们分情况讨论：

第一个非空字符非数字同时也不是正负号 -> Next。
第一个非空字符为正负号 -> 记录符号。
第一个非空字符为正负数 -> 开始转换。

这里需要注意，在进行转换前总要进行数字的校验，查看转换后数字是否大于 Integer.MAX_VALUE 或小于 Integer.MIN_VALUE ，这里的处理和**「整数反转」**中官方代码的处理方法是一样的。

AC代码：

class Solution {
    public int myAtoi(String str) {
        str = str.trim();
        if (str.length() == 0)  return 0;
        if ((str.charAt(0) < '0' || str.charAt(0) > '9') && str.charAt(0) != '-' && str.charAt(0) != '+') 
            return 0;
        
        boolean bool = false;
        if (str.charAt(0) == '-'){
            bool = true;
            str = str.substring(1);
        }
        else if (str.charAt(0) == '+')
            str = str.substring(1);
        
        int ans = 0;
        for (int i = 0; i < str.length(); i++) {
            if (str.charAt(i) < '0' || str.charAt(i) > '9') break;
            int pop = bool ? -Integer.valueOf(str.charAt(i) - '0') : Integer.valueOf(str.charAt(i) - '0');
            if (ans > Integer.MAX_VALUE / 10 || (ans == Integer.MAX_VALUE / 10 && pop > 7)) return Integer.MAX_VALUE;
            if (ans < Integer.MIN_VALUE / 10 || (ans == Integer.MIN_VALUE / 10 && pop < -8)) return Integer.MIN_VALUE;
            ans = ans * 10 + pop;
        }
        return ans;
    }
}

实现 strStr()

实现 strStr() 函数。

给定一个 haystack 字符串和一个 needle 字符串，在 haystack 字符串中找出 needle 字符串出现的第一个位置 (从0开始)。如果不存在，则返回 -1。

示例一：

输入： haystack = “hello”, needle = “ll”
输出： 2

示例二：

输入： haystack = “aaaaa”, needle = “bba”

输出： -1

说明:

当 needle 是空字符串时，我们应当返回什么值呢？这是一个在面试中很好的问题。

对于本题而言，当 needle 是空字符串时我们应当返回 0 。这与C语言的 strstr() 以及 Java的 indexOf() 定义相符。

滑动窗口。设一个大小为 needle.length()的窗口，从 haystack 的头部开始移动，每次移动都遍历一次，如果满足条件则返回窗口最左端的下标，否则返回 -1。

这里要注意的是如果 needle = “”，则能匹配任何的 haystack 。

AC代码：

class Solution {
    public int strStr(String haystack, String needle) {
        if (needle.length() == 0)   return 0;
        if (haystack.length() < needle.length() || haystack.length() == 0)    return -1;
        
        int left = 0, right = needle.length();
        while (right <= haystack.length()) {
            for (int i = left; i <= right; i++) {
                if (haystack.charAt(i) != needle.charAt(i - left))
                    break;
                if (haystack.charAt(i) == needle.charAt(i - left) && i == right - 1)
                    return left;
            }
            
            left++;
            right++;
        }
        
        return -1;
    }
}

跳跃游戏

给定一个非负整数数组，你最初位于数组的第一个位置。

数组中的每个元素代表你在该位置可以跳跃的最大长度。

判断你是否能够到达最后一个位置。

示例一：

输入： [2,3,1,1,4]

输出： true

示例二：

输入： [3,2,1,0,4]

输出： false

遍历数组，标记你能去到的最右端。

AC代码：

class Solution {
    public boolean canJump(int[] nums) {
        if (nums.length == 1)   return true;
        int last = nums.length - 1;

        int index = nums[0];
        for (int i = 0; i <= index; i++) {
            for (int j = i; j <= i + nums[i]; j++){
                if (j == i) continue;
                if (j + nums[j] >= last)    return true;
                index = Math.max(j + nums[j], index);
            }
        }
        return false;
    }
}

官方代码：

public class Solution {
    public boolean canJump(int[] nums) {
        int n = nums.length;
        int rightmost = 0;
        for (int i = 0; i < n; ++i) {
            if (i <= rightmost) {
                rightmost = Math.max(rightmost, i + nums[i]);
                if (rightmost >= n - 1) {
                    return true;
                }
            }
        }
        return false;
    }
}

盛最多水的容器

给你 n 个非负整数 a₁，a₂，…，a_n，每个数代表坐标中的一个点 (i, a_i) 。在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 (i, a_i) 和 (i, 0)。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

说明：你不能倾斜容器，且 n 的值至少为 2。

示例一：

输入： [1,8,6,2,5,4,8,3,7]

输出： 49

嵌套循环和双指针。

双指针。定义一个 left 指针和一个 right 指针，移动高度更低的一端。

AC代码：

class Solution {
    public int maxArea(int[] height) {
        int ans = 0;
        int left = 0, right = height.length - 1;

        while (left < right) {
            ans = Math.max(ans, (right - left) * Math.min(height[left], height[right]));
            if (height[left] <= height[right])   left++;
            else   right--;
        }

        return ans;
    }
}

class Solution {
    public int maxArea(int[] height) {
        int ans = 0;

        for (int left = 0; left < height.length; left++)
            for (int right = left + 1; right < height.length; right++)
                ans = Math.max(ans, (right - left) * Math.min(height[left], height[right]));

        return ans;
    }
}

统计「优美子数组」

给你一个整数数组 nums 和一个整数 k。

如果某个连续子数组中恰好有 k 个奇数数字，我们就认为这个子数组是「优美子数组」。

请返回这个数组中「优美子数组」的数目。

示例一：

输入： nums = [1,1,2,1,1], k = 3

输出： 2

解释： 包含 3 个奇数的子数组是 [1,1,2,1] 和 [1,2,1,1] 。

示例二：

输入： nums = [2,4,6], k = 1

输出： 0

示例三：

输入： nums = [2,2,2,1,2,2,1,2,2,2], k = 2

输出： 16

其实就是算 k 个奇数数字两边的偶数数字数目，然后将两边的偶数数字数目 + 1再相乘。因为不能确定长度，所以这里用动态数组记录奇数数字两边的偶数数字个数，最后遍历相乘。

AC代码：

class Solution {
    public int numberOfSubarrays(int[] nums, int k) {
        ArrayList<Integer> arr = new ArrayList<>();

        int cnt = 0;
        for (int i = 0; i < nums.length; i++) {
            if (nums[i] % 2 == 0)   ++cnt;
            else {
                arr.add(cnt + 1);
                cnt = 0;
            }
        }
        arr.add(cnt + 1);		//单独处理最后的cnt，不然最后一组的右边偶数数字会漏掉

        int ans = 0;
        int index = 0;
        while (index + k < arr.size()) {
            ans += arr.get(index) * arr.get(index + k);
            index++;
        }

        return ans;
    }
}

在排序数组中查找元素的第一个和最后一个位置

给定一个按照升序排列的整数数组 nums，和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。

你的算法时间复杂度必须是 O(log n) 级别。

如果数组中不存在目标值，返回 [-1, -1]。

示例一：

输入： nums = [5, 7, 7, 8, 8, 10], target = 8

输出： [3, 4]

示例二：

输入： nums = [5, 7, 7, 8, 8, 10], target = 6

输出： [-1, -1]

二分查找的变形。因为是已经按照升序排序的数组，所以二分查找很大的降低时间复杂度。

AC代码：

class Solution {
    public int[] searchRange(int[] nums, int target) {
        int left = 0, right = nums.length - 1;

        while (left <= right) {
            int mid = (left + right) / 2;
            if (nums[mid] == target) {
                int minIndex = mid, maxIndex = mid;
                while (nums[minIndex] == target){
                    minIndex--;
                    if (minIndex < 0)   break;	//	判断是否会越界
                }
                while (nums[maxIndex] == target) {
                    maxIndex++;
                    if (maxIndex >= nums.length)    break;	//	判断是否会越界
                }
                return new int[]{minIndex + 1, maxIndex - 1};
            }   else if (nums[mid] < target) {
                left = mid + 1;
            }   else if (nums[mid] > target) {
                right = mid - 1;
            }
        }

        return new int[]{-1, -1};
    }
}

搜索二维矩阵

编写一个高效的算法来判断 m x n 矩阵中，是否存在一个目标值。该矩阵具有如下特性：

每行中的整数从左到右按升序排列。

每行的第一个整数大于前一行的最后一个整数。

示例一：

输入：

matrix = [
[1, 3, 5, 7],
[10, 11, 16, 20],
[23, 30, 34, 50]
]

target = 3

输出： true

示例二：

输入：

matrix = [
[1, 3, 5, 7],
[10, 11, 16, 20],
[23, 30, 34, 50]
]
target = 13

输出： false

根据这个二维矩阵的两个特性去遍历，尽量做到遍历次数最少。注意要先排除数组的特殊情况再进行下面操作，不然可能会数组越界等等问题。

先判断这个数在哪一行，并记录是第几行。
1. 再遍历相应的那一行找到该数

AC代码：

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        if (matrix.length == 0 || matrix[0].length == 0) return false;

        int row = matrix.length, col = matrix[0].length;
        int cur = 0;

      	//	找到对应的行
        for (int i = 0; i < row; i++) {
            if (target > matrix[i][0] && target < matrix[i][col - 1]){
                cur = i;
                break;
            }   else if (target == matrix[i][0] || target == matrix[i][col - 1]) {
                return true;
            }
        }
				//	根据行号找target
        for (int i = 0; i < col; i++)
            if (matrix[cur][i] == target)   return true;

        return false;
    }
}

相对名次

给出 N 名运动员的成绩，找出他们的相对名次并授予前三名对应的奖牌。前三名运动员将会被分别授予 “金牌”，“银牌” 和“ 铜牌”（“Gold Medal”, “Silver Medal”, “Bronze Medal”）。

(注：分数越高的选手，排名越靠前。)

示例一：

输入： [5, 4, 3, 2, 1]

输出： [“Gold Medal”, “Silver Medal”, “Bronze Medal”, “4”, “5”]

解释： 前三名运动员的成绩为前三高的，因此将会分别被授予 “金牌”，“银牌”和“铜牌” (“Gold Medal”, “Silver Medal” and “Bronze Medal”).
余下的两名运动员，我们只需要通过他们的成绩计算将其相对名次即可。

提示:

N 是一个正整数并且不会超过 10000。
所有运动员的成绩都不相同。

二分查找降低时间复杂度。先复制一个数组然后排序，用二分查找去查找名次。

AC代码：

class Solution {
    public String[] findRelativeRanks(int[] nums) {
        int[] sort = nums.clone();
        Arrays.sort(sort);
        String[] ans = new String[nums.length];

        int index = 0;
        for (int i = 0; i < nums.length; i++) {
            int rank = binSearch(sort, nums[i]) + 1;
            if (rank == nums.length)   ans[index++] = "Gold Medal";
            else if (rank == nums.length - 1)   ans[index++] = "Silver Medal";
            else if (rank == nums.length - 2)   ans[index++] = "Bronze Medal";
            else    ans[index++] = nums.length - rank + 1 + "";
        }

        return ans;
    }
    int binSearch(int[] sort, int target) {
        int left = 0, right = sort.length - 1;
        while (left <= right) {
            int mid = (left + right) / 2;
            if (sort[mid] == target)    return mid;
            else if (sort[mid] < target)    left = mid + 1;
            else if (sort[mid] > target)    right = mid - 1;
        }

        return -1;
    }
}

旅行终点站

给你一份旅游线路图，该线路图中的旅行线路用数组 paths 表示，其中 paths[i] = [cityAi, cityBi] 表示该线路将会从 cityAi 直接前往 cityBi 。请你找出这次旅行的终点站，即没有任何可以通往其他城市的线路的城市。

题目数据保证线路图会形成一条不存在循环的线路，因此只会有一个旅行终点站。

示例一：

输入： paths = [[“London”,“New York”],[“New York”,“Lima”],[“Lima”,“Sao Paulo”]]

输出： “Sao Paulo”

解释： 从 “London” 出发，最后抵达终点站 “Sao Paulo” 。本次旅行的路线是 “London” -> “New York” -> “Lima” -> “Sao Paulo” 。

示例二：

输入： paths = [[“B”,“C”],[“D”,“B”],[“C”,“A”]]

输出： “A”

解释：

所有可能的线路是：
“D” -> “B” -> “C” -> “A”.
“B” -> “C” -> “A”.
“C” -> “A”.
“A”.

示例三：

输入： paths = [[“A”,“Z”]]

输出： “Z”

找到一个没有出度的节点。用一个Set把所有起点站存进去，然后遍历所有终点站，如果这个站点不包含在Set里，那这个站就是终点站。

AC代码：

class Solution {
    public String destCity(List<List<String>> paths) {
        Set<String> city = new HashSet<>();
        for (List<String> start: paths)
            city.add(start.get(0));

        for (List<String> end: paths)
            if (!city.contains(end.get(1)))  return end.get(1);

        return "";
    }
}

保护城市天际线

在二维数组grid中，grid[i][j]代表位于某处的建筑物的高度。我们被允许增加任何数量（不同建筑物的数量可能不同）的建筑物的高度。高度 0 也被认为是建筑物。

最后，从新数组的所有四个方向（即顶部，底部，左侧和右侧）观看的“天际线”必须与原始数组的天际线相同。城市的天际线是从远处观看时，由所有建筑物形成的矩形的外部轮廓。请看下面的例子。

建筑物高度可以增加的最大总和是多少？

示例一：

输入： grid = [[3,0,8,4],[2,4,5,7],[9,2,6,3],[0,3,1,0]]

输出： 35

解释：

The grid is:
[ [3, 0, 8, 4],
[2, 4, 5, 7],
[9, 2, 6, 3],
[0, 3, 1, 0] ]

从数组竖直方向（即顶部，底部）看“天际线”是：[9, 4, 8, 7]
从水平水平方向（即左侧，右侧）看“天际线”是：[8, 7, 9, 3]

在不影响天际线的情况下对建筑物进行增高后，新数组如下：

gridNew = [ [8, 4, 8, 7],
[7, 4, 7, 7],
[9, 4, 8, 7],
[3, 3, 3, 3] ]

说明：

1 < grid.length = grid[0].length <= 50。

grid[i][j] 的高度范围是： [0, 100]。

一座建筑物占据一个grid[i][j]：换言之，它们是 1 x 1 x grid[i][j] 的长方体。

用两个数组分别存储水平和竖直方向的最高高度，最后遍历作差。

AC代码：

class Solution {
    public int maxIncreaseKeepingSkyline(int[][] grid) {
        int[] row = new int[grid.length], col = new int[grid[0].length];

        for (int i = 0; i < grid.length; i++) {
            int max = 0;
            for (int j = 0; j < grid[i].length; j++)
                max = Math.max(max, grid[i][j]);
            row[i] = max;
        }
        for (int i = 0; i < grid[0].length; i++) {
            int max = 0;
            for (int j = 0; j < grid.length; j++)
                max = Math.max(max, grid[j][i]);
            col[i] = max;
        }

        int res = 0;
        for (int i = 0; i < grid.length; i++) {
            for (int j = 0; j < grid[i].length; j++) {
                if (grid[i][j] == row[i] || grid[i][j] == col[j])   continue;
                res += Math.min(row[i], col[j]) - grid[i][j];
            }
        }

        return res;
    }
}

砖墙

你的面前有一堵方形的、由多行砖块组成的砖墙。这些砖块高度相同但是宽度不同。你现在要画一条自顶向下的、穿过最少砖块的垂线。

砖墙由行的列表表示。每一行都是一个代表从左至右每块砖的宽度的整数列表。

如果你画的线只是从砖块的边缘经过，就不算穿过这块砖。你需要找出怎样画才能使这条线穿过的砖块数量最少，并且返回穿过的砖块数量。

你不能沿着墙的两个垂直边缘之一画线，这样显然是没有穿过一块砖的。

示例一：

输入： [[1,2,2,1],
[3,1,2],
[1,3,2],
[2,4],
[3,1,2],
[1,3,1,1]]

输出： 2

解释：

提示：

每一行砖块的宽度之和应该相等，并且不能超过 INT_MAX。
每一行砖块的数量在 [1,10,000] 范围内，墙的高度在 [1,10,000] 范围内，总的砖块数量不超过 20,000。

Map存储每一行添加每一块砖后的长度。最后遍历Map取最大值就是能穿过的最大砖块数量，返回行数 - 能穿过的最大砖块数。

AC代码：

class Solution {
    public int leastBricks(List<List<Integer>> wall) {
        Map<Integer, Integer> map = new HashMap<>();
        for (List<Integer> row: wall) {
            int cur = 0;
            for (int i = 0; i < row.size() - 1; i++) {	//	最后一个砖块不计入
                cur += row.get(i);
                map.put(cur, map.getOrDefault(cur, 0) + 1);
            }
        }

        int max = 0;
        for (int v: map.values())   max = Math.max(max, v);

        return wall.size() - max;
    }
}

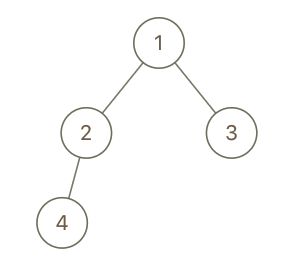
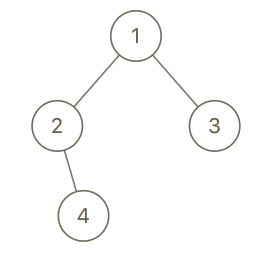
二叉树的最近公共祖先

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

示例一：

输入： root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1

输出： 3

解释： 节点 5 和节点 1 的最近公共祖先是节点 3。

示例二：

输入： root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4

输出： 5

解释： 节点 5 和节点 4 的最近公共祖先是节点 5。因为根据定义最近公共祖先节点可以为节点本身。

用Map记录一个节点的父点，用Set保存访问过的父节点。如果该父节点已经被访问过了，那此节点就是最近的公共祖先。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    Map<Integer, TreeNode> parent = new HashMap<>();
    Set<Integer> visited = new HashSet<>();
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        BFS(root);
        while (p != null) {
            visited.add(p.val);
            p = parent.get(p.val);
        }
        while (q != null) {
            if (visited.contains(q.val))    return q;
            q = parent.get(q.val);
        }

        return null;
        
    }
    void BFS(TreeNode root) {
        if (root.left != null) {
            parent.put(root.left.val, root);
            BFS(root.left);
        }
        if (root.right != null) {
            parent.put(root.right.val, root);
            BFS(root.right);
        }
    }
}

顺次数

我们定义「顺次数」为：每一位上的数字都比前一位上的数字大 1 的整数。

请你返回由 [low, high] 范围内所有顺次数组成的有序列表（从小到大排序）。

示例一：

输入： low = 100, high = 300

输出： [123,234]

示例二：

输入： low = 1000, high = 13000

输出： [1234,2345,3456,4567,5678,6789,12345]

枚举。

AC代码：

class Solution {
    public List<Integer> sequentialDigits(int low, int high) {
        List<Integer> res = new ArrayList<>();
        for (int i = 1; i <= 9; i++) {
            int num = i;
            for (int j = i + 1; j <= 9; j++) {
                num = num * 10 + j;
                if (num >= low && num <= high)  res.add(num);
            }
        }
        
        Collections.sort(res);
        return res;
    }
}

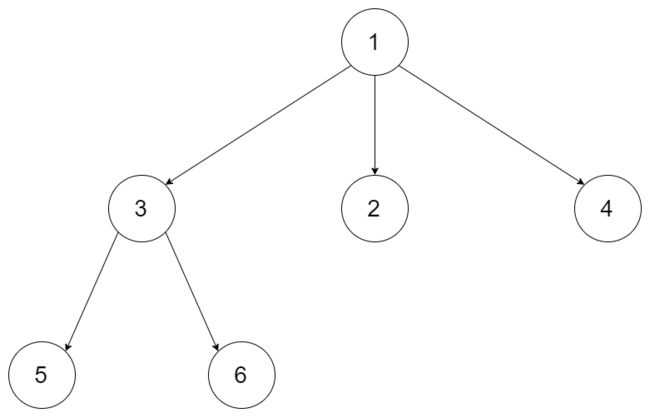
链表

删除链表中的节点

请编写一个函数，使其可以删除某个链表中给定的（非末尾）节点，你将只被给定要求被删除的节点。

现有一个链表 – head = [4,5,1,9]，它可以表示为:

示例一：

输入： head = [4,5,1,9], node = 5

输出： [4,1,9]

示例二：

输入： head = [4,5,1,9], node = 1

输出： [4,5,9]

说明:

链表至少包含两个节点。
链表中所有节点的值都是唯一的。
给定的节点为非末尾节点并且一定是链表中的一个有效节点。
不要从你的函数中返回任何结果。

题目给这个节点就是你需要修改的节点而不是链表的头节点，而且此链表是单向链表，无法向单向链表一样操作。所以我们将当前这个节点的值修改为下一个节点的值，再将当前节点链接到下下个节点，就可以完成删除当前节点的操作了。

AC代码：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    void deleteNode(ListNode* node) {
        node->val = node->next->val;
        node->next = node->next->next;
    }
};

环形链表

给定一个链表，判断链表中是否有环。

为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。

示例一：

输入： head = [3,2,0,-4], pos = 1

输出： true

示例二：

输入： head = [1,2], pos = 0

输出： true

示例三：

输入： head = [1], pos = -1

输出： false

简单的快慢指针。定义一个快指针和一个慢指针，快指针每次循环走 2 步，慢指针每次循环走 1 步，当两个指针相遇时，代表链表有环。

AC代码：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    bool hasCycle(ListNode *head) {
        ListNode *slow = head;
        ListNode *fast = head;
        
        while (fast && fast->next) {
            fast = fast->next->next;
            slow = slow->next;
            if (fast == slow)   return true;
        }
        
        return false;
    }
};

回文链表

请判断一个链表是否为回文链表。

示例一：

输入： 1->2

输出： false

示例二：

输入： 1->2->2->1

输出： true

利用栈先遍历一次链表，然后判断是否是回文链表。

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
    public boolean isPalindrome(ListNode head) {
        Stack<Integer> stack = new Stack<>();
        ListNode p = head;

        while (p != null) {
            stack.push(p.val);
            p = p.next;
        }

        boolean bool = true;
        while (!stack.isEmpty()) {
            if (stack.pop() != head.val) {
                bool = false;
                break;
            }
            head = head.next;
        }

        return bool;
    }
}

合并两个有序链表

将两个升序链表合并为一个新的升序链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。

示例一：

输入： 1->2->4, 1->3->4

输出： 1->1->2->3->4->4

AC代码：

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
    public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
        ListNode perHead = new ListNode(0);

        ListNode head = perHead;
        while (l1 != null && l2 != null) {
            if (l1.val < l2.val) {
                ListNode p = new ListNode(l1.val);
                l1 = l1.next;
                head.next = p;
            }
            else {
                ListNode p = new ListNode(l2.val);
                l2 = l2.next;
                head.next = p;
            }
            head = head.next;
        }
        while (l1 != null) {
            ListNode p = new ListNode(l1.val);
            l1 = l1.next;
            head.next = p;
            head = head.next;
        }
        while (l2 != null) {
            ListNode p = new ListNode(l2.val);
            l2 = l2.next;
            head.next = p;
            head = head.next;
        }

        return perHead.next;
    }
}

官方代码：

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
    public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
        ListNode perHead = new ListNode(0);

        ListNode pre = perHead;
        while (l1 != null && l2 != null) {
            if (l1.val < l2.val) {
                pre.next = l1;
                l1 = l1.next;
            }
            else {
                pre.next = l2;
                l2 = l2.next;
            }
            pre = pre.next;
        }
        if (l1 != null) pre.next = l1;
        else    pre.next = l2;

        return perHead.next;
    }
}

滑动窗口

无重复字符的最长子串

给定一个字符串，请你找出其中不含有重复字符的 最长子串 的长度。

示例一：

输入： “abcabcbb”

输出： 3

解释： 因为无重复字符的最长子串是 “abc”，所以其长度为 3。

示例二：

输入： “bbbbb”

输出： 1

示例三：

输入： “pwwkew”

输出： 3

解释： 因为无重复字符的最长子串是 “wke”，所以其长度为 3。
请注意，你的答案必须是子串的长度，“pwke” 是一个子序列，不是子串。

AC代码：

class Solution {
    public int lengthOfLongestSubstring(String s) {
        List<Character> cur = new ArrayList<>();
        int max = 0;
        int left = 0, right = 0;
        while (right < s.length()) {
            if (!cur.contains(s.charAt(right))) {
                cur.add(s.charAt(right));
                right++;
            }
            else if (cur.contains(s.charAt(right))) {
                max = Math.max(max, cur.size());
                while (cur.contains(s.charAt(right))) {
                    cur.remove((Object)(s.charAt(left)));
                    left++;
                }
            }
        }
        while (left < s.length()) {
            if (cur.contains(s.charAt(right - 1))) {
                max = Math.max(max, cur.size());
                while (cur.contains(s.charAt(right - 1))) {
                    cur.remove((Object)(s.charAt(left)));
                    left++;
                }
            }
        }

        return max;
    }
}

BFS & DFS

岛屿数量

给你一个由 ‘1’（陆地）和 ‘0’（水）组成的的二维网格，请你计算网格中岛屿的数量。

岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。

此外，你可以假设该网格的四条边均被水包围。

示例一：

输入：

11110

11010

11000

00000

输出： 1

示例二：

输入：

11000

11000

00100

00011

输出： 3

BFS 和 DFS 。

AC代码：

class Solution {
    int[][] dl = {{-1, 0}, {0, -1}, {0, 1}, {1, 0}};
    int ans = 0;
    public int numIslands(char[][] grid) {
        if (grid == null || grid.length == 0)   return 0;

        int row = grid.length, col = grid[0].length;
        boolean[][] visits = new boolean[row][col];
        ans = 0;

        for (int i = 0; i < row; i++)
            for (int j = 0; j < col; j++) 
                if (!visits[i][j] && grid[i][j] == '1') {
                    BFS(grid, visits, i, j);
                    ans++;
                }

        return ans;
    }
    public void BFS(char[][] grid, boolean[][] visits, int row, int col) {
        if (grid[row][col] == '1' && !visits[row][col]) {
            visits[row][col] = true;
            for (int k = 0; k < 4; k++) {
                if (row + dl[k][0] >= 0 && row + dl[k][0] < grid.length && col + dl[k][1] >= 0 && col + dl[k][1] < grid[row].length)  
                  	BFS(grid, visits, row + dl[k][0], col + dl[k][1]);
            }
        }

    }
}

官方代码：

//	DFS
class Solution {
    void dfs(char[][] grid, int r, int c) {
        int nr = grid.length;
        int nc = grid[0].length;

        if (r < 0 || c < 0 || r >= nr || c >= nc || grid[r][c] == '0') {
            return;
        }

        grid[r][c] = '0';
        dfs(grid, r - 1, c);
        dfs(grid, r + 1, c);
        dfs(grid, r, c - 1);
        dfs(grid, r, c + 1);
    }

    public int numIslands(char[][] grid) {
        if (grid == null || grid.length == 0) {
            return 0;
        }

        int nr = grid.length;
        int nc = grid[0].length;
        int num_islands = 0;
        for (int r = 0; r < nr; ++r) {
            for (int c = 0; c < nc; ++c) {
                if (grid[r][c] == '1') {
                    ++num_islands;
                    dfs(grid, r, c);
                }
            }
        }

        return num_islands;
    }
}

//	BFS
class Solution {
    public int numIslands(char[][] grid) {
        if (grid == null || grid.length == 0) {
            return 0;
        }

        int nr = grid.length;
        int nc = grid[0].length;
        int num_islands = 0;

        for (int r = 0; r < nr; ++r) {
            for (int c = 0; c < nc; ++c) {
                if (grid[r][c] == '1') {
                    ++num_islands;
                    grid[r][c] = '0';
                    Queue<Integer> neighbors = new LinkedList<>();
                    neighbors.add(r * nc + c);
                    while (!neighbors.isEmpty()) {
                        int id = neighbors.remove();
                      	//	
                        int row = id / nc;
                        int col = id % nc;
                        if (row - 1 >= 0 && grid[row-1][col] == '1') {
                            neighbors.add((row-1) * nc + col);
                            grid[row-1][col] = '0';
                        }
                        if (row + 1 < nr && grid[row+1][col] == '1') {
                            neighbors.add((row+1) * nc + col);
                            grid[row+1][col] = '0';
                        }
                        if (col - 1 >= 0 && grid[row][col-1] == '1') {
                            neighbors.add(row * nc + col-1);
                            grid[row][col-1] = '0';
                        }
                        if (col + 1 < nc && grid[row][col+1] == '1') {
                            neighbors.add(row * nc + col+1);
                            grid[row][col+1] = '0';
                        }
                    }
                }
            }
        }

        return num_islands;
    }
}

二叉树的右视图

给定一棵二叉树，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。

也是DFS和BFS。

AC代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int dep = -1;	//	记录最深深度

  	/**
  		root	当前节点
  		ans	记录节点
  		cur	当前节点的深度
  	*/
    void visTreeNode(TreeNode* root, vector<int>& ans, int cur) {
        if (!root)  return;

      	//	如果当前深度大于之前的深度
        if (cur > dep){
            dep = cur;	//	修正深度
            ans.push_back(root->val);
        }
        visTreeNode(root->right, ans, cur + 1);	//先访问右子树
        visTreeNode(root->left, ans, cur + 1);
    }
    vector<int> rightSideView(TreeNode* root) {
        vector<int> ans;

        visTreeNode(root, ans, 0);

        return ans;
    }
};

官方代码：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public List<Integer> rightSideView(TreeNode root) {
        ArrayList<Integer> ans = new ArrayList<>();
        if (root == null)   return ans;

        Queue<TreeNode> queue = new LinkedList<>();	//	队列记录当前层数的节点
        queue.offer(root);	//	先将根节点入队

        while (!queue.isEmpty()) {
            int size = queue.size();	//当前层数节点的个数
            for (int i = 0; i < size; i++) {	//	遍历当前层数的所有节点
                TreeNode cur = queue.poll();
                
                if (cur.left != null)  queue.offer(cur.left);
                if (cur.right != null)  queue.offer(cur.right);
                if (i == size - 1)  ans.add(cur.val);	//	加入最右边的节点的val
            }
        }

        return ans;
    }
}

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    ArrayList<Integer> ans = new ArrayList<>();
    public List<Integer> rightSideView(TreeNode root) {
        DFS(root, 0);

        return ans;
    }

    public void DFS(TreeNode root, int dep) {
        if (root == null)   return;

        if (dep == ans.size())  ans.add(root.val);
        dep++;

        DFS(root.right, dep);
        DFS(root.left, dep);
    }
}

找树左下角的值

给定一个二叉树，在树的最后一行找到最左边的值。

示例一：

输入：

2

/ \

1 3

输出： 1

示例二：

输入：

1

/ \

2 3

/ / \

4 5 6

/

7

输出： 7

BFS。

AC代码：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public int findBottomLeftValue(TreeNode root) {
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        int lastVal = root.val;

        while (!queue.isEmpty()) {
            int size = queue.size();
            for (int i = 0; i < size; i++) {
                TreeNode cur = queue.poll();
                if (i == 0) lastVal = cur.val;
                if (cur.left != null)  queue.offer(cur.left);	//	先遍历左子树
                if (cur.right != null) queue.offer(cur.right);
            }
        }

        return lastVal;
    }
}

从上到下打印二叉树 II

从上到下按层打印二叉树，同一层的节点按从左到右的顺序打印，每一层打印到一行。

BFS。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> res = new ArrayList<>();
        Queue<TreeNode> queue = new LinkedList<>();
        
        if (root != null)   queue.offer(root);
        while (!queue.isEmpty()) {
            List<Integer> list = new ArrayList<>();
            int size = queue.size();
            for (int i = 0; i < size; i++) {
                TreeNode cur = queue.poll();
                list.add(cur.val);

                if (cur.left != null)   queue.offer(cur.left);
                if (cur.right != null)  queue.offer(cur.right);
            }
            res.add(new ArrayList(list));
        }

        return res;
    }
}

N叉树的最大深度

给定一个 N 叉树，找到其最大深度。

最大深度是指从根节点到最远叶子节点的最长路径上的节点总数。

输入：

输出： 3

说明:

树的深度不会超过 1000。
树的节点总不会超过 5000。

AC代码：

/*
// Definition for a Node.
class Node {
    public int val;
    public List children;

    public Node() {}

    public Node(int _val) {
        val = _val;
    }

    public Node(int _val, List _children) {
        val = _val;
        children = _children;
    }
};
*/

class Solution {
    public int maxDepth(Node root) {
        Queue<Node> queue = new LinkedList<>();
        if (root != null)   queue.offer(root);
        else return 0;
        int ans = 1;

        while (!queue.isEmpty()) {
            int size = queue.size();
            boolean bool = false;
            for (int i = 0; i < size; i++) {
                Node cur = queue.poll();
                for (int j = 0; j < cur.children.size(); j++) {
                    queue.offer(cur.children.get(j));
                    bool = true;
                }
            }
            if (bool)   ans++;
        }

        return ans;
    }
}

N叉树的层序遍历

给定一个 N 叉树，返回其节点值的层序遍历。 (即从左到右，逐层遍历)。

输入：

输出：

[

[1],

[3, 2, 4],

[5, 6]

]

从上到下打印二叉树

从上到下打印出二叉树的每个节点，同一层的节点按照从左到右的顺序打印。

基础遍历二叉树的问题。

AC代码：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public int[] levelOrder(TreeNode root) {
        if (root == null)   return new int[]{};

        List<Integer> list = new ArrayList<>();
        Queue<TreeNode> queue = new LinkedList<>();

        queue.offer(root);
        while (!queue.isEmpty()) {
            int size = queue.size();
            for (int i = 0; i < size; i++) {
                TreeNode cur = queue.poll();
                list.add(cur.val);

                if (cur.left != null)   queue.offer(cur.left);
                if (cur.right != null)  queue.offer(cur.right);
            }
        }

        int[] ans = new int[list.size()];
        for (int i = 0; i < list.size(); i++)
            ans[i] = list.get(i);

        return ans;
    }
}

特定深度节点链表

给定一棵二叉树，设计一个算法，创建含有某一深度上所有节点的链表（比如，若一棵树的深度为 D，则会创建出 D 个链表）。返回一个包含所有深度的链表的数组。

示例一：

输入： [1,2,3,4,5,null,7,8]
        1
       /  \ 
      2    3
     / \    \ 
    4   5    7
   /
  8
输出： [[1],[2,3],[4,5,7],[8]]

题目要求返回链表数组。

AC代码：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
    public ListNode[] listOfDepth(TreeNode tree) {
        List<ListNode> res = new ArrayList<>();	//	链表数组
        if (tree == null)   return new ListNode[]{};

        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(tree);

        while (!queue.isEmpty()) {
            int size = queue.size();
            ListNode head = null;	//	头节点初始化
            for (int i = 0; i < size; i++) {
                TreeNode cur = queue.poll();
                if (i == 0) {
                    head = new ListNode(cur.val);
                    res.add(head);
                }
                else {
                    head.next = new ListNode(cur.val);
                    head = head.next;
                }
                
              	//	层序遍历先左子树再右子树
                if (cur.left != null)   queue.offer(cur.left);
                if (cur.right != null)  queue.offer(cur.right);
            }
        }

        return res.toArray(new ListNode[res.size()]);
    }
}

跳跃游戏 III

这里有一个非负整数数组 arr，你最开始位于该数组的起始下标 start 处。当你位于下标 i 处时，你可以跳到 i + arr[i] 或者 i - arr[i]。

请你判断自己是否能够跳到对应元素值为 0 的任意下标处。

注意，不管是什么情况下，你都无法跳到数组之外。

示例一：

输入： arr = [4,2,3,0,3,1,2], start = 5

输出： true

解释：
到达值为 0 的下标 3 有以下可能方案：
下标 5 -> 下标 4 -> 下标 1 -> 下标 3
下标 5 -> 下标 6 -> 下标 4 -> 下标 1 -> 下标 3

示例二：

输入： arr = [4,2,3,0,3,1,2], start = 0

输出： true

解释：

到达值为 0 的下标 3 有以下可能方案：
下标 0 -> 下标 4 -> 下标 1 -> 下标 3

示例三：

输入： arr = [3,0,2,1,2], start = 2

输出： false

简单的BFS。

AC代码：

class Solution {
    boolean bool = false;
    public boolean canReach(int[] arr, int start) {
        boolean[] visited = new boolean[arr.length];	//	记录被访问的数字防止超时
        BFS(arr, start, visited);

        return bool;
    }
    void BFS(int[] arr, int start, boolean[] visited) {
        if (arr[start] == 0) { 
            bool = true;
            return;
        }
        if (visited[start]) return;
        visited[start] = true;

        if (start + arr[start] < arr.length)    BFS(arr, start + arr[start], visited);
        if (start - arr[start] >= 0)    BFS(arr, start - arr[start], visited);
    }
}

二叉树的最小深度

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明: 叶子节点是指没有子节点的节点。

我发现只要一天不练简单的BFS问题，就直接自闭了。

AC代码：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public int minDepth(TreeNode root) {
        if (root == null)   return 0;
        int minDepth = 0;
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        boolean bool = true;

        while (!queue.isEmpty() && bool) {
            int size = queue.size();
            minDepth++;
            for (int i = 0; i < size; i++) {
                TreeNode cur = queue.poll();
                if (cur.left == null && cur.right == null) {
                    bool = false;
                    break;
                }
                if (cur.left != null)   queue.offer(cur.left);
                if (cur.right != null)  queue.offer(cur.right);
            }
        }

        return minDepth;
    }
}

对称的二叉树

给定一个二叉树，检查它是否是镜像对称的。

示例一：

输入： [1,2,2,3,4,4,3]
    1
   / \
  2   2
 / \ / \
3  4 4  3
输出： true

示例二：

输入： [1,2,2,null,3,null,3]
    1
   / \
  2   2
   \   \
   3    3
输出： false

AC代码：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public boolean isSymmetric(TreeNode root) {
        if (root == null)   return true;

        List<TreeNode> list = new ArrayList<>();
        list.add(root);
        while (!list.isEmpty()) {
            int size = list.size();
            int left = 0, right = size - 1;
            List<TreeNode> cur = new ArrayList<>();
            while (left <= right) {
                if (list.get(left).left != null && list.get(right).right == null || list.get(left).left == null && list.get(right).right != null || list.get(left).right == null && list.get(right).left != null || list.get(left).right != null && list.get(right).left == null)   return false;

                if (list.get(left).left != null && list.get(right).right != null)
                    if (list.get(left).left.val != list.get(right).right.val)   return false;
                if (list.get(left).right != null && list.get(right).left != null)
                    if (list.get(left).right.val != list.get(right).left.val)   return false;
                left++;
                right--;
            }
            for (int i = 0; i < size; i++) {
                if (list.get(i).left != null)   cur.add(list.get(i).left);
                if (list.get(i).right != null)  cur.add(list.get(i).right);
            }
            list.clear();
            list.addAll(cur);
            cur.clear();
        }

        return true;
    }
}

官方代码：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public boolean isSymmetric(TreeNode root) {
        if (root == null)   return true;

        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        queue.offer(root);
        while (!queue.isEmpty()) {
            int size = queue.size();
            for (int i = 0; i < size; i++) {
                TreeNode t1 = queue.poll();
                TreeNode t2 = queue.poll();

                if (t1 == null && t2 == null)   continue;
                if (t1 == null || t2 == null)   return false;
                if (t1.val != t2.val)   return false;

                queue.offer(t1.left);
                queue.offer(t2.right);
                queue.offer(t1.right);
                queue.offer(t2.left);
            }
        }

        return true;
    }
}

二叉树的堂兄弟节点

在二叉树中，根节点位于深度 0 处，每个深度为 k 的节点的子节点位于深度 k+1 处。

如果二叉树的两个节点深度相同，但父节点不同，则它们是一对堂兄弟节点。

我们给出了具有唯一值的二叉树的根节点 root，以及树中两个不同节点的值 x 和 y。

只有与值 x 和 y 对应的节点是堂兄弟节点时，才返回 true。否则，返回 false。

示例一：

输入： root = [1,2,3,4], x = 4, y = 3

输出： false

示例三：

输入： root = [1,2,3,null,4], x = 2, y = 3

输出： false

提示：

二叉树的节点数介于 2 到 100 之间。
每个节点的值都是唯一的、范围为 1 到 100 的整数。

BFS。如果是堂兄弟节点那么在一个根不能同时包含 x 和 y 两个数，但在同一深度下包含 x 和 y ，只需考虑这两种情况就可以了。

AC代码：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public boolean isCousins(TreeNode root, int x, int y) {
        Queue<TreeNode> queue = new LinkedList<>();
        List<Integer> list = new ArrayList<>();
        queue.offer(root);

        while (!queue.isEmpty()) {
            int size = queue.size();
            for (int i = 0; i < size; i++) {
                TreeNode cur = queue.poll();
                List<Integer> curVal = new ArrayList<>();

                if (cur.left != null) {
                    queue.offer(cur.left);
                    curVal.add(cur.left.val);
                }
                if (cur.right != null) {
                    queue.offer(cur.right);
                    curVal.add(cur.right.val);
                }
                if (curVal.contains(x) && curVal.contains(y)) return false;	//	如果在 x 和 y 是一个父节点则返回 false
                list.addAll(curVal);
            }
            if (list.contains(x) && list.contains(y))   return true;	//	如果在同一层则返回 true
            list.clear();
        }

        return false;
    }
}

腐烂的橘子

在给定的网格中，每个单元格可以有以下三个值之一：

值 0 代表空单元格；
值 1 代表新鲜橘子；
值 2 代表腐烂的橘子。
每分钟，任何与腐烂的橘子（在 4 个正方向上）相邻的新鲜橘子都会腐烂。

返回直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能，返回 -1。

示例一：

输入： [[2,1,1],[1,1,0],[0,1,1]]

输出： 4

示例二：

输入： [[2,1,1],[0,1,1],[1,0,1]]

输出： -1

解释： 左下角的橘子（第 2 行，第 0 列）永远不会腐烂，因为腐烂只会发生在 4 个正向上。

示例三：

输入： [[0,2]]

输出： 0

解释： 因为 0 分钟时已经没有新鲜橘子了，所以答案就是 0 。

AC代码：

class Solution {
    int[][] dir = {{-1, 0}, {0, -1}, {1, 0}, {0, 1}};
    public int orangesRotting(int[][] grid) {
        Queue<Integer> oranges = new LinkedList<>();
        Map<Integer, Integer> map = new HashMap<>();
        int R = grid.length, C = grid[0].length;
        for (int i = 0; i < R; i++)
            for (int j = 0; j < C; j++) {
                if (grid[i][j] == 2) {
                    oranges.offer(i * C + j);
                    map.put(i * C + j, 0);
                }
            }

        int ans = 0;
        while (!oranges.isEmpty()) {
            int size = oranges.size();
            for (int i = 0; i < size; i++) {
                int cur = oranges.poll();
                int curR = cur / C, curC = cur % C;
                for (int j = 0; j < dir.length; j++) {
                    int newR = curR + dir[j][0], newC = curC + dir[j][1];
                    if (newR >= 0 && newR < R && newC >= 0 && newC < C && grid[newR][newC] == 1) {
                        grid[newR][newC] = 2;
                        oranges.offer(newR * C + newC);
                        map.put(newR * C + newC, map.get(cur) + 1);
                        ans = map.get(newR * C + newC);
                    }
                }
            }
        }

        for (int i = 0; i < R; i++)
            for (int j = 0; j < C; j++)
                if (grid[i][j] == 1)    return -1;

        return ans;
    }
}

岛屿的最大面积

给定一个包含了一些 0 和 1 的非空二维数组 grid 。

一个岛屿是由一些相邻的 1 (代表土地) 构成的组合，这里的「相邻」要求两个 1 必须在水平或者竖直方向上相邻。你可以假设 grid 的四个边缘都被 0（代表水）包围着。

找到给定的二维数组中最大的岛屿面积。(如果没有岛屿，则返回面积为 0 。)

示例一：

输入：

[[0,0,1,0,0,0,0,1,0,0,0,0,0],
[0,0,0,0,0,0,0,1,1,1,0,0,0],
[0,1,1,0,1,0,0,0,0,0,0,0,0],
[0,1,0,0,1,1,0,0,1,0,1,0,0],
[0,1,0,0,1,1,0,0,1,1,1,0,0],
[0,0,0,0,0,0,0,0,0,0,1,0,0],
[0,0,0,0,0,0,0,1,1,1,0,0,0],
[0,0,0,0,0,0,0,1,1,0,0,0,0]]

输出： 6

示例二：

输入： [[0,0,0,0,0,0,0,0]]

输出： 0

AC代码：

class Solution {
    int[][] dir = {{1, 0}, {0, 1}, {-1, 0}, {0, -1}};
    public int maxAreaOfIsland(int[][] grid) {
        int row = grid.length, col = grid[0].length;
        if (row == 0 || col == 0)   return 0;
        
        int max_Island = 0;
        for (int i = 0; i < row; i++) {
            for (int j = 0; j < col; j++) {
                if (grid[i][j] == 1) {
                    int cur_Island = 0;
                    Queue<Integer> queue = new LinkedList<>();
                    queue.offer(i * col + j);
                    grid[i][j] = 0;
                    while (!queue.isEmpty()) {
                        int size = queue.size();
                        cur_Island += size;
                        for (int k = 0; k < size; k++) {
                            int cur = queue.poll();
                            int cur_Row = cur / col, cur_Col = cur % col;
                            for (int d = 0; d < 4; d++) {
                                int next_Row = cur_Row + dir[d][0], next_Col = cur_Col + dir[d][1];
                                if (next_Row >= 0 && next_Row < row && next_Col >= 0 && next_Col < col) {
                                    if (grid[next_Row][next_Col] == 1) {
                                        queue.offer(next_Row * col + next_Col);
                                        grid[next_Row][next_Col] = 0;
                                    }
                                } 
                            }
                        }
                    }
                    max_Island = Math.max(max_Island, cur_Island);
                }
            }
        }
        
        return max_Island;
    }
}

回溯算法

全排列

给定一个 没有重复 数字的序列，返回其所有可能的全排列。

示例一：

输入： [1,2,3]

输出：

[

[1,2,3],

[1,3,2],

[2,1,3],

[2,3,1],

[3,1,2],

[3,2,1]

]

回溯算法和DFS。

判断结束条件。
执行操作。
撤销之前的操作。

AC代码：

class Solution {
    List<List<Integer>> ans = new LinkedList<>();
    public List<List<Integer>> permute(int[] nums) {

        LinkedList<Integer> cur = new LinkedList<>();
        backtrack(nums, cur);

        return ans;
    }

    public void backtrack(int[] nums, LinkedList<Integer> cur) {
        if (cur.size() == nums.length) {
            ans.add(new LinkedList(cur));
            return;
        }

        for (int i = 0; i < nums.length; i++) {
            if (cur.contains(nums[i]))  continue;
            cur.add(nums[i]);
            backtrack(nums, cur);
            cur.removeLast();
        }
    }
}

class Solution {
    public List<List<Integer>> permute(int[] nums) {
        int len = nums.length;
        List<List<Integer>> res = new ArrayList<>();
        if (len == 0)   return res;

        Deque<Integer> path = new ArrayDeque<>();
        boolean[] used = new boolean[len];
        backTrack(nums, len, used, path, 0, res);

        return res;
    }
  	/**
  		nums	选择的范围
  		len		选择的范围的长度
  		used	记录访问过的数字
  		path	记录路径
  		depth	记录已经访问的路径深度
  		res		记录所有的排列组合
  	*/
    void backTrack(int[] nums, int len, boolean[] used, Deque<Integer> path, int depth, List<List<Integer>> res) {
      	//	先写结束条件
        if (depth == len) {
            res.add(new ArrayList(path));
            return;
        }

        for (int i = 0; i < len; i++) {
            if (used[i])    continue;

            path.addLast(nums[i]);
            used[i] = true;
            backTrack(nums, len, used, path, depth + 1, res);
            used[i] = false;	//	撤销前面执行的操作
            path.removeLast();
        }
    }
}

无重复字符串的排列组合

无重复字符串的排列组合。编写一种方法，计算某字符串的所有排列组合，字符串每个字符均不相同。

示例一：

输入： S = “qwe”

输出： [“qwe”, “qew”, “wqe”, “weq”, “ewq”, “eqw”]

示例二：

输入： S = “ab”

输出： [“ab”, “ba”]

提示:

字符都是英文字母。
字符串长度在[1, 9]之间。

回溯算法。和「全排列」一样的思想。

class Solution {
    public String[] permutation(String S) {
        int len = S.length();
        if (len == 0)   return new String[]{""};
        
      	//	保存结果的动态数组
        List<String> res = new ArrayList<>();
        boolean[] used =  new boolean[len];
        
        dfs(S, len, "", 0, used, res);

        String[] ans = new String[res.size()];
        for (int i = 0; i < res.size(); i++)
            ans[i] = res.get(i);

        return ans;
    }
  	/**
  		S			选择的范围
  		len		选择范围的长度
  		path	记录当前的排列组合
  		depth	记录组合了多少个字母
  		used	记录访问了哪些字母
  		res		记录所有排列组合
  	*/
    void dfs(String S, int len, String path, int depth, boolean[] used, List<String> res) {
        if (depth == len) {
            res.add(new String(path));	//	因为String是引用传递，所以这里需要new String()
            return;
        }

        for (int i = 0; i < len; i++) {
            if (used[i])    continue;

            String temp = new String(path);	//	保存这一步的path
            used[i] = true;
            path += S.charAt(i);
            dfs(S, len, path, depth + 1, used, res);
            used[i] = false;
            path = temp;
        }
    }
}

幂集

幂集。编写一种方法，返回某集合的所有子集。集合中不包含重复的元素。

示例一：

输入： nums = [1,2,3]

输出：

[

[3],

[1],

[2],

[2,1,3],

[1,3],

[2,3],

[1,2],

[]

]

说明：解集不能包含重复的子集。

回溯算法。巩固了一下回溯，这题和「全排列」的区别是：全排列有顺序之分，子集没有顺序之分。我们只要在稍微在 for 循环里改一下条件就可以了。

AC代码：

class Solution {
    public List<List<Integer>> subsets(int[] nums) {
        int len = nums.length;
        Deque<Integer> path = new ArrayDeque<>();
        List<List<Integer>> res = new ArrayList<>();
        boolean[] used = new boolean[len];

        for (int i = 1; i <= len; i++)
            dfs(nums, len, 0, 0, i, path, used, res);
        res.add(new ArrayList());	//	空集在最后单独加入
        return res;
    }
  	/**
  		nums	选择的范围
  		len		选择范围的长度
  		depth	当前选择了多少个数
  		cur		当前遍历到数组的位置
  		total	选择的子集包含多少个数
  		path	记录当前的子集
  		used	标记访问的数
  		res		记录所有子集
  	*/
    void dfs(int[] nums, int len, int depth, int cur, int total, Deque<Integer> path, boolean[] used, List<List<Integer>> res) {
        if (depth == total) {
            res.add(new ArrayList(path));
            return;
        }

      	//	循环在cur之后的数中进行选择
        for (int i = cur; i < len; i++) {
            if (used[i])    continue;

            used[i] = true;
            path.addLast(nums[i]);
            dfs(nums, len, depth + 1, i, total, path, used, res);
            path.removeLast();
            used[i] = false;
        }
    }
}

组合

给定两个整数 n 和 k，返回 1 … n 中所有可能的 k 个数的组合。

示例一：

输入： n = 4, k = 2

输出：

[

[2,4],

[3,4],

[2,3],

[1,2],

[1,3],

[1,4]

]

回溯算法。这题可以说是和「幂集」一样的。

class Solution {
    public List<List<Integer>> combine(int n, int k) {
        int[] nums = new int[n];
        for (int i = 0; i < n; i++)
            nums[i] = i + 1;

        boolean[] used = new boolean[n];
        List<List<Integer>> res = new ArrayList<>();
        Deque<Integer> path = new ArrayDeque<>();
        
        dfs(nums, 0, 0, k, path, used, res);
        
        return res;
    }
    void dfs(int[] nums, int cur, int depth, int total, Deque<Integer> path, boolean[] used, List<List<Integer>> res) {
        if (depth == total) {
            res.add(new ArrayList(path));
            return;
        }

        for (int i = cur; i < nums.length; i++) {
            if (used[i])    continue;

            used[i] = true;
            path.addLast(nums[i]);
            dfs(nums, i, depth + 1, total, path, used, res);
            used[i] = false;
            path.removeLast();
        }
    }
}

组合总和 III

找出所有相加之和为 n 的 k 个数的组合**。**组合中只允许含有 1 - 9 的正整数，并且每种组合中不存在重复的数字。

示例一：

输入： k = 3, n = 7

输出： [[1,2,3]]

示例二：

输入： k = 3, n = 9

输出： [[1,2,6], [1,3,5], [2,3,4]]

说明：

所有数字都是正整数。
解集不能包含重复的组合。

回溯算法。

class Solution {
    public List<List<Integer>> combinationSum3(int k, int n) {
        int len = 9;
        int[] nums = new int[len];
        for (int i = 0; i < len; i++)
            nums[i] = i + 1;
        
        List<List<Integer>> res = new ArrayList<>();
        Deque<Integer> path = new ArrayDeque<>();
        boolean[] used = new boolean[len];

        backTrack(nums, len, n, k, 0, 0, 0, used, path, res);

        return res;
    }
    void backTrack(int[] nums, int len, int n, int k, int depth, int cur, int sum, boolean[] used, Deque<Integer> path, List<List<Integer>> res) {
        if (depth == k) {
            if (sum == n)
                res.add(new ArrayList(path));
            return;
        }

        for (int i = cur; i < len; i++) {
            if (sum + nums[i] > n) break;	//	如果大于 n 就直接退出循环，不进行下面的逻辑
            if (used[i])    continue;

            sum += nums[i];
            used[i] = true;
            cur = i;
            path.addLast(nums[i]);
            backTrack(nums, len, n, k, depth + 1, cur, sum, used, path, res);
            sum -= nums[i];
            path.removeLast();
            used[i] = false;
        }
    }
}

分割的回文串

给定一个字符串 s，将 s 分割成一些子串，使每个子串都是回文串。

返回 s 所有可能的分割方案。

示例一：

输入： “aab”

输出：

[

[“aa”, “b”],

[“a”, “a”, “b”]

]

巩固一下回溯算法。

AC代码：

class Solution {
    List<List<String>> res = new ArrayList<>();
    public List<List<String>> partition(String s) {
        if (s.length() == 0)  return res;

        Deque<String> deque = new ArrayDeque<>();
        findStr(s, deque, 0);

        return res;
    }
    void findStr(String s, Deque<String> deque, int begin) {
        if (begin == s.length()) {
            res.add(new ArrayList(deque));
            return;
        }

        for (int i = begin; i < s.length(); i++) {
            if (isPalindrome(s, begin, i)) {
                deque.addLast(s.substring(begin, i + 1));
                findStr(s, deque, i + 1);
                deque.removeLast();
            }  
        }
    }
    boolean isPalindrome(String str, int begin, int end) {
        while (begin <= end) {
            if (str.charAt(begin) != str.charAt(end))   return false;
            begin++;
            end--;
        }

        return true;
    }
}

括号生成

数字 n 代表生成括号的对数，请你设计一个函数，用于能够生成所有可能的并且 有效的 括号组合。

示例一：

输入： 3

输出： [
“((()))”,
“(()())”,
“(())()”,
“()(())”,
“()()()”
]

AC代码：

class Solution {
    List<String> res = new ArrayList<>();
    public List<String> generateParenthesis(int n) {
        backTrack(n , "", 0, 0);

        return res;
    }
    void backTrack(int n, String path, int left, int right) {
        if (path.length() == 2 * n) {
            res.add(path);
            return;
        }

        if (left < n)   backTrack(n, path + "(", left + 1, right);
        if (right < left)   backTrack(n, path + ")", left, right + 1);
    }
}

电话号码的字母组合

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。

给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

示例一：

输入： “23”

输出： [“ad”, “ae”, “af”, “bd”, “be”, “bf”, “cd”, “ce”, “cf”]

说明:
尽管上面的答案是按字典序排列的，但是你可以任意选择答案输出的顺序。

AC代码：

class Solution {
    List<String> res = new ArrayList<>();
    String[] comb = {"abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
    public List<String> letterCombinations(String digits) {
        if (digits.length() == 0)    return res;
        
        backTrack(digits, "", 0);

        return res;
    }
    void backTrack(String S, String path, int index) {
        if (path.length() == S.length()) {
            res.add(path);
            return;
        }

        for (int j = 0; j < comb[S.charAt(index) - '0' - 2].length(); j++)
            backTrack(S, path + comb[S.charAt(index) - '0' - 2].charAt(j), index + 1);
    }
}

活字印刷

你有一套活字字模 tiles，其中每个字模上都刻有一个字母 tiles[i]。返回你可以印出的非空字母序列的数目。

**注意：**本题中，每个活字字模只能使用一次。

示例一：

输入： “AAB”

输出： 8

解释： 可能的序列为 “A”, “B”, “AA”, “AB”, “BA”, “AAB”, “ABA”, “BAA”。

示例二：

输入： “AAABBC”

输出： 188

用Set来存，避免重复。一开始用List存，添加的时候要判断，最后提交上去会爆掉。

AC代码

class Solution {
    Set<String> res = new HashSet<>();
    public int numTilePossibilities(String tiles) {
        int len = tiles.length();
        boolean[] used = new boolean[len];

        for (int i = 1; i <= len; i++)
            backTrack(tiles, len, 0, i, "", used);

        return res.size();
    }
    void backTrack(String tiles, int len, int depth, int total, String path, boolean[] used) {
        if (depth == total) {
            res.add(path);
            return;
        }

        for (int i = 0; i < len; i++) {
            if (used[i])    continue;

            used[i] = true;
            backTrack(tiles, len, depth + 1, total, path + tiles.charAt(i), used);
            used[i] = false;
        }
    }
}

长度为 n 的开心字符串中字典序第 k 小的字符串

一个「开心字符串」定义为：

仅包含小写字母 [‘a’, ‘b’, ‘c’].
对所有在 1 到 s.length - 1 之间的 i ，满足 s[i] != s[i + 1] （字符串的下标从 1 开始）。
比方说，字符串 “abc”，“ac”，“b” 和 “abcbabcbcb” 都是开心字符串，但是 “aa”，“baa” 和 “ababbc” 都不是开心字符串。

给你两个整数 n 和 k ，你需要将长度为 n 的所有开心字符串按字典序排序。

请你返回排序后的第 k 个开心字符串，如果长度为 n 的开心字符串少于 k 个，那么请你返回空字符串。

示例一：

输入： n = 1, k = 3

输出： “c”

解释： 列表 [“a”, “b”, “c”] 包含了所有长度为 1 的开心字符串。按照字典序排序后第三个字符串为 “c” 。

示例二：

输入： n = 1, k = 4

输出： “”

解释： 长度为 1 的开心字符串只有 3 个。

示例三：

输入： n = 3, k = 9

输出： “cab”

解释： 长度为 3 的开心字符串总共有 12 个 [“aba”, “abc”, “aca”, “acb”, “bab”, “bac”, “bca”, “bcb”, “cab”, “cac”, “cba”, “cbc”] 。第 9 个字符串为 “cab”

示例太多了就放三个。

AC代码：

class Solution {
    List<String> list = new ArrayList<>();
    String[] abc = {"a", "b", "c"};
    public String getHappyString(int n, int k) {
        for (int i = 0; i < 3; i++)
            backTrack(n, abc[i]);
        
        return k - 1 < list.size() ? list.get(k - 1) : "";
    }
    void backTrack(int n, String path) {
        if (path.length() == n) {
            System.out.println(path);
            list.add(path);
            return;
        }
        
        String cur = path.charAt(path.length() - 1) + "";
        if (!cur.equals(abc[0]))  backTrack(n, path + abc[0]);
        if (!cur.equals(abc[1]))  backTrack(n, path + abc[1]);
        if (!cur.equals(abc[2]))  backTrack(n, path + abc[2]);
    }
}

黄金矿工

你要开发一座金矿，地质勘测学家已经探明了这座金矿中的资源分布，并用大小为 m * n 的网格 grid 进行了标注。每个单元格中的整数就表示这一单元格中的黄金数量；如果该单元格是空的，那么就是 0。

为了使收益最大化，矿工需要按以下规则来开采黄金：

每当矿工进入一个单元，就会收集该单元格中的所有黄金。

矿工每次可以从当前位置向上下左右四个方向走。

每个单元格只能被开采（进入）一次。

不得开采（进入）黄金数目为 0 的单元格。

矿工可以从网格中 任意一个 有黄金的单元格出发或者是停止。

示例一：

输入： grid = [[0,6,0],[5,8,7],[0,9,0]]

输出： 24

解释：

[[0,6,0],
[5,8,7],
[0,9,0]]
一种收集最多黄金的路线是：9 -> 8 -> 7。

示例二：

输入： grid = [[1,0,7],[2,0,6],[3,4,5],[0,3,0],[9,0,20]]

输出： 28

解释：

[[1,0,7],
[2,0,6],
[3,4,5],
[0,3,0],
[9,0,20]]
一种收集最多黄金的路线是：1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 7。

AC代码：

class Solution {
    int[][] dir = {{1, 0}, {0, 1}, {-1, 0}, {0, -1}};
    boolean[][] visited = null;
    int row = 0, col = 0;
    int max_Gold = 0;
    public int getMaximumGold(int[][] grid) {
        row = grid.length;
        col = grid[0].length;
        visited = new boolean[row][col];
        
        for (int i = 0; i < row; i++)
            for (int j = 0; j < col; j++)
                if (grid[i][j] != 0) {
                    visited[i][j] = true;
                    backTrack(grid, visited, i, j, grid[i][j]);
                    visited[i][j] = false;
                }
        
        return max_Gold;
    }
    void backTrack(int[][] grid, boolean[][] visited, int cur_Row, int cur_Col, int cur_Gold) {
        max_Gold = Math.max(max_Gold, cur_Gold);
        for (int i = 0; i < 4; i++) {
            int new_Row = cur_Row + dir[i][0], new_Col = cur_Col + dir[i][1];
            if (new_Row >= 0 && new_Row < row && new_Col >= 0 && new_Col < col) {
                if (visited[new_Row][new_Col] || grid[new_Row][new_Col] == 0) continue;	//	不能用 return 
                
                visited[new_Row][new_Col] = true;
                backTrack(grid, visited, new_Row, new_Col, cur_Gold + grid[new_Row][new_Col]);
                visited[new_Row][new_Col] = false;
            }
        }
    }
}

贪心算法

用户分组

有 n 位用户参加活动，他们的 ID 从 0 到n - 1，每位用户都恰好属于某一用户组。给你一个长度为 n 的数组groupSizes，其中包含每位用户所处的用户组的大小，请你返回用户分组情况（存在的用户组以及每个组中用户的 ID）。

你可以任何顺序返回解决方案，ID 的顺序也不受限制。此外，题目给出的数据保证至少存在一种解决方案。

示例一：

输入： groupSizes = [3,3,3,3,3,1,3]

输出： [[5],[0,1,2],[3,4,6]]

解释：

其他可能的解决方案有 [[2,1,6],[5],[0,4,3]] 和 [[5],[0,6,2],[4,3,1]]。

示例二：

输入： groupSizes = [2,1,3,3,3,2]

输出： [[1],[0,5],[2,3,4]]

看题看了半天。贪心，满足条件就加入。

AC代码：

class Solution {
    public List<List<Integer>> groupThePeople(int[] groupSizes) {
        List<List<Integer>> res = new ArrayList<>();
        boolean[] visited = new boolean[groupSizes.length];	//	标记访问过的ID

        for (int i = 0; i < groupSizes.length; i++) {
            if (visited[i]) continue;
            List<Integer> cur = new ArrayList<>();
            int cnt = 0;	//	记录添加的ID数目
            for (int j = 0; j < groupSizes.length && cnt < groupSizes[i]; j++) {
                if (visited[j]) continue;
                if (groupSizes[i] == groupSizes[j]) {
                    cur.add(j);
                    visited[j] = true;
                    cnt++;
                }
            }
            res.add(cur);
        }

        return res;
    }
}

跳跃游戏 II

给定一个非负整数数组，你最初位于数组的第一个位置。

数组中的每个元素代表你在该位置可以跳跃的最大长度。

你的目标是使用最少的跳跃次数到达数组的最后一个位置。

示例一：

输入： [2,3,1,1,4]

输出： 2

解释： 跳到最后一个位置的最小跳跃数是 2。
从下标为 0 跳到下标为 1 的位置，跳 1 步，然后跳 3 步到达数组的最后一个位置。

从后向前贪心。

AC代码：

class Solution {
    public int jump(int[] nums) {
        int res = 0, index = nums.length - 1;
        while (index > 0) {
            for (int i = 0; i < nums.length; i++)
                if (i + nums[i] >= index) {
                    index = i;
                    res++;
                    break;
                }
        }
        
        return res;
    }
}

动态规划

最大正方形

在一个由 0 和 1 组成的二维矩阵内，找到只包含 1 的最大正方形，并返回其面积。

示例一：

输入：

1 0 1 0 0
1 0 1 1 1
1 1 1 1 1
1 0 0 1 0

输出： 4

AC代码：

class Solution {
    public int maximalSquare(char[][] matrix) {
        if (matrix.length == 0 || matrix[0].length == 0)    return 0;

        int row = matrix.length, col = matrix[0].length;
        int maxSize = 0;
        int[][] dp = new int[row][col];
        for (int i = 0; i < row; i++) {
            for (int j = 0; j < col; j++) {
                if (matrix[i][j] == '1') {
                    if (i == 0 || j == 0)   dp[i][j] = 1;
                    else {
                        dp[i][j] = Math.min(dp[i - 1][j - 1], Math.min(dp[i - 1][j], dp[i][j - 1])) + 1;
                    }
                    maxSize = Math.max(maxSize, dp[i][j]);
                }
            }
        }

        return maxSize * maxSize;
    }
}

统计全为 1 的正方形子矩阵

给你一个 m * n 的矩阵，矩阵中的元素不是 0 就是 1，请你统计并返回其中完全由 1 组成的 正方形 子矩阵的个数。

示例一：

输入： matrix =

[
[0,1,1,1],
[1,1,1,1],
[0,1,1,1]
]

输出： 15

解释：

边长为 1 的正方形有 10 个。
边长为 2 的正方形有 4 个。
边长为 3 的正方形有 1 个。
正方形的总数 = 10 + 4 + 1 = 15.

示例二：

输入： matrix =

[
[1,0,1],
[1,1,0],
[1,1,0]
]

输出： 7

解释：

边长为 1 的正方形有 6 个。
边长为 2 的正方形有 1 个。
正方形的总数 = 6 + 1 = 7.

AC代码：

class Solution {
    public int countSquares(int[][] matrix) {
        int row = matrix.length, col = matrix[0].length;
        int[][] dp = new int[row][col];
        int res = 0;
        
        for (int i = 0; i < row; i++) {
            for (int j = 0; j < col; j++) {
                if (matrix[i][j] == 1) {
                    if (i == 0 || j == 0)   dp[i][j] = 1;
                    else    
                        dp[i][j] = Math.min(dp[i - 1][j - 1], Math.min(dp[i - 1][j], dp[i][j - 1])) + 1;
                    res += dp[i][j];
                }
            }
        }

        return res;
    }
}

礼物的最大价值

在一个 m*n 的棋盘的每一格都放有一个礼物，每个礼物都有一定的价值（价值大于 0）。你可以从棋盘的左上角开始拿格子里的礼物，并每次向右或者向下移动一格、直到到达棋盘的右下角。给定一个棋盘及其上面的礼物的价值，请计算你最多能拿到多少价值的礼物？

示例一：

输入：

[
[1,3,1],
[1,5,1],
[4,2,1]
]

输出： 12

解释： 路径 1 -> 3 ->5 -> 2 -> 1 可以拿到最多价值的礼物

动态规划。对于任意的 grid[i][j] ，

当 i != 0 && j != 0 时，grid[i][j] = Math.max(grid[i - 1][j], grid[i][j - 1])。

当 i = 0 时，grid[0][j] += grid[0][j - 1]。

当 j = 0 时，grid[i][0] += grid[i - 1][0]。

AC代码：

class Solution {
    public int maxValue(int[][] grid) {
        if (grid.length == 0 || grid[0].length == 0)    return 0;

        int row = grid.length, col = grid[0].length;
        for (int i = 1; i < row; i++)	//	处理第一列
            grid[i][0] += grid[i - 1][0];
        for (int i = 1; i < col; i++)	//	处理第一行
            grid[0][i] += grid[0][i - 1];
        for (int i = 1; i < row; i++)
            for (int j = 1; j < col; j++)
                grid[i][j] += Math.max(grid[i - 1][j], grid[i][j - 1]);

        return grid[row - 1][col - 1];
    }
}

股票的最大利润

假设把某股票的价格按照时间先后顺序存储在数组中，请问买卖该股票一次可能获得的最大利润是多少？

示例一：

输入： [7,1,5,3,6,4]

输出： 5

解释： 在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6 - 1 = 5

示例二：

输入： [7,6,4,3,1]

输出： 0

AC代码：

class Solution {
    public int maxProfit(int[] prices) {
        int buy = Integer.MAX_VALUE, profit = 0;
        for (int cur: prices) {
            buy = Math.min(cur, buy);
            profit = Math.max(profit, cur - buy);
        }

        return profit;
    }
}

最小路径和

给定一个包含非负整数的 m x n 网格，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

**说明：**每次只能向下或者向右移动一步。

示例一：

输入：

[
[1,3,1],
[1,5,1],
[4,2,1]
]

输出： 7

解释： 因为路径 1 -> 3 -> 1 -> 1 -> 1 的总和最小。

动态规划。dp[i][j] 储存走到当前位置的最短路径和。

AC代码：

class Solution {
    public int minPathSum(int[][] grid) {
        int row = grid.length, col = grid[0].length;
        if (row == 0 || col == 0)   return 0;

        int[][] dp = new int[row][col];
        dp[0][0] = grid[0][0];
        for (int i = 1; i < row; i++)
            dp[i][0] = dp[i - 1][0] + grid[i][0];
        for (int i = 1; i < col; i++)
            dp[0][i] = dp[0][i - 1] + grid[0][i];

        for (int i = 1; i < row; i++) {
            for (int j = 1; j < col; j++) {
                dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];
            }
        }

        return dp[row - 1][col - 1];
    }
}

不同路径 II

一个机器人位于一个 m x n 网格的左上角（起始点在下图中标记为“Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。

现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？

网格中的障碍物和空位置分别用 1 和 0 来表示。

示例一：

输入：

[
[0,0,0],
[0,1,0],
[0,0,0]
]

输出： 2

解释：

3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径：

向右 -> 向右 -> 向下 -> 向下

向下 -> 向下 -> 向右 -> 向右

AC代码：

class Solution {
    public int uniquePathsWithObstacles(int[][] grid) {
        int row = grid.length, col = grid[0].length;
        if (row == 0 || col == 0)   return 0;
        if (grid[0][0] == 1 || grid[row - 1][col - 1] == 1)    return 0;
        
        grid[0][0] = 1;
        for (int i = 1; i < row; i++)
            grid[i][0] = (grid[i][0] == 0 && grid[i - 1][0] == 1) ? 1 : 0;
        for (int i = 1; i < col; i++)
            grid[0][i] = (grid[0][i] == 0 && grid[0][i - 1] == 1) ? 1 : 0;
        
        
        // for (int i = 0; i < row; i++)
        //     for (int j = 0; j < col; j++)
        //         if (grid[i][j] == 1)    grid[i][j] = -1;
        
        for (int i = 1; i < row; i++) {
            for (int j = 1; j < col; j++) {
                if (grid[i][j] == 1)    grid[i][j] = 0;
                else    grid[i][j] = grid[i - 1][j] + grid[i][j - 1];
            }
        }
        
        return grid[row - 1][col - 1];
    }
}

爬楼梯

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

**注意：**给定 n 是一个正整数。

示例一：

输入： 2

输出： 2

解释： 有两种方法可以爬到楼顶。

1 阶 + 1 阶

2 阶

示例二：

输入： 3

输出： 3

解释： 有三种方法可以爬到楼顶。

1 阶 + 1 阶 + 1 阶

1 阶 + 2 阶

2 阶 + 1 阶

AC代码：

class Solution {
    public int climbStairs(int n) {
        if (n == 1) return 1;
        if (n == 2) return 2;
        int[] dp = new int[n + 1];
        dp[1] = 1;
        dp[2] = 2;
        
        for (int i = 3; i <= n; i++)
            dp[i] = dp[i - 1] + dp[i - 2];
        
        return dp[n];
    }
}

和为 K 的子数组

给定一个整数数组和一个整数 **k，**你需要找到该数组中和为 k 的连续的子数组的个数。

示例一：

输入： nums = [1,1,1], k = 2

输出： 2 , [1,1] 与 [1,1] 为两种不同的情况。

说明：

数组的长度为 [1, 20,000]。
数组中元素的范围是 [-1000, 1000] ，且整数 k 的范围是 [-1e7, 1e7]。

两种方法：
1. **计算前缀和。**再遍历数组
2. 用Map储存。

AC代码：

//	计算前缀和
class Solution {
    public int subarraySum(int[] nums, int k) {
        if (nums.length == 0)   return 0;
        
        int res = 0, n = nums.length;
        int[] dp = new int[n + 1];
        for (int i = 0; i < n; i++)
            dp[i + 1] = dp[i] + nums[i];
        
        for (int i = 0; i < n + 1; i++)
            for (int j = i + 1; j < n + 1; j++)
                if (dp[j] - dp[i] == k) res++;
        
        return res;
    }
}

//	Map
class Solution {
    public int subarraySum(int[] nums, int k) {
        int res = 0, pre = 0;
        Map<Integer, Integer> map = new HashMap<>();
        map.put(0, 1);
        
        for (int i = 0; i < nums.length; i++) {
            pre += nums[i];
            if (map.containsKey(pre - k))   res += map.get(pre - k);
            map.put(pre, map.getOrDefault(pre, 0) + 1);
        }
        
        return res;
    }
}

结尾

发现在Typora上写完然后导入到CSDN会有兼容性问题，今天有空改了下小问题。

LeetCode 刷题题目总结

文章目录

前言

LeetCode 总结

整数反转

字符串中的第一个唯一字符

有效的字母异位词

字符串转换整数

实现 strStr()

跳跃游戏

盛最多水的容器

统计「优美子数组」

在排序数组中查找元素的第一个和最后一个位置

搜索二维矩阵

相对名次

旅行终点站

保护城市天际线

砖墙

二叉树的最近公共祖先

顺次数

链表

删除链表中的节点

环形链表

回文链表

合并两个有序链表

滑动窗口

无重复字符的最长子串

BFS & DFS

岛屿数量

二叉树的右视图

找树左下角的值

从上到下打印二叉树 II

N叉树的最大深度

N叉树的层序遍历

从上到下打印二叉树

特定深度节点链表

跳跃游戏 III

二叉树的最小深度

对称的二叉树

二叉树的堂兄弟节点

腐烂的橘子

岛屿的最大面积

回溯算法

全排列

无重复字符串的排列组合

幂集

组合

组合总和 III

分割的回文串

括号生成

电话号码的字母组合

活字印刷

长度为 n 的开心字符串中字典序第 k 小的字符串

黄金矿工

贪心算法

用户分组

跳跃游戏 II

动态规划

最大正方形

统计全为 1 的正方形子矩阵

礼物的最大价值

股票的最大利润

最小路径和

不同路径 II

爬楼梯

和为 K 的子数组

结尾

你可能感兴趣的:(LeetCode 刷题题目总结)