数值分析实验报告 Lab2 埃尔米特（Hermite）插值

数值分析实验报告 Lab2 埃尔米特（Hermite）插值

一、问题引出

1. 掌握埃尔米特插值算法原理；
2. 使用C语言编程实现埃尔米特插值算法。

二、实验准备

• 阅读《数值分析》——李庆阳 2.4节

三、实验要求

问题： 某人从甲地开车去乙地，每隔一段时间对行车距离和速率进行一次采样，得到在 $n+1$ 个采样时刻点 $t_i$ 的里程 $s_i$ 和速率 $v_i（i=0,1,...,n）$。要求编程构造埃尔米特插值多项式 $H_{2n+1}(t)$，满足 $H_{2n+1}(t_i)=s_i$，$H_{2n+1}^{\prime }(t_i)=v_i$，对所有 $i=0,1,...,n$ 成立，并据此计算 $m$ 个给定时刻的里程和速率。

函数接口定义：

void Hermite_Interpolation( int N, double t[], double s[], double v[], int m, double ht[], double hs[], double hv[] );

其中 $N$ 为采样点个数（注意这个 N 不是公式中的最大下标 n，而是等于 n+1），采样时刻点 $t_i$、里程 $s_i$、速率 $v_i$ 分别通过 $t、s、v$ 传入；$m$ 是需要估算的给定时刻的个数，$ht$ 传入给定的时刻点，相应计算出的里程和速率应分别存储在 $hs$ 和 $hv$ 中。

裁判程序如下：

#include

#define MAXN 5 /* 最大采样点个数 */
#define MAXM 10 /* 最大估算点个数 */

void Hermite_Interpolation( int N, double t[], double s[], double v[], int m, double ht[], double hs[], double hv[] );

int main()
{
  int N; /*确定给定的N=n+1组数据*/
  double t[MAXN], s[MAXN], v[MAXN]; /* 用于构造的数据 */
  double ht[MAXM], hs[MAXM], hv[MAXM]; /* 用估算的数据 */

  int m; //我们要估算的数据组数
  int i; //类似指向
  
 //
 //可以说是主要部分了
  while ( scanf("%d", &N) != EOF ) {
  
 //第一部分 
 //输入数据，可以说用于插值-构造Hermite插值多项式了
    for ( i=0; i<N; i++ ){scanf("%lf", &t[i]);}
    for ( i=0; i<N; i++ ){scanf("%lf", &s[i]);}
    for ( i=0; i<N; i++ ){scanf("%lf", &v[i]);}   
  //小停一会，这里我们输入的是要测算的组数与数据
    //组数
    scanf("%d", &m);
    //时间
    for ( i=0; i<m; i++ ){scanf("%lf", &ht[i]);}

  //空一行，为了美观
    printf("\n");
      
  //第二部分    
  //调用函数
    Hermite_Interpolation( N, t, s, v, m, ht, hs, hv );
    
  //第三部分  
  //输出数据
    //速度
    for ( i=0; i<m; i++ ){printf("%.4lf ", hs[i]);} /*小数点4位，双精度double类型*/
    printf("\n");/*空行鸭*/
    //里程
    for ( i=0; i<m; i++ ){printf("%.4lf ", hv[i]);}
    printf("\n\n");/*空行鸭*/
    
  }
  return 0;
}

裁判输入数据：

2
0.0 1.0
0.0 1.0
0.0 0.0
5
0.0 0.2 0.5 0.8 1.0

3
0.0 0.5 1.0
100.0 170.0 200.0
30.0 150.0 0.0
5
0.0 0.25 0.5 0.75 1.0

5
0.0 1.0 2.0 3.0 4.0
0.0 60.0 160.0 260.0 300.0
5.0 70.0 100.0 120.0 20.0
10
0.5 1.0 1.5 2.0 2.5 3.0 3.5 3.8 3.95 4.0

标准输出数据：

0.0000 0.1040 0.5000 0.8960 1.0000
0.0000 0.9600 1.5000 0.9600 0.0000
`100.0000 127.9297 170.0000 195.9766 200.0000 ` `30.0000 165.4688 150.0000 52.9688 0.0000 `
30.2222 60.0000 105.9303 160.0000 206.3438 260.0000 307.9764 305.7687 299.9796 300.0000
62.6024 70.0000 109.0488 100.0000 92.9745 120.0000 41.2374 -44.8421 -16.2783 20.0000

四、原理分析

(一) 什么是Hermite插值

• 我们需要研究两点三次Hermite插值，因为与本题类似。

---

(二) 简单模型，两点三次Hermite插值

---

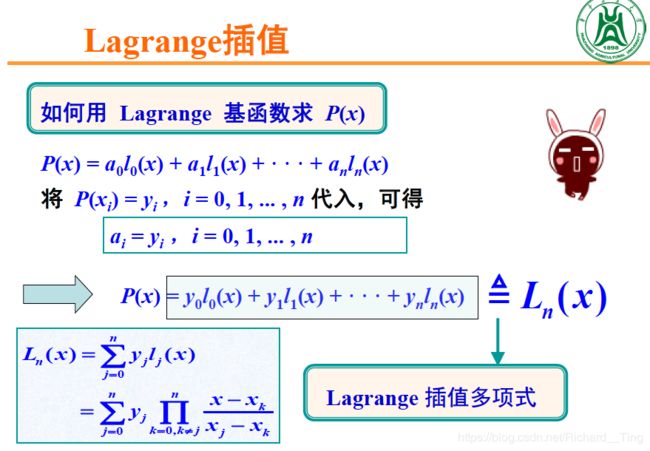
讲解Lagrange插值原理

---

回到两点三次Hermite插值

• 值得一说的是，下面式子给出 $H^{\prime }(x)$ 和 $H(x)$ 时会更好些。
  

说完了上述的两点三次Hermite插值，下面就可以延拓为本题的问题了。

---

(三) 真正的挑战，多点多次Hermite插值

因为 $h_i(x)$ 和 $h_i^{\prime }(x)$ 都为0，故为2重根。

五、代码总结

//
//  main.cpp
//  Hermite
//
//  Created by apple on 2018/10/16.
//  Copyright © 2018年 apple. All rights reserved.

#include

#define MAXN 5 /* 最大采样点个数 */
#define MAXM 10 /* 最大估算点个数 */

//函数声明与函数定义
void Hermite_Interpolation( int N, double t[], double s[], double v[], int m, double ht[], double hs[], double hv[] )
{
    //腾出空间，加快运行速度
    double l[10],p[10],h1[10],h2[10],x,ll[10],pp[10];
    
    /*l->l_i(x)*/
    /*h1->h_i(x)*/
    /*h2->h'_i(x)*/
    /*x类似于替换缓存数据*/
    /*pp->l'_i(x)*/
    
    int kk;//下标作用
    for(kk=0;kk<m;kk++)//逐个预测m+1个数据
    {
        x=ht[kk];hs[kk]=0;hv[kk]=0;//需要判断某时刻我们需要估算的速度与里程
        
        int i;//下标作用，n+1个数据迭代
        for(i=0;i<N;i++)
        {
            //######################################
            l[i]=1;ll[i]=1;
            //更新l_i(x)
            int j;//下标作用
            for(j=0;j<N;j++)
            {
                if(i!=j)
                {
                    l[i]=l[i]*(x-t[j])/(t[i]-t[j]);
                }
            }
            //######################################
            p[i]=0;pp[i]=0;
            //更新l'_i(x)
            int k;//下标作用
            for(k=0;k<N;k++)
            {
                if(i!=k)
                {
                    p[i]=p[i]+l[i]/(x-t[k]);
                    pp[i]=pp[i]+ll[i]/(t[i]-t[k]);
                }
            }
            //######################################
            /*公式部分*/
            //h_i(x)
            h1[i]=(1-2*pp[i]*(x-t[i]))*l[i]*l[i];
            //h'_i(x)
            h2[i]=(x-t[i])*l[i]*l[i];
            //Hermite插值公式
            hs[kk]=hs[kk]+s[i]*h1[i]+v[i]*h2[i];
            //######################################
            /*预测数据部分*/
            
            int kkk;//下标作用
            for(kkk=0;kkk<N;kkk++)
            {
            //若需判断的时刻是我们之前已知的时刻，跳出
                if(x==t[kkk])
                    break;
                
            }
            //若需判断的时刻是我们之前已知的时刻，速度相同
            if(x==t[kkk])
                hv[kk]=v[kkk];
            //否则，速度作出调整,速度是由里程求导而来的
            else
                hv[kk]=hv[kk]+s[i]*(2*p[i]*l[i]-4*l[i]*p[i]*(x-t[i])*pp[i]-2*pp[i]*l[i]*l[i])+v[i]*(l[i]*l[i]+2*l[i]*p[i]*(x-t[i]));
            
        }
    }
}

//主函数
int main()
{
  int N; /*确定给定的N=n+1组数据*/
  double t[MAXN], s[MAXN], v[MAXN]; /* 用于构造的数据 */
  double ht[MAXM], hs[MAXM], hv[MAXM]; /* 用估算的数据 */

  int m; //我们要估算的数据组数
  int i; //类似指向

 //可以说是主要部分了
  while ( scanf("%d", &N) != EOF ) {
  
 //输入数据，可以说用于插值-构造Hermite插值多项式了
    for ( i=0; i<N; i++ ){scanf("%lf", &t[i]);}
    for ( i=0; i<N; i++ ){scanf("%lf", &s[i]);}
    for ( i=0; i<N; i++ ){scanf("%lf", &v[i]);}
      
  //小停一会，这里我们输入的是要测算的组数与数据
    //组数
    scanf("%d", &m);
    //时刻
    for ( i=0; i<m; i++ ){scanf("%lf", &ht[i]);}
      
  //调用函数
    Hermite_Interpolation( N, t, s, v, m, ht, hs, hv );
    
  //输出答案鸭
    //里程
    for ( i=0; i<m; i++ ){printf("%.4lf ", hs[i]);}
    printf("\n");/*空行鸭*/
    //速度
    for ( i=0; i<m; i++ ){printf("%.4lf ", hv[i]);}
    printf("\n\n");/*空行鸭*/
    
  }
  return 0;
}

• 部分结果显示
  
  

---

@author Richard_vim
@E-mail: [email protected]
@date 10.16
@date 11.05 modified