Deep Clustering with Convolutional Autoencoders
International Conference on Neural Information Processing - 2017
Code:https://github.com/XifengGuo/DCEC
1 Introduction
给定无标注图像,如何将其分成K个潜在的空间?传统算法:1)首先根据领域特定的知识提取feature vectors 2)对提取出的feature vectors应用聚类算法。然而深度学习方法的出现,一些工作成功地将feature learning和clustering组合成为一个统一的框架,它可以直接在原始图像上进行聚类,表现得甚至更好。我们称这种形式的聚类算法为Deep Clustering。
深度聚类的关键因素是什么还尚不明确。例如:哪种神经网络用于提取特征是正确的?如何提供指导信息?i.e.定义clustering oriented loss function?数据的那些属性应该在特征空间中被保留?本文中我们关注的是第一点和第三点,得出总结:Convolutional AutoEncoders (CAE)和局部特征是深度聚类算法的两个关键因素。
Stacked AutoEncoders (SAE)在以end-to-end训练前需要layer-wise的预训练,网络层数加深时,预训练步骤会变得十分耗时。而且SAE用的是全连接层,处理图像时十分低效。[7]是第一个尝试不使用预训练直接以end-to-end方式训练CAE的。
Deep Embedded Clustering (DEC) [15]以self-learning的方式定义了有效的objective。定义的聚类损失可以同时更新转换网络和聚类中心参数的更新。但是他们忽略了数据属性的preservation,这可能导致特征空间的corruption。
We improve DEC algorithm by preserving local structure of data generating distribution and by incorporating convolutional layers.
We propose the Deep Convolutional Embedded Clustering (DCEC) algorithm to automatically cluster images. The DCEC takes advantages of CAE and local structure preservation. And the resulting optimization problem can be efficiently solved by mini-batch stochastic gradient descent and backpropagation.
2 Convolutional AutoEncoders
全连接自编码器:
f w ( x ) = σ ( W x ) ≡ h f_w(x)=\sigma(Wx)\equiv h fw(x)=σ(Wx)≡h g u ( h ) = σ ( U h ) g_u(h)=\sigma(Uh) gu(h)=σ(Uh)
卷积自编码器是将乘改为卷积的形式。
我们提出了一个新的CAE,无需冗余的layer-wise预训练,如图1所示。首先,一些卷积层堆叠起来用于提取特征,然后在最后一个卷积层flatten形成一个vector,其后是一个10units的全连接层,它被称为embedded layer。输入的2D图像因此被转换到了10D的特征空间中。为了以无监督的形式训练它,我们使用一个全连接层和一些卷积转之层来讲embedded feature转回初始的图像。encoder: h = F w ( x ) h=F_w(x) h=Fw(x) ,decoder: x ′ = G w ′ ( h ) x'=G_{w'}(h) x′=Gw′(h)的参数用最小化重构误差来更新: L r = 1 n Σ i = 1 n ∣ ∣ G w ′ ( F w ( x i ) ) − x i ∣ ∣ 2 2 L_r=\frac{1}{n}\Sigma_{i=1}^{n}||G_{w'}(F_w(x_i))-x_i||_2^2 Lr=n1Σi=1n∣∣Gw′(Fw(xi))−xi∣∣22
其中n是数据集中图像的数量, x i ∈ R 2 x_i\in R^2 xi∈R2表示第i个图像。

我们提出的CAE的关键因子是施加在embedded layer上的aggressive constraint。如果嵌入层足够大,网络应该可以复制它的输入到输出,这导致了学到无用的特征。直觉上避免恒等映射是为了控制潜在编码h的维度低于输入数据x。学习这样的under-comlete representations迫使自编码器步骤数据最重要的特征。因此我们迫使嵌入空间的维度与数据集的聚类数相等。In this way,网络可以直接以end-to-end训练,无需Dropout或BN之类的正则化。(Why?)
另一个因子是我们用带步长的卷积层代替encoder中的池化层,decoder中用带步长的转置卷积层。因为卷积(转置)可以是网络学到特殊的下采样(上采样),会得到更好的转换能力。
3 Deep Convolutional Embedded Clustering
我们使用CAE代替SAE拓展了DEC。我们认为仅仅使用clustering oriented loss会使嵌入特征空间被distorted。因此自编码器的重构损失也被加入到损失函数中,与聚类损失同时被优化。自编码器会保留生成的数据分布的局部结构,避免了特征空间的干扰。最终算法就是DCEC。下面我们首先介绍DCEC的网络结构,然后介绍clustering loss and local structure preservation mechanism ,最后提出优化步骤。
3.1 Structure of Deep Convolutional Embedded Clustering

DCEC由CAE(图1)和一个连接到CAE嵌入层的聚类层组成,如图2.聚类层将每个输入图像 x i x_i xi的嵌入点 z i z_i zi映射到一个soft label上。然后聚类损失 L c L_c Lc被定义为soft labels的分布与预先定义的目标分布之间的KL散度。CAE用于学习嵌入特征,聚类损失指导特征更易于形成聚类。
DCEC的目标函数是 L = L r + γ L c L=L_r+\gamma L_c L=Lr+γLc其中 L r L_r Lr和 L c L_c Lc是重构损失和聚类损失, γ > 0 \gamma>0 γ>0用于控制distorting嵌入层的程度。当 γ = 1 , L r ≡ 0 \gamma=1,L_r\equiv0 γ=1,Lr≡0,就变成了DEC[15]的损失函数。
3.2 Clustering Layer and Clustering Loss
聚类层和损失直接从DEC[15]借用。简要复习一下以完善DCEC结构。
聚类层将聚类中心 { μ j } 1 K \{{\mu_j}\}_1^K {μj}1K作为可训练的权重,通过Student’s t-distribution[8]将每个嵌入点 z i z_i zi映射到soft label q i q_i qi: q i j = ( 1 + ∣ ∣ z i − μ j ∣ ∣ 2 ) − 1 Σ j ( 1 + ∣ ∣ z i − μ j ∣ ∣ 2 ) − 1 ( 6 ) q_{ij}=\frac{(1+||z_i-\mu_j||^2)^{-1}}{\Sigma_j(1+||z_i-\mu_j||^2)^{-1}}(6) qij=Σj(1+∣∣zi−μj∣∣2)−1(1+∣∣zi−μj∣∣2)−1(6)其中 q i j q_{ij} qij是 q i q_i qi的第j个元素,表示 z i z_i zi属于类j的概率。
聚类损失被定义为
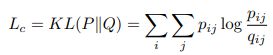
P是目标分布,定义为

3.3 Reconstruction Loss for Local Structure Preservation
DEC[15]抛弃了decoder使用聚类损失 L c L_c Lc微调encoder。然而我们认为这种微调会distort嵌入空间,弱化嵌入空间的表示能力进而影响聚类表现。[12]和[3]表明自编码器可以保留数据生成分布的局部结构。
3.4 Optimization
我们首先将 γ \gamma γ设为0来预训练CAE,得到有意义的目标分布。预训练之后,聚类中心通过在所有图像的嵌入特征上执行k-means来初始化。然后将 γ \gamma γ设为0.1更新CAE的权重,其后更新聚类中心和目标分布P。
Update autoencoders’ weights and cluster centers. 因为 ∂ L c ∂ z i \frac{\partial L_c}{\partial z_i} ∂zi∂Lc和 ∂ L c ∂ μ j \frac{\partial L_c}{\partial \mu_j} ∂μj∂Lc容易求偏导得到[15],权重和中心就可以直接用mini-batch SGD和反向传播更新。
Update target distribution. 目标分布P用于soft label的ground truth但是又依赖于预测的soft label。因此,为了避免不稳定,P不应该每次计算完一个batch的数据后就立即更新。实际上,我们每T次迭代后使用所有的嵌入点更新一次目标分布。(6)和(8)是更新公式。
训练过程的终止条件:两个连续的更新中目标分布的label assignments变化小于某个阈值 δ \delta δ。
4 Experiment
The proposed DCEC method is evaluated on three image datasets: MNISTfull: The MNIST dataset [6] consists of total 70000 handwritten digits of 28x28pixels. MNIST-test: The test set of MNIST, containing 10000 images. USPS:The USPS dataset contains 9298 gray-scale handwritten digit images with size
of 16x16 pixels.
Sumary 总体流程
需要更新的参数:网络的权重,聚类中心,目标分布
MNIST数据集
- 预训练不含聚类loss的CAE网络,每个输入会得到一个10D的embedding z i z_i zi
- 对所有 z i z_i zi应用k-means得到10个初始化聚类中心 μ j \mu_j μj,有了 μ j \mu_j μj和 z i z_i zi就可以根据公式 q i j = ( 1 + ∣ ∣ z i − μ j ∣ ∣ 2 ) − 1 Σ j ( 1 + ∣ ∣ z i − μ j ∣ ∣ 2 ) − 1 q_{ij}=\frac{(1+||z_i-\mu_j||^2)^{-1}}{\Sigma_j(1+||z_i-\mu_j||^2)^{-1}} qij=Σj(1+∣∣zi−μj∣∣2)−1(1+∣∣zi−μj∣∣2)−1计算得到 q i j q_{ij} qij,然后就可以计算出用作聚类损失的ground truth的真实分布 p i j p_{ij} pij, p i j = q i j 2 / Σ i q i j Σ i ( q i j 2 / Σ i q i j ) p_{ij}=\frac{q_{ij}^2/\Sigma_iq_{ij}}{\Sigma_i(q_{ij}^2/\Sigma_iq_{ij})} pij=Σi(qij2/Σiqij)qij2/Σiqij聚类损失公式: L c = K L ( P ∣ ∣ Q ) = Σ i Σ j p i j l o g p i j q i j L_c=KL(P||Q)=\Sigma_i\Sigma_jp_{ij}log\frac{p_{ij}}{q_{ij}} Lc=KL(P∣∣Q)=ΣiΣjpijlogqijpij
- 将 γ \gamma γ设为0.1开始训练重构损失和聚类损失,网络权重可以通过BP更新,聚类中心也可以: ∂ L c ∂ μ j = ∂ L c ∂ q ∂ q ∂ μ \frac{\partial L_c}{\partial \mu_j}=\frac{\partial L_c}{\partial q}\frac{\partial q}{\partial \mu} ∂μj∂Lc=∂q∂Lc∂μ∂q
- 为了保证稳定性,不能每个batch就更新一次作为GT的P,而是每T次迭代后使用所有样本的 z i z_i zi更新一次。
终止条件:两次更新目标分布P的变化小于某个阈值 δ \delta δ