机器学习笔记——5 生成学习算法(线性判别法LDA、二次判别法QDA及朴素贝叶斯NB算法的数学原理及其python实现)

生成学习算法(高斯判别和朴素贝叶斯算法的数学原理及其python实现)

本篇介绍另外一种分类算法，这类算法跟之前广义线性模型下的各种分类特例，比如logit分类、softmax分类等，在基本思想有根本的不同，这类算法称为生成学习算法。
本篇将首先介绍生成学习算法的基本思想，以此为基础，介绍在属性值为连续性和离散型下的两类常用的生成学习算法，分别是高斯判别分析(Guass Discrimination Analysis，GDA)和朴素贝叶斯(Bernoulli event model)。它们分别假设属性值的条件分布为多元正态分布和二项分布，它们可以应对大部分情形。最后我们进行适当的拓展，介绍属性值既有连续型又有离散型变量时的处理方法，多项分布下的朴素贝叶斯分类器，以及工程实现时采用的拉普拉斯平滑变换。

生成学习算法的基本思想

在之前的回归分类算法中，我们做的是建立一个直接预测标签值$y$的模型，即$h_{\theta }(x)=E(y|x)$。这样的分类算法亦称为判别学习算法(Discrimination Learning Algorithm)。但这里存在一个问题，即是我们用一个统一的模型对不同类别的属性值进行统一的处理，输出y的期望值。

基于问题的背景，判别学习算法的好坏是很难一言蔽之的，但是我们确实可以从另外一个角度来做分类，即我们在各个类别中根据类别的具体情况$y=y_i$建立属于这个类别的关于属性值$x$的条件分布$p_i(x|Y)=p_i(x|Y=y_i)$。因此，现在就可以利用贝叶斯后验概率公式来计算
$$\begin{array}{rl}P(Y=y_i|X=x_i)=& \frac{P(Y=y_i,X=x_i)}{P(X=x)}\\ =& \frac{P(Y=y_i)P(X=x_i|Y=y_i)}{p(X=x)}\end{array}$$然后，根据似然原理，我们选择概率最大的$y_i$作为预测的类别。
注意，广义来讲，不同的$y_i$对应的分布$p_i(x|y)$可以是不同形式的，但一般取相同的分布，而且只在一些参数上做区别。

高斯判别分析(Guass Discrimination Analysis)

GDA 的数学原理(为什么是线性判别？)

在属性值为连续型变量的情形下，我们可以假设其条件分布为多元正态分布，即$$p(x|Y=y_i)=\frac{1}{\sqrt{2\pi }|\Sigma {|}^{\frac{1}{2}}}exp((-\frac{1}{2})(x-{\mu }_i{)}^{{}^{\prime }}{\Sigma }^{-1}(x-{\mu }_i))$$这里我们假设不同的类别下的条件分布中，协方差矩阵$${\Sigma }_i=\Sigma ,i\in \{0,1,...,k-1\}$$从直观上讲，这实际上规定了不同类别之间属性值的分布形状是一致的，差别只在于所在中心位置$\mu$的不同，当然这是一个较强的假设，但是它让我们所需要估计的参数大大减少。

现在我们讨论两个类别的多维正态分布的情况。如果我们已经有训练数据获得估计出其中的参数${\varphi }_y=P(y=1),\Sigma ,{\mu }_0和{\mu }_1$。那么就可以利用似然比$$\alpha =\frac{p(y=1|x)}{p(y=0|x)}=\frac{{\varphi }_{y}p(x|y=1)}{(1-{\varphi }_y)p(x|y=0)}$$来分类。即
$$y=\{\begin{array}{r}1,\alpha >1\\ 决策边界,\alpha =1\\ 0,\alpha <1\end{array}$$对$\alpha$的形式进行适当的变形，我们记

$\theta =2({\mu }_0-{\mu }_1{)}^{{}^{\prime }}{\Sigma }^{-1}$，

${\theta }_0={\mu }_1^{{}^{\prime }}{\Sigma }^{-1}{\mu }_1-{\mu }_0^{{}^{\prime }}{\Sigma }^{-1}{\mu }_0-2log(\frac{\varphi (y)}{1-{\varphi }_y})$，

记超平面${\pi }_{01}$的方程为：
$${\theta }^{T}x+{\theta }_0=0$$通过简单的代数运算就可以发现上述依据似然比对y的分类等价于利用超平面${\pi }_{01}$进行分类，即：
$$y=\{\begin{array}{r}1,{\theta }^{T}x+{\theta }_0>0(落于超平面上方)\\ 决策边界,{\theta }^{T}x+{\theta }_0=0(落于超平面)\\ 0,{\theta }^{T}x+{\theta }_0<0(落于超平面下方)\end{array}$$特别的，当只有只有两个类别且${\varphi }_y=0.5时$，此时属性空间为一条直线，决策边界为一个点$$x=\frac{{\mu }_0+{\mu }_1}{2}$$

对于多个分类的情况，只需要进行两两比较即可。

GDA 的几何直观

在上面$\Sigma$相同的假设之下，我们已经证明，GDA实际是对属性值所在的空间做线性划分，因此在协差阵相同假设下的GDA也称为线性判别分析(Liner Discrimination Analysis,LDA)。在k个类别，n维正态分布下，LDA利用k个n维超平面将n维空间分割为k个区域。超平面上的点称为决策边界。特别地，在3个类别的2维正态分布中，有3条射线将平面分割为3个区域，其如下图所示：

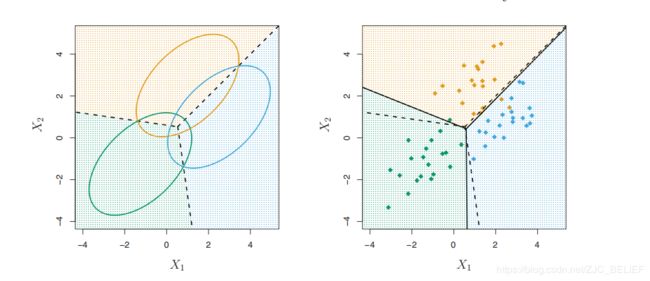
GDA 的参数估计

现在我们需要在已有的数据中，估计出${\varphi }_y=P(y=1),\Sigma ,{\mu }_0和{\mu }_1$。我们采用的仍是极大似然(MLE)的估计方法。似然函数为
$$L({\varphi }_y,\Sigma ,{\mu }_0,{\mu }_1;(X,Y))=\prod _{i=1}^m{\varphi }_y^{y^{(i)}}(1-{\varphi }_y{)}^{1-y^{(i)}}P(x^{(i)}|y=y^{(i)})$$其中 $$P(x^{(i)}|y=y^{(i)})=p_1(x^{(i)}|y)1\{y^{(i)}=1\}{p}_0(x^{(i)}|y)1\{y^{(i)}=0\}$$$1\{condition\}$表示的是当conditon为真时，取值为1，当conditon为假时，取值为0。

现在对数之，令$L$关于${\varphi }_y,\Sigma ,{\mu }_0,{\mu }_1$的各个偏导为0，记
$m_0={\sum }_{i=1}^{m}1\{y^{(i)}=0\}$
$m_1={\sum }_{i=1}^{m}1\{y^{(i)}=1\}$
即可解得：
$${\varphi }_y=\frac{m_1}{m}$$$${\mu }_0=\frac{{\sum }_{i=1}^m{x}^{(i)}1\{y^{(i)}=0\}}{m_0}$$$${\mu }_1=\frac{{\sum }_{i=1}^m{x}^{(i)}1\{y^{(i)}=1\}}{m_1}$$$$\Sigma =\frac{1}{m}\sum _{i=1}^m(x^{(i)}-{\mu }^{(i)})(x^{(i)}-{\mu }^{(i)}{)}^T$$

二次型判别分析(Quadratic Discrimination Analysis，QDA)

前面我们对GDA的讨论是基于二者具有相同的协差阵假设下的，我们看见该假设下的贝叶斯决策边界是线性的。现在我们讨论协差阵不同时的GDA。即：
$${\Sigma }_0不等于{\Sigma }_1$$在这种情况下，我们同样可以利用MLE估计出各个参数，其形式同上述是一致的，只需要在各个类别中对协差阵进行估计即可。
与LDA不同的是，此时的贝叶斯决策边界不是一个超平面，而是一个超二次曲面，特别的，在二维的情况下，它是一条抛物线(LDA下为一条直线)。通过简单的代数运算，我们可以得到该超二次曲面的数学解析式，我们记：

$A={\Sigma }_1^{-1}-{\Sigma }_0^{-1}$

$B=2({\mu }_0^T{\Sigma }_0^{-1}-{\mu }_1^T{\Sigma }_1^{-1})$

$C={\mu }_1^T{\Sigma }_1^{-1}{\mu }_1-{\mu }_0^T{\Sigma }_0^{-1}{\mu }_0+log(\frac{|{\Sigma }_1|}{|{\Sigma }_0|})-2log(\frac{{\pi }_0}{{\pi }_1})$

二次曲面${\pi }_{01}$为：
$$x^{T}Ax+Bx+C=0$$此时我们的判别等价于
$$y=\{\begin{array}{r}1,x^{T}Ax+Bx+C>0(落于超二次曲面上方)\\ 决策边界,x^{T}Ax+Bx+C=0(落于超二次曲面)\\ 0,x^{T}Ax+Bx+C<0(落于超二次曲面下方)\end{array}$$

朴素贝叶斯(Naive Bayes)

NB 的数学原理和朴素贝叶斯假设

通过生成学习算法的基本思想，我们已经知道，其重点和难点在于对确定每个类别的条件分布。
我们现在讨论有k个类别，n个离散型属性的情况。这里显然不适合利用多元正态分布作为属性值的条件分布。我们先假设每个离散型属性为二元取值，即取0或1，那么给定类别y后，整个属性值的可能取值就有$2^n$个，因此我们直接想到的就是利用多项分布作为属性值的条件分布，即$$P(X=x|Y=y_{)}=\prod _{i=1}^{2^n}{\varphi }_{i|y}^{1\{x=x_i\}}$$因此，我们总共需要估计$k(2^n-1)$。显然在属性值维度稍微大的时候，参数的数量就已经让我们无法承受了。

破解这个参数数量魔咒的就是朴素贝叶斯假设(Naive Bayes (NB) assumption)。朴素贝叶斯假设，假设属性值在每一个类别中的取值是独立的，即属性值是条件独立的，数学表达为：
$$p(x_i|y,x_j)=p(x_i|y)，j\in \{1,..i-1,i+1,...,k\}$$这使得条件分布的中参数数量从指数增长变成了线性增长，此时的参数数量为$n-1$。在朴素贝叶斯假设下的分类算法称为朴素贝叶斯分类器(Naive Nayes Classifier)。
当然朴素贝叶斯假设是比较强的，有时甚至不是很合理，比如在邮件垃圾分类中，对于一封已知是垃圾邮件的邮件而言，各个词的出现概率当然不会是完全独立的，比如我们知道某个词出现了，那么显然与这个词相关联的词出现的概率会提高。但在有限的样本量的情况，我们通过牺牲这样一些关联性可以减少极大地参数的个数，因此大部分情况朴素贝叶斯假设还是可以带来不错的分类效果。

朴素贝叶斯算法的参数估计

类似地，我们利用极大似然(MLE)对参数进行估计，我们首先讨论y有两个类别 ，每一个离散型属性为二元取值的情况，然后可以看到，稍加推广，参数估计的结果就可以用于多个类别，属性为多元取值的情况。

我们讨论的似然函数为：
$$L({\varphi }_y,{\varphi }_{j|y=1},{\varphi }_{j|y=0})=\prod _{i=1}^m{\varphi }_y^{y^{(i)}}(1-{\varphi }_y{)}^{1-y^{(i)}}$$其中$$P(x^{(i)}|y=y^{(i)})=\prod _{j=1}^n{\varphi }_{j|y=0}^{y^{(i)}{x}_j^{(i)}}(1-{\varphi }_{j|y=0}^{y^{(i)}}{)}^{1-x_j^{(i)}}{\varphi }_{j|y=1}^{y^{(i)}{x}_j^{(i)}}(1-{\varphi }_{j|y=1}^{y^{(i)}}{)}^{1-x_j^{(i)}}$$

同样，我们令$L关于{\varphi }_y,{\varphi }_{j|y=1},{\varphi }_{j|y=0}$的偏导为0，记
$m_0={\sum }_{i=1}^{m}1\{y^{(i)}=0\}$
$m_1={\sum }_{i=1}^{m}1\{y^{(i)}=1\}$
即可解得：
$${\varphi }_y=\frac{m_1}{m}$$$${\varphi }_{j|y=0}=\frac{{\sum }_{i=1}^{m}1\{x_j^{(i)}=1\wedge y^{(i)}=0\}}{m_0}$$$${\varphi }_{j|y=1}=\frac{{\sum }_{i=1}^{m}1\{x_j^{(i)}=1\wedge y^{(i)}=1\}}{m_1}$$
推广之，即在t个类别，每一个离散属性变量有k个取值时，参数的估计为：
$${\varphi }_{yt}=\frac{m_t}{m}$$$${\varphi }_{j|y=t}=\frac{{\sum }_{i=1}^{m}1\{x_j^{(i)}=1\wedge y^{(i)}=t\}}{m_t}$$

注：上述各式均具有明显的直观含义，读者可以自行解读。

拓展部分

连续与离散并存时的处理方法

当属性值取值即有离散型又有连续型时，我们可以将连续型的变量进行离散化(decretize)，从而利用朴素贝叶斯算法进行分类。离散化操作需要更具变量的具体背景进行设置。

拉普拉斯变换(Laplace smoothing)

为了处理一些异常偏僻属性值，我们在参数估计的数学解析式上进行适当的平滑处理，即：
$${\varphi }_{j|y=t}=\frac{{\sum }_{i=1}^{m}1\{x_j^{(i)}=1\wedge y^{(i)}=t\}+1}{m_t+k}$$

实战项目：利用LDA进行数据分类(python)

注：本例利用LDA进行分类，在属性值为连续的数据中，LDA的预测准确率高达95%，但在一些属性值明显不是连续取值的时候，LDA的预测效果是较差的，只有73%左右，这个时候我们或许可以利用朴素贝叶斯算法进行分类。
LDA的几个基本假设为：1. 属性数据是连续取值，2. 可视为多元正态分布，3. 各个类别的条件分布形状相同。当LDA效果不好时，可以从这些角度去思考，看看哪个假设差别甚远，从而考虑更合适的分类算法。

LDA.py

import numpy as np
from numpy import dot
from numpy.linalg import inv

def LDA_Estimate(X,Y,classNum):
    '''
    本函数利用MLE对LDA方法的参数进行估计
    输入参数：
    X: 样本属性数据
    Y: 样本标签数据
    classNum: 类别数
    返回估计的参数：
    meanMatrix: 均值矩阵p*k
    covMatrix: 协方差矩阵p*p
    priorVecter: 先验概率向量
    '''
    # 构造估计参数的矩阵结构
    meanMatrix = np.zeros((classNum,X.shape[1]))
    covMatrix = np.zeros((X.shape[1],X.shape[1]))
    priorVecter = np.zeros((classNum,1))
    # 计算均值矩阵p*k ，先验概率 prior
    for i in range(classNum):
        indexVexter = (Y == i)
        meanMatrix[i] = sum(X[indexVexter])/sum(indexVexter)
        priorVecter[i] = sum(indexVexter)/X.shape[0]  
    # 计算协差阵 Sigma
    for i in range(X.shape[0]):
        covMatrix = covMatrix + dot(X[i:(i+1)].T-meanMatrix[int(Y[i]):int(Y[i]+1)].T,X[i:(i+1)]-meanMatrix[int(Y[i]):int(Y[i]+1)])
    covMatrix = covMatrix/X.shape[0]
    # 返回结果
    return meanMatrix,covMatrix,priorVecter

def LDA_result(meanMatrix,covMatrix,priorVecter,classNum,X):
    '''
    本函数利用估计完的参数进行预测
    meanMatrix: 均值矩阵p*k
    covMatrix: 协方差矩阵p*p
    priorVecter: 先验概率向量
    classNum: 判别类别
    X: 属性样本数据
    '''
    # 初始化判别函数的参数 beta0
    beta0 = np.ones((classNum,1))
    # beta0 的计算公式： log(\pi_k) -1/2 * u_k^T * sigma^{-1} * u_k 
    for i in range(classNum):
        beta0[i] = dot(meanMatrix[i:i+1],dot(inv(covMatrix),meanMatrix[i:i+1].T))
    beta0 = -0.5*beta0 + np.log(priorVecter)
    # beta1 的计算公式
    beta1 = dot(meanMatrix,inv(covMatrix))
    # 输出结果向量，result[i] 表示第i个样本的判别类别
    result = np.ones(X.shape[0])
    for i in range(X.shape[0]):
        # deltaK 为判别函数在每一个类别的值
        deltaK = dot(beta1,X[i:i+1].T) + beta0、
        # 选择deltaK 中最大的值对应的索引为其判别类别
        result[i] = deltaK.argmax()
    return result

测试代码LDAtest.py

import numpy as np
import pandas as pd
import LDA

if __name__ == '__main__':
    # samData = pd.read_table('C:/Users/Administrator/Desktop/MLCourseOfWSQ/pythonProject/mlData/Logistic/TestSet.txt',
                           # header = None)
    samData = pd.read_table('C:/Users/Administrator/Desktop/MLCourseOfWSQ/pythonProject/mlData/Logistic/HorseColicTraining.txt',
                           header = None)
    # 样本数据的结构处理
    sample = np.array(samData)
    sampleY = sample[:,sample.shape[1]-1]
    sampleX = sample[:,0:sample.shape[1]-1]
    
    # 参数估计
    meanMatrix,covMatrix,priorVecter = LDA.LDA_Estimate(sampleX,sampleY,2)
    # 结果预测
    result = LDA.LDA_result(meanMatrix,covMatrix,priorVecter,2,sampleX)
    # 结果输出
    result = np.zeros(sample.shape[0])
    result[predictY>0.5] = 1
    compareResult = (sampleY == result)
    for i in range(sample.shape[0]):
        print('Y:',sampleY[i],'    Predict Y:',result[i],'    boolCompare:',compareResult[i])
    print('right discrimination number:',sum(compareResult))
    print('right discrimination ratio :',sum(compareResult)/sample.shape[0])