李宏毅机器学习笔记一
Contents
- 0 Introduction of this Course
- 1 Regression-Case Study
- 2 Where does the error come from?
- 3 Gradient Descent
- 4 Classification
- 5 Logistic Regression
- 6 Brief Introduction of Deep Learning
- 7 Backpropagation
0 Introduction of this Course
AI : 目标
Machine Learning :手段
Deep Learning:Machine Learning的一种方法
1 Regression-Case Study
Output a scalar (输出一个数值),这种任务属于Regression
Example Application
- Estimate the Combat Power (CP:战斗力) of a pokemon after evolution
机器学习的三大步骤:
-
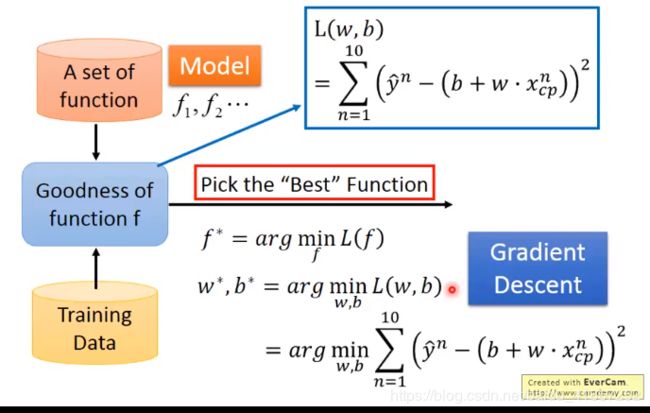
Step 1:Model

function set 又无数多个(infinite),其中有的合理,有的错误
图上属于线性模型
Linear Model : y = b + ∑ w i x i y=b+\sum w_ix_i y=b+∑wixi
x i x_i xi 称为特征(feature),将哪些特征带入模型,需要专业判断
w i w_i wi 称为权重
b b b 称为偏置 -
Step 2 : Goodness of Function(判断找出的函数有多好)

Training Data 中有多个数据,如 { ( x 1 , y ^ 1 ) , ( x 2 , y ^ 2 ) , … } \{(x^1,\hat{y}^1),(x^2,\hat{y}^2) ,\dots\} {(x1,y^1),(x2,y^2),…}
Training Data:
10 pokemons:
( x 1 , y ^ 1 ) (x^1,\hat{y}^1) (x1,y^1)
( x 2 , y ^ 2 ) (x^2,\hat{y}^2) (x2,y^2)
⋮ \vdots ⋮
( x 10 , y ^ 10 ) (x^ {10},\hat{y}^{10}) (x10,y^10)
画出10个点


代价函数,用于衡量function有多好或多不好
L ( w , b ) = ∑ n = 1 10 ( y ^ n − ( b + w ⋅ x c p n ) ) 2 L(w,b)=\sum_{n=1}^{10}(\hat{y}^n-(b+w\cdot x_{cp}^n))^2 L(w,b)=n=1∑10(y^n−(b+w⋅xcpn))2
使用梯度下降找最好的函数
代价函数图如下:
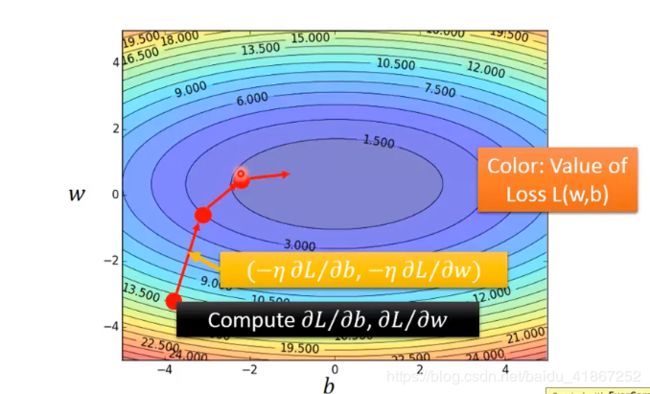
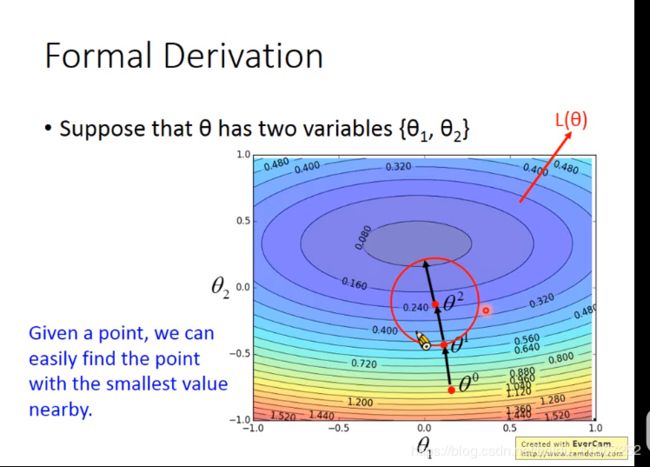
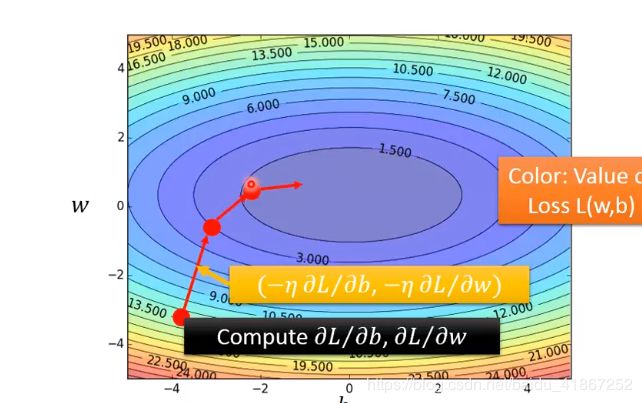
颜色越蓝,代价越小;梯度下降的方向是该点的等高线的法线方向
( − η ∂ L ∂ b , − η ∂ L ∂ w ) \left(- \eta\frac{\partial L}{\partial b}, - \eta\frac{\partial L}{\partial w} \right) (−η∂b∂L,−η∂w∂L)
然后不断的进行梯度下降
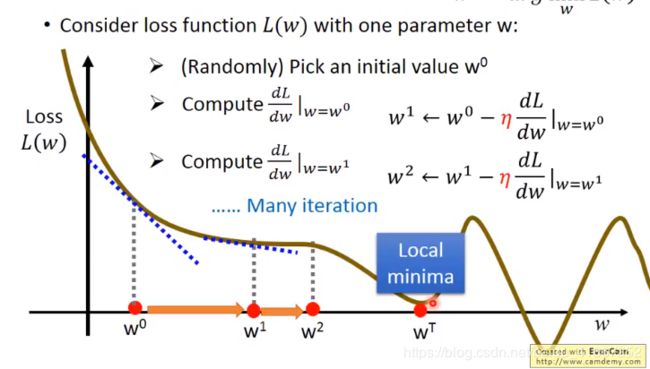
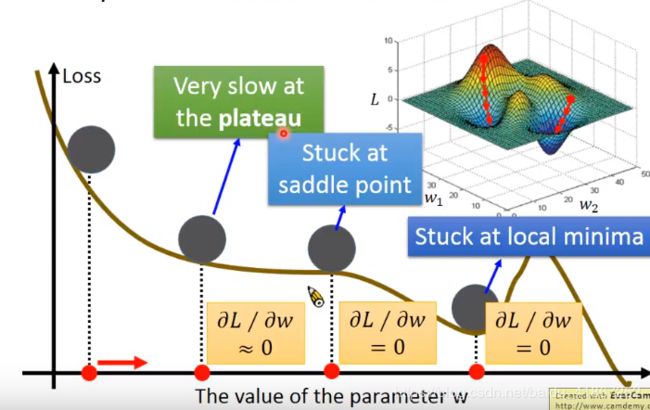
梯度下降可能存在的问题:1.陷入局部最小值(local minimum) 2.陷入鞍点(saddle point) 3.在偏导数很小时可能就结束了(plateau)
线性回归模型不用担心这类问题,题为其代价函数是碗状的,对于比较复杂的模型才需要考虑。
对 L ( w , b ) = ∑ n = 1 10 ( y ^ n − ( b + w ⋅ x c p n ) ) 2 L(w,b)=\sum_{n=1}^{10}\left(\hat{y}^n-(b+w\cdot x^n_{cp})\right)^2 L(w,b)=n=1∑10(y^n−(b+w⋅xcpn))2
∂ L ∂ w = − 2 ∑ n = 1 10 ( y ^ n − ( b + w ⋅ x c p n ) ) x c p n \frac{\partial L}{\partial w}=-2\sum_{n=1}^{10}\left(\hat{y}^n-(b+w\cdot x^n_{cp})\right)x^n_{cp} ∂w∂L=−2n=1∑10(y^n−(b+w⋅xcpn))xcpn
∂ L ∂ w = − 2 ∑ n = 1 10 ( y ^ n − ( b + w ⋅ x c p n ) ) \frac{\partial L}{\partial w}=-2\sum_{n=1}^{10}\left(\hat{y}^n-(b+w\cdot x^n_{cp})\right) ∂w∂L=−2n=1∑10(y^n−(b+w⋅xcpn))
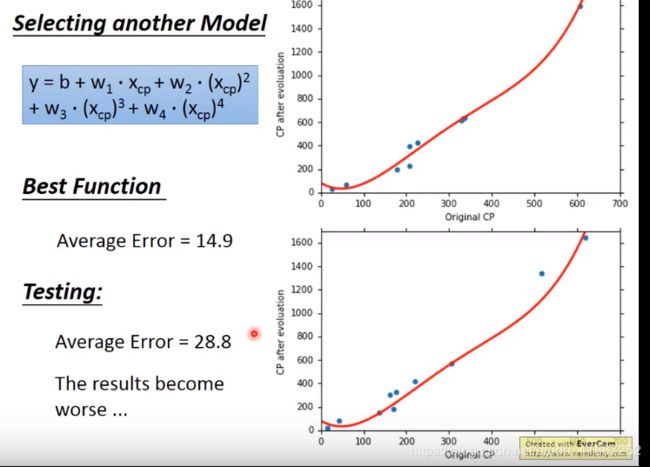
将得到的最好的函数画出来:
并计算出误差
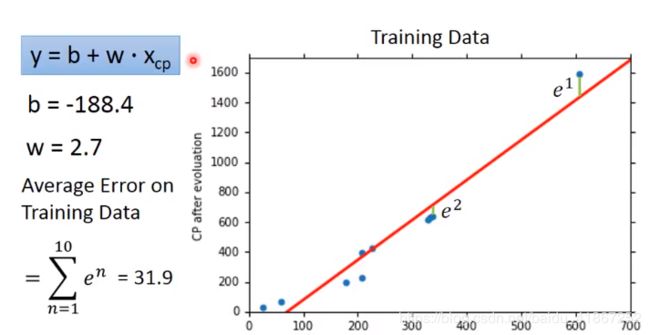
在测试数据上的表现如下:
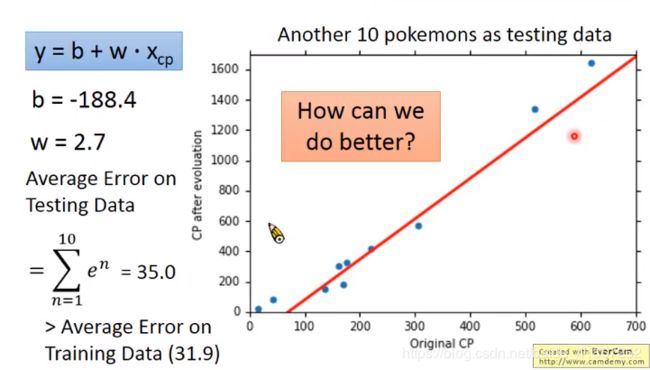
在testing data 上的误差值比training data 的误差高,是正常的。
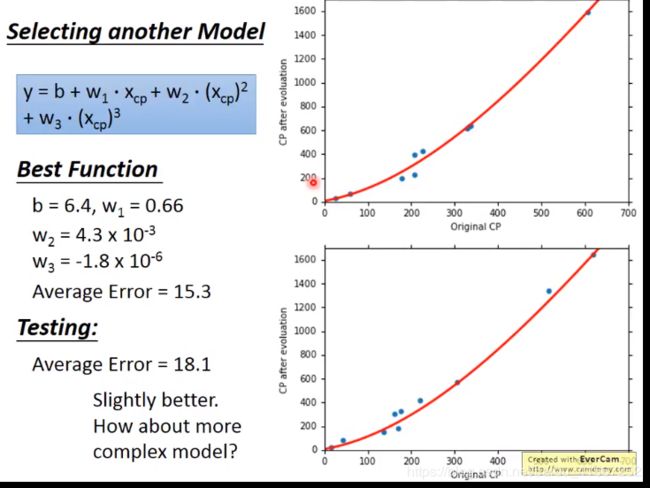
模型改进:
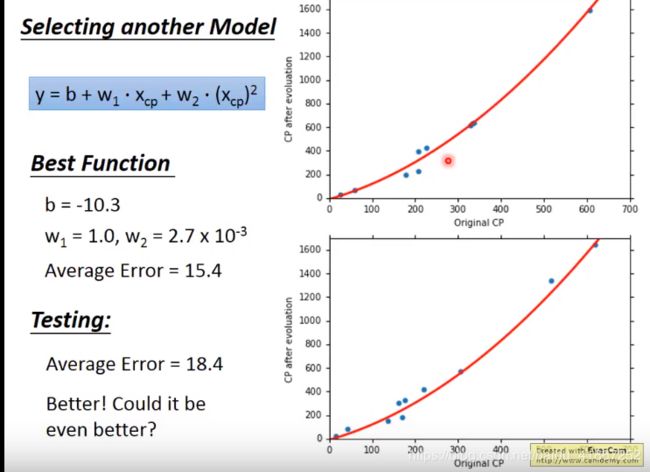
y = b + w 1 ⋅ x c p + w 2 ⋅ ( x c p ) 2 y=b+w_1\cdot x_{cp}+w_2\cdot (x_{cp})^2 y=b+w1⋅xcp+w2⋅(xcp)2 仍然是线性模型(取决于参数对输出是线性的,如, b , w 1 , w 2 b,w_1,w_2 b,w1,w2), ( x c p ) 2 (x_{cp})^2 (xcp)2可以看成是新特征。
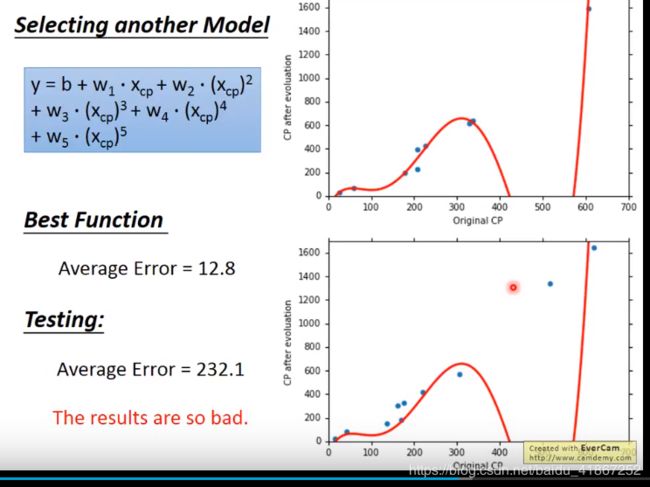
模型改进:
显然,模型越复杂,在training data 上表现越好

圆圈包含关系,表示低次是高次的子集,自然高次的误差小
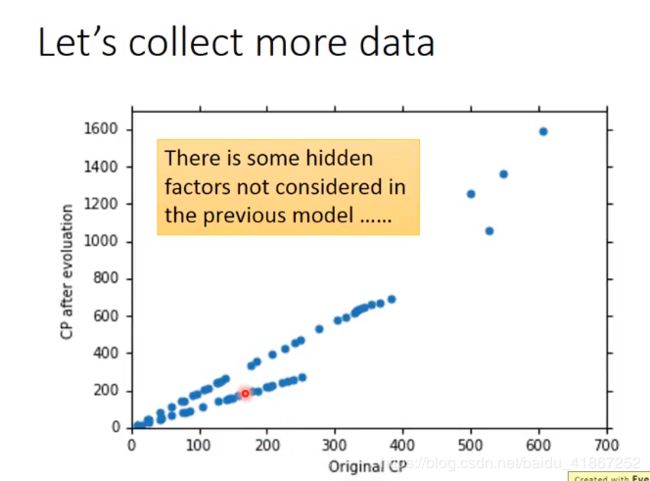

需要将polemon的种类考虑在内,才能更好地预测。
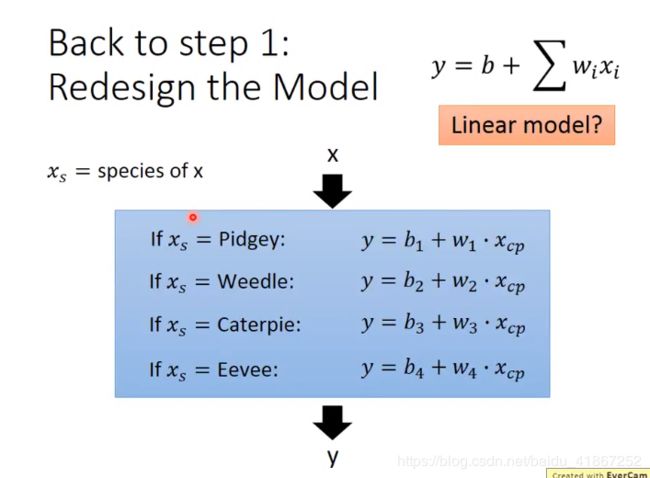
换种写法

如果 x s = P i d g e y , 则 y = b 1 + w 1 ⋅ x c p x_s=Pidgey,则 y=b_1+w_1\cdot x_{cp} xs=Pidgey,则y=b1+w1⋅xcp
还有其他的hidden factors ,因为不确定是哪几个,就都加进来:
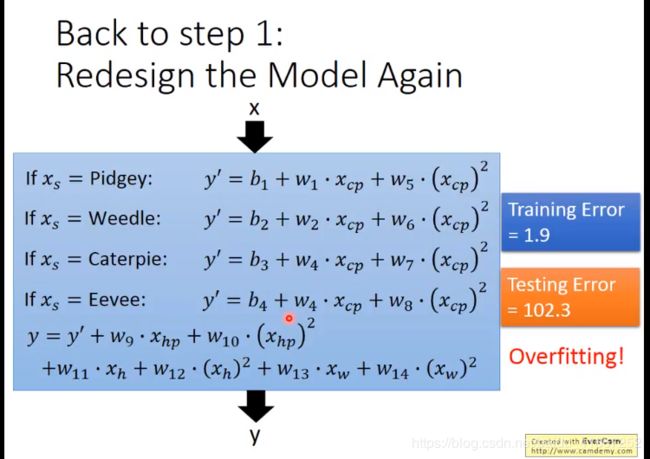
(第3行 w 4 改 成 w 3 w_4改成w_3 w4改成w3 )
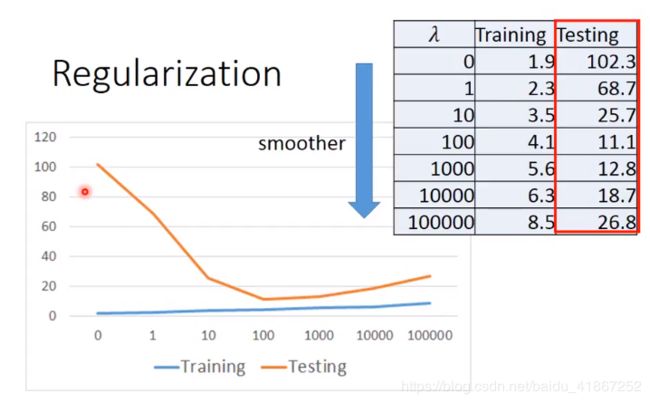
此时导致过拟合,应使用正则化

注:
- smoother意味着,给自变量一个增量 Δ x i \Delta x_i Δxi,输出的增量 ∑ w i Δ x i \sum w_i\Delta x_i ∑wiΔxi 较小
- 平滑的结果更可能是正确的
- 偏置 b b b 不需要正则化,因为是一个直线,不会影响到平滑性
- λ \lambda λ 越大(显然 w i w_i wi越小),function 越平滑
- λ \lambda λ 越大,训练集误差越大
- 想要平滑的函数,但不能过于平滑,所以要选择合适的 λ \lambda λ,此例 λ = 100 \lambda=100 λ=100较好
2 Where does the error come from?
μ \mu μ 是数学期望,是总体的平均
X 1 , … , X N 与 总 体 是 同 分 布 的 , 所 以 E ( X ˉ ) = E ( 1 N ∑ X i ) = 1 N N E ( X ) = E ( X ) = μ X_1,\dots,X_N与总体是同分布的,所以E(\bar X )=E(\frac{1}{N}\sum X_i)=\frac1{N}NE(X)=E(X)=\mu X1,…,XN与总体是同分布的,所以E(Xˉ)=E(N1∑Xi)=N1NE(X)=E(X)=μ
X ˉ \bar{X} Xˉ 是若干样本的平均
σ 2 \sigma^2 σ2 是总体的方差
s 2 s^2 s2 是样本的方差
s 2 = 1 N − 1 ∑ ( X i − X ˉ ) 2 s^2=\frac{1}{N-1}\sum(X_i-\bar{X})^2 s2=N−11∑(Xi−Xˉ)2 该式是对总体方差的无偏估计,此时才有 E ( s 2 ) = σ 2 E(s^2)=\sigma^2 E(s2)=σ2
模型误差来源有:bias, variance(偏差和方差)
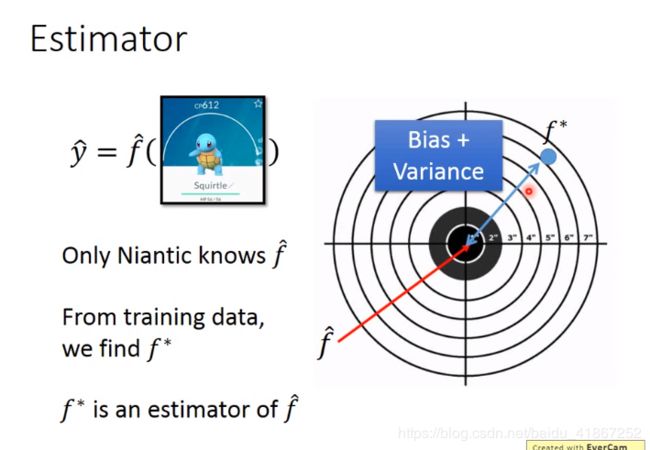
f ^ \hat f f^ 是未知的,我们只能找出 f ∗ f^* f∗, f ∗ f^* f∗ 是对 f ^ \hat f f^ 的估测

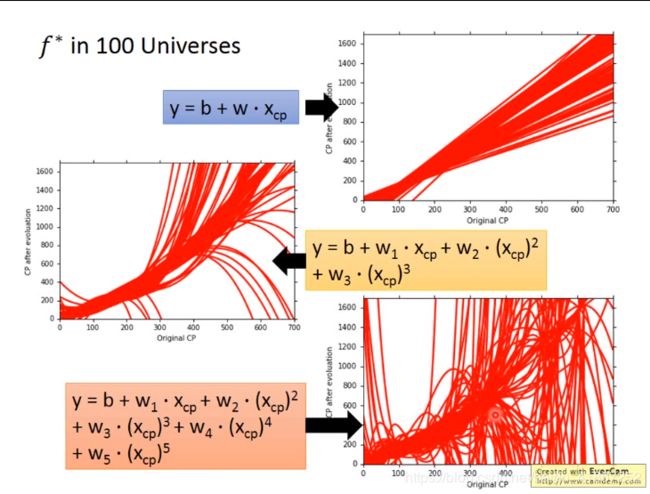
方差:越复杂的模型,越容易受到样本数据的影响(复杂的模型放大了误差)
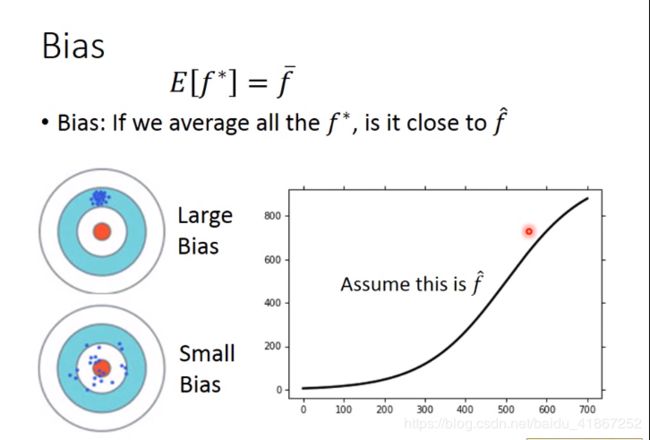


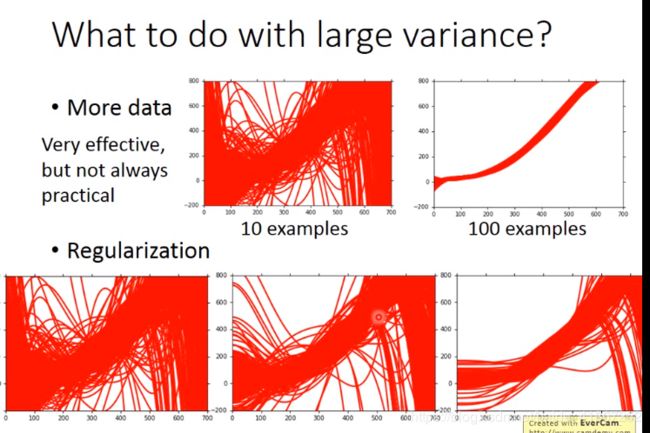
上图下方, λ \lambda λ 依次增大。正则化可能会损害bias,因此亚要选择合适的 λ \lambda λ
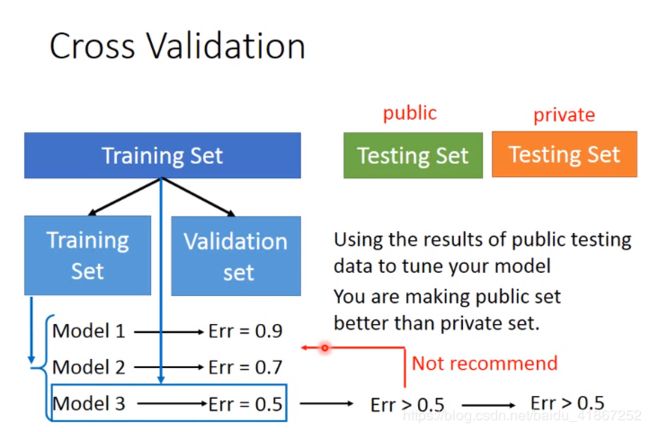
cross validation 交叉验证
在 Training Set 中分一部分作为 Validation set
用Training set 训练模型, 用Validation set 选出最合适的一个模型(在其上误差小的)
选出模型后,再用整个 Training Set 训练该模型
发现在public testing set 上误差较大,此时能反映在private testing set上的误差
不建议用public testing set 再训练模型,这样会在模型中加入public testing set 的偏差,以至于在public testing set上的性能(performance)与private testing set上的表现不同

上面的这种方式,划分training set 和validation set 较好,选出平均误差最小的 model,再用整个 Training Set 训练该模型
3 Gradient Descent
在 步骤3中,要做的是:
θ ∗ = a r g min θ L ( θ ) \theta^*=arg \min_{\theta}L(\theta) θ∗=argθminL(θ)
假设 θ = [ θ 1 θ 2 ] \theta=\begin{bmatrix} \theta_1\\ \theta_2\end{bmatrix} θ=[θ1θ2]
初始化, θ 0 = [ θ 1 0 θ 2 0 ] \theta^0=\begin{bmatrix} \theta_1^0\\ \theta_2^0\end{bmatrix} θ0=[θ10θ20]
Δ L ( θ ) = [ ∂ L / ∂ θ 1 ∂ L / ∂ θ 2 ] \Delta L(\theta)=\begin{bmatrix}\partial L/\partial \theta_1\\\partial L/\partial \theta2\end{bmatrix} ΔL(θ)=[∂L/∂θ1∂L/∂θ2]


上图表明,梯度下降的方向,是梯度的反方向。

红线:学习速率刚刚好
蓝线:学习速率较小(收敛速度太慢)
绿线:学习速率较大(得不到最优值)
黄线:学习速率太大(得不到最优值)
当参数个数大于等于3个,就无法可视化参数-代价得图,但代价-迭代次数总能画出。

adagrad 是 adaptive learning rate 的一种方法

adagrad 保证每个参数得学习速率都不同
adagrad具体步骤如下

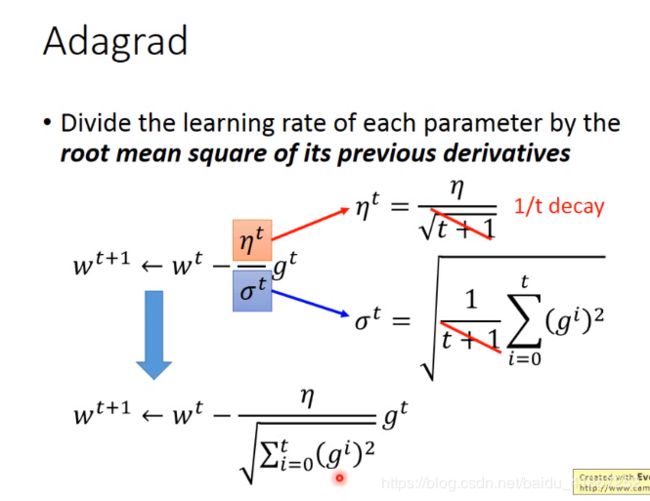

上图表明,一次导数越大,步伐就越大(仅一个参数时适用)

a点一次导小于c点的,而a点的步伐却大于c点的
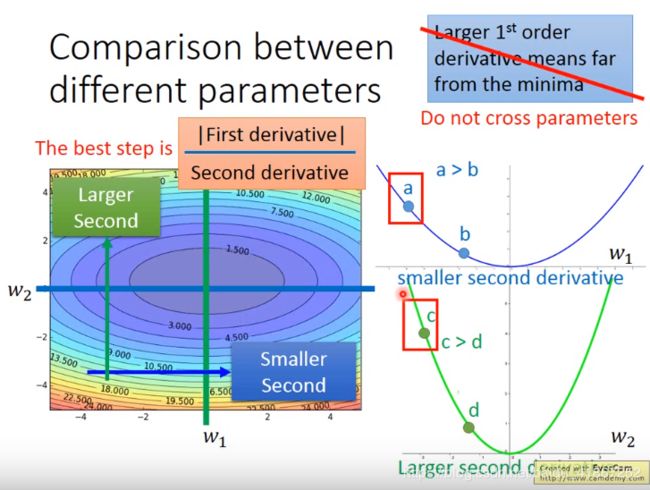

用一阶导近似代替二阶导,看图知二阶导数大,其一阶导数各点和也较大。
- Gradient Descent 的代价函数
L ( θ ) = ∑ n ( y ^ n − ( b + ∑ i w i x i n ) ) 2 L(\theta)=\sum_n(\hat{y}^n-(b+\sum_i w_ix_i^n))^2 L(θ)=n∑(y^n−(b+i∑wixin))2
-
gradient descent 和 stochastic gradient descent对比

gradient descent 运算量大,较慢,但稳定
stochastic gradient descent 运算量小,速度快,可能不会收敛,在最小值附近波动 -
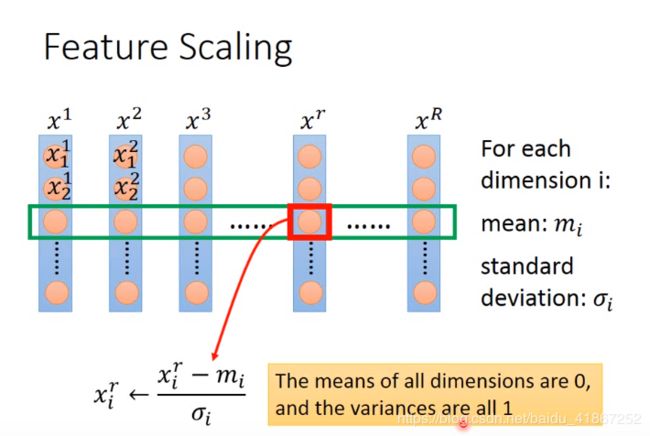
Feature Scaling
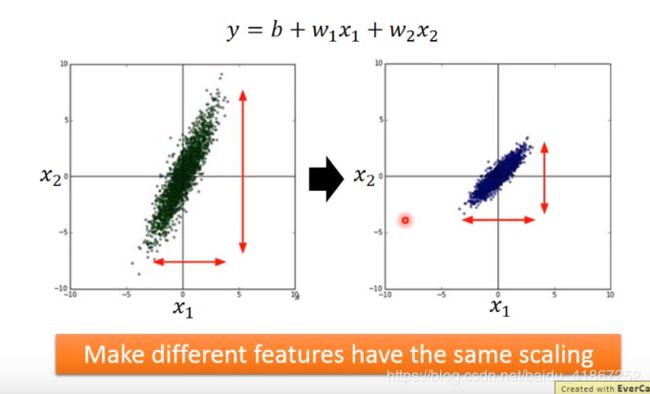
使不同的特征,有相同的尺寸

x 1 x_1 x1 的取值范围较小, W 1 W_1 W1 的变化,对代价的影响也较小,所以上图水平方向变化平缓。

上图左侧,梯度下降沿着等高线的法线,并不指向椭圆的圆心,收敛速度慢;
上图右侧,梯度下降始终指向圆心,收敛速度快
u Δ θ 1 + v Δ θ 2 = ( u , v ) ⋅ ( Δ θ 1 , Δ θ 2 ) = a ⃗ ⋅ b ⃗ = ∣ a ⃗ ∣ ∣ b ⃗ ∣ cos ( a ⃗ , b ⃗ ^ ) u\Delta\theta_1+v\Delta\theta_2=(u,v)\cdot(\Delta\theta_1,\Delta\theta_2)=\vec{a}\cdot\vec{b}=\vert\vec{a}\vert\vert \vec{b}\vert\cos(\widehat{\vec{a},\vec{b}}) uΔθ1+vΔθ2=(u,v)⋅(Δθ1,Δθ2)=a⋅b=∣a∣∣b∣cos(a,b )
所以,当 ( u , v ) 与 ( Δ θ 1 , Δ θ 2 ) (u,v) 与 (\Delta\theta_1,\Delta\theta_2) (u,v)与(Δθ1,Δθ2)方向相反时, L L L 减少得最快


上式就是梯度下降,学习速率必须小,否则不适用。
如果考虑二次项,用牛顿法,此法计算量太大
4 Classification
x → x\rightarrow x→ function → \rightarrow →class n
回归问题得例子:




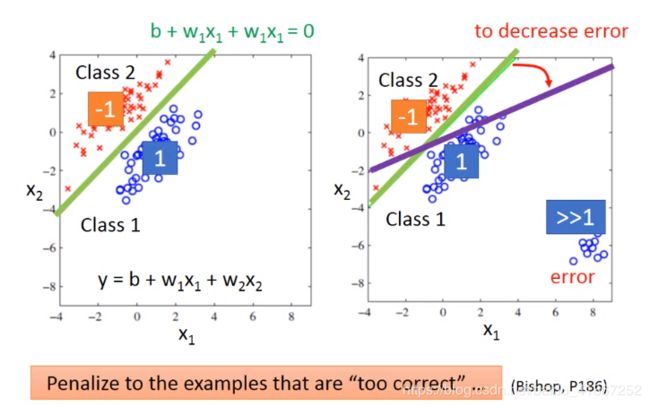

上式 L L L 不可到导
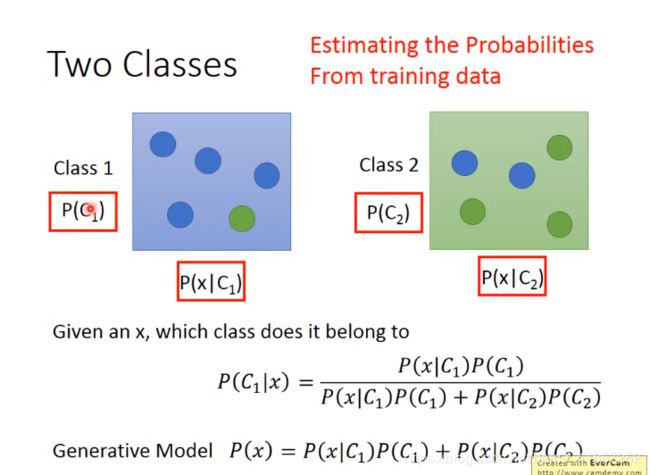
generative model 生成模型


第一行得宝可梦不再79个之中

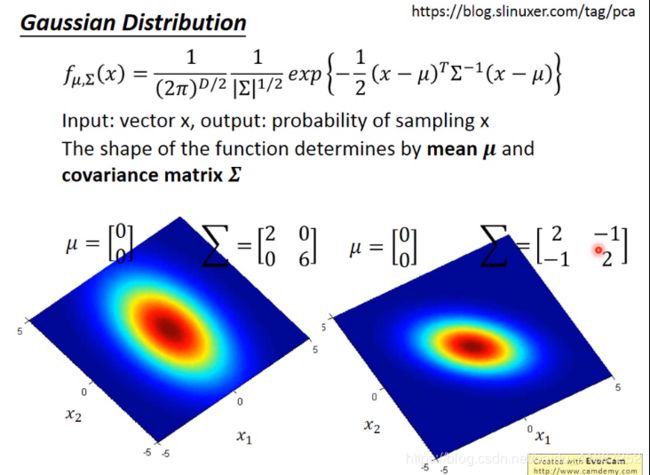
协方差矩阵 ∑ \sum ∑ 是一个对称矩阵,决定了二维高斯分布的形状。
对角线元素分别为x和y轴的方差
反斜对角线上的两个值为协方差,表明x和y的线性相关程度(正值时:x增大,y也随之增大;负值时:x增大,y随之减小)
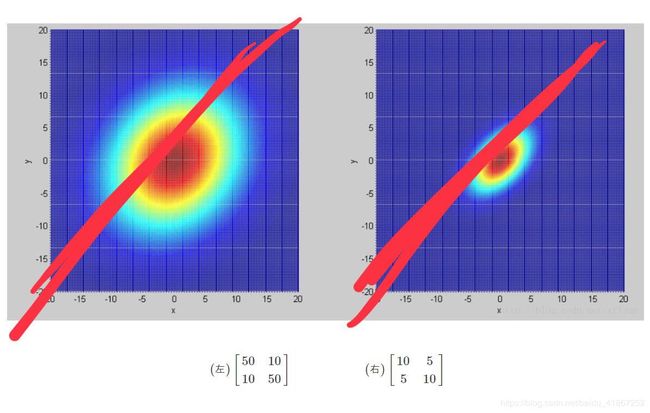

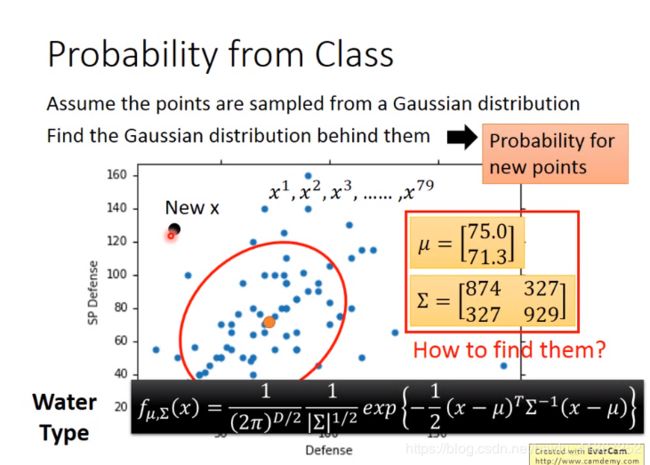

不同得Gaussian Distribution 都右可能产生这79个点,我们想找出其中可能性最大的。
Maximum Likelihood 极大似然估计
likelihood 可能性

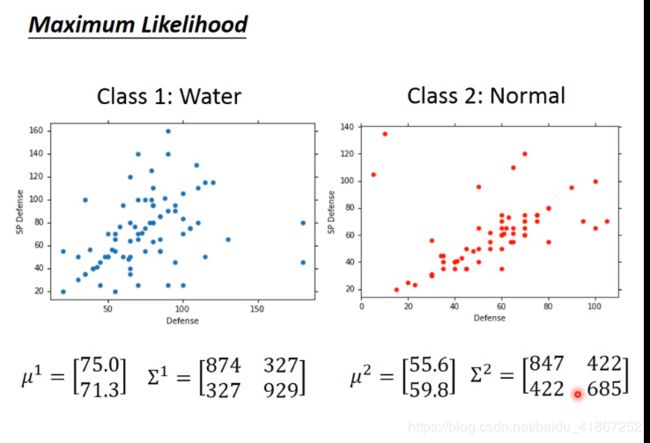

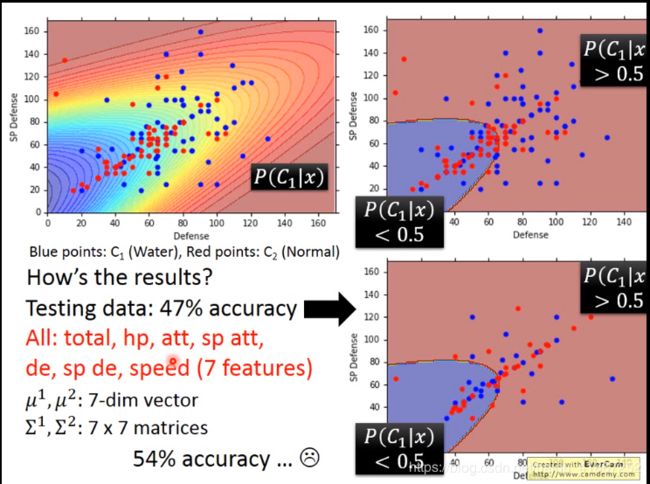
左上方图,黄色区域代表属于 water 得可能性大。
此时分类效果不好,边界不明显

公用协方差,可以减少参数数量,防止过拟合

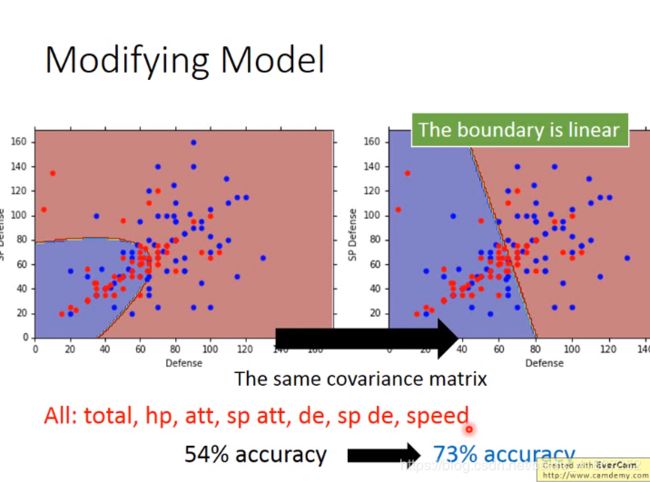


可以选择其他的概率模型
假设特征间是独立的,朴素贝叶斯效果好,不成立,则效果差

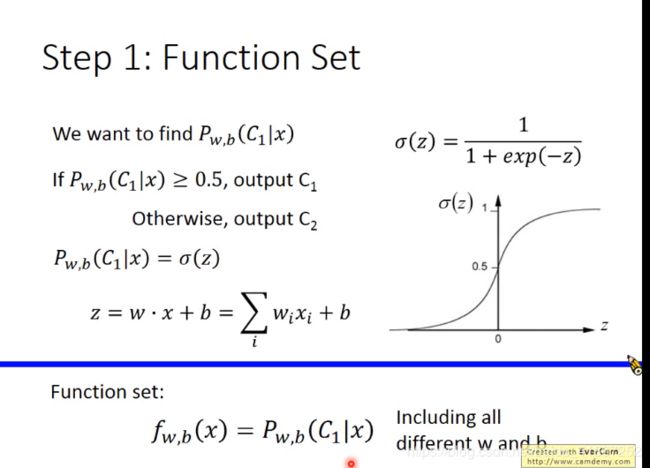
上图是由后验概率推导出sigmoid函数




其中b是常数

5 Logistic Regression
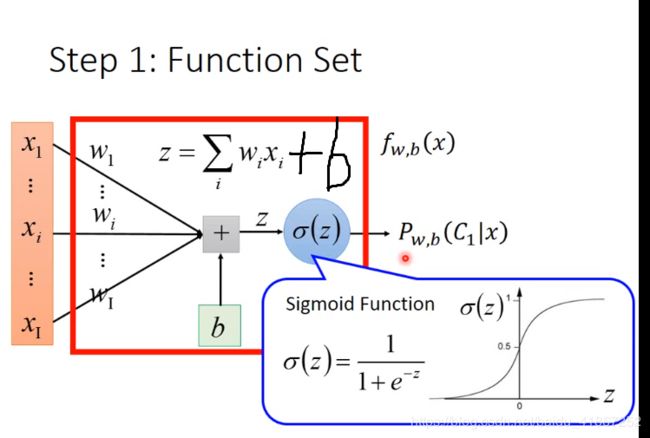



进一步
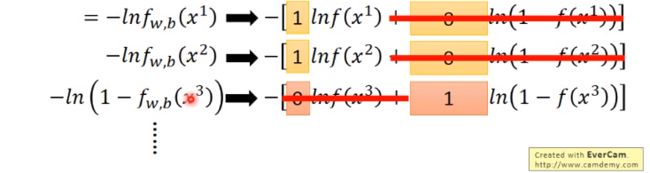
上式的好处: 无论x属于哪一类,都可以写成相同的形式
交叉熵表示两个分布有多接近,如果两者完全相同,交叉熵为0

![]()
∂ L ∂ w i = ∑ n [ f ( x n ) − y ^ n ] x i n \frac{\partial L}{\partial w_i}=\sum_n[f(x^n)-\hat{y}^n]x_i^n ∂wi∂L=n∑[f(xn)−y^n]xin
logistic regression 不能用误差平方和作为代价,解释如下:

当 y ^ n = 1 \hat{y}^n=1 y^n=1,且 f w , b ( x n ) = 1 , ⟹ ∂ L ( f ) ∂ w i = 0 f_{w,b}(x^n)=1, \Longrightarrow \frac{\partial L(f)}{\partial w_i}=0 fw,b(xn)=1,⟹∂wi∂L(f)=0,是合理的
当 y ^ n = 1 \hat{y}^n=1 y^n=1,且 f w , b ( x n ) = 0 , ⟹ ∂ L ( f ) ∂ w i = 0 f_{w,b}(x^n)=0, \Longrightarrow \frac{\partial L(f)}{\partial w_i}=0 fw,b(xn)=0,⟹∂wi∂L(f)=0,不合理。距离目标越远,更新步伐应越大,即偏导越大

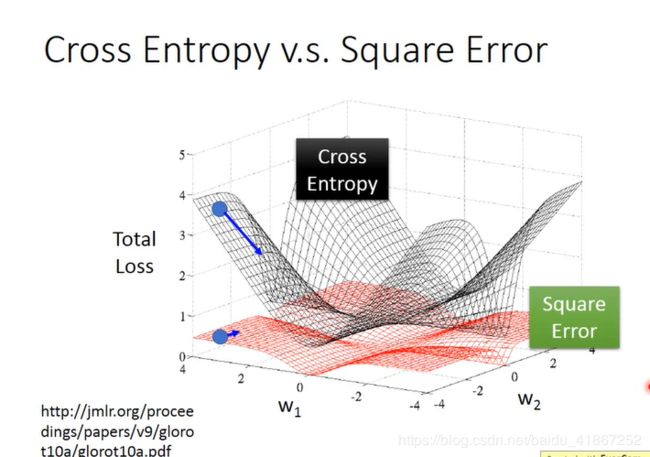
“square error”中,当远离和接近最小点时,偏导都很小,不利于更新参数

在生成模型中,假设了概率分布模型,如高斯或伯努利或朴素贝叶斯(特征是离散的,假设各特征是独立的),又假设协方差矩阵相同。
两个模型产生的w,b是不同的。
![]()
上图可视化中,只用了两个特征,两个模型优劣不容易看出,拓展到多维后,发现discriminative model 效果更好

使用判别模型的做法:
![]()
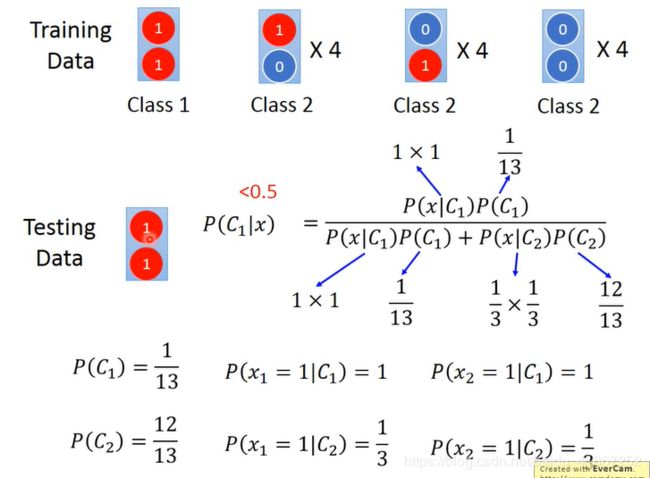

生成模型的优势:数据较少时可以使用;对噪音比较健壮(如上例,将两个1分类为class 2 ,即理解为噪音)



逻辑回归不能解决异或问题

进行特征转换可以解决,然而转换方式并不容易发现
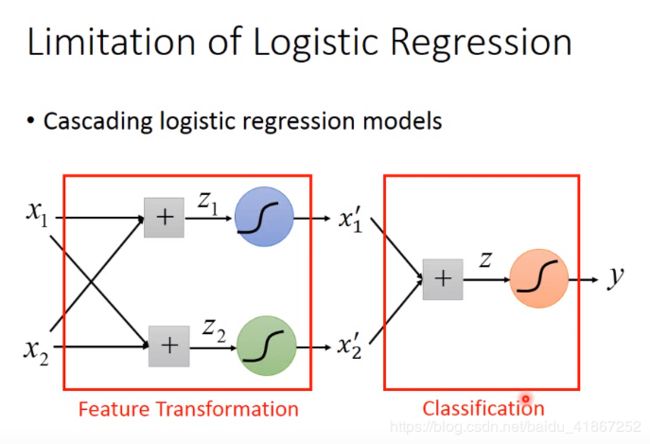
特征转换可以看成是多个logistic regression 叠加一起(相当于加了一个一个隐藏层)
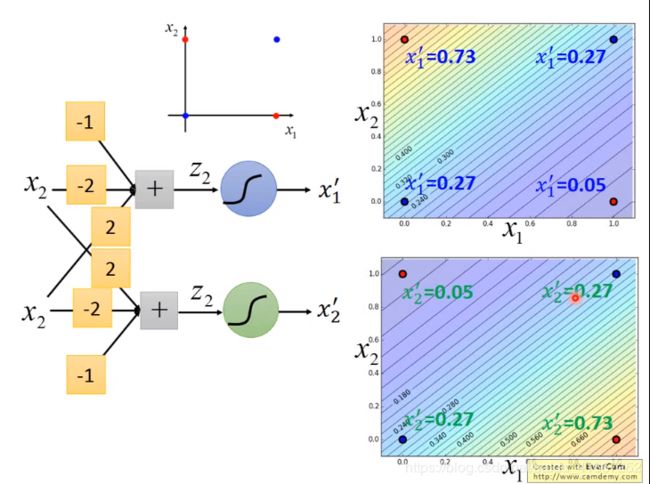

所有的参数可以共同学习
6 Brief Introduction of Deep Learning


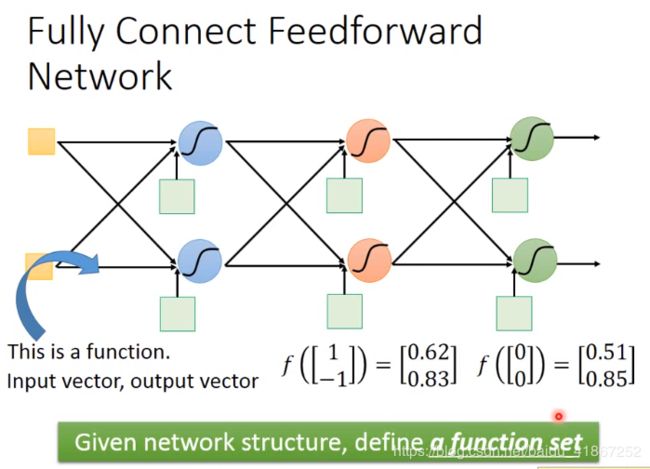
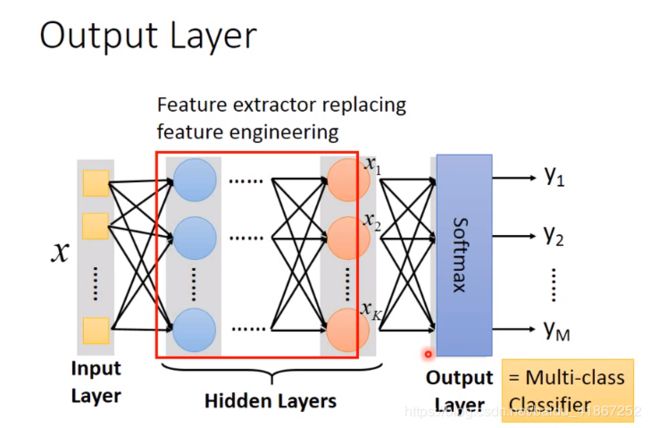
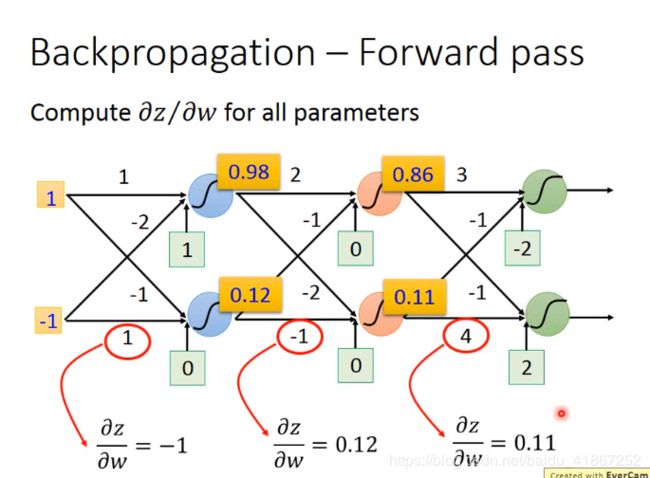
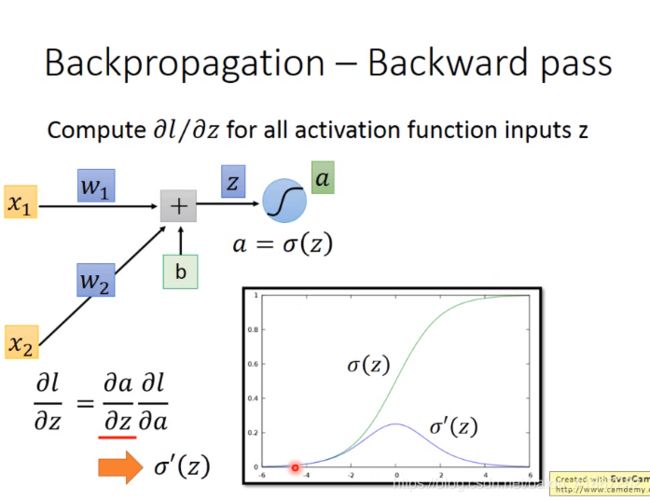
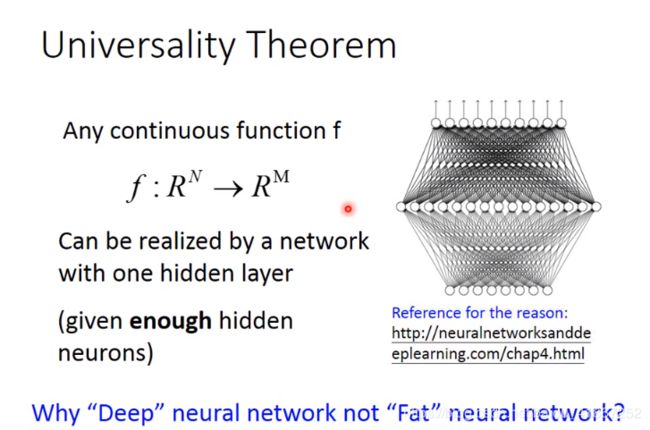
![]()
x 1 , x K x_1,x_K x1,xK看成是提取后的新特征