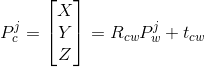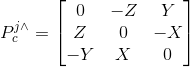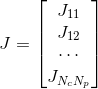爽一把手写Bundle Adjustment
今天是传说中的5.20,同时也是本人最近特别钟爱的神剧《权力的游戏》大结局的日子,作为一名伪技术宅,这么重大的日子当然要写一篇文来纪念一下。所以就有了这篇手写Bundle Adjustment的记录文。
Bundle Adjustment(后面简写成BA)在视觉SLAM里面的作用不用多说,自然是非常重要的。BA主要求解的是一个关于相机位姿以及路标点的空间坐标的大规模最小二乘优化问题,每一个相机位姿都与多个路标点关联,而每一个路标点也同时和多个相机位姿相关联,由此形成复杂的网状的相互约束,通过调整相机位姿和路标点的位置估计,使得所有路标点在所有相机中的重投影误差最小。下面我们就来亲自动手尝试一下求解Bundle Adjustment。相关的理论可以参考《视觉SLAM十四讲》第六章和第十章,这里仅简单略过。
1 Levenberg-Marquardt优化
考虑简单的最小二乘优化问题:
将![]() 进行一阶泰勒展开:
进行一阶泰勒展开:
![]()
同时通过拉格朗日乘子添加对增量的约束,得到以下形式:
对![]() 求导并令导数等于0,可得以下方程
求导并令导数等于0,可得以下方程
![]()
求解以上增量方程,可得![]() 的值,进而令
的值,进而令![]() 更新对优化变量
更新对优化变量![]() 的估计。
的估计。
在实际应用中通常取![]() 或者
或者![]() ,同时还涉及到对
,同时还涉及到对![]() 大小的调整。
大小的调整。
在应用Levenberg-Marquardt优化算法时,最主要的步骤就是求函数值![]() 和雅可比
和雅可比![]() ,以及求解增量方程得出
,以及求解增量方程得出![]() 。
。
下面尝试一下Ceres优化库的一个曲线拟合的实例![]() 。拟合用的数据点通过对真实曲线
。拟合用的数据点通过对真实曲线![]() 进行采样并附加标准差
进行采样并附加标准差![]() 的高斯噪声生成。
的高斯噪声生成。
#include
#include
//用来生成高斯噪声
std::default_random_engine e;
std::normal_distribution n(0, 0.2);
//用来存储数据点
std::vector> data;
//生成数据点,假设x的范围是0-5
for(double x = 0; x < 5; x += 0.05)
{
double y = exp(0.3*x + 0.1)+n(e);
data.push_back(std::make_pair(x, y));
} 根据以上数据点拟合曲线的最小二乘优化问题为
令![]() ,则
,则
![]()
#include
#include
using namespace std;
using namespace Eigen;
//为了方便,先定义每一项f(m,c)的误差与雅可比,
//整体的F(m,c)与雅可比J(m,c)可以通过将每个小块组合起来得到
class FitErrorBlock
{
public:
FitErrorBlock(double x, double y) :x_(x), y_(y) {}
double function(double m, double c)
{
return (exp(m*x_ + c) - y_);
}
Eigen::Matrix Jacobian(double m, double c)
{
Eigen::Matrix J;
J[0] = x_ * exp(m*x_ + c);
J[1] = exp(m*x_ + c);
}
double x_, y_;
};
//接下来开始Levenberg-Marquardt优化
class LMOptimization
{
public:
//设置初值
void setInitValue(double m, double c)
{
m_ = m;
c_ = c;
}
//优化算法主体
void Optimize(int niters)
{
double lambda = 1e-4;
for (int iter = 0; iter < niters; iter++)
{
//构造雅可比和函数值向量,将每一项作为一行
MatrixXd Jacobian(errorTerms.size(), 2);
VectorXd err(errorTerms.size());
for (int k = 0; k < errorTerms.size(); k++)
{
err[k] = errorTerms[k]->function(m_, c_);
Jacobian.row(k) = errorTerms[k]->Jacobian(m_, c_);
}
//构造增量方程
Matrix2d JTJ = Jacobian.transpose()*Jacobian;
Matrix2d A = JTJ + lambda * Matrix2d(JTJ.diagonal().asDiagonal());
Vector2d b = -Jacobian.transpose()*err;
//求解增量方程Ax=b
Vector2d delta=A.colPivHouseholderQr().solve(b);
//如果增量幅度小于阈值,则认为已经收敛,停止优化
if (delta.norm() < 1e-10)
{
break;
}
//计算更新前后的误差
double err_before = 0.5*err.squaredNorm();
double err_after = 0;
for (int k = 0; k < errorTerms.size(); k++)
{
double e= errorTerms[k]->function(m_ + delta[0], c_ + delta[1]);
err_after += e * e;
}
err_after *= 0.5;
//判断是否接受更新,如果更新后的误差减小,则接受更新,同时减小lambda;否则不接受更新,并增大lambda
if (err_after < err_before)
{
m_ += delta[0];
c_ += delta[1];
lambda /= 10;
err_before = err_after;
}
else
{
lambda *= 10;
}
cout << "iteration = " << iter << ", error = " << err_before << " , lambda = " << lambda << endl;
}
}
void addErrorTerm(FitErrorBlock* e)
{
errorTerms.push_back(e);
}
double m_, c_;
//保存最小二乘优化的每一项
std::vector errorTerms;
}; 在调用优化算法的时候,可以简单地将每一项加入到优化函数里面
int main()
{
std::default_random_engine e;
std::normal_distribution n(0, 0.2);
std::vector> data;
for (double x = 0; x < 5; x += 0.05)
{
double y = exp(0.3*x + 0.1)+n(e);
data.push_back(std::make_pair(x, y));
}
LMOptimization opt;
for (int k = 0; k < data.size(); k++)
{
FitErrorBlock *e = new FitErrorBlock(data[k].first,data[k].second);
opt.addErrorTerm(e);
}
opt.setInitValue(0, 0);
opt.Optimize(50);
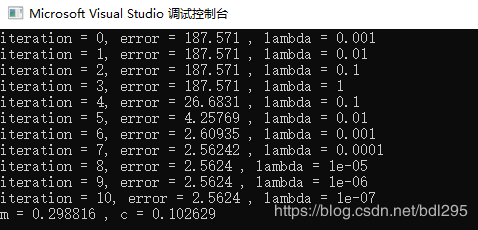
cout << "m = " << opt.m_ << " , c = " << opt.c_ << endl;
return 0;
} 结果如下
2 求解Bundle Adjustment
从以上实例可以看出,求解最小二乘优化主要分为四步:计算每一个误差项及其雅可比,将所有误差项组合起来构造增量方程,求解增量方程,更新优化变量。用相同的思想来求解BA,首先要定义每一个误差项以及雅可比,然后利用BA的稀疏结构构建增量方程并求解,最后增新优化变量。
在BA里面比较常见的就是路标点在图像里面的重投影误差,为了方便计算雅可比,这里采用“预测值-测量值”的形式。
![]()
class ReprojectionError
{
public:
//位姿采用旋转矩阵与平移向量表示
typedef pair CameraPose;
ReprojectionError() :fx(0), fy(0), cx(0), cy(0), u(0), v(0), camIdx(0), pointIdx(0)
{
;
}
void setMeasurement(double u, double v)
{
this->u = u;
this->v = v;
}
void setCameraParams(double fx, double fy, double cx, double cy)
{
this->fx = fx;
this->fy = fy;
this->cx = cx;
this->cy = cy;
}
//计算重投影误差
Vector2d function(const CameraPose cam,const Vector3d p)
{
Matrix3d R = cam.first;
Vector3d t = cam.second;
Vector2d error;
Vector3d pc = R * p + t;
double xp = pc[0] / pc[2];
double yp = pc[1] / pc[2];
double up = f * xp + cx;
double vp = f * yp + cy;
error[0] = up - u;
error[1] = vp - v;
return error;
}
Matrix Jacobian(const CameraPose cam,const Vector3d p)
{
Matrix J;
Matrix3d R = cam.first;
Vector3d t = cam.second;
Vector3d pc = R * p + t;
double x = pc[0], y = pc[1], z = pc[2];
double z2 = z * z;
Matrix J_e_pc;
J_e_pc << f / z, 0, -f * x / z2,
0, f / z, -f * y / z2;
Matrix J_pc_ksi;
J_pc_ksi << Matrix3d::Identity(), -skew(pc);
//对相机位姿的雅可比
Matrix J_e_ksi = J_e_pc * J_pc_ksi;
Matrix3d J_pc_p = R;
//对路标点位置的雅可比
Matrix J_e_p = J_e_pc * J_pc_p;
J << J_e_ksi, J_e_p;
return J;
}
Matrix3d skew(Vector3d phi)
{
Matrix3d Phi;
Phi << 0, -phi(2), phi(1),
phi(2), 0, -phi(0),
-phi(1), phi(0), 0;
return Phi;
}
double fx, fy, cx, cy; //保存相机内参
double u, v; //路标点在图像上的测量值
int camIdx, pointIdx; //哪个相机观测哪个路标点
}; 在定义好了每一个误差项之后,接下来就是将各个误差项组合成一个大的雅可比和增量方程。
整体的雅可比可以看作是一个以每个误差项对应的雅可比作为一行的分块矩阵
其中每一项雅可比块仅有两个非零子块
而![]() 也仅有四个子块非零,分别对应
也仅有四个子块非零,分别对应![]() 、
、![]() 、
、![]() 、
、![]() 四个位置。最终累加得到的
四个位置。最终累加得到的![]() 具有特殊的稀疏结构
具有特殊的稀疏结构
其中![]() 和
和![]() 均为分块对角阵,
均为分块对角阵,![]() 。
。
在进行累加的时候,可以利用以下特点:
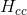 中的每个分块均为
中的每个分块均为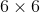 ,分块个数等于相机的个数;每一个
,分块个数等于相机的个数;每一个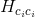 由
由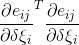 对所有的
对所有的 累加得到.
累加得到.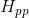 中的每个分块均为
中的每个分块均为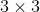 ,分块个数等于路标点的个数;每一个
,分块个数等于路标点的个数;每一个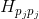 由
由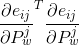 对所有的
对所有的 累加得到.
累加得到.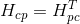 中的每个分块均为
中的每个分块均为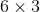 ,行数等于相机的个数,列数等于路标点的个数;每一个
,行数等于相机的个数,列数等于路标点的个数;每一个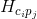 由
由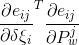 得到.
得到.
所以在计算时,可以对每一个误差项求出来![]() 和
和![]() 后,根据下标
后,根据下标![]() 和
和![]() 的值,分别将
的值,分别将![]() 、
、![]() 和
和![]() 累加到对应的
累加到对应的![]() 、
、![]() 和
和![]() 中去。类似地,误差向量和增量方程右端项也可以通过累加得到。下面的代码计算了增量方程的左端和右端,其中右端根据左端的分块对应地分成了
中去。类似地,误差向量和增量方程右端项也可以通过累加得到。下面的代码计算了增量方程的左端和右端,其中右端根据左端的分块对应地分成了![]() 和
和![]() ,分别对应于相机和路标点。
,分别对应于相机和路标点。
for (int k = 0; k < ErrorTerms.size(); k++)
{
ReprojectionError* term = ErrorTerms[k];
Matrix J = term->Jacobian(cameras[term->camIdx], points[term->pointIdx]);
Matrix Jc = J.block(0, 0, 2, 6);
Matrix Jp = J.block(0, 6, 2, 3);
Matrix JcTJc = Jc.transpose() * Jc;
Hcc[term->camIdx] += JcTJc + lambda * JacobianCC(JcTJc.diagonal().asDiagonal());
Matrix JpTJp = Jp.transpose() * Jp;
Hpp[term->pointIdx] += JpTJp + lambda * JacobianPP(JpTJp.diagonal().asDiagonal());
Hcp[term->camIdx][term->pointIdx] += Jc.transpose()*Jp;
Vector2d error = term->function(cameras[term->camIdx], points[term->pointIdx]);
bc[term->camIdx] -= Jc.transpose()*error;
bp[term->pointIdx] -= Jp.transpose()*error;
} 接下来最能利用BA特殊结构的时候到了,求解增量方程,主要利用了Schur消元。
消去右上角的![]() ,可以得到
,可以得到
第一行变成了和![]() 无关的方程,可以直接求解
无关的方程,可以直接求解![]() ,
,
![]()
因为通常![]() 维数比
维数比![]() 低很多,而且
低很多,而且![]() 为分块对角阵,每一个分块均为3阶方阵,很容易求逆,所以求解相对较快。在求得
为分块对角阵,每一个分块均为3阶方阵,很容易求逆,所以求解相对较快。在求得![]() 之后,
之后,![]() 可以将
可以将![]() 代入求得
代入求得
![]()
在计算和求解上述两个方程时,也可以根据之前的结论将计算过程转化为维数较低的分块矩阵进行累加,避免进行大型矩阵的运算。具体过程不再详细写出来了,将![]() 、
、![]() 和
和![]() 以及
以及![]() 和
和![]() 分别写成分块的形式,直接进行分块运算就可以了。
分别写成分块的形式,直接进行分块运算就可以了。
void ComputeUpdate()
{
int Nc = cameras.size();
int Np = points.size();
MatrixXd B(6 * Nc, 6 * Nc); //保存Hcc-HcpHpp^(-1)Hcp^(T)
vector InvHpp(Np); //保存Hpp^(-1)的各个分块
vector ECbp(Nc,Vector6d::Zero()); //保存HcpHpp^(-1)bp
VectorXd b(6 * Nc); //保存bc-HcpHpp^(-1)bp
//对Hpp各个分块求逆
for (int k = 0; k < Np; k++)
{
InvHpp[k] = Hpp[k].inverse();
}
//先将B赋值为Hcc,然后再减去HcpHpp^(-1)Hcp^(T)
for (int k = 0; k < Nc; k++)
{
B.block(6 * k, 6 * k, 6, 6) = Hcc[k];
}
//计算Hcc-HcpHpp^(-1)Hcp^(T)和HcpHpp^(-1)bp
for (int k = 0; k < Np; k++)
{
for (int i = 0; i < Nc; i++)
{
Matrix EikCk = Hcp[i][k] * InvHpp[k];
ECbp[i] += EikCk * bp[k];
for (int j = i; j < Nc; j++)
{
B.block(6 * i, 6 * j, 6, 6) -= EikCk * Hcp[j][k].transpose();
}
}
}
//因为B为对称矩阵,所以上面只计算了上三角部分,下三角部分直接赋值
for (int i = 0; i < Nc; i++)
{
for (int j = i+1; j < Nc; j++)
{
B.block(6 * j, 6 * i, 6, 6) = B.block(6 * i, 6 * j, 6, 6).transpose();
}
}
//计算bc-HcpHpp^(-1)bp
for (int k = 0; k < Nc; k++)
{
b.segment(6 * k, 6) = bc[k] - ECbp[k];
}
cout << "Solving Pose updates." << endl;
//求解delta xc
VectorXd deltac=B.colPivHouseholderQr().solve(b);
for (int k = 0; k < Nc; k++)
{
deltacs[k] = deltac.segment(6 * k, 6);
}
//回代求delta xp
for (int j = 0; j < Np; j++)
{
Vector3d Ekdeltack = Vector3d::Zero();
for (int i = 0; i < Nc; i++)
{
Ekdeltack += Hcp[i][j].transpose()*deltacs[i];
}
deltaps[j] = InvHpp[j] * (bp[j] - Ekdeltack);
}
cout << "Update Calculated." << endl;
} 最后对相机和路标点的估计进行更新,路标点的坐标直接按向量相加,相机位姿采用李代数运算左乘更新。
for (int k = 0; k < cameras.size(); k++)
{
CameraPose X = cameras[k];
Vector6d deltaX = deltacs[k];
Matrix4d deltaT = SE3Type::exp(deltaX);
Matrix3d deltaR = deltaT.block(0, 0, 3, 3);
Vector3d deltat = deltaT.block(0, 3, 3, 1);
Matrix3d Rnew = deltaR * X.first;
Vector3d tnew = deltaR * X.second + deltat;
camerasUpdated[k] = make_pair(Rnew, tnew);
}
for (int k = 0; k < points.size(); k++)
{
pointsUpdated[k] = points[k] + deltaps[k];
}其余部分均和第1部分Levenberg-Marquardt优化的过程完全相同,包括判断更新前后误差变化、对lambda的增减、判断收敛等,此处不再赘述。完整的代码放在了github上面。
https://github.com/BruceWhiteSJTU/CSDN-Blog/tree/master/Bundle%20Adjustment
参考文献
[1] 高翔,张涛.视觉SLAM十四讲[M].北京:电子工业出版社,2017.
[2]Timothy D.Barfoot.State Estimation for Robotics[M].United Kingdom:Cambridge University Press,2017.
[3]Grisetti G , Ku,Mmerle R , Stachniss C , et al. A Tutorial on Graph-Based SLAM[J]. IEEE Intelligent Transportation Systems Magazine, 2010, 2(4):31-43.
[4]Triggs B . Bundle Adjustment -A Modern Synthesis[J]. 1999.
[5]Frank D , Michael K . Factor Graphs for Robot Perception[C]// 2017:1-139.