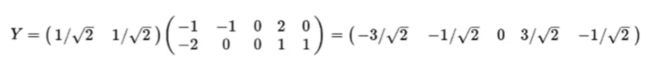sklearn 数据预处理，数据降维之特征选择，PCA主成分分析

目录

1.数据集的维度

2.什么是数据集降维

3.数据降维的方式

4.特征选择

1.特征选择的原因

2.特征选择是什么

3.特征选择的主要方法

4.Filter（过滤式）: VarianceThreshold

5.PCA主成分分析

sklearn对pca的支持

---

1.数据集的维度

何为维度？对于一组数据集，其特征的数量即为改组数据的维度；如[90,2,10,40]这样一组数据的维度即为4

2.什么是数据集降维

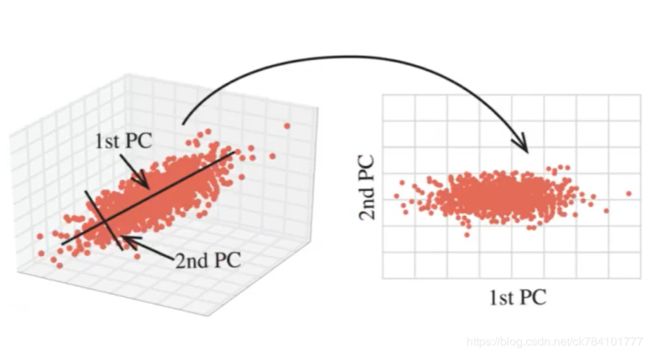
如图所示，左边的一组数据为三维数据，假设其三个特征为x,y,z，假设不考虑z特征（想象将一组三维的点向下拍平成二维的点，使的z=0），则可得到右图的一组数据，数据集由三维变为二维，而将数据集从高维转换到低维的这一行为叫做数据降维。

3.数据降维的方式

数据降维的两大方式为：

• 特征选择
• 主成分分析

下面详细介绍一下这两种方法是如何工作的

4.特征选择

1.特征选择的原因

数据冗余

特征选择的的第一个原因是为了削减数据冗余，在一组特征数据中，部分特征的相关度较高，当这样相关度高的特征较多时，就会造成过多的计算性能消耗；

数据噪声

第二个原因是特征去噪，在一组特征中，有一部分特征对推测目标值没有丝毫帮助，这种对分析目标值没有帮助的特征，就交租数据噪声。比如，以下是两只狗，它们有以下特征，我们希望根据这些特征来分析出它们的品种。

a.毛色 b.眼睛宽度 c.是否有尾巴 d.是否有爪子 e.嘴巴长度 

这组特征中，cd（是否有尾巴或爪子）对分析结果没有任何帮助，因为我们已经知道它们是狗，它们它们必定有爪子和尾巴，而它们是否有爪子和尾巴并不能推断出它们是和品种。所以我们需要做特征选择，过滤掉一些无关紧要的特征，这就叫数据降噪（也叫降维）。

 

2.特征选择是什么

特征选择就是单纯地从提取到的所有特征中选择部分作为训练集特征，特征在选择前和选择后可以改变值，也可以不改变值（特征预处理），但是选择后的特征维数肯定比选择前小。

3.特征选择的主要方法

• Filter（过滤式）: VarianceThreshold
• Embedded（Embedded）：正则化，决策树
• Wrapper（包裹式）

4.Filter（过滤式）: VarianceThreshold

过滤式比较好理解，就是将相同或比较接近的特征过滤掉，如下列一组数据，他们的第三特征(第三列）都是10，则可以过滤掉。

或是第四特征（第四列），它们之间的偏差只有1，也可以过滤掉。这么来说似乎不太专业，事实上，我们需要计算它们的方差，将方差为0,或1（可以人为指定），第三列的方差显而易见是1，第四列的方差则为0.66，在VarianceThreshold算法中，可以规定某特征方差在小于多少时进行过滤。

[90,2,10,40],
[60,4,10,41],
[75,3,10,39]

提示：因根据实际情况选择方差的过滤范围 

使用sklearn库进行过滤式处理

sklearn过滤式算法的API：sklearn.feature_selection.VarianceThreshold

from sklearn.feature_selection import VarianceThreshold

def filter():
    var = VarianceThreshold(threshold=1)
    data=var.fit_transform([[90,2,10,40],
                           [60,4,10,41],
                           [75,5,10,39]])
    print(data)

if __name__=="__main__":
     filter()

 VarianceThreshold()函数中的参数threshold=1 指定方差在0到1直接的特征被过滤掉

 

5.PCA主成分分析

什么是PAC

PCA是一种分析、简化数据集的技术，其核心在于数据维度压缩，以此尽可能降低原数据的维度，缺点是过多的数据降维可能损失信息，称为数据失真。通过PCA可以实现削减回归分析或者聚类分析中特征的数量。

适用场景

当特征数量较少时是不推荐使用PCA的，只有当特征数量达到上百上千时，才考虑对数据进行简化。图片的特征数量通常上千，此时就适合做主成分分析，再比如分析巨量数据时，如医学领域，金融市场领域。

PCA做了什么

假设有一组数据集，有100个特征，我们发现其中个别特征具有相似性，如下特征50恰好是特征1的2倍。所以当特征数量足够多的时候，特征直接不可避免有相似性，所以需要用到PCA对数据进行降维，将相似的特征进行处理后得到一个公共特征，这个公共特征即贴近与特征1又贴近与特征2。相较于特征选择算法来说，PCA是对相似特征进行处理，而特征选择是对单个特征进行处理（比如满足该特征下的数据集方差等于0）。

特征1 特征2 特征3 特征4 .... 特征50 特征51 特征52 特征53 .... 特征100  

 1                                              2              

 2                                              4

 3                                              6

 4                                              8

 5                                              10

 6                                              12 

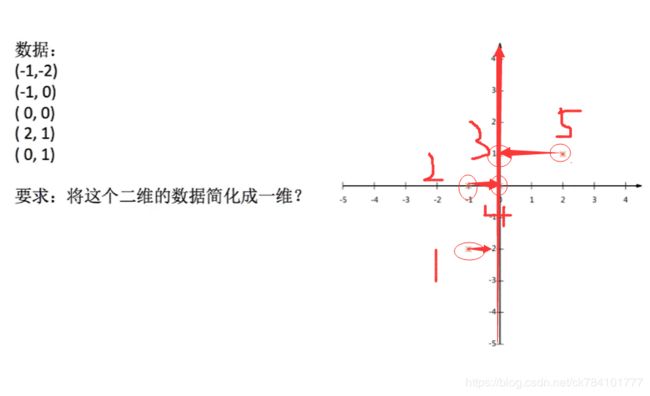
再举一个列子，考虑将一组二维数据集降维成一维数据集，在降维的过程中尽可能不丢失特征数量。

如图所示，我们试着将特征映射到x轴行，或者说将二维数据映射到一维的线上，但是问题来了，特征3和特征4在映射后重叠了，这就导致这一组数据失去了一个特征。

又或者将点映射到y轴上，也可以看到特征2和特征4重叠。

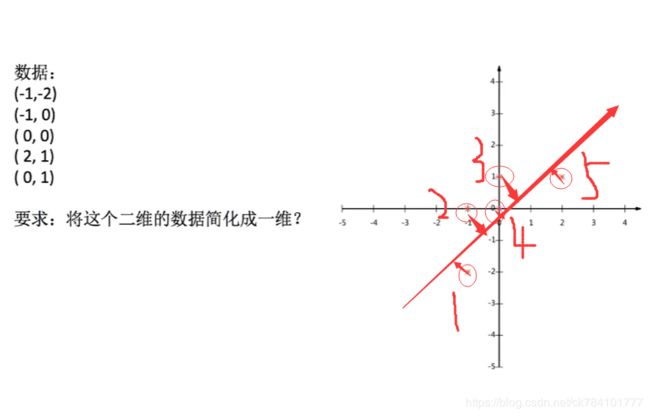
如果做到数据降维而有不损失特征呢？这就是PCA要做的事情，如图所示，我们划出一道所有特征映射到其上而不重叠的线，这样我们即实现了数据降维，又保留了所有特征。 

 

如何将上述点映射到线上，或者换一个说法，怎么找到一条线，它可以使得所有点映射到其上不损失特征（或损失少量特征）的呢？

设有公式Y=PX

其中P是一个矩阵，因为是二维的数据所以又有：Y=k1X+k2X

经过计算得出，计算出满足条件的k1,k2有两组：

 

那么Y：

 而PCA将这一切都封装进它的算法库中，对我们来说，拿来使用即可。

 

sklearn对pca的支持

API接口：sklearn.decomposition import PCA

from sklearn.decomposition import PCA

def pca():
    p=PCA()
    data=p.fit_transform([[90,2,10,40],
                           [60,4,19,45],
                           [75,8,13,46]])
    print(data)

if __name__=="__main__":
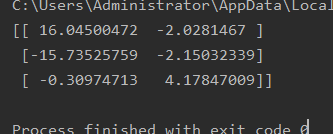
     pca()

进过降维后，得到一组三维数据，这组数据没有实际意义，但是他确实能代表被降维前的数据集。可调整n_components来获取最佳的降维后数据集。

 

补充：PCA()构造函数可填入n_components参数,n_components可选择小数或者整数。

小数的取值范围是0-1，比如90%，即保留原始数据集90%的信息。

或者填入整数，假如有一组4维数据，试图降到3维，则可填3。

PCA(n_components=0.99),保留99%的信息，则：

PCA(n_components=0.95),则：