第五章:重抽样方法
重抽样方法
- 第五章:重抽样方法
- 5.1 交叉验证法(cross-validation)
- 5.1.1验证集方法(validation set approach)
- 5.1.2 留一交叉验证法(leave-one-out cross-validation,LOOCV)
- 5.1.3 K折交叉验证(k-fold CV)
- 5.1.4 k折交叉验证的偏差-方差权衡
- 5.1.5 交叉验证法在分类问题的应用
- 5.2 自助法(bootstrap)
- 5.3 具体代码实现(R语言版本)
- 5.3.1验证集方法
- 5.3.2 k-fold CV方法
- 5.3.3 Bootstrap
- 5.4 结语:
第五章:重抽样方法
- 在之前的学习中,我们学了很多关于因变量是一个定量变量的回归模型,包括线性回归,KNN模型等,也学了很多因变量是定性变量的分类模型,这些模型也很优秀的解决了许多现实生活的预测与推断解释的问题。但是在现实的数据挖掘中,我们怎么去评价一个模型的好坏,或者选择更好的模型呢?评价一个模型的表现的过程被称为 模型评价(model assessment),而为一个模型选择合适的光滑度(复杂度)的过程被称为 模型选择(model selection) 。重抽样方法给大家提供了有效的方法。
- 下面我们举个例子说明下什么是重抽样方法:
比如:为了估计一个线性回归拟合模型的波动性,我们可以反复地从训练数据中抽取不同的样本,对每一个新的样本拟合一个线性回归模型,然后考察模型作适度扩展后对拟合结果会有怎么样的影响。这样的方法可以获得那些只用原始的训练样本来拟合模型所没有的信息。 - 所以我们现在来给重抽样方法起个定义吧:
重抽样方法通过反复从训练集中抽取样本,然后对每一个样本重新拟合一个感兴趣的模型,来获得关于拟合模型的 附加信息。 - 重抽样方法是现代统计学中不可或缺的工具,但是这类方法会产生 计算量上的代价,因为要用同一种统计方法对训练数据的不同子集拟合多次,但是随着计算机计算能力的改善,大部分重抽样方法的计算要求已经不成问题。在本章中,我们讨论两种最常用的重抽样方法: 交叉验证法(cross-validation) 和 自助法(bootstrap)。
5.1 交叉验证法(cross-validation)
- 在前面的学习中,我们主要探讨了测试错误率 (test error rate)和训练错误率(training error rate)的区别。测试误差是用一种统计学习方法在预测一个新的观测上(在训练模型中没有用到的一个观测)的响应值所产生的的平均误差。但是测试误差一般很难得到,而训练误差是很容易计算的,不过训练错误率通常跟测试错误率有很大的差别,尤其是训练错误率很可能会低估测试错误率。
- 为了解决测试误差率很难得到与训练误差率跟测试误差率差异较大的问题,我们的思路一般有两个:
(1).通过数学修正Cp , AIC ,BIC等将训练错误率修正估计训练错误率。(下一章重点讲解)
(2).在拟合过程保留训练观测的一个子集,然后对保留的观测运用统计学习方法,从而估计其测试误差率。(本章核心重点)
在本章中,我们会使用回归模型来讲解,对于分类模型其原理一样。
(下图为一般模型的训练误差及测试误差与模型复杂度的关系)

5.1.1验证集方法(validation set approach)
-
验证集方法(validation set approach)的步骤:
(1).随机地把观测集合分成两部分:训练集(training set) 和 测试集(validation set)或保留集(hold-out set)。
(2).模型在训练集上拟合,然后用拟合的模型来预测验证集的观测得响应变量。
(3).计算验证集的错误率,一般用均方误差。

-
下面我们用一个例子来说明这种方法:
在Auto数据集上,我们经过数据初步探索分析出来:mpg(因变量)和horsepower(自变量)之间似乎存在非线性关系,而我们应该使用多少次多项式拟合mpg与horsepower 之间的关系比较合适呢?下面我们使用验证集方法(validation set approach)来解决这个问题:
(1).我们 随机 将392个观测分为两个集合,一个包含196个数据点的训练集,一个包含剩余196个数据点的验证集。
(2).我们用包含196个数据点的训练集拟合多项式次数1-10的回归模型。
(3).对这10个中的每个模型,我们用包含剩余196个数据点的测试集来预测每个模型的均方误差(Mean Squared Error)。
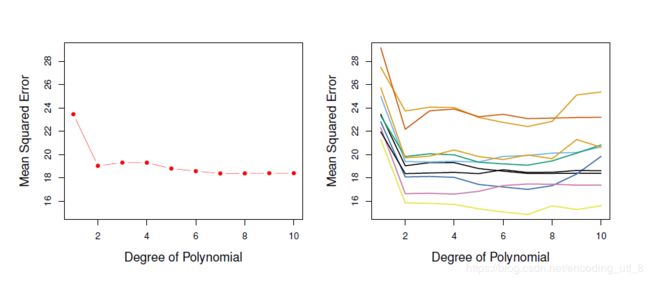
(4).将每个次数的多项式模型的均方误差的点画在图上(下图左图每个红色点代表每个多项式的均方误差)通过图像,我们发现基于验证集的二次项拟合的均方误差比线性模型小的多,而用三次项拟合回归模型并不比只用二次项拟合的模型好,这就验证了我们上图中一般模型的训练误差及测试误差与模型复杂度的关系,增加模型复杂度不一定减少测试集的误差率。
-
下面我们来评价验证集方法(validation set approach)的优缺点:
我们把验证集方法(validation set approach)的步骤(1)重复10次,即执行10种不同的抽样,然后每种抽样都执行验证集方法(validation set approach)的步骤(2)~(4),我们得出了上图的右图的10条不同的折线,10条折线都说明了用二次项拟合的模型比线性模型的验证集均方误差小得多,也说明了用三次或者更高次项拟合模型的效果并没有显著提升。(但是这些折线并不能说明哪个模型有最小的验证集均方误差,基于这些折线的波动性,只能确定这个数据做线性拟合不合适!)
验证集方法的原理很简单,且易于执行,蛋挞有两个潜在缺陷:
(1).正如上图右图所示,测试错误率的验证集方法估计的波动很大,这取决于具体哪些观测被包括在训练集中,哪些观测被包含在验证集中。
(2).在验证集方法中,我们仅使用了全体数据的一部分(训练集)去拟合模型,由于被训练的观测越少,统计方法的效果就越不好,这意味着验证集错误率可能 高估了在整个数据集上拟合所得到的的模型所得到的测试错误率。 -
针对以上验证集方法(validation set approach)的两个缺陷,我们使用了改进的方法:交叉验证法(cross validation)。
5.1.2 留一交叉验证法(leave-one-out cross-validation,LOOCV)
-
留一交叉验证法(leave-one-out cross-validation,LOOCV)的步骤:
(1).假设全体样本为 { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . . . . , ( x n , y n ) } {\{(x_1,y_1),(x_2,y_2),......,(x_n,y_n)\}} {(x1,y1),(x2,y2),......,(xn,yn)} 共n个样本,取其中的 ( x i , y i ) {(x_i,y_i)} (xi,yi)作为验证集,其余n-1个样本的作为训练集。
(2).将n-1个样本拟合模型,然后用拟合的模型来预测 ( x i , y i ) {(x_i,y_i)} (xi,yi)得响应变量,并计算均方误差 M S E i {MSE_i} MSEi。
(3).将上述步骤(1)(2)重复n次,也就是每个点都成为了一次验证集最后计算n个测试误差的均值: C V ( n ) = 1 n ∑ i = 1 n M S E i {CV_{(n)}=\frac{1}{n}\sum\limits_{i=1}^nMSE_i} CV(n)=n1i=1∑nMSEi。
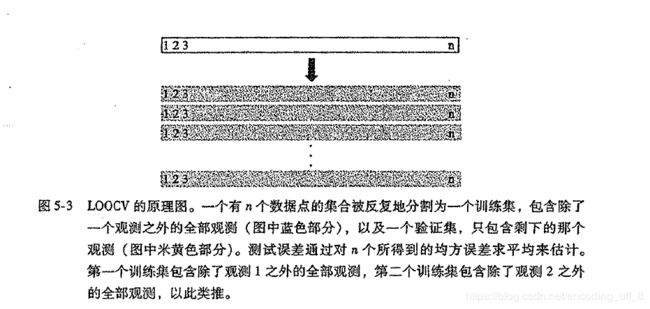
-
下面我们来举个例子使用这个方法:
我们使用LOOCV方法对Auto数据集上的mpg和horsepower的1-10次多项式拟合模型,得到下左图,由于LOOCV对取样没有随机性,我们无法像验证集方法上对随机抽取的样本建模然后绘制10条折线:(对比验证集方法上的图,有什么异同?)

-
LOOCV方法的优点(与验证集方法对比):
(1).相对于验证集方法,LOOCV 的方法的偏差(bias)较少,因为他几乎使用了所有的样本去拟合数据,所以这个方法提供了对于测试误差的一个渐进无偏估计: lim n → ∞ E ( C V ( n ) ) = t e s t e r r o r \lim\limits_{n\to\infty}E(CV_{(n)}) = test \;error n→∞limE(CV(n))=testerror(真实值)。因此LOOCV方法比验证集方法更不容易高估测试错误率。
(2).由于LOOCV方法在训练集和验证集的分割不存在随机性,所以反复运用LOOCV方法总会得到相同的结果 C V ( n ) {CV_{(n)}} CV(n)。 -
LOOCV方法的缺点(与验证集方法对比):
LOOCV方法 的计算量可能很大,因为模型需要被拟合n次,如果n很大或者模型拟合起来很慢的话,这种方法很耗时。但是,当应用最小二乘法去拟合模型时候,LOOCV方法所花费的时间还会神奇的缩减为拟合一个模型相同: C V ( n ) = 1 n ∑ i = 1 n ( y i − y ^ i 1 − h i ) 2 {CV_{(n)} = \frac{1}{n}\sum\limits_{i=1}^n(\dfrac{y_i-\hat{y}_i}{1-h_i})^2} CV(n)=n1i=1∑n(1−hiyi−y^i)2,其中 h i = 1 n + ( x i − x ˉ ) 2 ∑ i = 1 n ( x i ′ − x ˉ ) 2 {h_i=\frac{1}{n}+\dfrac{(x_i-\bar{x})^2}{\sum\limits_{i=1}^n(x_{i^{'}}-\bar{x})^2}} hi=n1+i=1∑n(xi′−xˉ)2(xi−xˉ)2 ( h i h_i hi在线性回归中被称为杠杆值)。 -
由于LOOCV方法在n很大时,这种方法会非常耗时,因此K折交叉验证(k-fold CV是LOOCV方法的一种替代。
5.1.3 K折交叉验证(k-fold CV)
- K折交叉验证(k-fold CV)的步骤:
(1).将观测集随机分成k个大小基本一样的组(折),将第一折作为验证集(保留集),其余k-1折作为拟合模型。
(2).使用保留集计算均方误差 M S E 1 MSE_1 MSE1。
(3).重复步骤(1)(2)k次,将k个MSE取平均值:
即: C V ( k ) = 1 k ∑ i = 1 k M S E i \;\;\;\;\;CV_{(k)}=\frac{1}{k}\sum\limits_{i=1}^{k}MSE_i CV(k)=k1i=1∑kMSEi
(下图为k折CV方法的每一次重复的原理)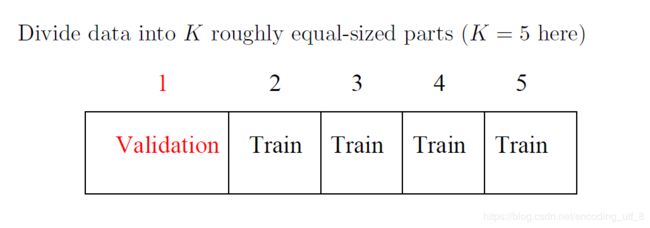
- K折交叉验证(k-fold CV)的优点(与LOOCV方法比较):
不难发现,当k=n时,LOOCV方法是k折交叉验证(k-fold CV)的一个特例。在实践中,使用k折CV方法时,一般令**k=5或k=10**而不是k=n的优势在哪呢?
(1).最显著的优势在于:计算方便。
LOOCV方法需要对一种统计学习方法拟合n次,它的计算量可能很大(除了最小二乘方法可以用公式算出来外);但是用10折交叉验证,只需要对这个统计方法拟合10次,可行性更高。
(2).在完成 模型评价(model assessment) 和 模型选择(model selection) 这两个目的上效果相差不是很大,甚至更加优秀(涉及偏差-方差权衡的问题,在下部分详细阐述)。


在上图中,蓝色实线测试均方误差真值,黑色虚线和橙色实线分别代表LOOCV方法和10折CV方法估计。在三个图中,两种交叉验证都比较接近。图5-6右边部分,测试均方误差的真值与交叉验证估计几乎重合了。在图5-6中间部分,在模型复杂度(光滑度)较低时,两条曲线比较接近,而当模型光滑度较高时,CV方法则高估了测试集均方误差。图5-6左边则CV曲线的形状大致正确,但都低估了均方误差的真值。
使用交叉验证法时,我们更希望的有时候不是得到某种统计学习方法的最小均方误差的值是多少,而是最小均方误差下对应的模型复杂度,也就是选出一个合适的模型使得均方误差最小。处于这个目的,我们来看看这三个图,尽管CV方法有时候会低估测试均方误差的真值,但所有的CV曲线都非常接近于确认的正确光滑度水平的模型,即真实最小测试均方误差最小值对应的模型复杂度。
- K折交叉验证(k-fold CV)的优点(与LOOCV方法比较):
5.1.4 k折交叉验证的偏差-方差权衡
- 在上一节中我们说到了当k
偏差-方差权衡的问题了。
(1).在LOOCV方法上,LOOCV方法在n-1个观测点上进行训练,这个数据量相当于整个数据集中观测的数目,这样LOOCV方法能提供接近无偏的测试误差估计,也就是当样本数n足够大时,测试误差的均值会接近于真实值。从减少偏差的角度来说,LOOCV方法的确比k折CV方法好很多。但仅仅考虑无偏性足够了吗,还得考虑结果的方差。
(2).当kσ 2 {\sigma^2} σ2(不一定是这个数,只是简单拿来比较结果的)。相反,在k折CV方法上,每个模型的训练集之间重合的部分相对较少,因此是在平均k个相关性较少的拟合模型的结果,综合起来它的方差大致上是 σ 2 / n {\sigma^2/n} σ2/n。由于许多高度相关的量的均值要比不相关的量的均值具有更高波动性,因此使用LOOCV方法所产生的的测试误差估计的方差要比k折CV方法所产生的的测试误差估计的方差大。 - 综上所述,在选择k折交叉验证的折数k时,涉及偏差-方差的权衡问题,这就是为什么k折交叉验证的k一般去k=10或者k=5的原因了,理由是这些值使得测试错误率的估计不会有过大的偏差和方差。
5.1.5 交叉验证法在分类问题的应用
- 至此,我们已经探讨了很多关于关于回归的问题,现在我们来说说分类问题与交叉验证的用法。分类问题与回归问题的区在交叉验证的区别在于测试误差的指标不一样罢了:例如在LOOCV方法上的错误率的形式为: 1 n ∑ i = 1 n E r r i {\frac{1}{n}\sum_{i=1}^nErr_i} n1∑i=1nErri ,其中 E r r i = I ( y i ≠ y ^ i ) {Err_i = I(y_i \ne \hat{y}_i)} Erri=I(yi=y^i),当k折时也一样的类似定义。
5.2 自助法(bootstrap)
- 自助法(bootstrap) 是一个广泛应用且非常强大的统计工具,可以用它来衡量一个指定的估计量或统计学习方法的不确定因素。举个例子:自助法可以用来估计线性回归模型的拟合系数的标准误差。
- 下面我们来用一个例子来说明自助法(bootstrap)的原理及优势:
假设希望用一笔固定数额的钱对两个收益率为X和Y 的金融资产进行投资,其中X和Y为随机变量。打算把所有钱的百分比 α \alpha α部分投资到X,把剩下的 1 − α 1-\alpha 1−α部分投资到Y。由于入市有风险,投资需谨慎,我们应该选择一个合理的 α \alpha α使得投资的总风险及方差最小,换句话说,我们希望得到一个 α \alpha α使得 V a r ( α X + ( 1 − α ) Y ) {Var(\alpha X+(1-\alpha)Y)} Var(αX+(1−α)Y)最小。现在我们通过数学推导,得到了最优的 α \alpha α, α = σ Y 2 − σ X Y σ X 2 + σ Y 2 − 2 σ X Y {\alpha = \dfrac{\sigma_Y^2-\sigma_{XY}}{\sigma_X^2+\sigma_Y^2-2\sigma_{XY}}} α=σX2+σY2−2σXYσY2−σXY,
其中 σ X 2 = V a r ( X ) , σ Y 2 = V a r ( Y ) , σ X Y = c o v ( X , Y ) {\sigma_X^2=Var(X),\sigma_Y^2=Var(Y),\sigma_{XY}=cov(X,Y)} σX2=Var(X),σY2=Var(Y),σXY=cov(X,Y)
在现实中,我们的 σ X 2 , σ Y 2 , σ X Y {\sigma_X^2,\sigma_Y^2,\sigma_{XY}} σX2,σY2,σXY都是未知的,我们需要找到很多历史数据对他们进行估计,下图展示了一个模拟数据集上用这个方法来估计 α \alpha α的结果。模拟器生成了100对投资的X,Y。用这些收益来估计 σ X 2 , σ Y 2 , σ X Y {\sigma_X^2,\sigma_Y^2,\sigma_{XY}} σX2,σY2,σXY,然后代入公式 α = σ Y 2 − σ X Y σ X 2 + σ Y 2 − 2 σ X Y {\alpha=\dfrac{\sigma_Y^2-\sigma_{XY}}{\sigma_X^2+\sigma_Y^2-2\sigma_{XY}}} α=σX2+σY2−2σXYσY2−σXY,得到了 α \alpha α的很多估计。
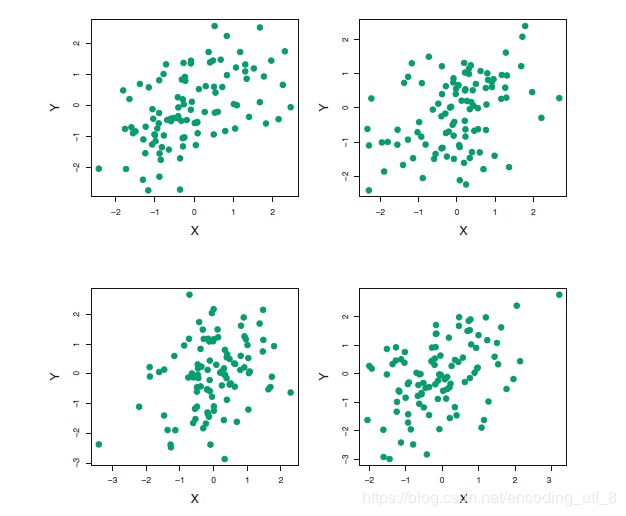

下面我们希望评估下 α \alpha α估计的精度。为了估计 α ^ {\hat{\alpha}} α^的标准差,我们重复模拟生成了100对X和Y的观测,然后用 α = σ Y 2 − σ X Y σ X 2 + σ Y 2 − 2 σ X Y {\alpha=\dfrac{\sigma_Y^2-\sigma_{XY}}{\sigma_X^2+\sigma_Y^2-2\sigma_{XY}}} α=σX2+σY2−2σXYσY2−σXY来估计 α \alpha α,这一步骤重复1000次,因此得到了1000个 α \alpha α的估计,记为 α 1 ^ , α 2 ^ , . . . . . . , α ^ 1000 {\hat{\alpha_1},\hat{\alpha_2},......,\hat{\alpha}_{1000}} α1^,α2^,......,α^1000。下图左图展示了所得估计的直方图。在模拟数据的时候,我们的模拟器假设真实的 α = 0.6 \alpha=0.6 α=0.6,在直方图中用一条垂直的实线标注了出来。因此,1000个估计的 α \alpha α的均值为: α ˉ = 1 1000 ∑ r = 1 1000 α r ^ = 0.5996 {\bar{\alpha} = \frac{1}{1000}\sum\limits_{r=1}^{1000}\hat{\alpha_r} = 0.5996} αˉ=10001r=1∑1000αr^=0.5996,这与真实的 α = 0.6 \alpha=0.6 α=0.6很接近了,而估计量的方差为 S E ( α ^ ) = 1 1000 − 1 ∑ r = 1 1000 ( α ^ r − α ˉ ) 2 = 0.083 {SE(\hat{\alpha})=\sqrt{\frac{1}{1000-1}\sum\limits_{r=1}^{1000}(\hat{\alpha}_r-\bar{\alpha})^2} =0.083} SE(α^)=1000−11r=1∑1000(α^r−αˉ)2=0.083,所以大致上说对于总体的一个随机样本,可以认为平均上 α ^ {\hat{\alpha}} α^跟 α {\alpha} α的差距大致为0.083。


但是在实际中,我们不可能对同一个样本总体生成如此多的样本去估计你想要的统计量的精度,因为我们不可能在实际中不断地去投资去实验得到那么多的样本(除非你真的氪金得到了)。不过,自助法(bootstrap)能够帮你实现这个愿望。相比于从总体中反复地得到独立的数据集,自助法通过反复地从原始数据集中抽取观测得到数据集(放回抽样)。
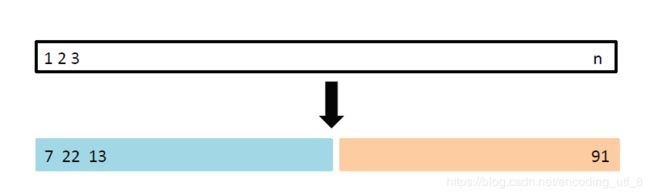
我们说明下自助法的实现过程:
(1).首先从数据集中选择n个观测,选择的过程是有放回抽样,产生一个自助法数据集 Z ∗ 1 {Z^{*1}} Z∗1。(意味着同一个 Z ∗ 1 {Z^{*1}} Z∗1中可能存在相同的观测)
(2).重复过程(1)产生B个 Z ∗ i {Z^{*i}} Z∗i
(下图说明自助法的原理)
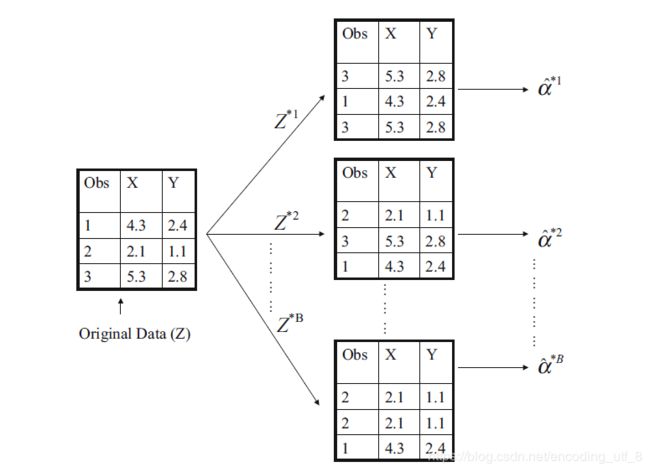

因此,我们在每个自助法数据集 Z ∗ i {Z^{*i}} Z∗i上得到相应的 α ^ i ∗ i {\hat{\alpha}_i^{*i}} α^i∗i,计算得到 S E ( α ^ ) = 1 B − 1 ∑ r = 1 B ( α ^ r − α ˉ ) 2 {SE(\hat{\alpha})=\sqrt{\frac{1}{B-1}\sum\limits_{r=1}^{B}(\hat{\alpha}_r-\bar{\alpha})^2}} SE(α^)=B−11r=1∑B(α^r−αˉ)2
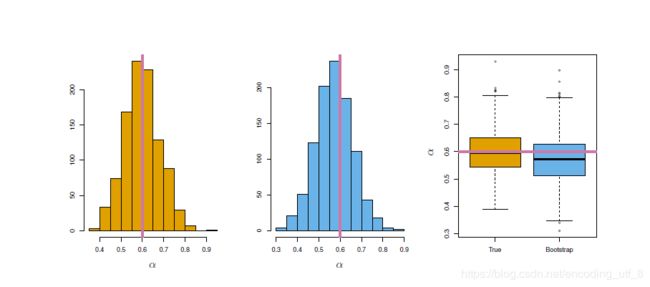

上图中间部分展示了1000个 α {\alpha} α的自助法估计的直方图,与左图的真实数据模拟的理想直方图很相似,且自助法计算 S E ( α ^ ) = 1 B − 1 ∑ r = 1 B ( α ^ r − α ˉ ) 2 = 0.087 {SE(\hat{\alpha})=\sqrt{\frac{1}{B-1}\sum\limits_{r=1}^{B}(\hat{\alpha}_r-\bar{\alpha})^2}=0.087} SE(α^)=B−11r=1∑B(α^r−αˉ)2=0.087,和模拟数据及中的0.083非常的接近,这表明自助法能有效的估计涉及 α ^ {\hat{\alpha}} α^的波动性。
5.3 具体代码实现(R语言版本)
5.3.1验证集方法
我们将使用Auto数据集进行演示:
library(ISLR)
library(RColorBrewer)
miscolores = brewer.pal(8,"Set2")[1:8]
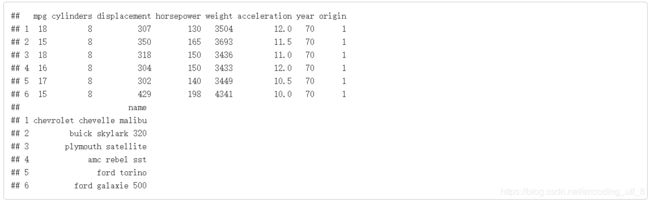
head(Auto)
attach(Auto)
par(mar = c(5, 5, 0.1, 0.1))
plot(horsepower, mpg, pch = 12, col = miscolores[5], xlab = "Horsepower", ylab = "mpg")
detach()
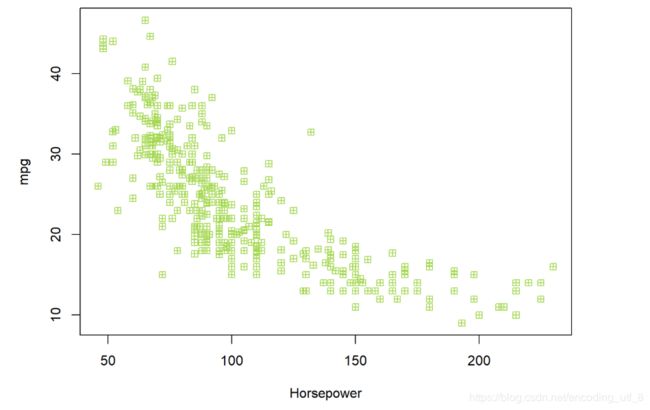
首先,我们使用函数sample()把数据分成不相交的两部分,函数sample()可以得到随机样本。第一个参数一般是一个向量,函数sample()的返回值随机的在这个向量中抽取,在我们的例子中,该向量是1到n的自然数;第二个参数表示要抽取的随机数的个数,在这里,我们将用200个观测点组成的数据作为训练数据;第三个参数表示是否是有放回的抽取。因此,在上面的例子中,函数sample()的结果是一个向量,该向量有200个元素,这200个元素是从1到n这些自然数等概率的抽取出来的。而且这200元素全都是不一样的,因为我们设置replace=F,是没有放回的抽取。
set.seed(1)
n <- nrow(Auto) # "nrow()"得到数据框行的个数
train <- sample(1:n, 200, replace = F)
length(train)
train[1:10]

接着,我们使用包含在train里面的观测点建立线性回归模型,然后使用不在train里的观测点计算预测误差,
lm.fit <- lm(mpg ~ horsepower, data = Auto, subset = train)
mean((Auto$mpg[-train] - predict(lm.fit, Auto)[-train])^2)
我们可以再做一次类似的实验,使用不同的随机数,那么划分到训练集和测试集的观测点将会不一样,
set.seed(2)
train <- sample(1:n, 200, replace = F)
lm.fit <- lm(mpg ~ horsepower, data = Auto, subset = train)
mean((Auto$mpg[-train] - predict(lm.fit, Auto)[-train])^2)
我们可以试试用同样的方式,得到100个预测误差,
err <- rep(0, 100)
for (i in 1:100) {
+ train <- sample(1:n, 200, replace = F)
+ lm.fit <- lm(mpg ~ horsepower, data = Auto, subset = train)
+ err[i] <- mean((Auto$mpg[-train] - predict(lm.fit, Auto)[-train])^2)
+ }
length(err)
err[1:10]
summary(err)
par(mfrow = c(1, 2), mar = c(5,5,0.1,0.1))
hist(err, col = miscolores[1], xlab = "Prediction Error", main = "")
boxplot(err, col = miscolores[2], ylab = "Prediction Error")
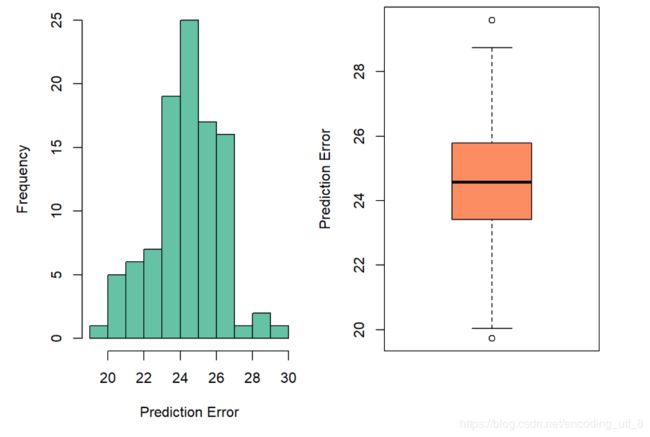
我们重复了100次实验,最小的预测误差为19.7312618, 最大的预测误差为29.5977063。在这个数据中,我们以mpg为因变量,以horsepower为自变量建立的线性模型的预测误差的平均值是24.4187267。 可以看到,不同实验得到的结果差别是很大的。
5.3.2 k-fold CV方法
从上面的分析,我们可以看到validation method估计的预测误差稳定性不太好,k-fold CV可以有效的降低这种不稳定性,提供一个更好的预测误差的估计。在CV中, 我们随机的把数据分成k份,然后把第一份数据当成是测试数据,其他的数据作为训练数据;接着把第二份数据看成是测试数据,其他的数据作为训练数据;以此类推。 我们依然使用函数sample()实现上述目的,
nfolds <- 2
tmp <- rep(1:nfolds, length = n)
length(tmp)
tmp[1:25]
index <- sample(tmp, n, replace = F)
index[1:25]
table(index)
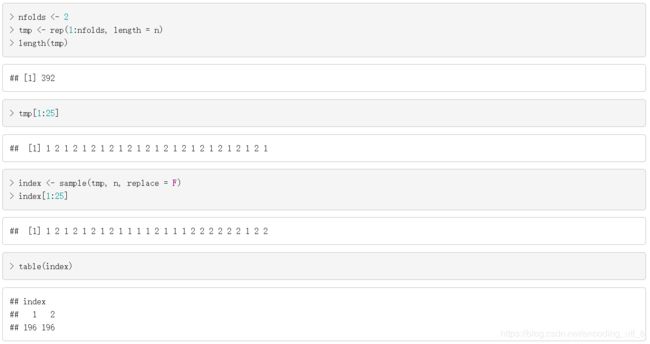
首先我们先得到一个向量tmp, 重复列出1到nfolds的自然数,总的长度是数据的行数n。然后再使用函数sample(),无放回,等概率的从tmp中抽取n个数。这时sample()的效果就是把tmp的数打乱。我们可以看看函数sample()得到的结果index。index中只包含了nfolds个不同的数,这时我们可以把所有“1”对应的观测值看成第一组,所有“2”对应的观测值看成第二组… 这样就实现了随机的对数据进行分组。接着,使用for循环实现CV,
nfolds <- 2
mse <- rep(0, nfolds)
index <- sample(rep(1:nfolds, length = n), n, replace = F)
for(i in 1:nfolds) {
+ train <- which(index != i)
+ lm.fit <- lm(mpg ~ horsepower, data = Auto, subset = train)
+ mse[i] <- mean((Auto$mpg[-train] - predict(lm.fit, Auto)[-train])^2)
+}
cv_value <- mean(mse)
cv_value

为了描述上更加简单,在这里我们先设定nfolds=2。我们先产生一个随机的向量index, 该向量包含了1到nfolds的自然数。 然后使用for循环, i先等于1, index != i判断那些index里的元素不等于1,得到的是一个逻辑向量,然后函数which()可以得到index中哪些元素是不等于1的, 接着我们用train里面的元素所对应的观测点建立回归模型,最后使用不在train里面的观测点计算预测误差,完成第一次循环;第二次循环时,i等于2,函数which()可以得到index中哪些元素是不等于2的, 接着我们用train里面的元素所对应的观测点建立回归模型,最后使用不在train里面的观测点计算预测误差。最后,我们求2次预测的平均值,即我们要得到的CV值。
我们也可以把CV的过程写进一个函数中,方便以后使用,我们自定义了一个函数cv_fun计算线性回归模型的CV值。函数cv_fun有两个参数,第一个参数是数据,第二个参数k表示把数据分成的份数。这时我们还给参数k设定了默认值,10。使用函数cv_fun时,如果我们没有明确的给k设定一个量,k就等于它的默认值10。函数的最后没有写明return时,默认返回写在函数内部的最后一个对象,在这个例子,返回的是cv_value。 例如,
cv_fun <- function(dat, k = 10) {
+
+ n <- nrow(dat)
+ index <- sample(rep(1:k, length = n), n, replace = F)
+
+ mse <- rep(0, k)
+ for(i in 1:k) {
+ train <- which(index != i)
+ lm.fit <- lm(mpg ~ horsepower, data = dat, subset = train)
+ mse[i] <- mean((dat$mpg[-train] - predict(lm.fit, dat)[-train])^2)
+ }
+ cv_value <- mean(mse)
+ cv_value
+ }
cv_fun(dat = Auto, k = 2)
cv_fun(dat = Auto) # 这时 k = 10

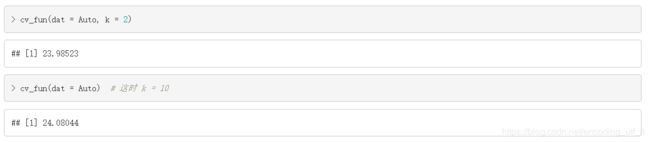
我们还可以考虑建立一个多项式模型,以mpg作为因变量,horsepower和horsepower2作为自变量,用CV估计模型的预测误差,我们自定义了一个函数cv_fun_poly(), 和函数cv_fun()唯一的区别在使用函数lm()时,公式mpg ~ horsepower改成了函数cv_fun_poly()里的 mpg ~ horsepower + I(horsepower2)。I(horsepower2)表示horsepower的平方项。
cv_fun_poly <- function(dat, k = 10) {
+
+ n <- nrow(dat)
+ index <- sample(rep(1:k, length = n), n, replace = F)
+
+ mse <- rep(0, k)
+ for(i in 1:k) {
+ train <- which(index != i)
+ lm.fit <- lm(mpg ~ horsepower + I(horsepower^2), data = dat, subset = train)
+ mse[i] <- mean((dat$mpg[-train] - predict(lm.fit, dat)[-train])^2)
+ }
+ cv_value <- mean(mse)
+ cv_value
+ }
cv_fun_poly(dat = Auto, k = 5)
cv_fun_poly(dat = Auto) # 这时 k = 10

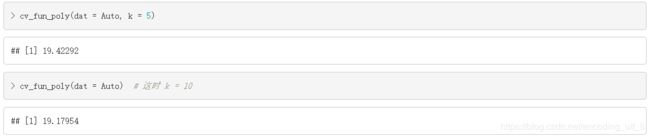
可以看到,加了二次项的模型的预测误差大概等于20, 而只有一次项的模型的预测误差约等于25。根据这两个模型的预测误差,我们可以选择预测误差小的模型,即加了二次项的线性回归模型。
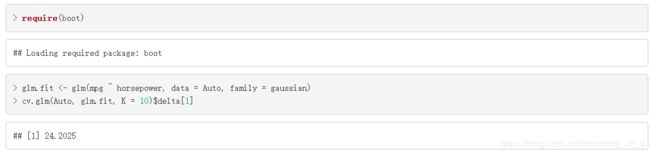
在R中,我们也可以使用函数cv.glm()计算广义线性模型的CV值,函数glm()也可以用来拟合线性回归模型,这时需把参数family=gaussian。然后再使用包boot里的函数cv.glm()得到CV值。函数cv.glm()的第一个参数是数据,第二个参数是拟合的线性回归模型,第三个参数是CV分组的个数。
require(boot)
glm.fit <- glm(mpg ~ horsepower, data = Auto, family = gaussian)
cv.glm(Auto, glm.fit, K = 10)$delta[1]
5.3.3 Bootstrap
我们使用数据Portfolio学习如何实现bootstrap计算估计量的方差。数据Portfolio在包ISLR内。数据Portfolio有两个投资品种,X和Y的100天的收益率。
require(ISLR)
head(Portfolio)
dim(Portfolio)
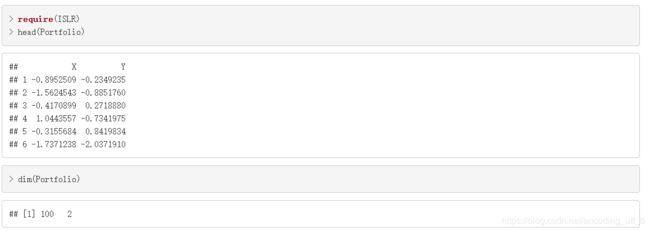
我们的目的是计算资金分配到X和Y的比例,α。可以通过最小化投资组合的方差得到,即 m i n α = V a r ( α X + ( 1 − α ) Y ) {min_{\alpha} = Var(\alpha X+(1-\alpha)Y)} minα=Var(αX+(1−α)Y),通过对 V a r ( α X + ( 1 − α ) Y ) {Var(\alpha X+(1-\alpha)Y)} Var(αX+(1−α)Y)求导数,可以得到α的估计值: α = σ Y 2 − σ X Y σ X 2 + σ Y 2 − 2 σ X Y {\alpha = \dfrac{\sigma_Y^2-\sigma_{XY}}{\sigma_X^2+\sigma_Y^2-2\sigma_{XY}}} α=σX2+σY2−2σXYσY2−σXY
X <- Portfolio$X
Y <- Portfolio$Y
alpha <- (var(Y) - cov(X, Y)) / (var(X) + var(Y) - 2*cov(X, Y))
alpha
Boostrap产生大量bootstrap样本,然后计算每个bootstrap样本下,α的估计值,最后再根据这些bootstrap样本的估计值,计算α的估计值的标准差。我们可以使用函数sample()得到bootstrap样本,
n <- nrow(Portfolio)
idx <- sample(1:n, n, replace = T)
length(idx)
idx[1:15]
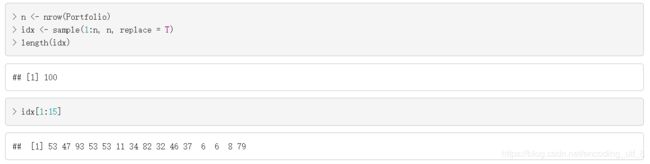
我们通过有放回的抽取得到bootstrap样本,所以把函数sample()的参数replace设成了TRUE。 bootstrap样本的观测点数量和原数据是一样的。
X_boot <- X[idx]
Y_boot <- Y[idx]
alpha_boot <- (var(Y_boot) - cov(X_boot, Y_boot)) / (var(X_boot) + var(Y_boot) - 2*cov(X_boot, Y_boot))
bootstrap样本即(X_boot, Y_boot), 然后计算这个样本下的投资分配比例,alpha_boot。把上述的代码整理,放到for循环中,
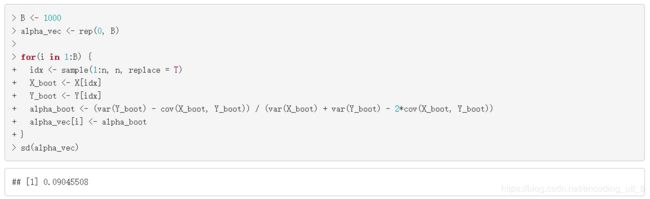
B <- 1000
alpha_vec <- rep(0, B)
for(i in 1:B) {
+ idx <- sample(1:n, n, replace = T)
+ X_boot <- X[idx]
+ Y_boot <- Y[idx]
+ alpha_boot <- (var(Y_boot) - cov(X_boot, Y_boot)) / (var(X_boot) + var(Y_boot) - 2*cov(X_boot, Y_boot))
+ alpha_vec[i] <- alpha_boot
+ }
sd(alpha_vec)
par(mar = c(5,5,0.1,0.1))
hist(alpha_vec, col = miscolores[2], xlab = expression(alpha), main = "")

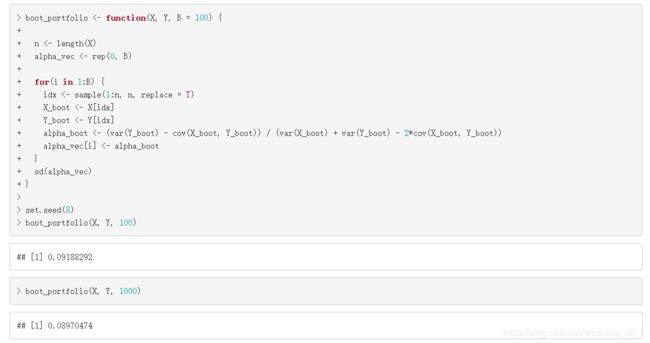
因此,α^的bootstrap估计是0.0904551。上面代码中,B表示的是bootstrap样本的个数。我们也可以上面的代码放在函数中,方便之后使用,
boot_portfolio <- function(X, Y, B = 100) {
+
+ n <- length(X)
+ alpha_vec <- rep(0, B)
+
+ for(i in 1:B) {
+ idx <- sample(1:n, n, replace = T)
+ X_boot <- X[idx]
+ Y_boot <- Y[idx]
+ alpha_boot <- (var(Y_boot) - cov(X_boot, Y_boot)) / (var(X_boot) + var(Y_boot) - 2*cov(X_boot, Y_boot))
+ alpha_vec[i] <- alpha_boot
+ }
+ sd(alpha_vec)
+ }
set.seed(8)
boot_portfolio(X, Y, 100)
boot_portfolio(X, Y, 1000)
R的包boot中有函数boot()也可以帮助我们实现boottrap。使用函数boot()之前,我们先做一些准备,
函数alpha_fn()主要的功能是计算α的估计值,只是alpha_fn()可以通过改变参数index, 实现改变计算bootstrap样本的α。如果index = 1:n, 那么data X [ i n d e x ] 和 d a t a X[index]和data X[index]和dataY[index]就是原数据的data X 和 d a t a X和data X和dataY。这时得到的就是原数据的α估计值。
alpha_fn <- function(data, index) {
+ X <- data$X[index]
+ Y <- data$Y[index]
+ return((var(Y) - cov(X, Y)) / (var(X) + var(Y) - 2*cov(X, Y)))
+ }
lpha_fn(Portfolio, index = 1:100)

如果index表示的是从1:n等可能有放回抽取的长度为n的向量,那么data X [ i n d e x ] 和 d a t a X[index]和data X[index]和dataY[index]是一个bootstrap样本。这时函数alpha_fn()返回的结果就是一次bootstrap样本的α估计值。
idx <- sample(1:100, 100, replace = T)
alpha_fn(Portfolio, index = idx)

现在我们可以使用函数boot()实现bootstrap, 不需要自己使用for循环:
set.seed(123)
boot(Portfolio, alpha_fn, R = 1000)
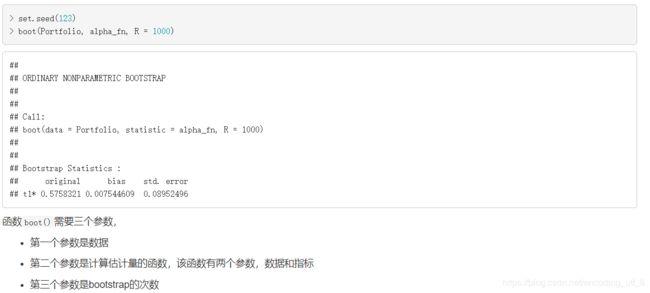
通过这个方法得到的α的估计的标准差是0.0875, 而通过我们自己写的函数boot_portfolio()计算的标准差是0.091(bootstrap的次数是1000时),两者是比较接近的。
5.4 结语:
通过本章的学习,我们知道了在现实的数据挖掘中,我们怎么去评价一个模型的好坏,或者选择更好的模型的方法,包括验证集方法,留一法,k折交叉验证法,自助法。那在下一章中,我们就来解决本章开头没有解决的问题:通过数学修正Cp , AIC ,BIC等将训练错误率修正估计训练错误率,以及如何在选定模型后选择合适的特征建模,包括子集选择,压缩估计和降维。
参考文献
[1]加雷斯.詹姆斯,丹妮拉.威腾 .统计学习导论[M].北京:机械工业出版社,2015.6.
[2]李航.统计学习方法[M].北京:清华大学出版社,2012.3.
[3]杰克.万托布拉斯.Python数据科学手册[M].北京:人民邮电出版社,2018.2.
[4]富朗索瓦.肖莱.Python深度学习[M].北京:人民邮电出版社,2018.8