树的直径

【定义】

我们将一棵树T = ( V，E )的直径定义为maxδ ( u，v ) ( u，v ∈ V )，也就是说，树中所有最短路径距离的最大值即为树的直径。

 

【做法】

例题传送门Cow Marathon（POJ 1985）

对于树的直径呢，我们老师给我们介绍了两种做法，一种是用两次bfs（或者dfs），另一种是用树形DP

 

1、两次bfs（或者dfs）

方法：先从任意一点P出发，找离它最远的点Q，再从点Q出发，找离它最远的点W，W到Q的距离就是是的直径

证明如下：

①若P已经在直径上，根据树的直径的定义可知Q也在直径上且为直径的一个端点

②若P不在直径上，我们用反证法，假设此时WQ不是直径，AB是直径

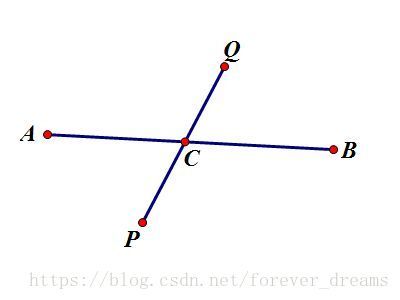
--->若AB与PQ有交点C，由于P到Q最远，那么PC+CQ>PC+CA，所以CQ>CA，易得CQ+CB>CA+CB，即CQ+CB>AB，与AB是直径矛盾，不成立，如下图（其中AB，PQ不一定是直线，画成直线是为了方便）：

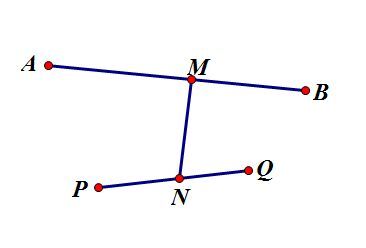
--->若AB与PQ没有交点，M为AB上任意一点，N为PQ上任意一点。首先还是NP+NQ>NQ+MN+MB，同时减掉NQ，得NP>MN+MB，易知NP+MN>MB，所以NP+MN+MA>MB+MA，即NP+MN+MA>AB，与AB是直径矛盾，所以这种情况也不成立，如下图：

代码（dfs）：

#include
#include
#include
using namespace std;
const int N=100005;
int n,m,t,p,ans;
int d[N],first[N],v[N],w[N],next[N];
void add(int x,int y,int z)
{
	t++;
	next[t]=first[x];
	first[x]=t;
	v[t]=y;
	w[t]=z;
}
void dfs(int x,int father)
{
	int i,j;
	if(ans

 

2、树形DP

对于每个节点我们要记录两个值：

f1 [ i ] 表示以 i 为根的子树中，i 到叶子结点距离的最大值

f2 [ i ] 表示以 i 为根的子树中，i 到叶子结点距离的次大值

对于一个节点，它到叶子结点距离的最大值和次大致所经过的路径肯定是不一样的

若j是i的儿子，那么（下面的 w [ i ][ j ] 表示 i 到 j 的路径长度）：

1. 若 f1 [ i ] < f1 [ j ] + w [ i ][ j ]，f2 [ i ] = f1 [ i ]，f1 [ i ] = f1 [ j ] + w [ i ][ j ]；
2. 否则，若 f2 [ i ] < f1 [ j ] + w [ i ][ j ]，f2 [ i ] = f1 [ j ] + w [ i ][ j ]； 

理解：这样做就是，先看能否更新最大值，若能，它的次大值就是原先的最大值，再更新它的最大值；若不能，就看能不能更新次大值，若能，就更新，不能就不管它

这样的话，最后的答案 answer = max { f1 [ i ] + f2 [ i ] }

代码（这是从叶节点到根节点的DP）：

#include
#include
#include
using namespace std;
const int N=100005;
int n,m,t,ans;
int f1[N],f2[N];
int first[N],v[N],w[N],next[N];
void add(int x,int y,int z)
{
	t++;
	next[t]=first[x];
	first[x]=t;
	v[t]=y;
	w[t]=z;
}
void dp(int x,int father)
{
	int i,j;
	for(i=first[x];i;i=next[i])
	{
		j=v[i];
		if(j==father)
		  continue;
		dp(j,x);
		if(f1[x]