斯坦福cs231n学习笔记(8)------神经网络训练细节(数据预处理、权重初始化)
神经网络训练细节系列笔记:
- 神经网络训练细节(激活函数)
- 神经网络训练细节(Batch Normalization)
- 神经网络训练细节(训练过程,超参数优化)
这一篇,我们将继续介绍神经网络训练细节。
一、Data Preprocessing(数据预处理)

如图是原始数据,数据矩阵X有三种常见的数据预处理形式,其中我们假定X的大小为[N×D](N是数据的数量,D是它们的维数)。
归一化处理(normalized data)
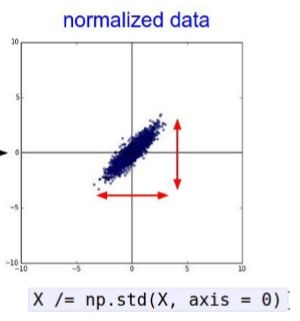
如上图所示,归一化处理是指每个维度都通过标准偏差来进行缩放或者确保每个维度最大值和最小值在-1到1之间等等,红线表示数据的范围,中间长度不等,右边长度相等。在图像处理中,归一化并不常用。零中心化处理
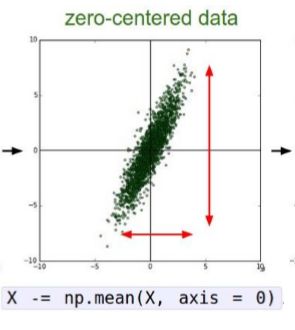
零中心化处理是指减去每个维度的平均值,进而使得数据是以零为中心的。数据云集中在原点的周围。在图像处理中,零中心化处理是一种常用的数据预处理的方式。PCA and Whitening(PCA算法和白化处理)
PCA和白化是数据预处理的另一种方式。在这个过程中,应用PCA算法将协方差矩阵变成对角矩阵,或者对数据进行白化处理,那意味着在PCA处理后对数据进行压缩,使协方差矩阵变成单位矩阵,这种预处理方式在机器学习中经常用到。
以上三种数据预处理的方法在图像处理中并不常用,在图像处理中常见的是均值中心化处理,以32*32*3的CIFAR图像为例,有两种方式实现:
减去均值图像
经过计算后得到一个32*32*3的均值图像,用每张图像减去均值图像进行中心化处理,从而获得更好的训练效果。
减去单通道均值
这种数据预处理方式常常用在VGGNet中,在红绿蓝三色通道中分别计算,分别得到3个数值。这种预处理方式非常常用,因为我们只需要关心三个数值,而不用考虑上一方法中均值图像中的那个均值图像数组。
二、Weight Initialization(权重初始化)
w(权重)的初始化问题也是早期神经网络发展不好的原因,是人们不重视的一个very very very重要的参数。首先,如果不进行初始化,那么在w=0的情况下所有的神经元都是一样的,在反向传播时的梯度都是一样的,这个网络是不能工作的,所有的神经元进行相同的计算,这不是一个很好的方式。因此,人们用很小的随机数值代替,随机数值是从标准差为0.01的高斯公式中随机抽取,这是w初始化的一种方式。

但是这种初始化方式是存在问题的,应用层数少的神经网络还可以,但是随着层数的增加,这种简单的初始化方法是无效的。下面将详细讲解什么方法无效以及Why,How。我们从代码、可视化数据来分析w的初始化过程。
D = np.random.randn[(1000,500)
hidden_layer_sizes = [500]*10
nornlinearities = ['tanh']*len(hidden_layer_sizes)我们要做的是用高斯分布来初始化权值w,然后进行网络传播,所以定义一个for循环,循环进行传播,即在一些相同尺寸的隐藏层中进行一系列计算。
act = {'relu':lambda x:np.maximum(0,x), 'tanh':lambda x:np.tanh(x)}
Hs = {}
for i in xrange(len(hidden_layer_sizes)):
X = D if i == 0 else Hs[i-1]
fan_in = X.shape[1]
fan_out = hidden_layer_sizes[i]
W = np.random.randn(fan_in,fan_out) * 0.01
H = np.dot(X,W)
H = act[nonlinearities[i]](H)
Hs[i] = HSo,我们希望更加了解隐藏层中的神经元会如何激活,因此我们着重关注均差和标准差,同时,我们将均差和标准差用柱状图绘制出来,让所有的数据通过网络,然后观察第五、第六或第七层上的权值,用柱状图显示出来。
print 'input layer had mean %f and std %f' % (np.mean(D), np.std(D))
layer_means = [np.mean(H) for i,H in Hs.iteritems()]
layer_stds = [np.std(H) for i,H in Hs.iteritems()]
for i,H in Hs.itemritems():
print ' hidden layer %d had mean %f and std %f' % (i+1, layer_means[i], layer_stds[i])
plt.figure()
plt.subplot(121)
plt.plot(Hs.keys(), layer_means, 'ob-')
plt.title('layer mean')
plt.subplot(122)
plt.plot(Hs.keys(), layer_means, 'or-')
plt.title('layer std')
plt.figure()
for i,H in Hs.iteritems():
plt.subplot(1,len(Hs),i+1)
plt.hist(H.ravel(),30,range=(-1,1))那么,我们采用标准差为0.01的高斯公式的策略初始化w:
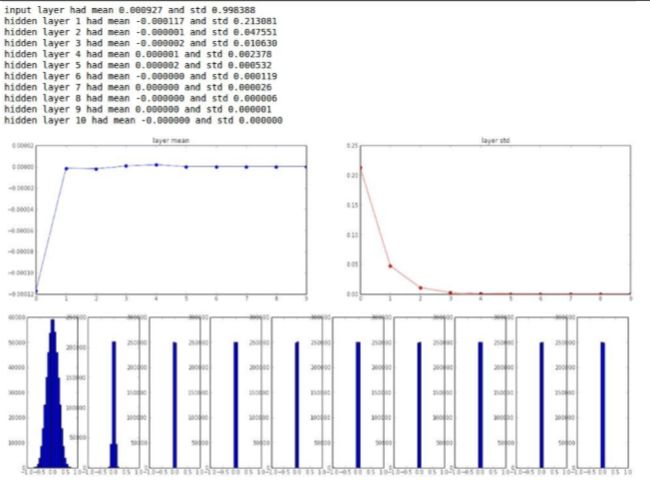
由图片中,我们可以看到,一开始输入的均值是0,标准差是1,在前向传播的过程中,我们观察经过10层网络之后的情况,我们使用的是tanh函数,tanh函数关于原点对称的,所以均值会归于0左右,再来看看方差,一开始是1,在接下来的层中,变成0.2,0.04,直线下降至0,所以神经元的方差会降到0。看柱状图,第一张是合理的,我们的数据处于-1到1之间,随后这些数据分布开始“坍塌”,最终只分布在0上,在10层网络上使用这种初始化方法,最终所有以tanh为激活函数的神经元,输出都是0,这是为什么?
A:输入X是小量数值,那么w的梯度也是小量数值,w*x的激活函数计算出的结果对梯度的叠加是无影响的,在反向传播过程中,通过链式法则不断的乘w,最终得到的梯度非常小,几乎为0,这时就出现了梯度弥散(消失)的问题。使用标准差为0.01的高斯分布策略进行w初始化,我们会发现梯度的量级不断缩小,所以我们可以尝试另一种方式来优化w初始化,与其将数值规整到-1和1之间,我们可以尝试一些其他的尺度来初始化w矩阵,*使用1.0来代替0.01。那么我们来看下此时的输出情况:
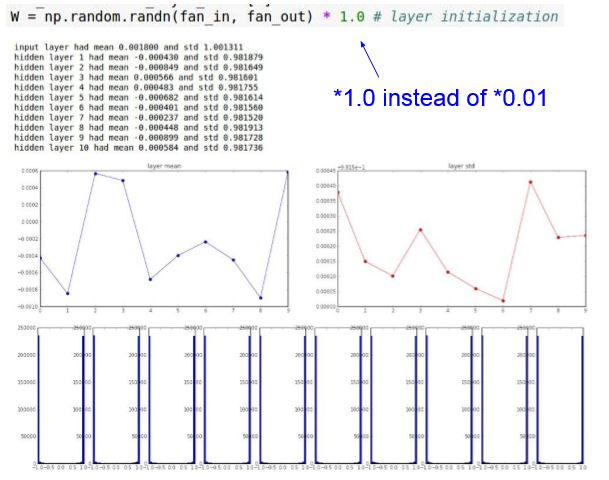
由图像可以看出,发生了另一个奇特的事情,因为我们“走过头”了。由于数值设置的过高,所有的tanh函数输出不是1就是-1,这意味着所有传递的数值都过于饱和了。因为w过大,正向传播后的数值就会变得非常大。那么在反向传播中计算的梯度就会趋向0,然后使得我们的网络无法工作,即使训练时间加长,损失函数也根本不会变,因为所有的神经元都饱和了,无法进行反向传播,权值得不到更新。基于此,我们没有必要在1.0和0.01之间进行手工测试。
2010年,有一篇是由Glorot等人写的论文,我们称之为Xavier初始化,他们关注了神经元的方差表达式,对每个神经元的输入进行开根号,如果有很多的输入,最终会得到较小的权值,从直观上来看,这么做是有意义的。
![]()
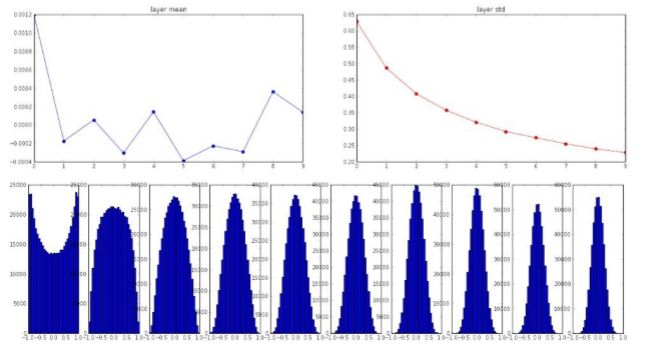
因为加权和中被算入的量更多了,而且希望它们之间的相关性降低。如果输入很少,那么我们需要较大的权值,因为其中仅有一小部分希望它们的方差是1。所以,这种思路的核心就是只关注单个神经元,不包括激活函数,仅仅是线性的神经元。如果我们输入的是高斯分布的数据,并且希望线性神经元方差是1,那么我们应该用这种方法对w进行初始化。从图像上看,数值的分布更有意义了 ,从-1到1之间的tanh单元的直方图,数值都在作用区域内,没有出现饱和的情况,这种方式效果也不是非常好,从一个直方图可以看出,出现了一个下凹,其原因是这篇论文并未考虑tanh的非线性。tanh函数的非线性,将数据的方差改变,这将影响数据方差的分布。So,这是一个靠谱的初始化方式,可以应用到神经网络中来,比起设置0.01要好得多。但是,虽然这种方法在tanh为激活函数的网络中奏效,但是换了ReLU,ReLU并不奏效,反而方差下降的更快,ReLU神经元分布越来越差,并趋于0,进而越来越多的神经元未被激活。
![]()
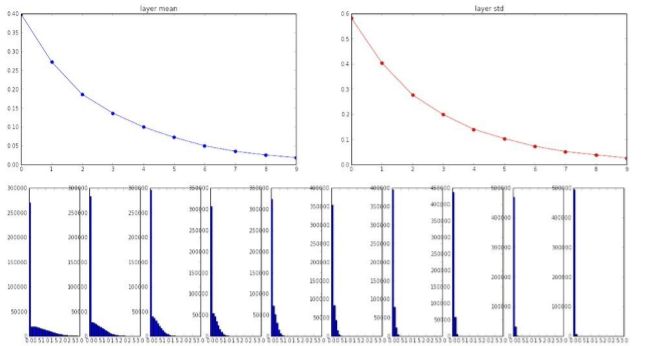
从ReLU的数据分布中,我们可以看到,在第一层中,能看出一些分布,但是在之后的几层中,分布越来越窄,并趋于0,也就说在这种初始化方法下,越来越多的神经元没有激活。所以这种初始化方式应用在ReLU网络中,并没有什么好的结果。回头看一下已tanh函数为激活函数的神经元,Glorot等人当年并没有讨论非线性和ReLU神经元的情况,所以在计算加权和后,让结果经过一个ReLU的激活函数,由ReLU神经元的数据分布可以看出,一半的贡献被置0了,从直观上来看,输出的分布是方差的一半。所以应用ReLU在高斯分布中应该额外考虑因数2,最终结果就会收敛;若没有引入因数2,激活函数输出的分布就会以指数倍收缩。如果你在实际中使用ReLU神经元,那么这里提到的这种初始化方法才是合理的。
In a word,w初始化问题在实际中是需要好好斟酌的,由于这是一种策略性的东西,所以才使得神经网络走这么远。可能人们认为调参不会很难,这也使得研究一种合理的初始化方法一直是一个活跃的研究领域,这里给大家提供一些论文,大量的论文介绍不同的初始化方法。它们没有一个标准的初始化公式,使用何种初始化也是数据驱动的。
