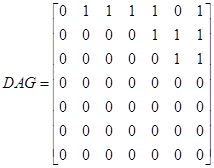贝叶斯网络结构学习若干问题解释
题目:贝叶斯网络结构学习若干问题解释
本篇主要为后续讲解具体结构学习算法打基础,共解释以下几个问题:
1、用于贝叶斯网络结构学习的数据集如何存储?
2、学得的贝叶斯网络结构如何存储?
3、什么是节点顺序order?
4、什么是节点的最大父母个数max_fan_in?
为了方便说明问题,引用如图所示贝叶斯网络(摘自《吴军.数学之美[M].北京:人民邮电出版社,2012.》):
图中贝叶斯网络共有7个节点,分别是心血管疾病、胆固醇量、血脂、吸烟、运动量、饱和脂肪摄取量、家庭病史,每个节点的可能取值为心血管疾病(有、无)、胆固醇量(高、低)、血脂(高、低)、吸烟(是、否)、运动量(大、小)、饱和脂肪摄取量(多、少)、家庭病史(有、无),这里将取值进行了简化,仅为了说明问题。
从这个贝叶斯网络可以得到的信息是“心血管疾病依赖于胆固醇量、血脂、吸烟、运动量、家庭病史共六个因素”,“胆固醇量依赖于运动量、饱和脂肪摄取量、家庭病史共三个因素”,“血脂依赖于饱和脂肪摄取量、家庭病史共两个因素”,即贝叶斯网络中往往是“果”是“因”的“父母(parents)”,例如家族病史是先天的,肯定是先有家族病史才有的心血管疾病;但也可以反过来说当知道一个人得了心血管疾病时可以推测他有家族病史的概率;当然也可以根据一个人是否有家庭病史去推测其患心血管疾病的概率,这其中就是通过贝叶斯公式相互转换:
有关“因”“果”依赖关系的补充说明@20181211
前一段中提到:贝叶斯网络中往往是“果”是“因”的“父母(parents)”,这有点不符合常理,但在《周志华.机器学习[M]. 北京: 清华大学出版社,2016.》中的图7.1和图7.2中均是“果”是“因”的“父母(parents)”,实际上这并没有错,只是出发点不同而已。从逻辑关系上,“果”依赖于“因”,数据集的特征x为“因”,类别标记y为“果”,机器学习的任务是根据“因”(特征)预测“果”(类别标记),因此判别式模型求解后验概率P(y|x),生成式模型先求联合概率P(x,y)再进一步根据贝叶斯公式得到后验概率P(y|x)=P(x,y)/P(x),即“因”是“果”的“父母(parents)”,注意现在说的是逻辑关系。但具体到贝叶斯分类器,例如最简单的朴素贝叶斯分类器,对于此类生成式模型,我们求解联合概率P(x, y),而P(x, y)=P(y)P(x|y),朴素贝叶斯分类器“朴素”之处在于求解似然概率P(x|y)时假设各属性相互独立,注意到似然概率P(x|y)中特征x(因)依赖于类别标记y(果),因此才有了《周志华.机器学习[M]. 北京: 清华大学出版社,2016.》图7.1(a)中的所有属性x均依赖于类别标记y,似乎是“因”(特征)依赖于“因”(类别标记),贝叶斯网情况类似。其实造成这一现象的主要原因在于将求解后验概率转化为求解似然概率,因为后验概率无法估计,而似然概率可以估计(参见西瓜书7.3节的朴素贝叶斯分类器)。到此补充结束,以下为原文:
将贝叶斯公式中的A和B赋予实际含义即可,如A为心血管疾病、B为血脂。根据已知结果去得到未知的事件的概率称为贝叶斯网络推断(Inference),很多时候不能做精确推断,因为“精确推断”已被证明是NP-hard的(简单但不严谨的来说就是在有生之年不能得到计算结果),因此经常采用Gibbs采样等近似推断方法,详见《周志华.机器学习[M]. 北京: 清华大学出版社,2016.》的第7.5.3节。
图中仅描述了贝叶斯网络的结构信息,另外还需要贝叶斯网络的参数信息;例如有心血管疾病且血脂高的概率、有心血管疾病且血脂低的概率、无心血管疾病且血脂高的概率、无心血管疾病且血脂低的概率,此四个概率值描述了从节点心血管疾病到血脂那条有向边的依赖关系(节点血脂的依赖关系),可表达如下(即条件概率P(血脂|心血管疾病)):
|
|
血脂低 |
血脂高 |
| 有心血管疾病 |
0.3 |
0.7 |
| 无心血管疾病 |
0.8 |
0.2 |
此表即为条件概率表(Conditional Probability Table, CPT)。
以上是一种简单的情况,例如要列出节点家族病史的依赖关系,可以表达如下(即条件概率P(家族病史|心血管疾病, 胆固醇量, 血脂)):
|
|
无家族病史 |
有家族病史 |
| 无心血管疾病、胆固醇量低、血脂低 |
0.9 |
0.1 |
| 无心血管疾病、胆固醇量低、血脂高 |
0.6 |
0.4 |
| 无心血管疾病、胆固醇量高、血脂低 |
0.7 |
0.3 |
| 无心血管疾病、胆固醇量高、血脂高 |
0.5 |
0.5 |
| 有心血管疾病、胆固醇量低、血脂低 |
0.4 |
0.6 |
| 有心血管疾病、胆固醇量低、血脂高 |
0.2 |
0.8 |
| 有心血管疾病、胆固醇量高、血脂低 |
0.3 |
0.7 |
| 有心血管疾病、胆固醇量高、血脂高 |
0.1 |
0.9 |
有了以上关于贝叶斯网络的简单基础,下面回答开篇的两个问题,注意此时是准备学习贝叶斯网络结构,即结构是未知的:
1、用于贝叶斯网络结构学习的数据集如何存储?
仍以开篇的贝叶斯网络为例(记住,此时结构是未知的),此时仅知道要学得的贝叶斯网络共有7个节点,分别是心血管疾病、胆固醇量、血脂、吸烟、运动量、饱和脂肪摄取量、家庭病史,我们要从经验数据中学得这7个节点的依赖关系,那么数据集是什么样子呢?
| 心血管疾病 |
有 |
无 |
有 |
有 |
无 |
无 |
无 |
有 |
…… |
| 胆固醇量 |
高 |
低 |
高 |
高 |
低 |
高 |
高 |
低 |
…… |
| 血脂 |
高 |
高 |
低 |
高 |
高 |
高 |
低 |
低 |
…… |
| 吸烟 |
是 |
否 |
是 |
是 |
是 |
否 |
否 |
否 |
…… |
| 运动量 |
小 |
小 |
小 |
大 |
大 |
大 |
小 |
小 |
…… |
| 饱和脂肪摄取量 |
多 |
少 |
多 |
多 |
多 |
少 |
少 |
少 |
…… |
| 家庭病史 |
无 |
无 |
有 |
无 |
无 |
有 |
无 |
无 |
…… |
如表所示,数据一般就是如此存储的,每一列代表一个案例(case),每一行代表某个节点的取值,数据集存成一个矩阵,大小为n*m,n为节点(node)个数,m为案例个数。这里面还有一个参数是贝叶斯网络结构学习算法经常需要的,那就是每一个节点可能的取值个数node_sizes(the number of values each node can take on),比如本例中,七个节点的可能取值个数均为两种,因此node_sizes=[2,2,2,2,2,2,2];;当然,若将胆固醇量分为高、中、低三档,运动量分为大、中、小三档,则node_sizes=[2,3,2,2,3,2,2]; 。一般来说,每个节点的取值均为离散的,比如本例的每个节点只有简单有“有/无”、“高/低”、“是/否”、“大/小”、“多/少”等,如果将血脂具体为医学上测得的数值而非例子中简单的“高/低”,此节点将成为连续的,在学习贝叶斯网络结构时要特殊处理,此处不再多述。
2、学得的贝叶斯网络结构如何存储?
有了数据集,将数据集作为输入变量丢给贝叶斯网络结构学习函数,得到一个贝叶斯网络结构,这个结构是什么样子呢?
当然,这个结构不会如本篇开头的贝叶斯网络结构图,那只是一种可视化结果而已,为了让人获得直观的视觉效果。实际中学得的贝叶斯网络结构是用矩阵存储的,例如开篇例子的网络结构一般表示如下:
矩阵第1行到第7行分别代表心血管疾病、胆固醇量、血脂、吸烟、运动量、饱和脂肪摄取量、家庭病史,第1列到第7列含义也是如此。对比矩阵和贝叶斯网络结构图可以看出,DAG(i,j)=1表示第i个节点是第j个节点的父母,其中DAG(i,j)表示矩阵的第i行第j个元素。
3、什么是节点顺序order?
对于有些贝叶斯网络结构学习算法(比如著名的K2算法),往往会要求输入节点顺序,即可以将先验知识(或专家知识)融入到结构学习过程中。
以例子来说明,根据我们的经验,可以将这7个节点顺序确定为【心血管疾病、胆固醇量、血脂、吸烟、运动量、饱和脂肪摄取量、家庭病史】,节点顺序确定后,排在前面的可能是后面节点的父母,当然也可能不是;但后面的节点肯定不是前面节点的父母,例如从学得的结果可以看出,吸烟根本不是运动量、饱和脂肪摄取量、家庭病史三个节点的父母,即使它排在三者之前。后面会具体聊到K2算法,从该算法的流程可以看出,算法内部求最优评分时只会遍历检查在当前节点的节点顺序之前的各节点是否为其父母。然而,并不是任何时候都有先验知识,当无法确定节点顺序时则需要使用不需输入节点顺序的结构学习算法。
4、什么是节点的最大父母个数max_fan_in?
大部分函数会要求输入每个节点的最大父母个数,即the largest number of parents we allow per node,当然这个参数一般默认为节点个数(或节点个数减1)。从字面意思理解也很容易,就是一个节点能同时拥有的父母个数,比如上例中,家族病史有三个父母,运动量、饱和脂肪摄取量分别有两个父母,胆固醇量、血脂、吸烟分别有一个父母,若依次设置心血管疾病、胆固醇量、血脂、吸烟、运动量、饱和脂肪摄取量、家庭病史的最大父母个数为max_fan_in=[2,2,2,2,2,2,2],即每个节点均最多有两个父母,则对于家庭病史这个节点来说必须从其三个父母中舍掉一个,当然这个过程在算法内部的学习过程中已经直接做好了。