R做线性回归及检验

使用R对内置鸢尾花数据集iris（在R提示符下输入iris回车可看到内容）进行回归分析，自行选择因变量和自变量，注意Species这个分类变量的处理方法

## 将iris数据加载进来
attach(iris)
## 查看iris数据的整体情况
str(iris)
## 'data.frame':    150 obs. of  5 variables:
##  $ Sepal.Length: num  5.1 4.9 4.7 4.6 5 5.4 4.6 5 4.4 4.9 ...
##  $ Sepal.Width : num  3.5 3 3.2 3.1 3.6 3.9 3.4 3.4 2.9 3.1 ...
##  $ Petal.Length: num  1.4 1.4 1.3 1.5 1.4 1.7 1.4 1.5 1.4 1.5 ...
##  $ Petal.Width : num  0.2 0.2 0.2 0.2 0.2 0.4 0.3 0.2 0.2 0.1 ...
##  $ Species     : Factor w/ 3 levels "setosa","versicolor",..: 1 1 1 1 1 1 1 1 1 1 ...
可以看出，共有150个样本，5个变量，前四个是数值型，第五个变量是因子型。
## 查看数据散点分布情况
pairs(iris[, 1:4], col = "blue")

从上图可以看出，Sepal.Length与Petal.Length、Petal.Length与Petal.Width存在明显的正相关性。接下来选择这两对变量分别建立回归模型。

(lm1 <- lm(Sepal.Length ~ Petal.Length))
## 
## Call:
## lm(formula = Sepal.Length ~ Petal.Length)
## 
## Coefficients:
##  (Intercept)  Petal.Length  
##        4.307         0.409
(lm2 <- lm(Petal.Length ~ Petal.Width))
## 
## Call:
## lm(formula = Petal.Length ~ Petal.Width)
## 
## Coefficients:
## (Intercept)  Petal.Width  
##        1.08         2.23
summary(lm1)
## 
## Call:
## lm(formula = Sepal.Length ~ Petal.Length)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -1.2468 -0.2966 -0.0152  0.2768  1.0027 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept)    4.3066     0.0784    54.9   <2e-16 ***
## Petal.Length   0.4089     0.0189    21.6   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.407 on 148 degrees of freedom
## Multiple R-squared:  0.76,   Adjusted R-squared:  0.758 
## F-statistic:  469 on 1 and 148 DF,  p-value: <2e-16
summary(lm2)
## 
## Call:
## lm(formula = Petal.Length ~ Petal.Width)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -1.3354 -0.3035 -0.0295  0.2578  1.3945 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   1.0836     0.0730    14.8   <2e-16 ***
## Petal.Width   2.2299     0.0514    43.4   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.478 on 148 degrees of freedom
## Multiple R-squared:  0.927,  Adjusted R-squared:  0.927 
## F-statistic: 1.88e+03 on 1 and 148 DF,  p-value: <2e-16
两个模型的拟合效果都不错，但从R平方和角度考虑，lm2的模型效果好点。


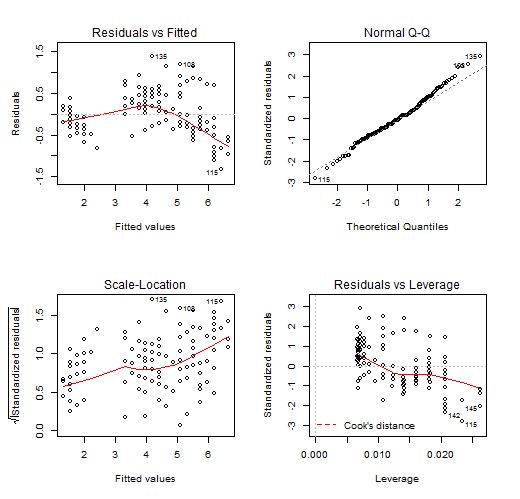
##对建立的模型分别进行残差检验
par(mfrow = c(2, 2))
plot(lm1)

plot(lm2)

par(mfrow = c(1, 2))
plot(Petal.Length, Sepal.Length)
lines(Petal.Length, lm1$fitted.values)
plot(Petal.Width, Petal.Length)
lines(Petal.Width, lm2$fitted.values)

数据中的第五个变量Species是因子型变量，在进行回归建模前，需要对其进行哑变量处理，提高模型精确度。在R建立回归模型时，会主动对因子型变量进行哑变量处理，下面先利用Sepal.Width、Species对Sepal.Length建立回归模型，看看效果。

lm3 <- lm(Sepal.Length ~ Sepal.Width + Species)
summary(lm3)
## 
## Call:
## lm(formula = Sepal.Length ~ Sepal.Width + Species)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -1.3071 -0.2571 -0.0533  0.1954  1.4125 
## 
## Coefficients:
##                   Estimate Std. Error t value Pr(>|t|)    
## (Intercept)          2.251      0.370    6.09  9.6e-09 ***
## Sepal.Width          0.804      0.106    7.56  4.2e-12 ***
## Speciesversicolor    1.459      0.112   13.01  < 2e-16 ***
## Speciesvirginica     1.947      0.100   19.47  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.438 on 146 degrees of freedom
## Multiple R-squared:  0.726,  Adjusted R-squared:  0.72 
## F-statistic:  129 on 3 and 146 DF,  p-value: <2e-16
par(mfrow = c(2, 2))
plot(lm3)

从建立的模型的各系数的p值看出，各参量均是显著的。R平方和也有0.726，处于一个相对合理的水平。故该模型是可以接受的。

2 使用R对内置longley数据集进行回归分析，如果以GNP.deflator作为因变量y，问这个数据集是否存在多重共线性问题？应该选择哪些变量参与回归？

答：

## 查看longley的数据结构
str(longley)
## 'data.frame':    16 obs. of  7 variables:
##  $ GNP.deflator: num  83 88.5 88.2 89.5 96.2 ...
##  $ GNP         : num  234 259 258 285 329 ...
##  $ Unemployed  : num  236 232 368 335 210 ...
##  $ Armed.Forces: num  159 146 162 165 310 ...
##  $ Population  : num  108 109 110 111 112 ...
##  $ Year        : int  1947 1948 1949 1950 1951 1952 1953 1954 1955 1956 ...
##  $ Employed    : num  60.3 61.1 60.2 61.2 63.2 ...
longly数据集中有7个变量16个观测值，7个变量均属于数值型。

首先建立全量回归模型
lm1 <- lm(GNP.deflator ~ ., data = longley)
summary(lm1)
## 
## Call:
## lm(formula = GNP.deflator ~ ., data = longley)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -2.009 -0.515  0.113  0.423  1.550 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)  
## (Intercept)  2946.8564  5647.9766    0.52    0.614  
## GNP             0.2635     0.1082    2.44    0.038 *
## Unemployed      0.0365     0.0302    1.21    0.258  
## Armed.Forces    0.0112     0.0155    0.72    0.488  
## Population     -1.7370     0.6738   -2.58    0.030 *
## Year           -1.4188     2.9446   -0.48    0.641  
## Employed        0.2313     1.3039    0.18    0.863  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.19 on 9 degrees of freedom
## Multiple R-squared:  0.993,  Adjusted R-squared:  0.988 
## F-statistic:  203 on 6 and 9 DF,  p-value: 4.43e-09
建立的模型结果是令人沮丧的，6个变量的显著性p值只有两个有一颗星，说明有些变量不适合用于建模。

看各自变量是否存在共线性问题。此处利用方差膨胀因子进行判断：方差膨胀因子VIF是指回归系数的估计量由于自变量共线性使得方差增加的一个相对度量。一般建议，如VIF>10，表明模型中有很强的共线性问题。
library(car)
vif(lm1, digits = 3)
##          GNP   Unemployed Armed.Forces   Population         Year 
##      1214.57        83.96        12.16       230.91      2065.73 
##     Employed 
##       220.42
从结果看，所有自变量的vif值均超过了10，其中GNP、Year更是高达四位数，存在严重的多种共线性。接下来，利用cor（）函数查看各自变量间的相关系数。
plot(longley[, 2:7])

cor(longley[, 2:7])
##                 GNP Unemployed Armed.Forces Population   Year Employed
## GNP          1.0000     0.6043       0.4464     0.9911 0.9953   0.9836
## Unemployed   0.6043     1.0000      -0.1774     0.6866 0.6683   0.5025
## Armed.Forces 0.4464    -0.1774       1.0000     0.3644 0.4172   0.4573
## Population   0.9911     0.6866       0.3644     1.0000 0.9940   0.9604
## Year         0.9953     0.6683       0.4172     0.9940 1.0000   0.9713
## Employed     0.9836     0.5025       0.4573     0.9604 0.9713   1.0000
从散点分布图和相关系数，均可以得知，自变量间存在严重共线性。


接下来利用step（）函数进行变量的初步筛选。


lm1.step <- step(lm1, direction = "backward")
## Start:  AIC=10.48
## GNP.deflator ~ GNP + Unemployed + Armed.Forces + Population + 
##     Year + Employed
## 
##                Df Sum of Sq  RSS   AIC
## - Employed      1      0.04 12.9  8.54
## - Year          1      0.33 13.2  8.89
## - Armed.Forces  1      0.74 13.6  9.39
##                     12.8 10.48
## - Unemployed    1      2.08 14.9 10.88
## - GNP           1      8.47 21.3 16.59
## - Population    1      9.48 22.3 17.33
## 
## Step:  AIC=8.54
## GNP.deflator ~ GNP + Unemployed + Armed.Forces + Population + 
##     Year
## 
##                Df Sum of Sq  RSS   AIC
## - Year          1      0.46 13.3  7.11
##                     12.9  8.54
## - Armed.Forces  1      1.79 14.7  8.62
## - Unemployed    1      5.74 18.6 12.43
## - GNP           1      9.40 22.3 15.30
## - Population    1      9.90 22.8 15.66
## 
## Step:  AIC=7.11
## GNP.deflator ~ GNP + Unemployed + Armed.Forces + Population
## 
##                Df Sum of Sq  RSS   AIC
## - Armed.Forces  1       1.3 14.7  6.62
##                     13.4  7.11
## - Population    1       9.7 23.0 13.82
## - Unemployed    1      14.5 27.8 16.86
## - GNP           1      35.2 48.6 25.76
## 
## Step:  AIC=6.62
## GNP.deflator ~ GNP + Unemployed + Population
## 
##              Df Sum of Sq  RSS   AIC
##                   14.7  6.62
## - Unemployed  1      13.3 28.0 14.95
## - Population  1      13.3 28.0 14.95
## - GNP         1      48.6 63.2 27.99
根据AIC 赤池信息准则，模型最后选择Unemployed、Population、GNP三个因变量参与建模。
查看进行逐步回归后的模型效果
summary(lm1.step)
## 
## Call:
## lm(formula = GNP.deflator ~ GNP + Unemployed + Population, data = longley)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -2.047 -0.682  0.196  0.696  1.435 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 221.12959   48.97251    4.52  0.00071 ***
## GNP           0.22010    0.03493    6.30  3.9e-05 ***
## Unemployed    0.02246    0.00681    3.30  0.00634 ** 
## Population   -1.80501    0.54692   -3.30  0.00634 ** 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.11 on 12 degrees of freedom
## Multiple R-squared:  0.992,  Adjusted R-squared:  0.989 
## F-statistic:  472 on 3 and 12 DF,  p-value: 1.03e-12
从各判定指标可以看出，模型的结果是可喜的。参与建模的三个变量和截距均是显著的。R平方和也高达0.992。