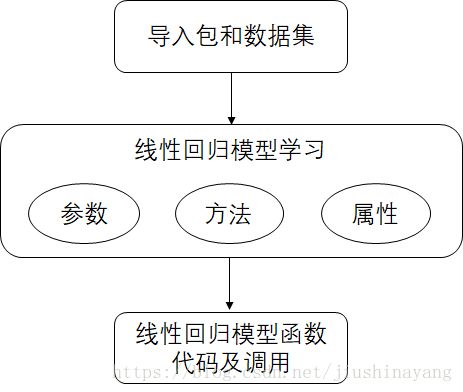
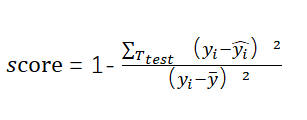学习笔记二_线性回归模型python实战——《python大战机器学习》

线性回归模型的python实战如下：

                                                     

1. 导入包和数据集

# 导入包
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets, linear_model, discriminant_analysis, model_selection
# 在书中，从sklearn中导入的最后一个模块为cross_validation而不是model_selection，但cross_validaton在0.18版本中被弃用，其中内容移至model_selection中。
# 在线性回归问题中，使用的数据集是scikit-learn自带的一个糖尿病病人的数据集。
 


# 加载数据集的函数如下：
def load_data():
    diabetes = datasets.load_diabetes()  # diabete指糖尿病
    return model_selection.train_test_split(diabetes.data, diabetes.target, test_size=0.25, random_state=0)
# 返回值为：一个元组，元组依次是：训练样本集、测试样本集、训练样本集对应的标签值、测试样本集对应的标签值。
# load_data()函数加载数据集并随机切分数据集为两个部分，其中test_size指定了测试集为原始数据集的大小（比例）。

 

2. 线性回归模型

LinearRegression是scikit-learn提供的线性回归模型，它的原型为：

class sklearn.linear_model.LinearRegression(fit_intercept=True, normalize=False, copy_x=True, n_jobs=1)

---

参数：

fit_intercept：一个布尔值，指定是否需要计算b值。如果为False，那么不计算b值。

normalize: 一个布尔值。如果为True,那么训练样本在回归之前会被归一化。

copy_x: 一个布尔值。如果为True，则会复制X。

n_jobs: 一个正数。任务并行时指定的CPU数量。如果为-1，则使用所有可用的CPU。

---

属性：

coef_: 权重向量。

intercept_: b值。

---

方法：

fit(X, y[ ,sample_weight]): 训练模型。

predict(X): 用模型进行预测，返回预测值。

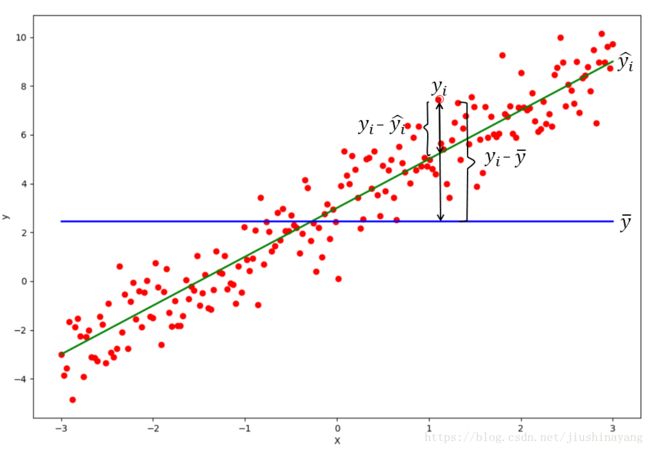
score(X, y[ ,sample_weight]): 返回预测性能得分。设预测集为，真实值为，真实值的均值为，预测值为，则：

，定义与判定系数R²相同。

score不超过1，但是可能为负值（预测效果太差）；score越大，预测性能越好。

             

 

3. 使用LinearRegression的函数及调用如下：

# 使用LinearRegression的函数如下：
def test_LinearRegression(*data):  # 在参数名之前使用一个星号*，可以让函数接受任意多的位置参数。
    x_train, x_test, y_train, y_test = data
    regr = linear_model.LinearRegression()
    regr.fit(x_train, y_train)
    print('Coefficients:%s, intercept:%.2f' % (regr.coef_, regr.intercept_))
    # https://blog.csdn.net/qq_37482544/article/details/63720726. %格式符是为真实值预留位置，并控制显示的格式。
    # %s:采用字符串显示；%.2f表示小数点后面精确到2位的浮点数。
    print("Residual sum of squares:%.2f"%np.mean((regr.predict(x_test) -y_test )**2))
    # Residual sum of squares指残差平方和，预测值与实际值之差的平方和；**是幂运算。
    print('Score:%.2f'%regr.score(x_test, y_test))
    # data依次指定了训练样本集、测试样本集、训练样本集对应的标签值、测试样本集对应的标签值。
    # 该函数简单从训练数据集中学习，然后从测试数据集中预测。


# 函数调用
x_train, x_test, y_train, y_test = load_data()
test_LinearRegression(x_train, x_test, y_train, y_test)

 
# 函数调用结果
# Coefficients:[ -43.26774487 -208.67053951  593.39797213  302.89814903 -560.27689824，
# 261.47657106   -8.83343952  135.93715156  703.22658427   28.34844354], 
# intercept:153.07
# Residual sum of squares:3180.20
# Score:0.36